地震數據譜反演壓縮感知算法實現及應用

夏紅敏 劉蘭鋒 張顯輝 陳雙全*

(①中國石化石油勘探開發研究院，北京100083；②中國石油大學(北京)油氣資源與探測國家重點實驗室，北京102249；③中國石油大學(北京)CNPC物探重點實驗室，北京102249)

0 引言

為了解決油氣勘探中薄儲層的識別問題，地球物理學家們嘗試了許多提高地震資料分辨率的處理方法。Portniaguine等[1-2]和Chopra等[3-5]最早基于地層反射系數奇、偶分解原理提出了譜反演方法；Puryear等[6]將反射系數對分解成奇、偶兩個分量，根據奇、偶分量對薄層的分辨能力不同，首先構建了地震數據譜反演方法模型，合成數據測試和實際地震數據反演驗證了方法的正確性，為提高地震數據分辨率提供了一種新方法。在隨后的幾年，譜反演方法得到了快速的發展和完善[7-8]。

Zhang等[9]介紹了一種反射系數基追蹤反演方法，該方法通過建立反映反射模式的函數字典，將地震道數據看成是這些函數的疊加，并在反演過程中引入先驗信息進行反演約束。柴新濤等[10]提出基于最小二乘奇異值分解(LSQR)算法與模擬退火算法相結合的方法，完成了稀疏譜與非稀疏譜兩種假設條件下的反演，同時分析了譜反演結果的影響因素。Yuan等[11]將反射系數反演與稀疏貝葉斯學習相結合實現了譜反演，通過添加、刪除或重新估計等方式檢索稀疏反射系數序列，無需預先設置非零反射系數的個數，并在合成數據、物理模型數據和實際數據中驗證了該方法，結果表明譜反演方法能較好地識別地下薄層。劉萬金等[12]利用譜反演法有效地提高了地震數據的分辨率，并將其應用于地震屬性分析。田立新等[13]基于貝葉斯理論框架，將測井等信息轉換為地質統計先驗信息，引入到譜反演過程，提出地質統計學譜反演法。張華等[14]及劉潔等[15]在實際地震資料處理中應用譜反演，均取得不錯的效果。張軍華等[16]實現了基于Moore-Penrose算法的譜反演；陳祖慶等[17]實現了基于壓縮感知的譜反演算法。

地震數據譜反演的假設條件是反射系數為稀疏序列，而稀疏性也是信號分析中壓縮感知算法的條件之一。因此，將壓縮感知算法引入地震數據譜反演，可以很好地實現地震數據譜反演方法的求解。另外，針對實際地震數據反演過程中地震子波譜難以估算的問題，唐文博等[18]提出利用地震數據二次譜估算子波譜的方法，直接將頻率域的地震子波譜用于譜反演。

本文提出聯合地震數據二次譜計算方法及基于壓縮感知算法的譜反演方法，試算結果表明，可以很好地解決實際數據譜反演中的穩定性問題。

1 方法原理

1.1 譜反演方法

在地震數據時間域，利用脈沖函數的性質，將時間間隔為T的地層頂、底反射系數對(r1，r2)表示為[7]

g(t)=r1δ(t-t1)+r2δ(t-t1-T)

(1)

式中：r1、r2分別是地層頂、底界面的反射系數；t為時間序列采樣；t1、t2分別是頂、底界面的反射時間，T=t2-t1；δ(·)為脈沖函數。如果零時間設置到地層中點，則有

(2)

對式(2)進行傅里葉變換得到

(3)

根據反射系數對的奇偶分解原理[6]可得

g(t,f)=2recos(πfT)+j2rosin(πfT)

(4)

其中re、ro為地層反射系數對(r1，r2)的偶分量和奇分量，且2re=r1+r2，2ro=r1-r2。

頻率域反射系數對的實部Re[·]和虛部Im[·]為

Re[g(t,f)]=2recos(πfT)

(5)

Im[g(t,f)]=2rosin(πfT)

(6)

則單一層的頂、底反射系數對 Δt=t1+T/2的時延譜為

米多想到自己莫名丟失的錄音筆，正想問鮑澤，對方卻神色一變，突然擺出一副不耐煩的樣子。隨即，米多的耳旁傳來了一個熟悉的聲音。

Re[e-j2πfΔtg(t,f)]=2recos(πfT)cos(2πfΔt)+

2rosin(πfT)sin(2πfΔt)

(7)

Im[e-j2πfΔtg(t,f)]=2rosin(πfT)cos(2πfΔt)-

2recos(πfT)sin(2πfΔt)

(8)

根據以上推導可得到N個稀疏反射系數序列r(ti)，i=1，2，…，N，其頻率域反射系數的奇、偶分量形式如下

2ro(i，i+1)sin(πfTi)sin(2πfΔti)]

(9)

2re(i，i+1)cos(πfTi)sin(2πfΔti)]

(10)

式中：2re(i，i+1)=ri+ri+1；2ro(i，i+1)=ri-ri+1。

式(9)和式(10)表明，可以利用地震記錄和地震子波的部分譜信息進行反演進而得到反射系數序列，該方法即地震數據譜反演[7]。因此，目標函數式為

(11)

譜反演目標函數求解過程是利用部分地震信息求解整個時間域內稀疏反射系數的過程，壓縮感知的基本思想是在滿足有效等距條件(RIP)下，利用少量采樣信號重構出完整的原信號。二者思路不謀而合，因此本文選用壓縮感知算法解決譜反演問題。假設反射系數為稀疏信號，可將譜反演目標函數重寫為最優化目標函數公式

(12)

式中：r是待求解的反射系數；b是地震記錄頻譜與地震子波頻譜之比；A是構建的測量矩陣；τ表示反射系數的最大幅值，一般取0.2。

可將式(12)的約束優化條件改寫為無約束優化條件

(13)

其中λ是用于平衡二次項和稀疏項結果權重的正則化參數。上述最優化過程為帶邊界約束的二次規劃問題，正則化參數用于控制稀疏解。為了將非凸優化問題轉化為凸優化問題，采用梯度投影稀疏重構(Gradient Projection for Sparse Reconstruction， GPSR)算法[19]進行求解。

1.2 地震子波譜的求取

式(11)表明，地震數據譜反演目標函數與地震子波譜相關。因此，地震子波譜估算的準確度直接影響譜反演結果的準確性。本文通過地震數據二次譜求取地震子波譜，具體方法如下。

首先，根據地震數據褶積模型，得到頻率域的地震數據振幅譜關系式

AS(f)=AW(f)Ar(f)

(14)

式中AS(f)、AW(f)和Ar(f)分別為地震記錄、地震子波和反射系數的振幅譜。

然后，設法提取地震子波振幅譜。在頻率域，地震信號中同時包含反射系數與地震子波的頻譜信息，無法將其有效分離。而在譜模擬假設條件下，地震子波的振幅譜主要為地震記錄頻譜中光滑的低頻分量，因此，對式(14)兩邊同時進行傅里葉變換，可得到地震數據的二次譜，即地震子波二次譜與反射系數二次譜的褶積，表達式為

(15)

2 合成數據測試

進行合成數據測試時，首先利用合成地震道數據驗證由地震記錄二次譜求取地震子波譜方法的準確性。圖1顯示了30Hz Ricker子波和三種不同信噪比的合成地震記錄的二次譜曲線，可以看出：在0～45Hz頻率范圍內，合成地震記錄的二次譜可以很好地模擬地震子波的振幅譜。圖2顯示合成地震記錄振幅譜(黑線)、利用二次譜得到的子波譜(紅線)和已知的地震子波譜(藍線)。對比表明，利用地震記錄二次譜可以計算得到最吻合的地震子波頻譜，為實際地震數據譜反演中的地震子波譜估算提供了實用且有效的方法。

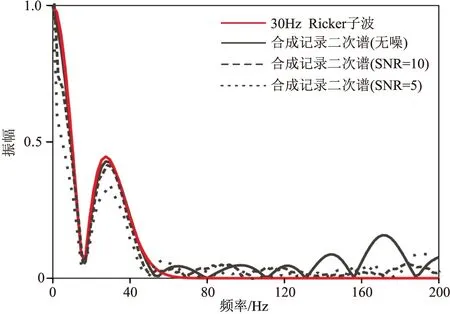
圖1 地震子波與合成地震記錄二次譜對比

利用地震記錄二次譜估算得到較準確的地震子波譜后，通過GPSR算法對合成地震記錄進行譜反演試算。圖3分別展示了30Hz地震Ricker子波(圖3a)、無噪聲的合成地震記錄(圖3b)以及信噪比SNR分別為10、5、2的合成地震記錄(圖3c～圖3e)。譜反演結果如圖4所示。對比表明，對于信噪比較高的地震數據，通過譜反演可以得到準確的反射系數。但是當SNR < 5時，反演結果受信噪比影響較大，低信噪比(如SNR=2)地震數據反演結果與實際反射系數的偏差較大。因此，譜反演輸入地震數據的信噪比不能太低。

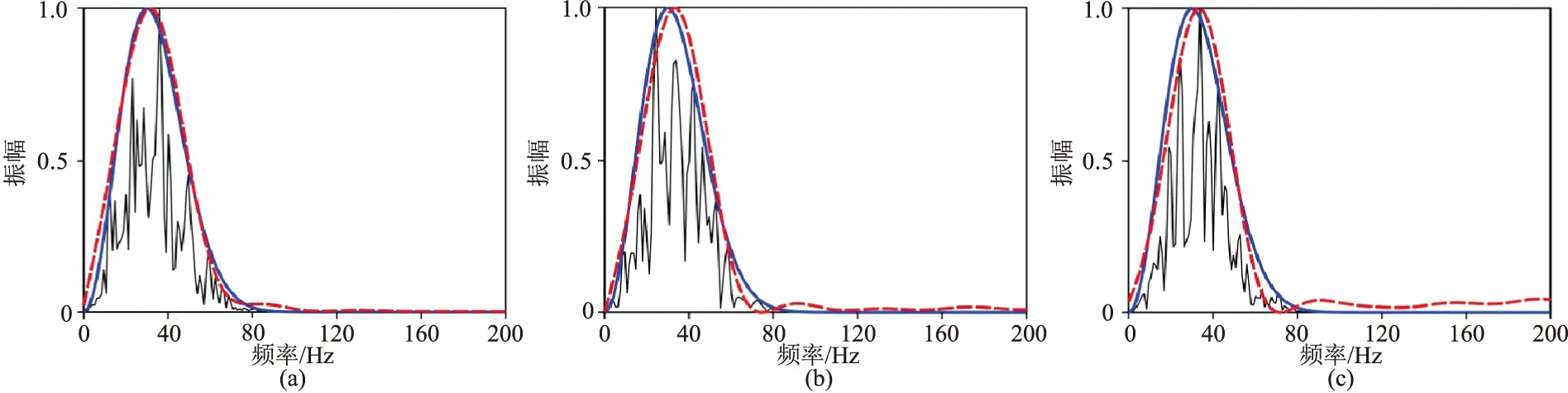
圖2 合成地震記錄振幅譜(黑線)、地震子波振幅譜(藍線)和計算得到的地震子波振幅譜(紅線)對比(a)無噪聲； (b)SNR=10； (c)SNR=5

圖3 地震子波及合成地震記錄對比(a)Ricker子波； (b)無噪； (c)SNR=10； (d)SNR=5； (e)SNR=2

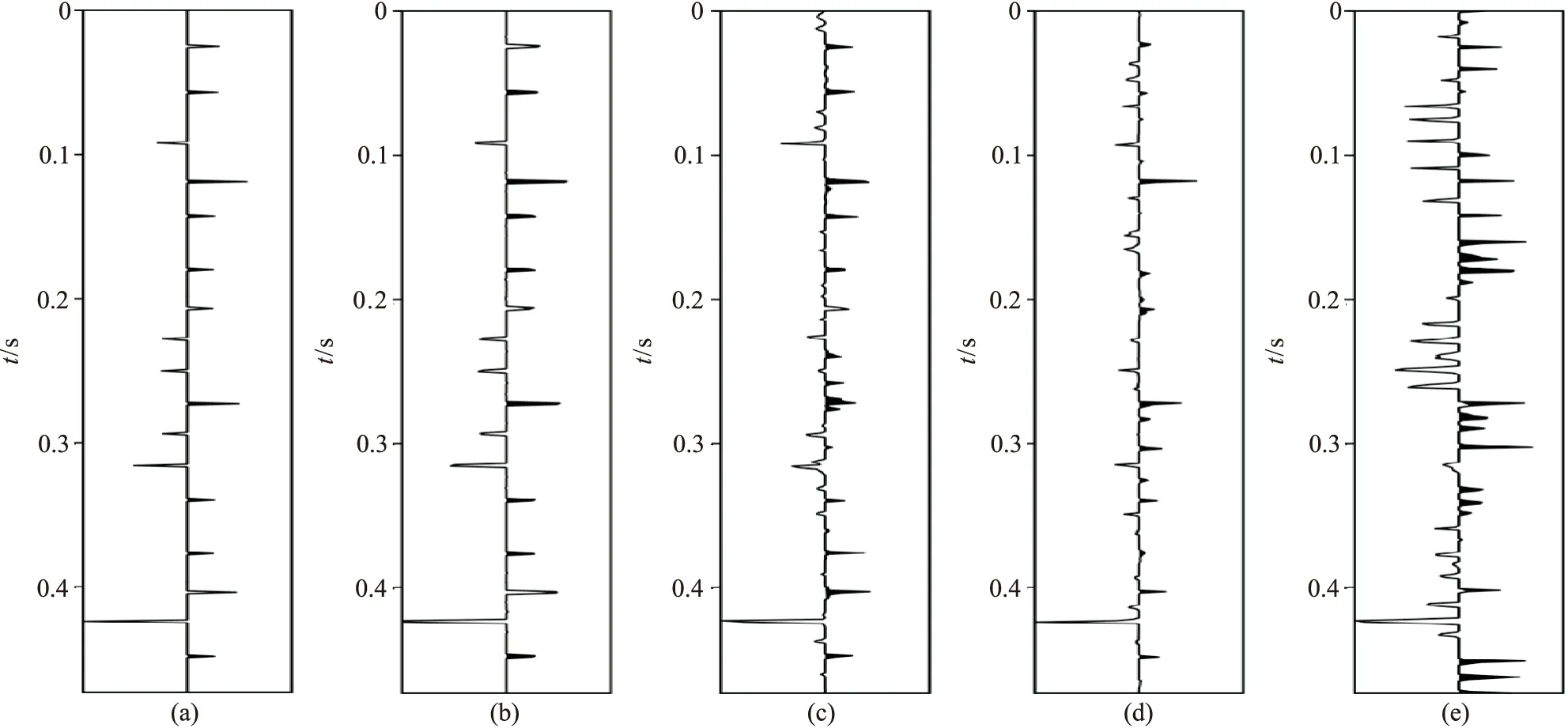
圖4 原始反射系數與譜反演結果對比(a)原始反射系數序列； (b)無噪； (c)SNR=10； (d)SNR=5； (e)SNR=2

3 實際數據應用

地震數據譜反演最終得到的是反射系數序列，之后，可以進一步反演波阻抗，也可以將反射系數與寬頻地震子波合成高分辨率地震記錄。本文利用基于壓縮感知算法的譜反演結果進行實際地震數據提高分辨率處理的應用，以驗證該反演算法的穩定性和有效性。處理流程包括：

(1)對地震數據進行頻譜分析，確定反演的頻率范圍；

(2)計算地震記錄的二次譜，進行低通濾波處理；

(3)求取地震子波譜；

(4)利用式(11)求解反射系數序列；

(5)利用寬頻帶子波合成地震數據，得到提高分辨率后的處理結果。

所選實際地震工區的目的層為奧陶系風化殼氣藏儲層，由于受上覆煤層影響，目的層的地震資料分辨率較低，后續進行高精度儲層預測難度很大。圖5為工區內一條地震剖面，圖中的強反射同相軸為煤層反射信號。

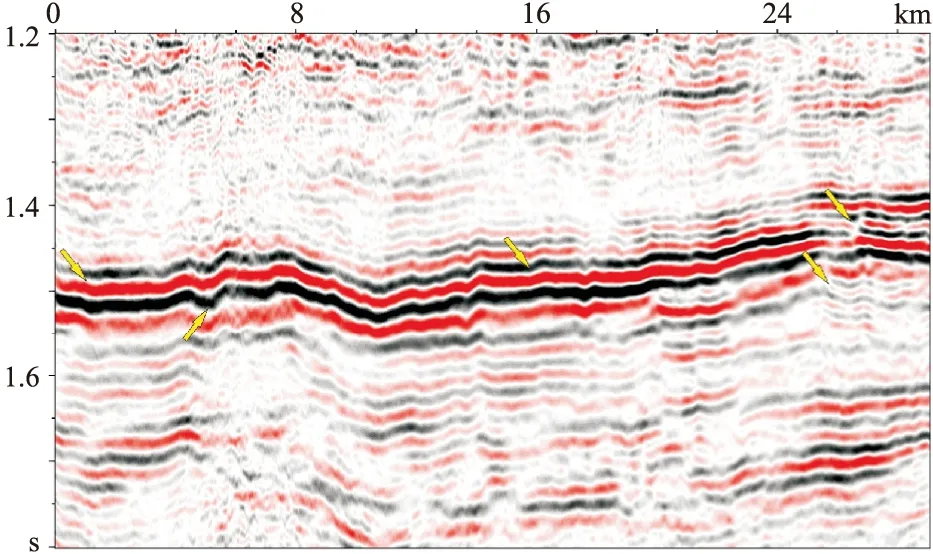
圖5 實際地震數據剖面

根據上述處理流程，首先通過地震數據頻譜分析選取合適的反演頻率范圍，結合反演測試，最終選取的頻率范圍為10～70Hz。其次，利用地震資料的二次譜進行地震子波譜估計。針對該實際數據，采用多道平均譜估算地震子波譜。圖6為地震數據的二次譜(藍色)與低通濾波后的二次譜(紅色)對比，圖7為計算得到的地震子波譜。利用本文提出的譜反演方法對地震數據進行反演，并將反演得到的反射系數序列與寬頻子波合成，輸出提高分辨率處理后的結果(圖8a)。

為了驗證本文方法針對實際地震數據的處理效果，同時對地震數據進行了譜白化處理，結果如圖8b所示。對比兩種方法處理后的地震剖面可以看到：本文方法處理后的地震數據信噪比更高，剖面信息更加豐富，視分辨率得到明顯提高；而利用譜白化處理得到的地震剖面，分辨率提高不明顯，并且信噪比偏低。

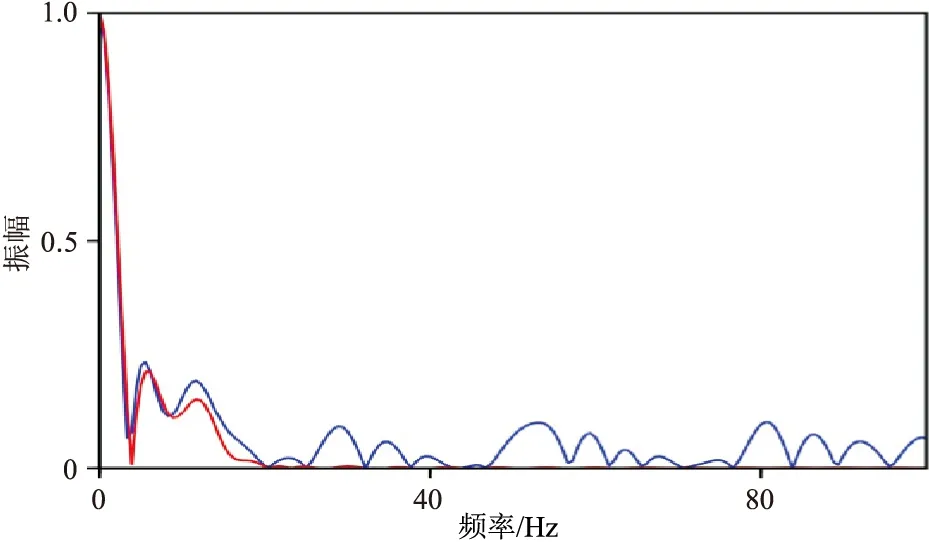
圖6 實際地震數據二次譜(藍色)與濾波后的二次譜(紅色)對比

圖7 計算得到的地震子波振幅譜

圖8 實際數據反演提高分辨率處理(a)及譜白化處理(b)結果對比

對原始地震數據及處理后數據進行分頻掃描，可更好地分析不同方法處理效果。圖9對比了原始數據、譜白化處理及本文方法處理結果的分頻掃描結果，掃描頻率分別為10～40Hz、40～80Hz和80～120Hz。可以看到，在10～40Hz掃描頻段，譜白化處理(圖9d)及本文方法處理(圖9g)結果均能很好地保持原始數據的信息；40～80Hz掃描時譜白化處理結果信噪比明顯降低(圖9e)；在80～120Hz的掃描結果中，原始數據中80Hz以上的信息不足(圖9c)，譜白化處理結果的信噪比更低(圖9f)，只有本文方法處理結果恢復得到了高頻段的有效信號(圖9i)。三個頻段的掃描結果均表明，本文方法處理后的地震剖面的信噪比最高。

圖9 數據分頻掃描剖面對比(a～c)原始數據； (d～f)譜白化處理結果； (g～i)本文方法處理結果

4 結論

本文結合地震記錄的二次譜估算地震子波譜的方法，提出了一種基于壓縮感知算法的地震數據譜反演方法，形成了利用譜反演結果提高地震資料分辨率的數據處理流程。實際地震資料應用結果表明，該處理流程計算步驟和參數選取均較簡單，在實際數據處理中可以很好地恢復高頻段有效信號，而且經過處理后的地震數據信噪比高、橫向連續性好。合成數據測試表明，該方法受原始地震數據信噪比的影響較大，因此對于低信噪比資料的數據反演還需要進一步完善。