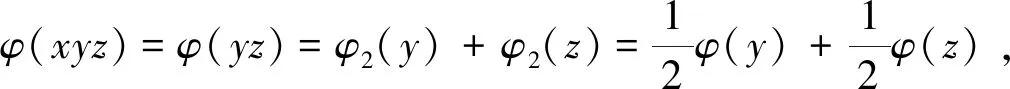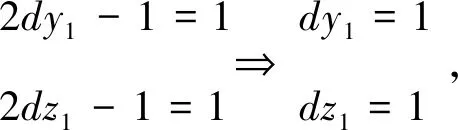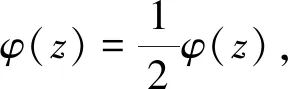三元廣義歐拉函數方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)的解
梁曉艷,高 麗,高 倩
(延安大學 數學與計算機科學學院,陜西 延安 716000)
歐拉函數φ(n)與廣義歐拉函數φ2(n)在數論中都有著重要的作用,近年來,有關歐拉函數的性質以及歐拉方程吸引了很多學者的興趣.在文獻[1-3]中研究了二元歐拉函數方程φ(ab)=k(φ(a))+φ(b))的正整數解.文獻[4]研究了三元歐拉函數方程中φ(xyz)=φ(x)+φ(y)+φ(z)+6的正整數解.文獻[5]研究了四元歐拉方程φ(abcd)=φ(a)+2φ(b)+3φ(c)+4φ(d)的正整數解.文獻[6]研究了包含歐拉函數的方程φ(φ(n))=2w(n)的所有正整數解,文獻[7-8]分別研究了廣義歐拉函數φ2(φ(n))=φ(φ2(n))與φ2(m)=2w(m)3w(m)的正整數解。文獻[9]研究了二元廣義歐拉函數方程φ(ab)=11φ2(a)+13φ2(b)的正整數解.本文通過參閱上述文獻,利用整數的分解以及初等數論的相關知識研究了三元廣義歐拉函數方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)的正整數解.
1 相關引理
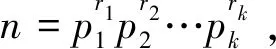
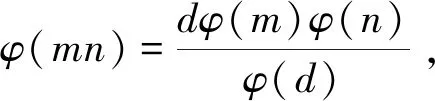
引理3[10]當n≥2時,有φ(n) 定理 三元廣義歐拉函數方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)共有12組正整數解,其解為(x,y,z)=(1,2,3),(2,1,3),(3,1,2),(3,2,1),(1,3,2),(2,3,1),(1,1,2),(1,2,1),(1,2,2)(2,1,1),(2,1,2),(2,2,1). 證明對于三元廣義歐拉函數方程 φ(xyz)=φ2(x)+φ2(y)+φ2(z), (1) 根據x,y,z的不同取值范圍將分為四種情況進行討論. 情況1:當x,y,z中只有一個屬于[1,2]時,假設x=1,2. 即 2φ(yz)=φ(y)+φ(z). (2) 設(y,z)=d,存在正整數y1,z1,使得φ(y)=y1φ(d),φ(z)=z1φ(d),由式(2)可得 從而有 2dy1z1=y1+z1, 分解可得(2dy1-1)(2dz1-1)=1,根據整數的分解可得以下關系式 當d=1時,得y1=1,z1=1,則 φ(y)=1,φ(z)=1,y=z=1,2, 與假設矛盾,所以方程無解. 因為x,y,z的位置是等同的,所以當y=1或z=1時同理可證方程無解. (ii)當x=2時, φ(xyz)=φ(2yz)=1+φ2(y)+φ2(z). 由引理2和引理3得 2φ(2yz)=2+φ(y)+φ(z)≥φ(y)φ(z), φ(y)φ(z)-φ(y)-φ(z)≤2, (φ(y)-1)(φ(z)-1)≤3. ①當(φ(y)-1)(φ(z)-1)<0時,則φ(y)<1或φ(z)<1,由引理3知,方程無解. ②當(φ(y)-1)(φ(z)-1)=0時,則φ(y)=1或φ(z)=1,則y=1,2或z=1,2,因為y,z屬于[3,+∞),所以方程無解. ③當(φ(y)-1)(φ(z)-1)=1時,則有 由引理3知,方程無解. ④當(φ(y)-1)(φ(z)-1)=2時,則有 φ(y)=2,φ(z)=3或φ(y)=3,φ(z)=2. 由引理3知,方程無解. ⑤當(φ(y)-1)(φ(z)-1)=3時,則有 φ(y)=4,φ(z)=2或φ(y)=2,φ(z)=4, 當φ(y)=4,φ(z)=2時, xyz=5,8,10,12,y=5,8,10,12,z=3,4,6,經檢驗,方程無解. 當φ(y)=2,φ(z)=4時, xyz=5,8,10,12,z=5,8,10,12,y=3,4,6,經檢驗,方程無解. 因為x,y,z的位置是等同的,所以當y=1,2或z=1,2時,同理可證方程無解. 情況2:當x,y,z中只有兩個屬于[1,2]時. 假設x,y∈[1,2],則有(x,y)=(1,1)(1,2)(2,1)(2,2)四種情況. (i)當(x,y)=(1,1)時, φ(xyz)=φ(z)=φ2(z), (ii) 當(x,y)=(1,2)時,φ(xyz)=φ(2z)=1+φ2(z),由引理4得 解得φ(z)≤2,即φ(z)=1,2,又因為φ(xyz)為偶數,所以φ(z)=2,z=3,4,6,φ(xyz)=2,xyz=3,4,6,又因為xy=2,所以z=3,所以方程有解(x,y,z)=(1,2,3). (iii)當(x,y)=(2,1)時, φ(xyz)=φ(2z)=1+φ2(z), 由引理4得 解得φ(z)≤2,即φ(z)=1,2. 因為φ(xyz)為偶數,所以φ(z)=2,z=3,4,6,φ(xyz)=2,xyz=3,4,6,又因為xy=2,所以z=3,所以方程有解(x,y,z)=(2,1,3). (vi)當(x,y)=(2,2)時, φ(xyz)=φ(4z)=1+1+φ2(z)=2+φ2(z), 由引理4得 解得φ(z)≤4,即φ(z)=1,2,3,4. 因為φ(xyz)為偶數,所以φ(z)=4,z=5,8,10,12,φ(xyz)=4,xyz=5,8,10,12,又因為xy=4,經檢驗,方程無解. 當x,z∈[1,2]或y,z∈[1,2]時,同理可證方程有解(x,y,z)=(3,1,2),(3,2,1),(1,3,2),(2,3,1). 情況3:當x,y,z都屬于[1,2]時.有(x,y,z)=(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2)八種情況. (i)當(x,y,z)=(1,1,1)時, φ(xyz)=φ(1)=1≠0, 所以(x,y,z)=(1,1,1)不是方程的解. (ii)當(x,y,z)=(1,1,2)時, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(1,1,2)是方程的解. (iii)當(x,y,z)=(1,2,1)時, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(1,2,1)是方程的解. (vi)當(x,y,z)=(1,2,2)時, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(1,2,2)是方程的解. (v)當(x,y,z)=(2,1,1)時, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(2,1,1)是方程的解. (vi)當(x,y,z)=(2,1,2)時, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(2,1,2)是方程的解. (vii)當(x,y,z)=(2,2,1)時, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(2,2,1)是方程的解. (viii)當(x,y,z)=(2,2,2)時, φ(xyz)=φ(8)=4≠φ2(2)+φ2(2)+φ2(2)=3, 所以(x,y,z)=(2,2,2)不是方程的解. 情況4:當x,y,z都屬于[3,+∞)時,由引理2,引理3,引理4得 即 2φ(xyz)=φ(x)+φ(y)+φ(z)≥φ(x)φ(y)φ(z), φ(x)+φ(y)≥(φ(x)φ(y)-1)φ(z), φ(x)+φ(y)≥φ(x)φ(y)-1, 整理得 (φ(x)-1)(φ(y)-1)≤2. 根據φ(x),φ(y)的取值下面分四種情況進行討論. (i) 當(φ(x)-1)(φ(y)-1)<0時,則 φ(x)<1或φ(y)<1, 由引理3知,方程無解. (ii) 當(φ(x)-1)(φ(y)-1)=0時,則 φ(x)=1或φ(y)=1, 則x=1,2或y=1,2,因為x,y,z都屬于[3,+∞);所以方程無解. (iii)當(φ(x)-1)(φ(y)-1)=1時,則有 φ(x)=φ(y)=2,x=y=3,4,6, 經檢驗,方程無解. (iv)當(φ(x)-1)(φ(y)-1)=2時,則有 φ(x)=2,φ(y)=3或φ(x)=3,φ(y)=2. 當φ(x)=2,φ(y)=3時,則有 2φ(xyz)=5+φ(z), 由引理3知,方程無解. 當φ(x)=3,φ(y)=2時,則有 2φ(xyz)=5+φ(z), 由引理3知,方程無解. 綜上所述,證畢.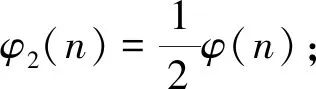
2 結論及證明