一類隨機遞歸神經網絡的穩定性分析

郭旭暉,姚志易,馬維軍

(寧夏大學 信息工程學院， 寧夏 銀川 750021)

近年來，遞歸神經網絡在組合優化、模式識別等領域得到了廣泛的應用[1-3]，引起了人們的廣泛關注.由于神經網絡的動力學行為常常受到隨機和時滯等因素的影響，導致系統失穩或震蕩.然而在工程應用中要求網絡必須是穩定的，因此對于具有時變時滯的隨機遞歸神經網絡的穩定性研究，無論是在理論研究還是實際應用中都十分重要.很多學者對隨機遞歸神經網絡進行了大量研究[4-5]，然而關于其優化問題的研究結果相對較少.到目前為止，還沒有關于具有時變時滯的隨機遞歸神經網絡逆最優控制的相關研究成果.本文基于逆最優方法和Lyapunov函數，針對一類具有時變時滯的隨機遞歸神經網絡模型，討論了其全局漸近穩定性問題.

1 模型描述

考慮如下具有時變時滯的隨機遞歸神經網絡模型

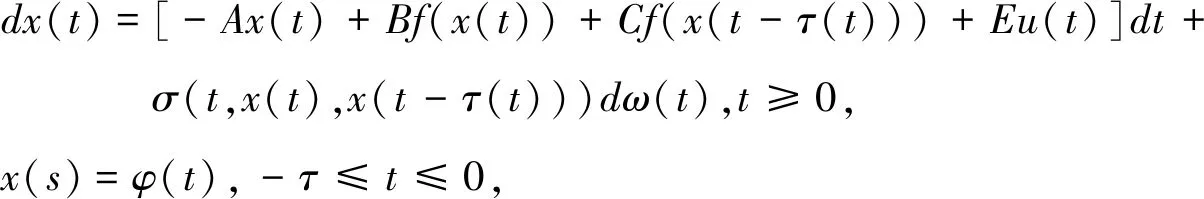
(1)

其中,x(t)=(x1(t),x2(t),…,xn(t))T∈Rn表示狀態向量，A=diag(δ1,δ2,…,δn)是一對角矩陣且δi>0,i=1,2,…,n,B=(bij)n×n和C=(cij)n×n分別表示反饋矩陣和時滯反饋矩陣，τ(t)表示時變時滯，f(x(t))=(f1(x1(t)),f2(x2(t)),…,fn(xn(t)))T∈Rn表示非線性激勵函數，E是具有適當維數的控制輸入矩陣，u(t)為控制輸入，σ(t,x(t),x(t-τ(t)))∈Rn×n表示噪聲強度函數，ω(t)∈Rn是一個n維獨立標準的Wiener過程.

假設激勵函數fj(xj(t))，時變時滯τ(t)和噪聲強度函數σ(t,x(t),x(t-τ(t)))滿足以下條件.

(A1)?x,y∈R,?kj>0,使得|fj(yj)-fj(xj)|≤kj|yj-xj|;j=1,2,…,n.

(A2)σ(t,x(t),x(t-τ(t)))是全局Lipschitz連續且滿足Tr{σ(t,x(t),x(t-τ(t)))Tσ(t,x(t),x(t-τ(t)))}≤‖M1x(t)‖2+‖M2x(t-τ(t))‖2,其中，Tr表示矩陣的跡，M1∈Rn×n和M2∈Rn×n為矩陣.

(A3)fj(0)=0;σij(t,0,0)=0;i,j=1,2,…,n.

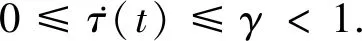
定義[6]對于一般的隨機非線性系統

dx=F(x)dt+G1(x)udt+G2(x)dω,

(2)

其中,x∈Rn表示n維狀態，u∈Rp表示狀態輸入，ω∈Rq是一個獨立標準的Wiener過程.

如果存在滿足以下Hamilton-Jacobi-Bellman(HJB)方程的正最優值函數V(x)

(3)

則

(4)

是可以最小化性能函數的最優穩定控制

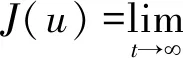
(5)

其中,對于所有的x，q(x)≥0和R(x)≥0.

2 主要結果

在開始證明定理之前，先對Lyapunov函數進行簡單計算.

對系統(1)構造如下Lyapunov函數

(6)

由假設(A1-A4)及不等式2xy≤xTx+yTy，利用It可得

≤-δxT(t)x(t)+xT(t)Eu(t)+

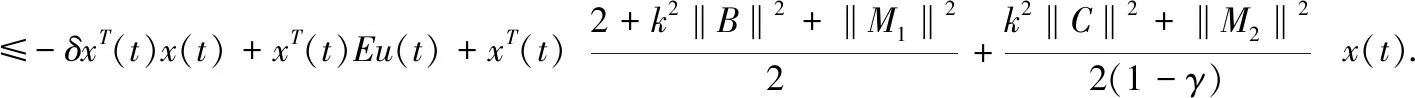
(7)

選擇控制輸入如下

(8)

將(8)代入(7)可得

LV≤-δxT(t)x(t)≤0.

因此，控制輸入(8)是一個穩定控制.

根據非線性最優控制，將Lyapunov函數(6)作為最優值函數代入HJB方程(3)可得

(9)

在穩定控制輸入(8)的基礎上，定義了一個新的控制(即對控制輸入(8)進行簡單修正)，

(10)

其中,λ>2是一個常數.

由(3)和(7)可得

(11)

則

xT(t)[-Ax(t)+Bf(x(t))+Cf(x(t-τ(t)))+Eu(t)]-

(12)

定理對于系統(1)，存在正定函數q(x)(12)和嚴格正函數R(x)(11)，使系統(1)通過反饋控制律

(13)

在原點達到全局逆最優，并使性能函數最小化

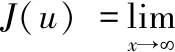
(14)

因此，最優控制律(即控制輸入)能使系統(1)達到全局漸近穩定.

證明根據Lyapunov函數(6)，系統(1)的無窮小生成元為

(15)

將控制輸入(13)代入(15)可得

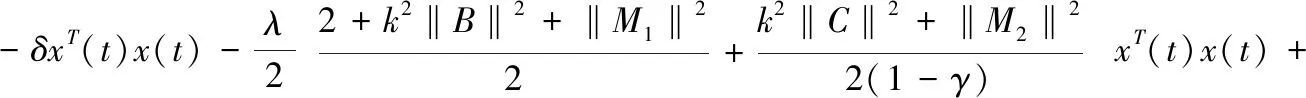
≤0,?x≠0.

(16)

系統(1)通過控制器(13)在x=0處達到全局漸近穩定狀態.

下面，對q(x)和R(x)進行討論.

由(12)可得

(M2x(t-τ(t)))-xT(t)[-Ax(t)+Bf(x(t))+Cf(x(t-τ(t)))+Eu(t)]-

(17)

在上述中可知，δ>0,λ>2.則q(x)是正定的和徑向無界的.

由(11)可得

(18)

如果|E|≠0，則ETE>0，R(x)>0.通過選擇q(x)(12)和R(x)(11)，LV可表示為

LV=-q(x)-uTR(x)u+(u-u*)TR(x)(u-u*).

(19)

由文獻[7]可得

(20)

根據(16)可得，最優控制u=u*是有意義的成本函數J的最優解.

備注1 本文通過構造適當的Lyapunov函數，給出了穩定控制(10).由于控制器的設計與參數有很大關系，在實際應用中，當激勵函數的權值和Lipschitz系數均為常數時，通過選擇合適的參數λ，使(11)中的R(x)變為常數，則控制輸入(11)就變成了易實現的常數狀態反饋控制器.

備注2 在控制工程應用中，最優系統具有許多良好的特性，如穩定性、魯棒性、降低靈敏度等[8].然而一般隨機非線性系統(2)的HJB方程(3)的解很難求得，在很多情況下，HJB方程沒有解或不存在唯一解.因此，逆最優方法為求解非線性系統的最優控制問題提供了可能，這種方法的優點是不需要求解HJB方程.

備注3 文獻[9]和文獻[10]中指出，逆最優控制方法是仿生學神經網絡領域最有效的方法之一.然而，在特定任務中優化確切的成本函數并不總是清楚的.因此，如何設計合適的控制器使所考慮的系統達到穩定狀態，并使系統的成本函數達到最優，是研究非線性系統穩定性與控制十分重要的課題之一.

3 結論

本文對一類具有時變時滯的隨機遞歸神經網絡提出了一種新的全局漸近穩定控制方法.因為求解HJB方程十分困難，很難設計出反饋控制器來實現非線性系統的穩定性.本文基于Lyapunov函數和逆最優方法，我們得到了在逆最優控制下的具有時變時滯的隨機遞歸神經網絡的全局漸近穩定控制的充分條件.此外，本文的方法也可以推廣到文獻[5]的模型.