利用GeoGebra軟件揭示彩虹和霓的成因

申強強

阜陽市紅旗中學，安徽 阜陽 236000

雨后的天空有時會出現彩虹或霓，這美麗的天象其實是一種光的反射和折射現象。在學習了光的反射和折射定律后，學生可以對霓虹的成因做簡要分析，但是對于“為何霓會出現在彩虹的上方”“彩虹的顏色排布順序是外紅內紫，而霓的顏色排布順序則剛好相反”等問題難以準確解答。

GeoGebra是一款優秀的動態數學軟件，它擁有強大的數學運算和圖形處理能力。利用GeoGebra可以動態演示彩虹和霓形成過程的光路，更加方便、直觀地揭示彩虹和霓的形成原理。

1 彩虹的形成原理

1.1 彩虹形成原理的GeoGebra演示

在雨后或者其他合適的氣象條件下，空氣中懸浮著大量的小水滴，陽光照射到水滴上，經過兩次反射和一次折射，形成我們看到的彩虹。下面我們將結合光的反射和折射定律，利用GeoGebra軟件演示光線在水滴中的傳播過程。

（1）任取一點O作為圓心，作一個半徑為1的圓代表小水滴。在圓上任取一動點A作為入射點，在指令欄輸入：射線（A，向量(-方向向量(x軸)))，即可得到以A為入射點的一條入射光線。

（3）在指令欄輸入：射線（C，向量（旋轉（方向向量（直線（O，C）），-α））），得到出射光線，如圖1所示。

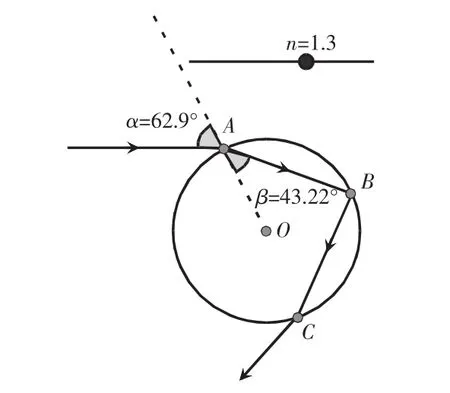
圖1 GeoGebra演示的光線在水滴中的折射和反射光路圖

至此，我們得到了某一條入射光線在水滴中經過兩次折射和一次反射的光路圖。設置線徑、顏色和線型等參數可以使效果更美觀。

眾所周知，不同單色光的折射率不同，拖動滑動條n，會發現不同折射率的單色光偏折的情況略有不同。當取n=1.33時，演示的是紅光的折射和反射光路圖A→B→C。再按照上面的步驟，將n替換為1.34，即可作出紫光的折射和反射光路圖A→D→E，如圖2所示。

圖2 一條紅色和紫色單色光的反射和折射光路圖

我們可以看到由于紅光和紫光折射率不同，二者的出射光線并不重合，且紫光在紅光的上方，這似乎與我們日常觀察到的彩虹上紅下紫的順序恰好相反。圖2只展示了一條入射光線的情況，實際上，陽光可以視為一束平行入射光線。下面以紅光為例，演示一束平行光照射到水滴表面后的傳播情況。

選中設置好的四條光線，右鍵選擇跟蹤功能，再選中A點，右鍵選擇啟動動畫，A點開始移動，左下角出現開關鍵，當A點移動到適當位置點擊暫停（圖 3）。

從圖3可以看出，當一束平行光入射到水滴表面后，經過折射和反射，在出射光線中，一部分光線折射后的角度較大，如圖中C點；還有一部分光線比較集中地出現在某一條光線的出射點附近，即圖中出射光線較密集處（如圖中D點），此處光強相對較大，被稱為彩虹線。我們看到的彩虹某一顏色的光主要來源于這密集處的光。不同顏色單色光的彩虹線所在位置不同，從而形成了彩虹外紅內紫的顏色排布。

圖3 一束平行光入射到水滴表面的折射和反射光路圖

1.2 彩虹中不同色光的彩虹角

根據光的折射和反射定律，我們可以計算出不同單色光彩虹線的位置。由圖4所示的幾何角度關系圖可以得到偏轉角

圖4 光路圖中的幾何角度關系

下面我們直接用GeoGebra畫出函數圖像，從圖像當中觀察偏轉角隨著入射角的變化有怎樣的規律，給學生更加直觀、深刻的印象。在指令欄輸入函數表達式，設置相關參數，即可得到偏轉角與入射角的函數圖像（圖5）。

圖5 彩虹中紅光偏轉角與入射角的函數關系圖

由圖5可知，在最小偏轉角附近，當入射角在較大范圍內變化時，偏轉角變化較小，此處光線較密集，光強較大，這就是我們要找的彩虹線的位置。嚴格的數學證明過程較繁雜，本文不再贅述，有興趣的讀者可自行驗證。

利用極值點工具可以找出當n=1.33時，紅光的最小偏轉角為137.48°（圖5），這就是紅光彩虹線的位置。當取n=1.34，可以得到紫光的最小偏轉角為138.93°，也就是紫光彩虹線的位置。我們也可以利用求導數找極值的方法求出（4）式所代表函數的極值點，找到對應的最小偏轉角，其結果與我們利用圖像得到的結果是一致的。

最終，我們可以得到出射光線反向延長線與入射光線方向的夾角，對于紅光是180°-137.48°=42.52°。這就是人眼對于彩虹的仰角，稱為紅光的彩虹角（圖6）。我們所看到的彩虹中紅色部分均來自于這一角度附近。同理，紫光的彩虹角為180°-138.93°=41.07°。 可見，紫光的彩虹角小于紅光的彩虹角，這就是彩虹顏色排布的順序是外紅內紫的原因。

圖6 紅光的彩虹角

2 霓形成的原理

2.1 霓形成原理的GeoGebra演示

在彩虹的上方，我們有時還能看到另一條與彩虹顏色順序相反的“副虹”，即我們常說的“霓”。彩虹是光在水滴中經過兩次折射和一次反射的結果，而霓的形成則是入射光線在水滴內多發生了一次反射，導致它的顏色排布順序與彩虹恰好相反。霓形成原理的GeoGebra演示在彩虹的基礎上增加以下步驟：

（1）在指令欄輸入：交點(c，射線(C，旋轉(旋轉(旋轉(O，β，A)，2β，B)，2β，C))，2)，得到出射點F，連接 CF。

（2）再輸入：射線(F，向量(旋轉(方向向量(直線(O，F))，-α)))，得到出射光線。

（3）設置好相關光線的顏色和樣式使界面更美觀。如圖7所示，仍以紅光為例，取n=1.33，拖動A點，即可觀察到不同角度入射光線的偏轉情況。

圖7 GeoGebra演示霓形成原理的光路圖

2.2 霓中不同單色光的彩虹角

與彩虹類似，我們也可以求出霓中不同單色光的彩虹角。由幾何關系可得偏轉角

我們仍用GeoGebra畫出函數圖像，與彩虹類似，在霓中各單色光偏轉角的極大值附近，入射角在較大范圍內變化時，偏轉角變化較小，意味著此處光線密集，光強較大，這就是霓中各單色光彩虹線的位置。

利用極值點工具可找出紅光偏轉角的最大值為129.9°，如圖8所示。當n=1.34時，可以得到紫光偏轉角的最大值為127.29°。由此可以計算出霓中紅光的彩虹角為 180°-129.9°=50.1°，紫光的彩虹角為 180°-127.29°=52.71°。 所以，在霓中不同單色光的排布順序是外紫內紅，與彩虹的顏色排布順序相反，且由于霓中各單色光的彩虹角均比彩虹中同一單色光的彩虹角大，所以它在彩虹的上方出現。

圖8 霓中紅光偏轉角與入射角的函數關系圖

以前對于彩虹和霓成因的解釋，學生往往只能畫出某一條單色光線在水滴表面折射和反射的光路圖，難以做出更深入的分析。而利用GeoGebra軟件可以動態演示彩虹和霓的形成原理，并且可利用GeoGebra繪制圖像，找出彩虹和霓中不同單色光的彩虹角，更直觀地解釋了彩虹和霓中單色光排布順序等問題。GeoGebra軟件功能強大，除了光學問題，它還能幫助我們動態、直觀地演示其他很多物理問題，如帶電粒子在磁場中的偏轉問題以及演示簡諧振動和機械波等物理問題[1]。