基于BP神經網絡的橫流式蒸發冷凝器鼓泡式板片傳熱性能預測*

上海理工大學 上海市動力工程多相流動與傳熱重點實驗室 席鵬飛 章立新 張坤龍 陳 權 周慶權 高 明 劉婧楠 陳永保

浙江三新科技有限公司 潘旭光 陳婷婷

0 引言

板式蒸發冷凝器在制冷過程中的工作原理是將板內高溫氣態制冷劑的冷凝熱傳遞到板外表面的水膜中，水膜與空氣間再通過對流的顯熱傳遞和蒸發的潛熱傳遞最終將熱量散發到大氣中。

在蒸發冷凝器中，有工質與壁面間對流與凝結換熱、壁面熱傳導、水膜與壁面對流換熱、水膜熱傳導、水膜與空氣的顯熱與潛熱交換這一系列換熱環節，在這些環節中，蒸發側(即水-空氣側)的熱阻一般最大，因此強化傳熱的重點在于水-空氣側傳熱的優化。與平直板片相比，凸凹結構的板片增強了擾流，破壞了邊界層，同時增大了換熱面積。鼓泡式板片通道類似于長方形狹窄通道，通常通道內的流動處于低雷諾數湍流狀態。目前關于鼓泡式板片幾何參數對板片通道內流動與傳熱的影響規律有一些研究。王定標等人提出蜂窩板的傳熱性能優于平板，用數值模擬的方法研究了雷諾數、傾斜角度對換熱性能的影響，并從場協同的角度分析了凹凸板換熱強化的原理[1-2]。張延豐等人基于多場協同原理進行了數值模擬，得出了鼓泡式板片傳熱元件的幾何參數對流動與傳熱的影響規律和優化措施[3]。Samad等人[4]、王光輝等人[5]分析了凹坑凸包的直徑、深度等幾何因素對板片的傳熱和阻力性能的影響。簡棄非等人分析了凸凹板在橫流蒸發冷凝器水-空氣側的傳熱傳質機理，并歸納了散熱量、進風狀態、冷卻水溫度等對系統能效比的影響[6]。

上述研究主要針對板片本身的幾何參數，本文針對橫流式蒸發冷凝器中特定幾何參數的鼓泡式板片的蒸發側傳熱規律，在不同板片間距、不同水膜流量、不同截面風速下，通過一定量實驗測出復合換熱系數。但因環境條件不可控，實驗的環境參數隨機，為總結和研究其傳熱規律，采用BP神經網絡進行處理，以得到實驗范圍內其他參數條件下復合傳熱系數的預測值。

BP神經網絡能夠在輸入輸出的數學模型未知的情況下，通過反向傳播進行參數學習，以此尋找網絡誤差最小化的參數組合[7]。在BP神經網絡的應用上，孫金穎等人分析了建筑節能改造案例，并確定了關鍵影響因素，通過使用BP神經網絡對現有的建筑節能改造評價體系建模，從而提出了新的適合我國國情的建筑節能改造模式[8]；李祥立等人以大連某建筑為測試對象，使用BP神經網絡對其地板供暖系統的熱負荷建模，在實際測量的供暖期不同時段的熱負荷數據基礎上，進行了預測研究，結果表明，神經網絡預測模型能夠準確預測一個單元未來24 h不同時段的熱負荷，預測誤差約為5%[9]。從這些學者的研究中可以發現，在工程實例中使用BP神經網絡進行預測是完全可行的，并且其預測精度滿足了使用需求。因此，用BP神經網絡預測鼓泡式板片的性能是可行的。

本文搭建了鼓泡式板片用于橫流式蒸發冷凝器時蒸發側傳熱性能測試實驗系統，對鼓泡式板片在不同工況下的傳熱性能進行測試，并建立了3層BP神經網絡(輸入層、隱含層和輸出層)對復合換熱系數進行預測。輸入層由5個參數組成，分別為進口空氣干球溫度和濕球溫度、噴淋水流量、截面風速、板片間距，輸出層為復合換熱系數。

1 實驗臺及部件

實驗系統的主要部件包括帶電加熱的鼓泡式板片、可變頻的風機、噴淋水泵及相應的風道和水管路，調節設備包括用于風機的變頻器、用于電加熱的調壓器、用于水路的流量調節閥，測量設備包括大氣壓力計、干濕球溫度計、轉輪風速儀、浮子流量計和熱電偶等。圖1為實驗臺布置實物圖，圖2為流程簡圖。圖3a為鼓泡式板片的表面實物圖，鼓泡式板片高740 mm，寬240 mm，材料為碳鋼，加工前的基板厚2 mm，凸包高2 mm、直徑10 mm，凸包布置如圖3b所示。熱源為埋于板片內的電加熱線，冷源為環境空氣。所測的鼓泡式板片試件主要由鼓泡板、導熱泥、電加熱線、保溫材料、背板組成，如圖4所示。因鼓泡式板片材質的導熱系數大且壁薄，可忽略板材的傳導熱阻，以板內側壁溫代表板的表面溫度，故在板的內側壁上均勻布置16個銅-康銅熱電偶，熱電偶線直徑為0.3 mm，其熱端與板的內側壁緊貼，用導熱泥壓緊，冷端置于冰水混合物中。在導熱泥中埋入電加熱線，導熱泥可起均勻溫度作用，導熱泥后覆蓋絕熱板，并在背板與鼓泡板的接縫間加密封墊后通過螺栓連接，壓實導熱泥、電加熱線、絕熱板，并保證試件不漏水。在背板內側(即背板與絕熱板間)也布置了一對熱電偶，以監測其是否漏熱。2個相同的鼓泡式板片試件對置，構成蒸發冷凝器的蒸發側通道，通道結構的特征為板片的凸點對凸點、凹點對凹點，且板片間距可調。每個試件的上沿各有一個蓄水槽，長度與板片寬度相等，蓄水槽內的紗布引導噴淋水自上而下流出，即每側板片上的水膜流量是噴淋水管路上浮子流量計讀數的一半，本文計算所用流量是兩側板片上的總流量。板片間距D為凹點的間距(即流道最大間距，因為板片壓制時，四周法蘭面與凹點平齊)，而截面風速則取板片間截面的平均風速(即計算風道橫截面時取兩板片凹點與凸點中位面間的距離D0，并忽略水膜厚度)。D和D0見圖4。

圖1 實驗臺布置

圖2 實驗臺流程簡圖

圖3 鼓泡式板片

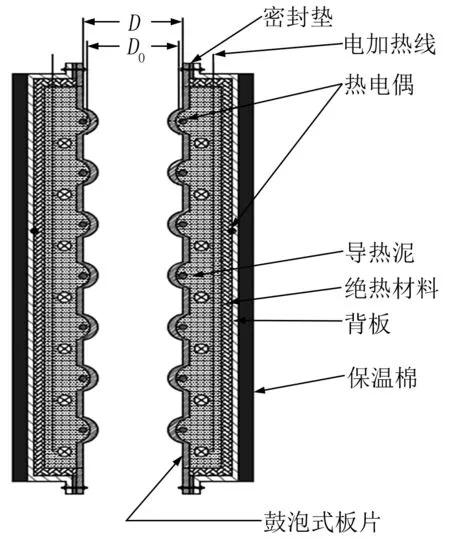
圖4 試件結構示意圖

實驗臺運行時，由噴淋水泵將噴淋水從水池輸送至試件頂部的布水器，布水器將水均勻布灑在鼓泡式板片上沿，并沿板片表面形成一層薄水膜，水膜因重力向下流動，最后沿板片的下邊沿流到水池中。空氣在風機作用下，從板片試件一側豎邊流入，與噴淋水直接接觸并呈橫向交叉流動，然后從另一側豎邊流出，經過風量測試段后從風機排出。風量測試段位于風機下方，為一矩形腔，設有3個風速測點，根據所測風速的平均值和該矩形腔截面積可算出風量，從而換算得出板片通道的截面風速。

待水、氣運行穩定后，調節電加熱功率，使板片溫度保持為60 ℃，實驗中板片上熱電偶的溫度基本一致，證明板片壁溫分布均勻，本文所做的試件采用電加熱模擬冷凝放熱是成功的。大氣壓力由空盒氣壓計測得，進出口空氣干濕球溫度分別由鉑電阻溫度計、濕球溫度計測得。

2個板片壁面上分別均勻設置了16個熱電偶溫度測點，以熱電偶所測溫度的平均值作為板片溫度；板片外殼與保溫棉間設置了2個熱電偶，測量外殼溫度，以計算外殼散熱熱損失；因難以準確測量板片表面噴淋水膜的溫度分布，在板片上的蓄水槽和板片下端的出水部位各設置了1個熱電偶來測溫，分別視為噴淋水的進口和出口溫度；進、出口空氣的干、濕球溫度由干濕球溫度計測得。以上數據的采集方式均為每分鐘采集60組數據并取其平均值記錄。

實驗中采集樣本數據的范圍見表1。

表1 實驗數據范圍

空氣帶走的熱量為

(1)

式中Qa為空氣帶走的熱量，kW；Goa為出口空氣的體積流量，m3/h；ρoa為出口空氣的密度，kg/m3；hoa、hia分別為出口、進口空氣的比焓，kJ/kg。

平均溫差取板片溫度與板片上噴淋水膜表面空氣濕球溫度的對數平均溫差，也稱為濕溫差。設板片的平均溫度為tw，空氣進、出口的濕球溫度分別為twbi、twbo，則定義

Δtmax=tw-twbi

(2)

Δtmin=tw-twbo

(3)

平均溫差Δt可由下式計算得出：

(4)

系統內的主要傳熱環節有2個：

1) 電加熱產生的熱量通過換熱板片傳遞給板片外側的水膜。

2) 板片表面覆蓋的水膜與空氣的熱質交換將熱量傳遞到空氣中。

待系統穩定運行后，進口水溫等同于出口水溫，因此可認為進出口空氣的比焓差數值等于板片的散熱量數值,用式(5)計算板片與空氣間的復合換熱系數K[10]：

(5)

式中A為板片單個表面的換熱面積。

熱平衡偏差β的計算式為

(6)

實驗方案見表2。

表2 實驗方案

實驗系統循環穩定后，每分鐘記錄1次數據，每個工況共記錄5組，調節噴淋水流量、風機頻率、板片間距來改變工況，最終共獲得175組測試數據。

2 網絡建模

2.1 網絡原理與參數設置

從結構來看，BP神經網絡一般由3層組成，即輸入層、隱含層和輸出層。BP算法的學習過程有正向傳播和反向傳播2個過程：在正向傳播過程中，從輸入層開始到隱含層、輸出層依次計算各層各節點的實際輸入、輸出，這個過程中，每一層的神經元只會被上一層的神經元所影響，所以也稱為多層前饋階段；若輸出層不能取得期望值，則進入反向傳播過程，即根據輸出層神經元的輸出誤差，沿路反向修正各神經元之間的權重和閾值，從而使得輸出值逼近期望值，所以也稱為反向誤差修正階段。

按照隱含層的數量，BP神經網絡可分為單隱含層網絡和多隱含層網絡。一般來說，單隱含層BP網絡已經能夠滿足映射任何有理函數的需求，此外，雖然增加隱含層的層數可以使誤差更小，提高精確度，但同時也會使網絡復雜化，導致訓練網絡權值的時長大大延長；同時，增加隱含層神經元數量也可以提升預測精度，并且其訓練結果比增加層數的方法更容易發現和調整[11-12]。因此，本文采用單個隱含層的BP神經網絡，其結構如圖5所示，而隱含層神經元的數量則由下文的計算擇優選取。

圖5 單個隱含層的BP神經網絡結構示意圖

K值的大小不僅與平均溫差有關，還與噴淋水流量、截面風速、板片間距及進口空氣的干球溫度和換熱區間的氣壓等相關。根據以往經驗，在開放式系統中，氣壓影響較小，本文將該因素的影響忽略不計；作為蒸發式冷凝器，本文以60 ℃的冷凝溫度為應用背景。輸入層中選取了5個影響因素作為輸入參數，分別以進塔空氣干球溫度ti、進口空氣濕球溫度twbi、噴淋水流量Q、板片間截面風速vair、板片間距D為輸入值，復合換熱系數K為輸出值。圖5中Wmnk代表第m層的第n個神經元到第(m+1)層的第k個神經元的連接權重，在迭代時會按式(7)沿梯度下降方向進行更正[13]：

(7)

式中η為學習效率，取值為0.1；E為目標網絡中所有誤差的平方和。

2.2 性能評價指標

使用相關系數R、平均相對誤差MRE和均方根誤差RMSE來評價預測模型的性能。相關系數R的范圍為[0,1]，越接近1，參數間相關性越大。平均相對誤差MRE、均方根誤差RMSE的計算式分別為

(8)

(9)

式(8)、(9)中N為樣本容量；ai為實際的輸出值；pi為預測的輸出值。

洋山港主航道附近島嶼眾多，急漲水時，由于受汊道的影響，筲其島和顆珠山附近的流向與主航道走向夾角可達20°，會導致重載船的操縱能力變差。港內航道邊界緊鄰碼頭泊位，錨地稀少，可僅供1艘大型船舶應急使用。目前，每天約有30艘大型船舶進行靠離泊作業，若大型船舶在發生緊急情況，幾乎沒有可用于大幅轉向避讓的可航水域。

2.3 網絡訓練與優化

網絡訓練學習的流程如下：1) 訓練的初始，將隨機值賦予各神經元之間的權值系數；2) 比較輸出值與期望值的偏差，并改變各神經元間的權值；3) 誤差或迭代次數達到預設值，則網絡訓練完成。

本文的訓練算法采用traingd算法，該算法的特點是批梯度下降訓練函數，從參數的負梯度方向調整權值、閾值；隱含層的傳遞函數為sigmoid函數，其定義式為

(10)

輸出層采用線性傳遞函數。隱含層節點數的選擇關系到網絡訓練的準確度和效率，節點數過多則神經網絡過于復雜，計算量增大，延長收斂時間；節點數過少則無法保證訓練的精確度。本文借鑒“黃金分割法”的概念[14]，隱含層的節點數范圍由下面的經驗公式來確定：

(11)

式中a、b分別為隱含層節點數的最小值、最大值；ni、no、ny分別為輸入層、輸出層、隱含層的節點數。

以下為采用黃金分割法搜索最佳隱含層節點數的步驟:

1) 本文中，ni=5，no=1，因此代入式(11)得出a=3，b=16。在區間[3,16]上確定第1個點的位置x1=a+0.618(b-a)=11.034，取x1=11并記錄該點對應的誤差。

2) 第2個點位置，x2=a+0.382(b-a)=7.966，取x2=8，記錄該點對應的誤差。

3) 比較x1、x2點對應的誤差的大小，因x1點的誤差較小，則留下區間[x2,16]。

4) 在區間[x2,16]上重復以上過程，比較點3、16、11、x1、x2等對應的誤差，最終得到ny=16為區間[3,16]上最優值。

5) 用黃金分割法求得拓展區間[16,24]，右端值c根據16=3+0.618(c-3)取得。重復步驟1)～4)，最終求得區間[16,24]上的最佳值為ny=18。

6) 比較ny=16和ny=18時的誤差，最終選取誤差值較小的ny=16。

不同節點數的R、MRE和RMSE值見表3。

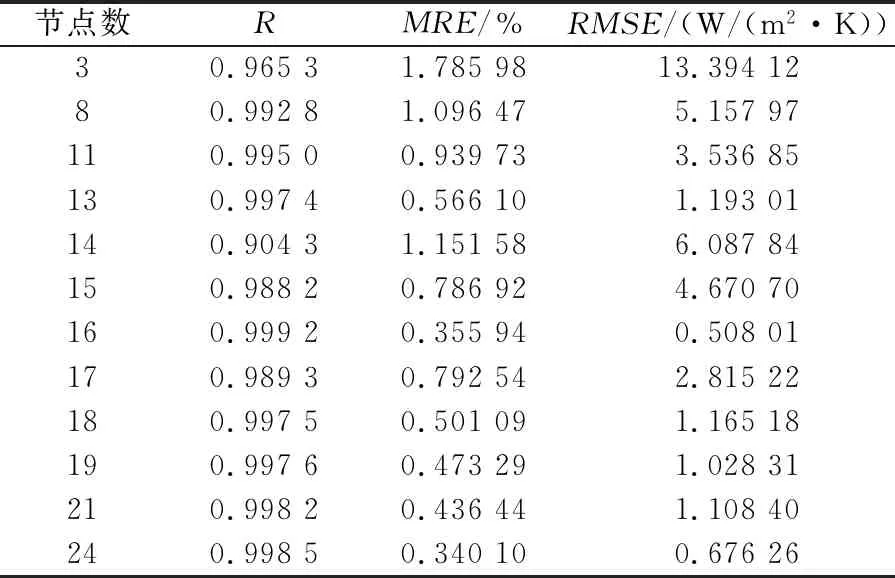
表3 不同節點數的評價指標

從表3可以看出，當隱含層節點數為16時，實測值與預測值的相關系數R較大且MRE與RMSE較小，因此本文中的隱含層節點數確定為16。為了減少訓練的時長、減小誤差，對樣本的數據進行歸一化處理；同時，數據在輸出后需要反歸一化處理。選取mapminmax函數作為歸一化函數，歸一化、反歸一化表達式分別為

(12)

x=xmin+y(xmax-xmin)

(13)

式(12)、(13)中x為被歸一化的值；xmin、xmax分別為x中的最小值、最大值；y為歸一化后的值。

3 計算結果分析

建立BP神經網絡模型，使用記錄的175組試驗數據中隨機的150組進行模型訓練，剩余的25組用于驗證模型的精確程度。

圖6顯示了不同工況點(工況點指不同進口空氣干球溫度和濕球溫度、噴淋水流量、截面風速、板片間距工況下測得的數據組，下文的“樣本點”則是指所有工況點中被用作訓練神經網絡的一部分)下板片與空氣間復合換熱系數的預測值與實測值的對比。由圖6可以看出，絕大多數預測值與實測值的偏差較小。評價標準有相關系數R、平均相對誤差MRE、均方根誤差RMSE，分別為0.999 2、0.355 94%、0.508 01 W/(m2·K)，最大的偏差為1.521 27 W/(m2·K)，最大偏差百分比為1.038 95%。

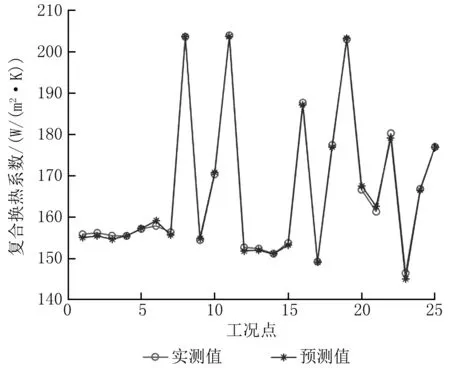
圖6 復合換熱系數K的預測值與實測值的對比

少數工況點處復合換熱系數誤差較大的原因可能是該點附近的訓練數據較少，神經網絡對這些樣本點的訓練并不充分；而那些預測準確性較高的點，其附近的訓練數據足夠多，神經網絡對此處的訓練足夠充分。因此，若在后續的研究中對實驗參數變化范圍內的工況進行細化實驗，獲取更多的數據，將能進一步提高工況點預測的準確度。在橫流式蒸發冷凝器中鼓泡式板片傳熱性能研究領域，BP神經網絡可用于驗證實驗、數值模擬結果的準確性，并為進一步的鼓泡式板片設計優化和橫流式蒸發冷凝器的改進提供參考。

圖7顯示了平均相對誤差MRE隨迭代次數增加的變化趨勢。由圖7可以看出，訓練過程中隨著迭代次數的增加，平均相對誤差總體下降，并趨于穩定。

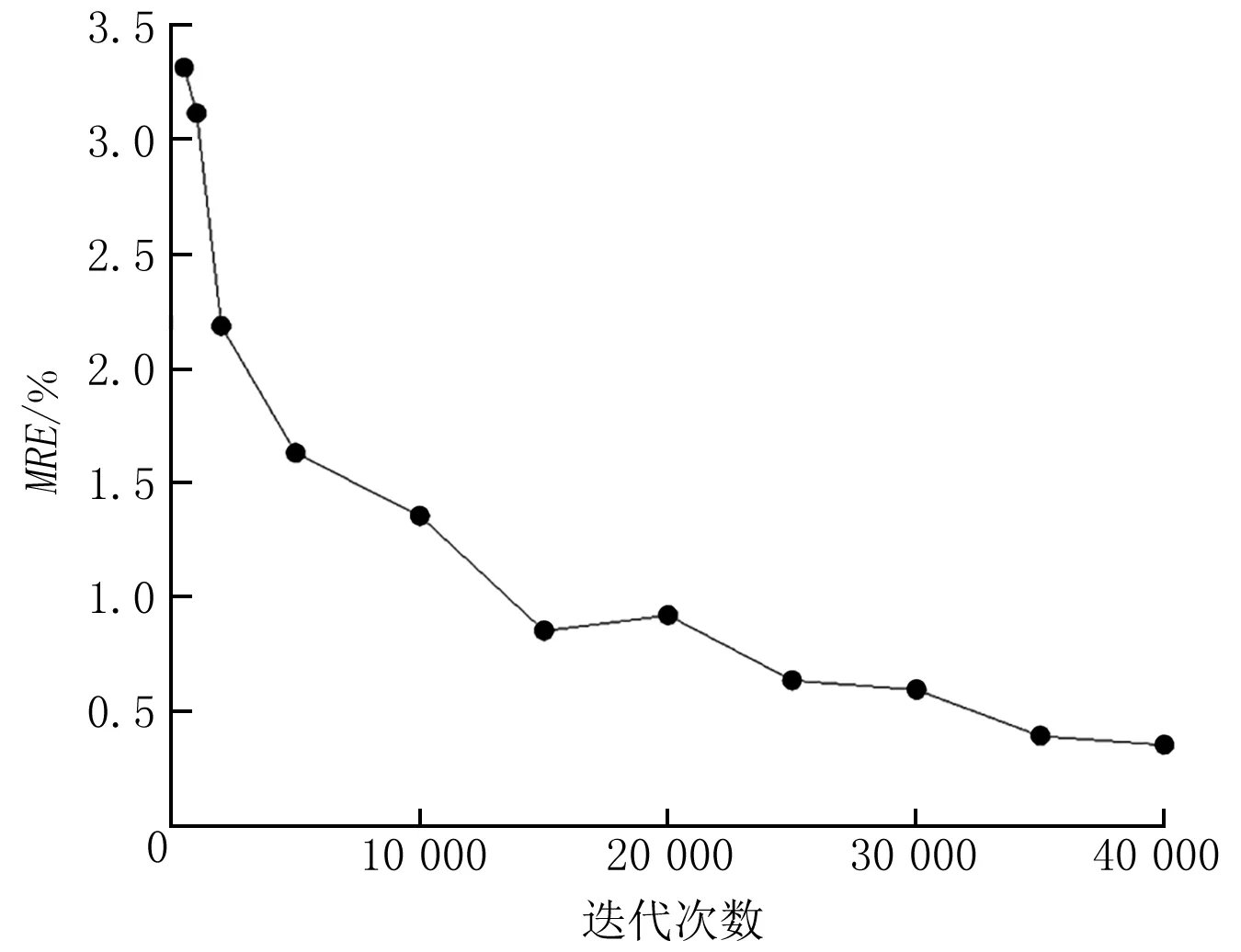
圖7 平均相對誤差隨迭代次數的變化(學習速率0.1，訓練函數traingd，隱含層神經元數16)

4 結語

根據鼓泡式板片在蒸發冷凝器蒸發側的運行工況搭建了實驗臺，并基于BP神經網絡建立了其在水-空氣側傳熱性能的預測模型。采用3層BP神經網絡，以進口空氣干球溫度、進口空氣濕球溫度、噴淋水流量、截面風速及板片間距為輸入層，以Sigmoid函數與線性傳遞函數分別作為隱含層和輸出層的傳遞函數；隱含層神經元數為16，訓練函數為traingd，輸出參數為板片與空氣間的復合換熱系數，選取的迭代次數為40 000次。

影響鼓泡式板片換熱性能的參數較多，使用BP神經網絡在給定的輸入輸出參數基礎上調整各神經節點的權值，從而對不同工況下的鼓泡板片復合換熱系數進行預測，而不需要進行煩瑣的全部實驗流程。

以相關系數、平均相對誤差、均方根誤差作為網絡評價指標，結果分別為0.999 2、0.355 94%、0.508 01 W/(m2·K)。在鼓泡式板片換熱性能測試方面，本文建立的BP神經網絡模型的預測結果與實驗測得的換熱系數相差很小，為不同工況下鼓泡式板片換熱性能的預測提供了參考。