零能耗光伏并網建筑的獎懲機制建立和應用研究*

安徽工業大學 孫瑞瑞 魯月紅 季海霞 黃志甲

0 引言

隨著發展中國家經濟水平的不斷提高，建筑行業能耗將快速增長，預計到2040年，將占能源消費總量的1/3，新增的能耗幾乎全部是電耗[1]。聯合國第五次氣候變化評估報告顯示，建筑行業碳排放量占全球碳排放量的70%[2]，因此，建筑行業應對全球高碳排放量負主要責任。不斷增長的電力消費是將能源與環境領域問題相聯系的一個重要促成因素。在這一背景下，綠色建筑和零能耗建筑的推廣對建筑節能減排及可持續發展具有促進作用。

近年來，中國、德國、英國、丹麥等國家在可再生能源技術的發展與應用方面進行了大量的研究[3-6]。財務激勵政策，如投資補貼、凈計量方案和上網電價補貼，被認為是可再生能源獲得廣泛應用的主要促進因素。2013年，我國出臺了統一的光伏上網電價補貼政策，隨后又推出了區域上網電價補貼政策(feed-in tariff, FIT)[7-8]。Winter等人對2010—2017年德國家庭電費支出進行了分析，發現裝有光伏系統的用戶通過FIT政策獲得的收益不僅能補償逐年增長的可再生能源附加費，而且能獲得一定的凈收入[9]。2010年以來，英國實行的FIT政策有效促進了小型光伏系統(≤10 kW)在住宅中的應用，至2016年累計裝機量已達2 GW，且光伏安裝成本的下降將驅動這一數字快速增長[10]。Ritzenhofen等人通過量化FIT等級之間的關系，評估了實施不同FIT方案對可再生能源投資傾向的影響[11]。

在實現建筑零能耗目標過程中，利用集成于建筑中的可再生能源系統現場發電是目前應用最多的方案[12-13]。零能耗建筑的一個基本要求是建筑的現場發電量至少要滿足自身用電需求[14-15]。目前主要通過被動式設計(圍護結構、建筑朝向等)、主動式系統優化(HVAC系統能效、照明功率等)和可再生能源利用(光伏發電板、風力發電機等)實現建筑的零能耗[16]。對建筑用戶來說，零能耗建筑初投資是制約其是否安裝可再生能源系統的主要因素。由于可再生能源發電政策逐步進入補貼退坡階段，用戶對可再生能源系統的投資收益也越來越少，使得建筑年發電量難以與年能耗之間達到平衡[17]。為解決這一問題，Lu等人在建筑總成本中引入獎懲成本，加入獎懲成本后安裝了可再生能源系統并達到零能耗目標的建筑最終總成本僅為無可再生能源系統時的1/3[18]。獎懲機制(reward-penalty mechanism，RPM)不僅可以降低可再生能源發電拍賣風險[19]，而且可以緩解可再生能源系統過度發電的問題[9]。若建筑用戶能在給定的時間內達到目標要求，將會得到一定的獎金，否則將被罰款。因此，合理的獎懲機制能保證最低投資成本下的可再生能源系統可靠運行。

本文以上海地區某居住建筑為研究對象，建立獎懲函數并將其應用于零能耗建筑的設計中，通過給予達到零能耗目標的建筑用戶一定的獎金或對非零能耗建筑用戶收取一定的罰金，從而實現建筑的環境友好性，并在經濟上達到最優。

1 研究方法

1.1 確定問題

FIT政策是促進可再生能源技術發展的有效措施。然而，在上網電價補貼逐年減少的情況下，潛在的可再生能源系統用戶對于需要安裝多少光伏板(PV)或風力發電機(WT)以獲得最大的經濟效益存在疑惑。因此，可以建立一個與零能耗等級有關的獎懲機制，為建筑用戶提供優化的可再生能源系統方案并分析建筑用戶在該獎懲機制下的經濟效益。

零能耗等級定義為建筑現場光伏全年發電量與標準建筑年能耗之比：

(1)

式中Rz為零能耗等級；EP為建筑現場光伏全年發電量，kW·h/a；Eb,s為標準建筑年能耗，kW·h/a。

Rz越大，表示零能耗等級越高，例如，Rz=1.0表示建筑全年光伏發電量等于建筑年能耗，用1.0ZEB(zero energy building level)表示。標準建筑指某一類型建筑中具有典型代表的建筑，標準建筑能耗Eb,s為建筑各用電設備逐時能耗之和。

1.2 技術路線

本文以上海地區某居住建筑為例，建立適用于并網光伏居住建筑的獎懲機制，具體路線如圖1所示。

1) 確定標準建筑能耗。可通過2種方法獲得標準建筑能耗，第1種是通過建筑能耗數據庫獲得建筑的能耗數據；第2種是基于當地典型氣象參數和相關建筑參數，將模擬的建筑能耗作為標準建筑能耗。

2) 確定獎懲函數中的未知參數。首先，根據建筑能耗與光伏發電量之間的關系，對建筑進行零能耗等級劃分，并計算對應的光伏板數量。其次，根據當前光伏板與電力的市場價格，確定光伏系統年均初投資與標準建筑的運行費用，兩者之和為建筑的常規總成本。再次，將常規總成本與零能耗等級進行曲線擬合，得到常規總成本的擬合函數。最后，假設獎懲函數為與零能耗等級有關的一元二次函數，根據方案制定者給予的3個初始條件，對獎懲函數中的未知數進行求解。

3) 驗證獎懲函數。利用蒙特卡羅方法模擬不同建筑能耗數據，或從現有的建筑能耗數據庫中選取不同的建筑，用以驗證獎懲函數的適用性。

1.3 獎懲函數

在本文中，獎懲機制是基于標準建筑建立的。考慮溫度的影響，i時刻光伏板輸出功率與入射到光伏板上的太陽輻照度成正比，有下式：

[1+kp(tC,i-tSTC)]

(2)

式中SP為光伏裝機容量,kW；Wp,i為1 kW裝機容量光伏板i時刻的實際輸出功率，kW/kW；YP為1 kW裝機容量光伏板的峰值功率，kW；fp為降額因子，取0.9；IT,i、IS分別為i時刻和標準工況下光伏板處的太陽輻照度，kW/m2；kp為溫度系數，%/℃；tC,i、tSTC分別為i時刻和標準工況(25 ℃)下光伏板溫度，℃。

建筑在i時刻與電網交換的電量為建筑逐時能耗與光伏發電量之差。建筑的運行費用為建筑運行期間電網向建筑提供電量的費用，初始成本為光伏板的年均初投資，常規總成本為運行費用與初投資之和：

Cio=Ci+Co

(3)

式中Cio為建筑常規總成本，元/a；Ci為光伏年均初投資，元/a；Co為建筑運行費用，元/a。

對常規總成本與零能耗等級之間的關系進行擬合，得到：

(4)

式中a1、b1、c1為得到的擬合常規總成本函數中的已知系數和常數。

假設在建筑年成本中引入由獎金或罰金組成的獎懲成本，則建筑總成本包括常規總成本與獎懲成本兩部分：

(5)

(b1+b2)Rz+(c1+c2)

(6)

式(5)、(6)中Crp為獎懲成本，元/a；a2、b2、c2為獎懲成本函數中的未知系數和常數；Ct為建筑總成本，元/a。

根據加入獎懲成本后的建筑總成本與常規總成本之間的關系，提供3個初始條件用于求解總成本函數式(6)中的未知參數。初始條件為

Rz=0,Ct=k1Cio

(7)

Rz=1.0,Ct=k2Cio

(8)

Ct,min=Ct|Rz=r

(9)

式(7)～(9)中k1為建筑無可再生能源系統(0ZEB)時的總成本與該建筑常規總成本的比值；k2為零能耗建筑(1.0ZEB)的總成本與該建筑的常規總成本之比；Ct,min為建筑最小總成本，元/a；r為建筑最小總成本對應的零能耗等級。

通過觀察獎懲函數在總成本調節中的作用對其效果進行評估，引入總成本變化率σ：

(10)

σ值為負/正表示此時建筑用戶會收到獎金/罰金，絕對值越大，獎金/罰金越高，對成本的調節作用越明顯。

用誤差指標δ對獎懲函數在不同能耗建筑中的應用效果進行評估，其計算式為

(11)

式中C′t為建筑在r零能耗等級下的總成本，元/a。

δ絕對值越小表示獎懲函數越適用該能耗的建筑。

1.4 蒙特卡羅模擬

為驗證所建立的獎懲機制對不同能耗建筑的適用性，提出建筑能耗等級Rb的概念，并將其定義為建筑k的年能耗Eb_k與標準建筑能耗Eb,s之比：

(12)

本文選取9個不同的建筑能耗等級(building energy consumption level，BEC)，采用蒙特卡羅方法模擬各建筑能耗等級下的逐時能耗，用以驗證獎懲函數在不同建筑能耗中的有效性。

在本研究中，假設建筑k在i時刻的能耗Eb_k,i服從正態分布，其中標準偏差為平均值的20%，如式(13)所示：

Eb_k,i～N{(Eb,s)i,[0.2(Eb,s)i]2}

(13)

2 應用分析

本文選擇一棟位于上海市的2層住宅(見圖2)為標準建筑，建立獎懲函數并研究其有效性。該建筑坐北朝南，占地100 m2，屋頂為30°傾斜的磚瓦結構。上海市處于夏熱冬暖地區，年太陽總輻射量差異較小。建筑內的電器有照明設備、電視機、計算機、洗衣機等。各電器的使用情況設定如表1所示，其中空調器在室外溫度高于30 ℃或低于10 ℃時開啟。本文選擇的光伏板初投資、運行成本分別為2 250元/kW和0，電池組件的標稱工作溫度為47 ℃，標準工況下的轉化效率為18%。假設光伏組件壽命為25 a，降額因子為0.9。光伏板設計角度固定為30°，單塊板的面積為1.64 m2。

表1 電器使用情況

室外溫度和太陽輻射是影響建筑能耗和光伏發電的重要因素，上海市月平均太陽輻射和環境溫度如圖3所示，日平均輻照量為3.62 kW·h/m2，日平均環境溫度為16.9 ℃，室外最高溫度為37.3 ℃，最低溫度為-4.7 ℃。基于表1中電器使用情況模擬的全年建筑能耗為6 983.9 kW·h，每月能耗如圖4所示。

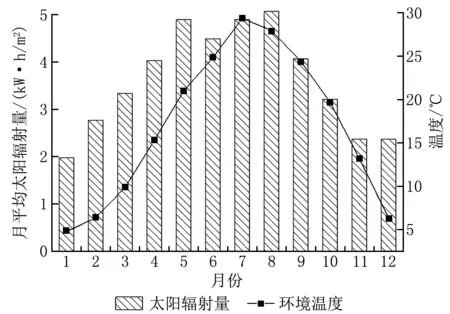
圖3 月平均太陽輻射量和環境溫度

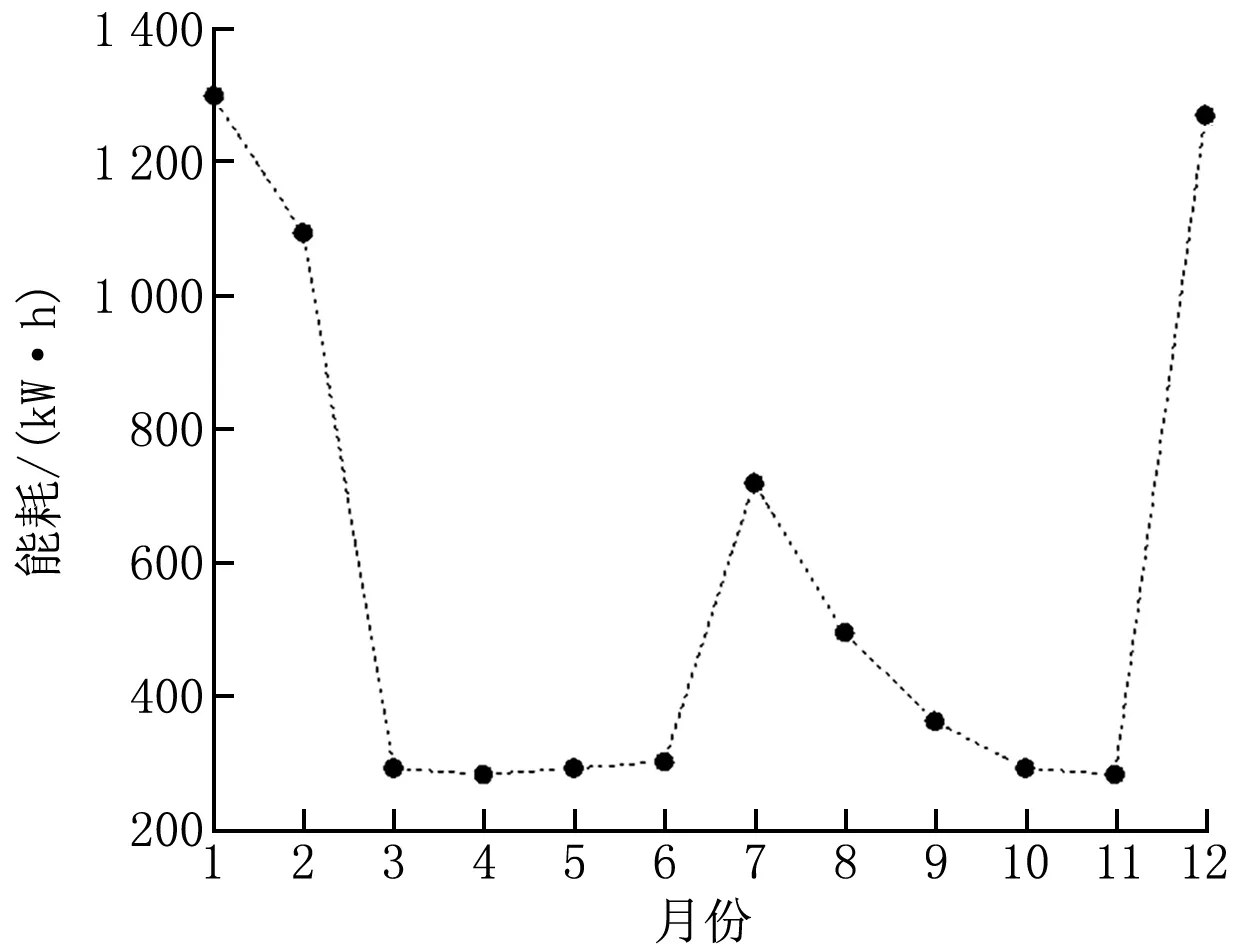
圖4 建筑月能耗

3 結果和分析

本文設計了S0、S1、S23種獎懲方案，通過對比選擇最優方案。各方案對應的初始條件中k1、k2、r值見表2。基于以上假設可求解式(5)中的未知參數a2、b2、c2。

表2 3種方案設定值

3.1 確定獎懲函數

根據表2中的假設，求解各方案獎懲函數中的未知參數，并確定獎懲函數的具體形式，如表3所示。為了驗證本文中基于標準建筑能耗設計的獎懲函數的適用性，將其應用于不同零能耗等級(0ZEB、0.2ZEB、0.4ZEB、0.6ZEB、0.8ZEB、1.0ZEB、1.2ZEB)和建筑能耗等級(0.4BEC、0.6BEC、0.8BEC、1.0BEC、1.2BEC、1.4BEC、1.6BEC、1.8BEC、2.0BEC)組合下的建筑，研究其對建筑總成本的影響。

表3 各方案獎懲函數具體形式

3.2 不同參數對建筑總成本的影響

1) 零能耗等級對建筑總成本的影響。

建筑總成本與其零能耗等級密切相關，圖5顯示了標準建筑Rb,s=1.0時總成本與零能耗等級之間的關系。從圖中可以看出，在沒有獎懲機制的情況下，建筑常規總成本隨零能耗等級的增大而增加；當引入獎懲機制時，3種方案下的總成本曲線均為凹形曲線，且分別在1.0ZEB、1.0ZEB、0.8ZEB處取得最低總成本，分別為512.5、0、476.8元/a。同時，可以預測總成本在達到最低點之后，將會隨著零能耗等級的增大而增加。

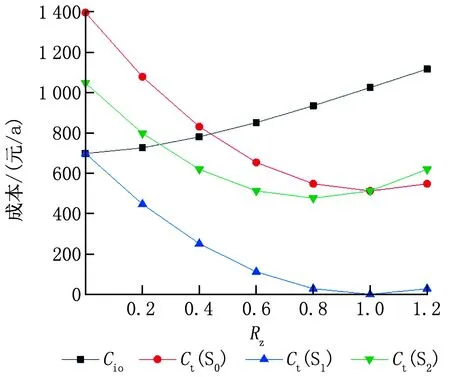
圖5 標準建筑(Rb,s=1.0)總成本與零能耗建筑等級之間的關系

此外，與常規總成本相比，不同零能耗等級下的總成本變化率是不同的，如表4所示。S0、S1和S23種方案下的成本變化率σ區間分別為-50.9%～100%、-97.5%～100%、-50.0%～50.0%。同時，方案S0、S1、S2可分別在0.6ZEB、0.2ZEB、0.4ZEB 的設計中獲得獎金，且建筑的零能耗等級越高，建筑用戶的經濟效益越高。

表4 各方案下不同零能耗等級建筑的總成本變化率

2) 建筑能耗等級對建筑總成本的影響。

為了進一步確定獎懲函數對非標準建筑總成本的影響，分析Rz=1.0時建筑總成本與能耗等級(0.4BEC～2.0BEC)之間的關系。如圖6所示，在引入獎懲函數后，3種方案下的總成本曲線與常規總成本曲線變化趨勢一致，均與能耗等級成正比。且方案S0和S2的總成本曲線重合，這是由于2個方案下的k2值相同。

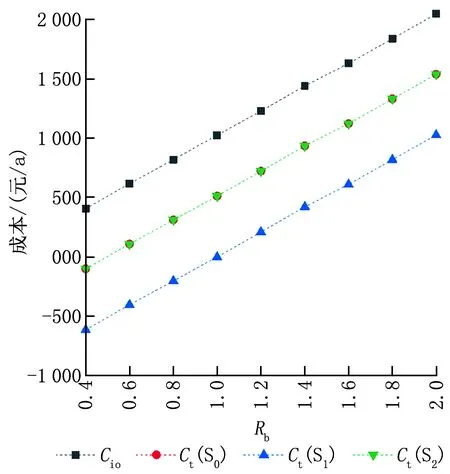
圖6 Rz=1.0時建筑總成本與建筑能耗等級之間的關系

表5顯示了不同能耗等級的建筑總成本及成本變化率比較。在3種方案中，各能耗等級的總成本均低于常規總成本，總成本變化率區間分別為-124.5%～-24.8%、-250.3%～-49.8%、-182.3%～-24.8%；且成本變化率隨著能耗等級的增大而減小，因此，當超過某一能耗等級時，獎懲函數就失去了作用。

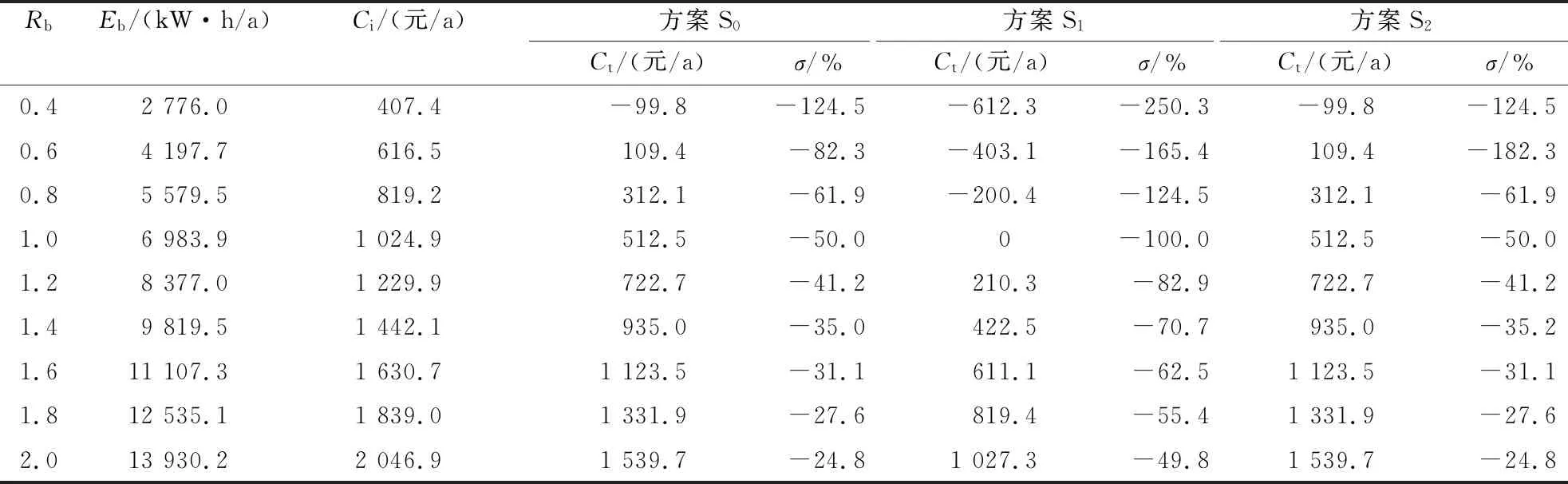
表5 各方案下不同能耗等級建筑的總成本及成本變化率

3) 零能耗等級和建筑能耗等級對建筑總成本的影響。

同時考慮零能耗等級與建筑能耗等級2個因素，研究3種方案下獎懲機制在2種因素都變化時對建筑總成本的影響，如圖7所示。在3種方案的獎懲機制下，不同建筑能耗等級下的建筑總成本變化趨勢基本一致。同一建筑能耗等級下，建筑總成本先隨著零能耗等級的增大而減小，到達某一值后隨著零能耗等級的增大而增大；同一零能耗等級下，不同建筑能耗等級建筑的總成本也存在差異，這是由不同的初投資與運行費用導致的。理想情況下，方案S0中不同能耗等級的建筑，最低總成本對應的零能耗等級應為1.0ZEB。經過分析發現，建筑能耗等級在0.4BEC～0.6BEC、0.8BEC～1.4BEC和1.6BEC～2.0BEC時，建筑總成本曲線的最低點分別位于1.2ZEB、1.0ZEB和0.8ZEB處，均位于1.0ZEB附近，因此，可以認為獎懲函數適用于能耗等級為0.4BEC～2.0BEC的建筑。

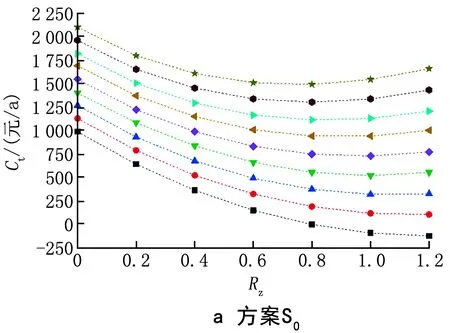
3.3 驗證獎懲函數

本文基于某一特定的標準建筑建立了3個獎懲函數，研究了各獎懲函數在不同零能耗等級和建筑能耗等級下對建筑總成本的影響。為了驗證并量化獎懲函數在不同類型建筑中的應用有效性，選擇了9個建筑能耗等級，在每個建筑能耗等級下，利用蒙特卡羅方法模擬建筑能耗100次，并取平均值作為一個建筑能耗樣本。圖8顯示了9個建筑能耗級別下48 h的平均逐時能耗。

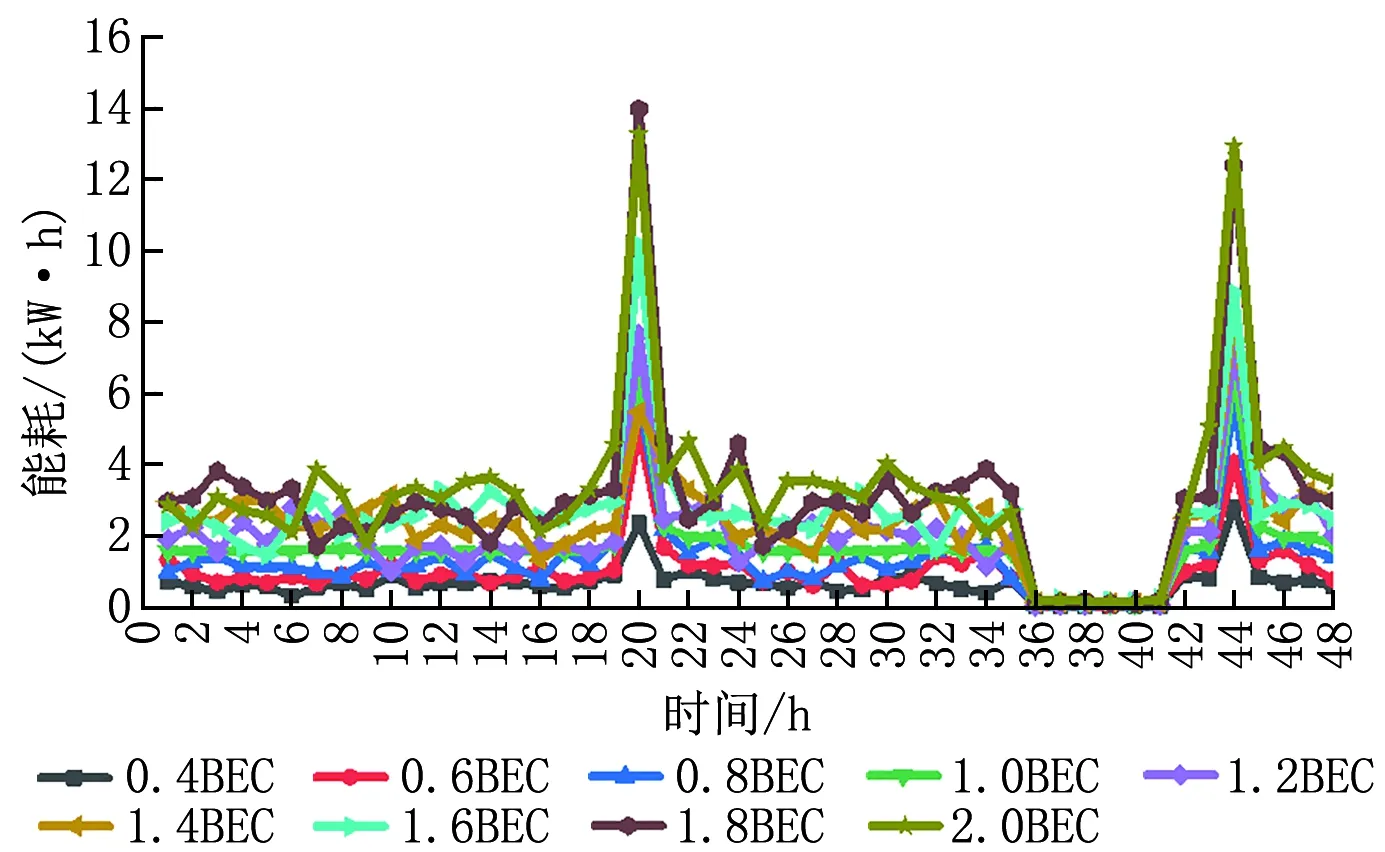
圖8 蒙特卡羅方法得到的9個建筑樣本48 h的逐時能耗

如表6所示，方案S0中，當引入獎懲機制時，建筑的最小總成本預計發生在1.0ZEB處，建筑能耗等級在0.4BEC～0.6BEC、0.8BEC～1.6BEC、1.8BEC～2.0BEC的建筑最小總成本分別發生在1.2ZEB、1.0ZEB和0.8ZEB處，除能耗等級為0.4BEC(δ=31.51%)和0.6BEC(δ=-11.42%)的建筑成本誤差較大外，其他能耗等級的建筑成本誤差均保持在4%以內。方案S1中，建筑最小總成本預計發生在1.0ZEB處，能耗等級在0.4BEC～0.8BEC、1.0BEC～1.2BEC、1.4BEC～1.8BEC、2.0BEC的建筑最小總成本分別發生在1.2ZEB、1.0ZEB、0.8ZEB和0.6ZEB處，除能耗等級在2.0BEC時偏離預計值較大外，其他均位于1.0ZEB附近，且各能耗等級的成本誤差均低于7%。方案S2中，建筑最小總成本預計發生在0.8ZEB處，能耗等級在0.4BEC～0.6BEC、0.8BEC～1.2BEC和1.4BEC～2.0BEC的建筑最小總成本分別發生在1.0ZEB、0.8ZEB和0.6ZEB處，除能耗等級為0.4BEC的建筑誤差為24.04%外，其他能耗等級的建筑成本誤差均低于4%。因此，當獎懲函數應用于能耗等級為0.8BEC～1.8BEC之間的建筑時是有效的。

表6 獎懲函數在不同能耗等級建筑中的應用有效性

3.4 獎懲機制的應用

可將本文設計的獎懲函數應用于單個居住建筑光伏系統的設計中，如圖9所示。首先，用戶可以利用能耗數據庫或能耗模擬方法獲得該建筑的年能耗，并根據自身需求選擇合適的零能耗等級，設計并選擇對應的光伏板數量。其次，計算光伏板所需的安裝面積、光伏板年初投資及建筑運行費用，并利用獎懲函數計算獎懲成本，進而獲得該建筑的總成本。最后，根據光伏板安裝所需面積和建筑總成本進行評估，若兩者均能被接受，則可通過該設計方案；否則，重新選擇光伏板數量，并重復以上步驟直到兩者均滿足要求。以標準建筑為例，零能耗等級為0ZEB、0.2ZEB、0.4ZEB、0.6ZEB、0.8ZEB、1.0ZEB、1.2ZEB時，所需的光伏板安裝面積分別為0、8.20、14.76、21.32、27.88、36.08、42.64 m2。

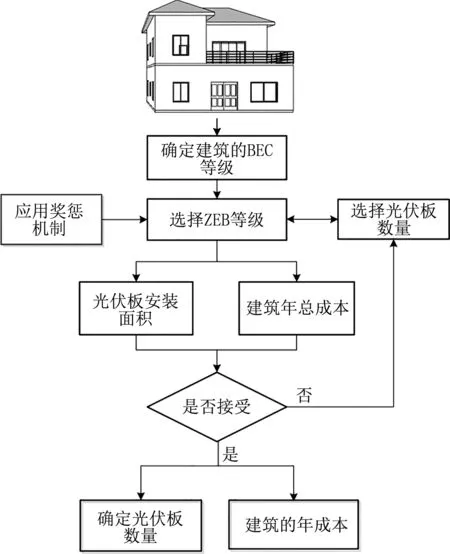
圖9 獎懲機制的應用流程圖

4 結語

本文提出了一種零能耗建筑獎懲機制設計方法，通過在常規總成本中增加獎懲成本，從而將其調整為滿足設計者需求的成本優化函數，并采用蒙特卡羅方法驗證了獎懲函數在不同建筑能耗下對總成本調節的有效性。

以上海市某居住建筑為例，設計了3種不同的獎懲方案(S0、S1、S2)。當零能耗等級為1.0ZEB時，3種方案下的建筑總成本與常規總成本相比分別降低了50%、100%和50%。能耗等級從0.4BEC變化到2.0BEC時，3種方案下的總成本變化率區間分別為-124.5%～-24.8%、-250.3%～-49.8%、-182.3%～-24.8%，從而證明了通過引入獎懲函數可以對建筑總成本進行很好的調節，且其適用于能耗等級介于0.8BEC～1.8BEC的建筑。此外，當獎懲函數應用于不同的建筑能耗等級時，方案S1中的獎懲函數比方案S0和S2可應用的建筑能耗等級范圍更廣。

本文通過設計和證明引入的一元二次獎懲函數在建筑中的應用，旨在進一步推動零能耗建筑的發展。后續研究將從不同類型獎懲函數的設計和應用方面展開。