基于期望Sarsa 的進港航班排序模型研究

何愛平，張建偉，韓云祥

（1.四川大學視覺合成圖形圖像技術國防重點學科實驗室，成都610065；2.四川大學計算機學院，成都610065）

0 引言

2016 年我國機場旅客吞吐量突破1 億人次，完成飛機起降923.8 萬架次，2017 年我國機場旅客吞吐量達到11.48 億人次，起降架次達到1024.9 萬架次，旅客吞吐量、飛機起降架次逐年增長[1]。如此龐大的載運量使得我國的空域資源與交通流量沖突日益突出。機場終端區內一般具有多條航路交叉匯聚、空域狹窄、航班密度大、結構復雜、運行難度大等特點，嚴重影響到機場終端區的運行效率。為了盡量減少飛機因不必要的等待造成的延誤，前人提出了各種終端區流量管理手段，進場排序就是其中的一種，如何安全高效地指揮進港航班落地是一項意義重大的任務。

現有的進港航班排序算法大多為基于優先級的算法，如先到先服務算法（FCFS）[2]，同時還包括啟發式算法，如遺傳算法（GA）[3-4]、蟻群算法(ACO)[5]、粒子群算法（PSO）[6]、蒙特卡洛模擬[7]等。另外也有少數學者采用強化學習的研究方法進行了相關探索[8-9]。FCFS 雖然在一定程度上保證了航班進港排序的公平性，但該算法可能導致大面積的航班延誤等待，造成直接的經濟損失。這類啟發式算法雖然能夠搜索到較優的進港排序序列，但搜索的效率不佳，并且每次搜索得到的結果可能不同，最壞的情況下甚至需要對進港序列進行大幅度的調整，這不僅提高了管制難度，還增加了調整的開銷。強化學習屬于機器學習的分支，建立在馬爾科夫決策過程（MDP）假設之上，擅于解決序列決策問題，而確定進港序列可以抽象為該過程。現有的強化學習進港排序模型都是基于Q 學習算法和貪心策略的模型，由于Q 學習算法使用了貪心策略，可能會存在“過高估計”的問題，同時也缺乏未來狀態的預見性，而期望Sarsa 算法在策略上考慮了全部的歷史動作，訓練更加穩定。通過智能化的方法對進港航班實施排序，不僅能夠縮減延誤時間、保障旅客安全、提升管制效率，同時也極大地減少了經濟開銷和管制人力資源。

1 強化學習

強化學習啟發于行為主義心理學，是機器學習中產生的一種交互式學習方法的分支，用于解決一系列滿足MDP 條件的序列決策問題。MDP 描述了一個智能體（Agent）采取行動（Action）從而改變自身狀態（State）獲得獎勵（Reward），與環境（Environment）不斷發生交互的過程。強化學習的基本框架如圖1 所示。

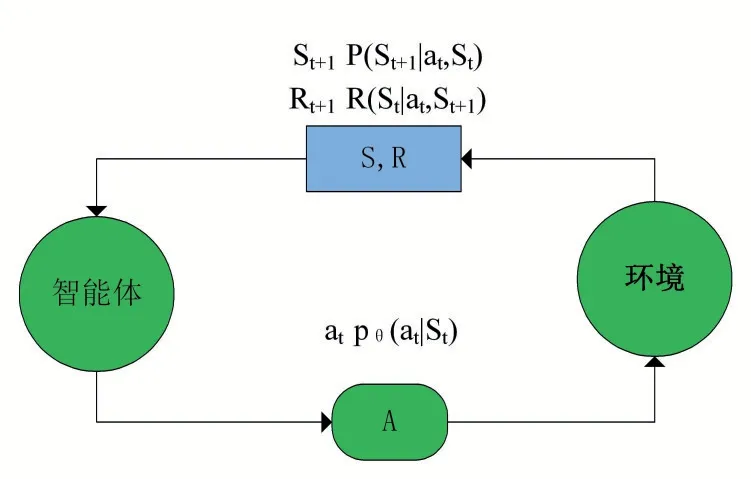
圖1 強化學習基本框架圖

強化學習的核心要素包括狀態集S、動作集A 和獎勵反饋R，用St表示t 時刻環境狀態集中某一狀態，At表示t 時刻Agent 采取的動作，At∈A，Rt表示t 時刻Agent 在狀態St采取的動作At對應的獎勵。MDP滿足馬爾科夫假設（Markov），即轉化到下一個狀態s'的概率僅與上一個狀態s 有關，與之前的狀態無關。MDP 可以用一個五元組來表示，定義了一個完備的強化學習模型：

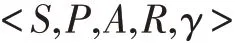
其中P 表示狀態轉移，定義了兩種狀態之間的轉移概率，γ 表示折扣系數（0 ≤γ ≤1），定義了未來獎勵的對當前狀態的重要程度。狀態轉移描述了從狀態s執行動作a，獲得獎勵r 并轉移到狀態s'的概率，用公式表示如下：

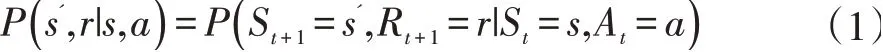
強化學習采用累積獎勵機制進行學習，為了評估Agent 所處環境以及采取對應動作的好壞，引入狀態值函數Vπ(s)和動作值函數Qπ(s,a)。值函數評估的指標為在相同策略下累計獎勵的期望值，采用期望的形式是由于累計獎賞函數為一個隨機變量，無法進行確定性描述。值函數的數學表達式如下：

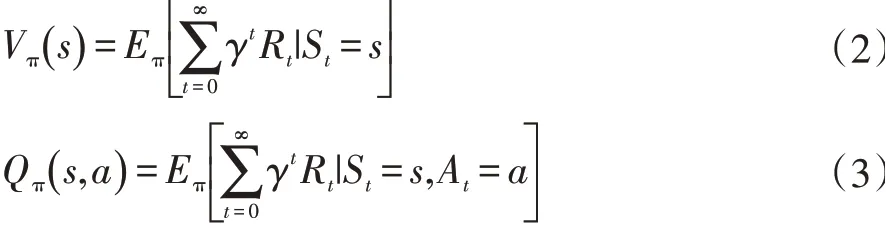
其中π 表示策略函數，定義了狀態到動作的映射關系。值函數統一遵循貝爾曼期望方程（Bellman Equation）的約束，通過該方程持續迭代優化到達策略最優的目的，如Q 學習的貝爾曼方程表示如下：

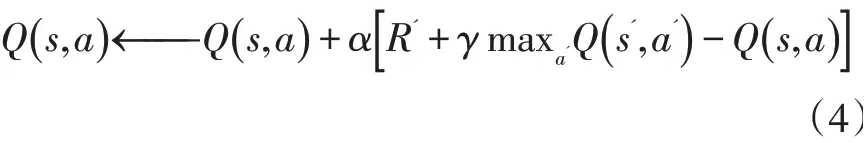
其中，R'表示下一時刻與環境交互獲得的獎勵值，α 為學習速率（0 ＜α ≤1）。在多數應用場景下，模型的狀態轉移矩陣是未知的，傳統的基于模型的學習方式無法解決問題，而免模型的學習方式可以直接從歷史的軌跡片段中學習，不需要了解模型的狀態轉移和完備的環境信息。時序差分算法（TD）是一種免模型算法，根據值函數更新策略和動作選取策略是否一致分為兩類：在線策略和離線策略，如Sarsa 算法為在線策略學習方式，而Q 學習算法為離線策略學習方式。

針對環境模型狀態、動作有限的問題，一般通過表格型強化學習方式進行建模，通過維護一個有限的狀態-動作Q 表，記錄每種狀態-動作對的Q 值，采用不同的更新策略結合公式（4）進行迭代學習，最終達到強化的目的。

2 進港航班排序模型

基于免模型的進港航班排序強化學習模型包括三個部分，環境與Agent 定義、狀態與動作設計、獎勵函數。另外，對比離線策略學習方式的Q 學習算法，采用在線策略學習方式的期望-Sarsa 算法進行建模。考慮相關約束條件并以延誤成本、延誤時間等因素為優化指標，建立強化學習模型對終端區進港航班排序。考慮安全因素方面，航空器在進行排序的過程中，必須滿足以下約束：

（1）尾流間隔。由于前機兩個翼尖處形成的兩個旋渦，后機若進入其中，容易誘導橫滾、損失高度、爬升率減小或增大等危險。國內采用的尾流間隔標準如表1 所示，一種為時間間隔（單位為分鐘），另一種方法為距離間隔（如海里）；

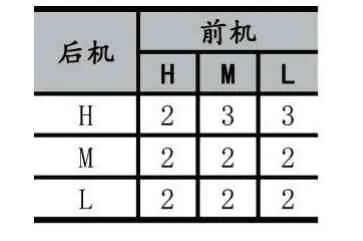
表1 國內尾流間隔標準（單位：min）

（2）同一進場航向上不允許超越。同一股交通流的航空器相互交換位置，叫做超越。管制員一般不愿意讓航空器進行超越，由于這種操作極易引發事故，并且需要花費大量時間和人力對該航空器進行監視和管控，但允許不同進場航向上的航班順序調換；

（3）為了減少強化學習模型中狀態維度的大小，設置航班的延誤上限為15 分鐘。

2.1 環境與Agent

進港排序Agent 為排序的核心主體，對終端區進港航班的序列進行調整，如實施延誤動作調整航班進港的時間，以達到整體序列延誤最小，且燃油消耗最少為目標進行優化。環境的組成基于真實的進港數據及其他約束條件，包括航班的ETA（預計到達時間）、尾流類型、機型等。終端區管制移交方式如圖2 所示，首先終端區的進港航空器會從不同的進場航段飛至IAF（起始進近定位點），完成進場任務，隨后由IAF 飛至IF（中間進近定位點），最后根據排序結果選擇相應的FAF（最終進近定位點），等待落地或者復飛，完成進近任務。

圖2 終端區管制移交方式

2.2 狀態與動作

強化學習中智能體的狀態描述了智能體可感知環境的一部分，合適的定義可加快智能體的學習速度，同時，狀態與動作設置的好壞直接影響了模型的性能。排序智能體的狀態空間定義為以ETA 為基準的提前或者延后15 分鐘范圍內的時間集合，動作空間定義為排序智能體給出的提前/延誤時間，用公式表示如下：

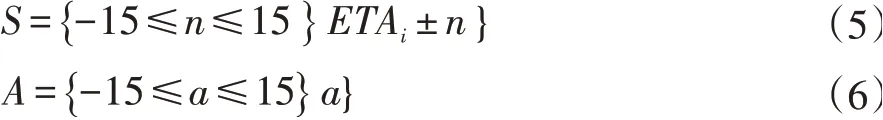
狀態集S 中，ETAi表示第i 架航空器的預計到達時間，即圖2 中的IAF 點，智能體根據設定的獎勵函數采取最佳的動作，用a 表示，即延誤/提前的時間（設定時間跨度為15 分鐘），n 表示設定的提前或延誤的分鐘數。

2.3 獎勵函數

強化學習航班進港排序的獎勵函數主要分為總延誤時間、經濟開銷、最晚落地時間獎勵項三個部分。原則上獎勵函數設計既要滿足計算盡可能簡單，又要滿足能全面評估智能體的學習指標這兩個條件，而對于航班進港排序最直接反映進港航班序列好壞的指標之一就是總延誤時間，其次為不同機型的航班因延誤而產生的經濟總開銷。另外，最晚落地時間指標表明了整體的進港時間長短，與總延誤時間不同的是最晚落地時間并不總是簡單地將總延誤時間進行加和，由于多個進場航向的存在，在時間上有重疊關系。依據上面的描述，將獎勵函數設計為如下的表達式：

其中，D 表示總延誤時間，C 表示總經濟開銷，T表示最晚落地時間的獎勵項，ρ、σ 與τ 為超參數，且滿足ρ+σ+τ=1，分別表示不同指標下的權重因子。各部分具體的定義如下，CTAi表示第i 架航班的排序落地時間，ηi表示該航班的燃油消耗經濟指標，具體定義在3.2 小節說明。最晚落地時間獎勵項對整體的進港時間進行獎勵，時間越短獎勵值越大。

2.4 期望Sarsa算法

Q 學習與期望Sarsa 算法的不同點在于行動策略與評估策略的異同，前者的行動策略和評估策略均采用貪婪算法，如在評估策略上每次選擇下一狀態的可選集中使得Q 值最大對應的動作，而后者考慮了下一狀態的整個可選集，將Q 值的期望作為目標值。期望Sarsa 的貝爾曼方程如下：

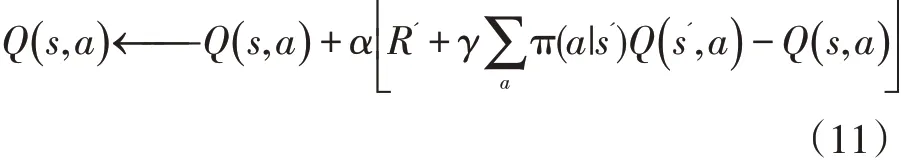
智能體的行動策略采用如下的公式進行選擇，即當前的動作若與貪婪算法選擇的動作一致，則以一定概率執行該動作，否則以設定的概率選擇非貪婪算法執行該動作。其中A 表示動作集的大小，A_greedy 表示采用當前動作與貪婪算法選擇的動作命中的次數，?表示貪婪度，即以貪婪算法作為行動策略的概率。

3 實驗結果分析

3.1 實驗平臺及數據來源

本實驗采用Python 3.6 實現，硬件平臺為Windows10×64 位系統，內存為24G，處理器為Intel Core i7-7700@3.6GHz CPU。實驗數據來源于flightradar24網站提供的真實進港數據，選取成都雙流機場2020 年10 月晚間高峰時段的20 架進港航班的數據。數據包括航班號、機型號、尾流類型、預計到達時間、后續航班、實際到達時間。

3.2 模型評價指標

宏觀上分析，根據《2019 年民航行業發展統計公報》[10]對不正常航班的分類統計結果顯示，導致航班延誤的主要因素為天氣原因，其次為航空公司的原因和其他原因，具體如表2 所示。

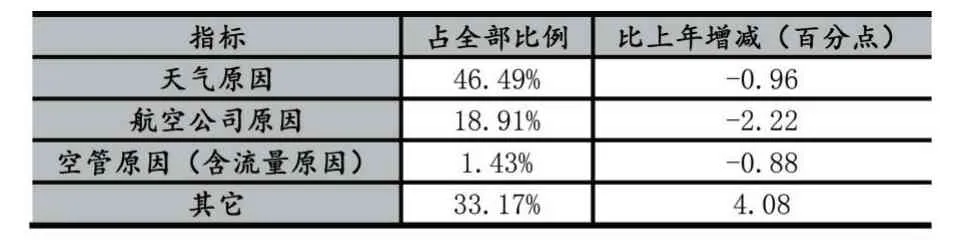
表2 2019 年航班不正常原因分類統計

從一個航班的完整運行過程上來分析，造成航班延誤的因素是多方面的，其中包括起飛前的關艙延誤、地面滑行延誤、空管起飛延誤、航路延誤、空管著陸等待延誤、流量控制延誤等[11]。進港航班排序模型的評價指標除了總延誤時間外，還應考慮這些延誤帶來的經濟開銷，而不同類型的航班在不同程度的延誤情況下產生的開銷也不同，因此精確計算延誤開銷尚存在困難。武喜萍等人[9]根據航班的類型確定延誤開銷水平，將重型機、中型機、輕型機的經濟開銷分別量化為4000元/小時、3000 元/小時、200 元/小時。楊晶妹[12]從機場容量方面考慮，將該時段降落航班的數量作為評估指標，即排序后最后一個航班的實際降落時間與第一個航班的降落時間差越小越好。

3.3 實驗結果分析

實驗主要對比了期望Sarsa 算法與強化學習算法，以及常規的啟發式算法。其中強化學習航班進港排序期望Sarsa 算法中的相關超參數設置如表3 所示。

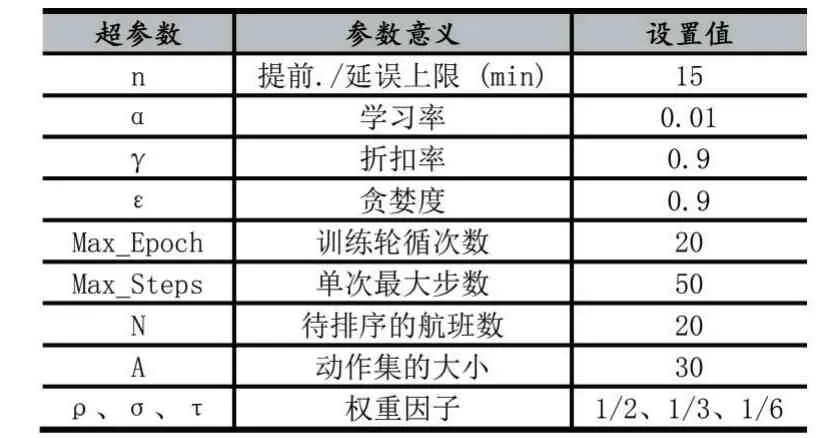
表3 期望Sarsa 模型超參數設置

以延誤時間、最晚落地時間、延誤開銷和運行時間作為比對指標進行實驗，得到不同啟發式算法與強化學習算法的對比結果如表4 所示。

表4 航空器進港排序算法結果對比

遺傳算法在進港航班排序上迭代優化的收斂情況如圖3 所示，在1180 代時算法模型已經收斂，目標函數最優值已到達0.78，對比其他算法計算得到的經濟開銷結果也表明遺傳算法在該指標上具有一定的優越性。

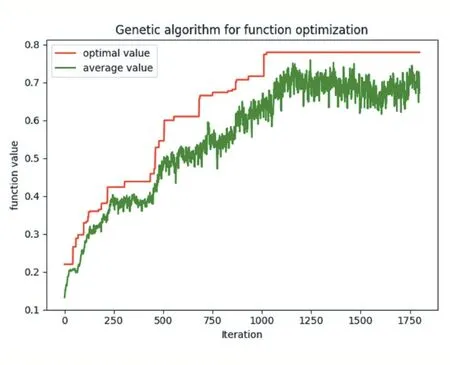
圖3 遺傳算法在航班進港排序上的迭代優化收斂結果

4 結語

本文給出了基于強化學習算法期望Sarsa 和Q 學習算法以及常用的啟發式算法在航空器進港排序應用上的效果對比，分別從總延誤時間、最晚落地時間、延誤經濟開銷以及程序運行時間四個維度進行對比。啟發式算法中，遺傳算法的運行時間最長但消耗的總經濟開銷最少。另外，先到先服務算法雖然運行時間最短，但經濟開銷較大。Q 學習算法在經濟開銷和運行時間上均表現較優，但在經濟指標上遜色于遺傳算法。對比Q 學習算法，期望Sarsa 算法由于其貝爾曼方程中的一個差分項需要計算后續狀態Q 值的期望值，計算量增加，導致該算法的運行時間較長，但得到的排序結果在經濟開銷上優于Q 學習算法，在一定程度上證實了期望Sarsa 算法的性能優于采用最優Q 值的Q學習算法[13]。