基于稀疏自編碼器和高斯混合模型的手寫數據集分類

馬雙寶，高夢圓，胡江宇，賈樹林，董玉婕

(武漢紡織大學 機械工程與自動化學院，湖北 武漢 430200)

深度學習是當今較為火熱的領域之一。對于大量的樣本進行學習，深度學習網絡比其他的機器學習算法表現結果更為出色，但是現實生活當中并沒有大量的標簽數據。人類可以對新的事物只需要觀察一次，在下次出現時就可以清楚地進行辨認。因此在處理小樣本問題，李飛飛等人[1]在2006 年提出了one-shot問題，并且利用了貝葉斯推測方法對小樣本進行分類，并取得較好成績，成為小樣本學習的開端。C. Finn,P. Abbeel 等人[2]根據元學習模型，提出了MAML 算法，根據訓練不同得到的先驗知識來指導新的任務，該模型取得不錯的泛化能力，但是該模型需要預先訓練，對參數調節具有一定要求。Oriol Vinyals 等人[3]提出了匹配網絡對數據進行聚類分析，該網絡可以對多個類別進行判別。Pake Snel 等人[4]提出了基于原型網絡的聚類算法，它是通過新數據對原型網絡的距離來衡量數據的類別的一種聚類算法。該算法只是通過簡單的歐式距離作為聚類的標準，對于有些樣本來說，泛化能力較差。Sachin Ravi 等人提出了基于優化的模型采用LSTM 來對小樣本問題進行優化求解，但是模型復雜度過高，對樣本存在過擬合問題。

上述方法均沒有對樣本的維度進行降維處理，小樣本數據進行特征提取，由于維度過高會導致過擬合問題，而且維度過高對計算帶來巨大運算問題。針對上述問題，本文采用一種基于稀疏編碼器降維算法，首先對數據進行低維壓縮處理，防止樣本數量過少導致過擬合問題，然后利用高斯混合模型對數據進行聚類分析。

1 相關模型

1.1 稀疏自編碼器模型

傳統的降維算法主要采用主成分分析法對數據進行降維處理。主成分分析法采用將線性相關的一些變量通過正交變換轉化成為一組少量的線性無關的變量表示。該算法屬于一種線性變換，但是現實生活當中的數據往往呈現非線性關系，因此降維后的效果往往不是很好。

本文采用自編碼網絡進行數據維度的自動壓縮。自編碼器是一種神經網絡模型，該網絡可以自動進行特征提取，不需要人為進行特征運算。自編碼器是一種無監督學習方法，因此采用該網絡對標簽有無沒有關系，它通過輸入和輸出的損失作為損失函數進行反向傳播，是一種非線性的降維方法。在一定層度上能夠保證輸入和輸出的大部分信息完整并且具有較強的泛化能力。

圖1 采用PCA 將維度降低到20 圖像

圖2 采用中間層維度為20 圖像

圖3 采用中間隱藏層為16 圖像

如圖1-3 所示為采用PCA 降維算法和自編碼器算法進行數據降維效果，從圖中可以看出，將原始圖像的特征維度同樣壓縮至20，采用PCA 算法進行圖像復原，有些圖片出現模糊，而采用自編碼圖片依然可以清晰看見。因此采用自編碼器對數據降維效果好于PCA 算法。

自編碼器由兩部分組成：編碼器和解碼器。編碼器對數據進行降維處理，編碼器對數據進行重塑。中間隱藏層為我們需要進行降維處理的數據維度（見圖4）。

為了在數據降維過程當中提取較好的特征，我們在損失函數中添加正則項增減網絡的稀疏性（見圖5-圖8）。

圖4 自編碼器網絡工作原理圖

圖5 隱藏層為32 的普通編碼器損失曲線

圖6 隱藏層為16 的稀疏自編碼器損失曲線

圖7 中間隱藏層為32 的普通編碼器精度曲線

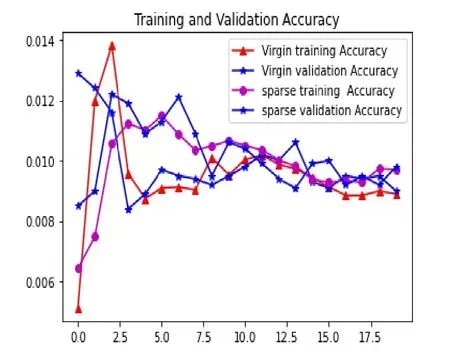
圖8 中間隱藏層為16 的稀疏自編碼器精度曲線

從圖5-圖8 中可以看出，采用稀疏編碼器的網絡首先較快，而未采用稀疏編碼器的網絡收斂較慢，普通自編碼器的網絡過擬合比較嚴重。因此，我們采用稀疏編碼器對原始數據進行降維處理。

圖9 稀疏編碼器中間隱藏層為2 原始圖像與重建圖像

圖10 普通自編碼器中間隱藏層為2 原始圖像與重建圖像

現在將中間隱藏層的維度降低為2，這樣直接可以對數據進行可視化操作，但是將中間隱藏層的維度設置為2 時，經過解碼器后圖像變得比較模糊（見圖9-圖10），顯然直接將中間隱藏層的神經元個數設置為2 不可行。首先將中間神經元個數設定某一值，讓后再繼續利用降維方法將維度繼續降低。

1.2 T-SNE 算法

T-SNE 算法(t-distributed stochastic neighbor embedding,T-SNE)是一種無監督的降維算法。 T-SNE 算法能夠有效對高位數據進行非線性降維。

假設n 維空間數據點{x1，x2,…,xN}，則數據e 間的兩兩相似條件概率為：

利用梯度下降法對KL 進行迭代求解得到原始數據經過降維后的數據。圖11 為利用T-SNE 算法將數據維度降為2 的圖像。

圖11 利用T-SNE 算法將數據維度降為2 的圖像

1.3 基于高斯混合模型原型聚類

經過T-SNE 算法將高位數據降維到2 維空間，現在需要對數據進行分析。

聚類算法屬于無監督學習方法，該算法不需要對樣本進行標記，通過數據的內在規律，對數據進行自動歸類的一種算法。

Pake Snell 等人[4]利用基于原型的聚類算法對數據進行處理。該算法需要從數據集當中找一組初始化的原型向量，通過新數據與原型向量間的距離度量，找到離樣本距離最近原型向量來進行類別劃分。該算法性能好壞主要取決于原型向量選取與樣本距離度量方式的選擇。

其中Sk表示第k 個類別的樣本數目，f?表示映射函數，ck表示原型。

公式（6）代表利用映射函數f?，將輸入數據xi轉換為特征向量，然后通過幾組特征向量加和求均值得到原型向量ck。

然后利用原型向量與新樣本之間的歐式距離來度量樣本的相似性。新的樣本通過距離原型向量距離最小來劃分到該原型網絡的類別。該算法性能好壞取決于原型向量的選取。而且樣本之間距離的度量采用歐式距離并不能準確表示樣本差距，因此本文采用基于高斯混合模型的聚類方法。

高斯混合模型以概率為基礎進行原型聚類，是典型的生成式模型。高斯混合模型采用多個多元高斯混合分布來估計樣本的概率分布。

公式（8）表示多元高斯分布，其中μ，∑表示高斯分布的均值和協方差。

采用k 個類別的多元高斯混合分布來進行數據的概率密度估計。其定義的分布為：

其中，μi，∑i表示第 i個高斯分布的期望與協方差，αi表示取得第i個混合成分的概率。

高斯混合模型是典型的生成概率模型：首先根據αi選擇第i個混合成分，讓后根據相應混合成份來生成數據。設樣本xj在k 個族中劃分的標記為λj。采用高斯混合模型進行聚類時，我們進行優化求解采用最大后驗概率，即給定樣本xj是第i個混合成分生成的后驗概率γij的最大化。

由于等式當中含有隱變量αi，因此采用EM 算法進行求解。該算法分兩步：E-Setp，求期望；M-step，計算新一輪的模型參數估計值。重復E-Step 和M-Step 直到模型收斂。

E-Step：依據當前的參數，計算每個j數據來自子模型k 的可能性。

通過不斷更新E-Step 和M-Step，最終得到收斂，求解極大后驗概率值。

2 仿真實驗與分析

本文首先采用稀疏自編碼器對數據進行降維處理，由于將中間隱藏層維度設置為2，經過解碼器圖像已經變得模糊，采用T-SNE 算法對中間隱藏層維度繼續進行降維處理得到二維圖像。采用高斯混合模型對二維數據進行極大后驗概率估計，由于含有隱變量，采用EM 算法進行迭代求解，最后得到聚類結果。在稀疏編碼器設計輸入數據的維度為128，全連接層有兩層，維度分別為64 和16，解碼器和編碼器結構對稱。為了增加自編碼器的稀疏性，在中間隱藏層加入L1 正則化。正則化會使很多隱藏層神經元權重變為0，使得神經元變得稀疏。采用交叉熵作為損失函數來作為輸入數據和輸出數據的損失函數。采用Adam 作為優化器，每次喂入神經元數據為128，迭代50 次。在經過T-SNE 算法和高斯混合模型時，類別個數設置為10。本文采用的數據集為mnist 手寫數據集，該數據集公共有60000 張測試圖片和10000 張訓練圖片，每張圖片的大小為28*28。

為了進一步探討，采用卷積神經網絡對手寫數據集進行分類。

3 實驗結果與分析

利用上述方法對手寫數據集進行聚類結果如圖12-圖15 所示。圖16 和圖17 為稀疏自編碼器損失曲線和精確度曲線。在訓練集訓練精度為0.89025，在測試集的訓練精度為0.896。從圖16 和圖17 中可以看出，采用稀疏編碼器的損失曲線和精確度曲線差別不大，對數據進行降維處理在一定程度上防止了數據的過擬合。

圖12 手寫數字0 聚類

圖13 手寫數字1 聚類

圖14 手寫數字2 聚類

圖15 數字3 聚類結果

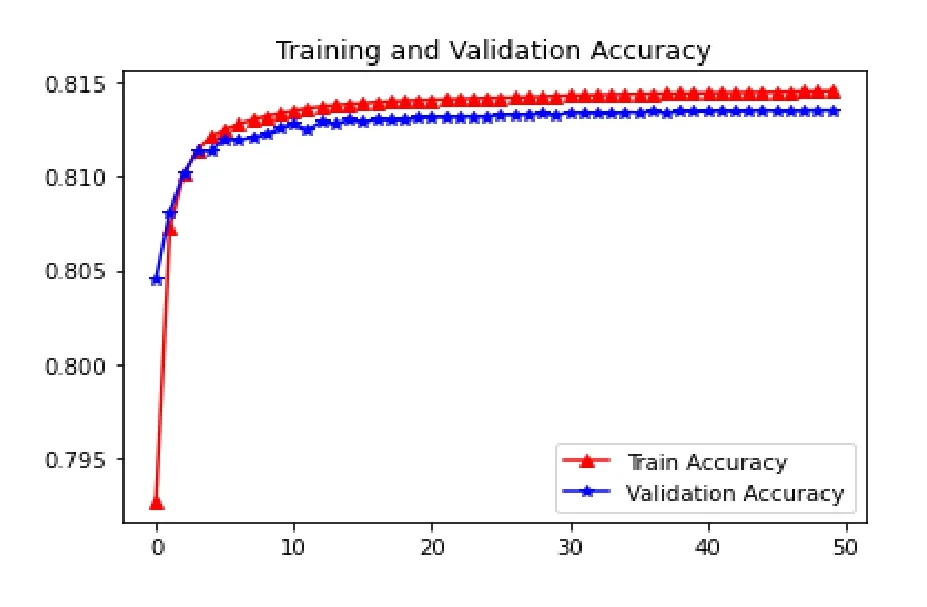
圖17 稀疏自編碼器網絡準確度曲線

圖18 采用卷積神經網絡損失曲線

從圖16-圖19 中可以看出，采用卷進神經網絡在訓練集和測試集合出現過擬合，而采用稀疏自編碼器網路訓練集和測試集曲線能夠很好擬合。本文采用的稀疏自編碼器網絡對數據降維，和高斯混合模型對數據集進行聚類均為無監督學習算法，因此不需要預先知道樣本的標簽，具有較好的自適應能力。但是，在精度上，采用卷積神經網絡優于本文算法。

4 總結

本文采用稀疏編碼器對數據進行降維處理，中間隱藏層維度設置為2，對數據進行可視化，然后再利用解碼器進行圖像解碼，但圖像模糊。因此直接中間隱藏層神經元個數設置為2 不合適，需要進一步進行降維。考慮到本文采用無監督算法，因此采用T-SNE 算法對中間隱藏層數據進行降維處理。然后采用高斯混合模型對數據進行降維處理。在整個算法的過程當中，都是無監督學習，因此不需要數據對應的標簽，減少了人工成本。本文算法不足之處在于并非一種完全端到端學習。在對小樣本學習探索中，缺乏對多個類別小樣本的探索。在精度方面低于卷積神經網絡，需要對模型進行優化，進一步提高精度。