稀疏表示系數下局部最優重構的SAR圖像目標識別算法

唐吉深，覃少華

(1.河池學院，廣西 河池 546300;2.廣西多源信息挖掘與安全重點實驗室，廣西 桂林 541004;3.廣西師范大學計算機科學與信息工程學院，廣西 桂林 541004)

0 引言

自20世紀90年代以來，合成孔徑雷達(synthetic aperture radar, SAR)圖像目標識別問題在世界范圍內得到廣泛研究并產出了大量的成果[1-2]。SAR目標識別系統通過檢測、鑒別和分類的三個階段從大場景圖像中獲取感興趣的目標并判定其類別。現有公開的SAR目標識別算法主要集中在對分類算法的研究，即在已經剔除虛警后的感興趣目標區域(region of interest，ROI)的基礎上對其類別進行決策(后文將其稱為SAR目標識別)。一般的SAR目標識別算法主要設計特征提取和分類決策兩個環節。前者通過分析目標幾何形狀、灰度分布以及電磁散射等特點獲取低維特征矢量，實現對目標核心特性的有效描述。文獻[3—5]以目標區域、輪廓等為基本特征設計SAR目標識別算法。文獻[6—9]采用主成分分析(principal component analysis，PCA)、非負矩陣分解(non-negative matrix factorization，NMF)、單演信號分解等手段獲取SAR圖像的不變特征。文獻[10—11]基于屬性散射中心設計SAR目標識別方法，通過散射中心的一一配對考察目標可能出現的局部變化。分類決策階段，根據提取特征的不同規律和特點，選用相適應的分類機制。目前，在SAR目標識別中廣泛運用的分類器包括K近鄰(K-NN)[6]、支持向量機(support vector machine，SVM)[12]、稀疏表示分類(sparse representation-based classification，SRC)[13]以及深度網絡[14-15]等。

稀疏表示目前已在模式識別領域獲得到廣泛運用。Wright等人[16]首次將稀疏表示運用于人臉識別并根據各訓練類別的重構誤差進行決策；Thiagaraianm等人[13]將稀疏表示分類引入SAR目標識別；后續，稀疏表示分類成為SAR目標識別中廣泛運用的分類器之一，對于多種特征均有良好的適應性。這些算法多是基于最小重構誤差準則進行分類決策。文獻[17]提出基于最大系數能量的決策方法，其基本思想是計算各個類別上系數的能量和，根據最大能量的準則進行決策。無論是最小重構誤差準則還是最大系數能量準則，它們的應用并沒有深入分析SAR目標識別這一問題的特殊性。與光學圖像不同的是，SAR目標圖像對于方位角變化具有很強的敏感性[18]。因此，在稀疏表示過程中，只有與測試樣本具有相近方位角訓練樣本才是有效的，其余樣本的引入容易造成更大的誤差。文獻[19]正是利用SAR圖像的方位角敏感性設計了方位角區間內的稀疏表示方法(SRCA)并應用于目標識別。本文針對當前相關研究存在的問題提出全局稀疏表示系數下局部最優重構的SAR目標識別方法。

1 稀疏表示分類

稀疏表示的基本思想是采用預先構建的字典對特性位置的樣本進行稀疏重構，從而根據表示稀疏的分布規律對未知樣本的特性進行有效評估。具體在目標分類鄰域，字典一般由類別確定的訓練樣本構建然后對待分類的測試樣本進行表示。假設D=[D1,D2,…,DC]∈Rd×N為來自C個類別的全局字典，其中Di為來自第i類別的Ni個訓練樣本，對測試樣本y的稀疏表示過程可描述如下：

(1)

式(1)中，x為待求解的稀疏表示系數矢量，ε為重構誤差的約束門限。式(1)中的優化問題難以直接求解。為此，研究人員通過1范數等效[16]或貪婪算法(如正交匹配追蹤算法(orthogonal matching pursuit，OMP))[13]獲得近似解。

在獲得稀疏表示系數的基礎上，按照式(2)計算各個類別對于測試樣本的重構誤差。

(2)

式(2)中，xi為對應于第i類的系數；r(i)為相應的重構誤差。

傳統的稀疏表示分類大多根據重構誤差的大小進行類別判定，即具有最小重構誤差的訓練類別為測試樣本的目標類別。后續，也有研究人員根據各類別系數能量的大小作為判決依據。需要指出的是，這些方法都在所有非零表示系數上進行決策，缺乏對獨立原子的考察。實際上，由于SAR圖像自身具有的特性，對稀疏表示系數進行更深層次考察和分析有利于獲得更為準確的分類結果。

2 局部最優重構的目標識別算法

2.1 SAR圖像方位角敏感性

SAR圖像具有較強的方位角敏感性，即當目標和雷達平臺的方位向視角變化較大時，圖像中的目標特性表現出很大的差異。這一特性導致了同一目標的不同方位角SAR圖像之間的差異往往超過了不同類別之間的某些圖像差異，給識別問題帶來較大的混淆。同時，在多視角樣本可利用的條件下，方位角敏感性又為多視角識別方法提供了更充分的信息。不同視角之間相互補充從而為目標類別的確認提供了更強的鑒別力，文獻[20—22]正是基于此設計了多種多視角SAR目標識別方法。

傳統基于稀疏表示的SAR目標識別方法的決策思路與光學圖像識別一致，并沒有考慮到SAR圖像的方位角敏感性。實際上，對于SAR圖像測試樣本，與其高度相關的原子(無論是來自正確類別還是錯誤類別)應當與其具有相近的方位角。因此，針對SAR目標識別的稀疏表示系數應該具有明顯的方位角區間特性。這一特性的引入有利于進一步增強稀疏表示系數以及重構誤差區分不同類別的能力，從而提高目標識別性能。

2.2 基于局部最優重構目標識別方法

本文在全局稀疏表示的基礎上提出局部最優重構方法。本方法通過SAR圖像方位角敏感性的引入進一步考察各訓練類別對于測試樣本的真實表征能力。對于全局字典，按照方位角升序的方式對其中各個類別的訓練樣本分別進行排列。對于求解的稀疏表示系數矢量，選取其中P個最大的系數，記為x(P)。這一步的目的主要是剔除大量無關原子(即與測試樣本的方位角差異很大)的影響。根據選取的原子及其對應的系數，分別在各個類別上對測試樣本進行重構：

(3)

saz(i)=var([k1,k2,…,kMi])

(4)

式(4)中，函數var()計算方差。當選取原子之間聚集性較差時，方差相對較大；反之，方差相對較小。據此對式(3)中的重構誤差進行加權修正，得到最終的決策變量如下：

dv(i)=exp(saz(i))·rL(i)

(5)

式(5)計算得到的決策變量與重構誤差具有一致的含義。通過方位角聚集系數的引入使得最終的決策變量更具可靠性。分類階段，根據式(5)計算的各類別對應的決策變量，采用最小誤差原則進行目標識別。因此，相比于傳統的全局稀疏表示，本文方法的目標是在局部字典上通過利用方位角的敏感性獲得最優重構，并通過分析稀疏系數的分布規律進一步突出真實類別與虛假類別之間的差異，從而提升最終的識別性能。

本文主要是在傳統稀疏表示的基礎上針對SAR目標圖像的特性進行改進，設計了更適用于SAR目標識別的新方法。圖1為提出方法的基本流程。對于測試樣本，首先在全局字典上對其進行稀疏表示，獲取系數矢量；根據當前識別問題的規模(待識別的類別數量)選取少量的最大系數并在各個類別上對測試樣本進行重構；最后，按照式(4)計算各類別上系數的方位角聚集系數并對重構誤差進行修正，獲取最終的決策矢量進行目標識別。方法的具體實施中，從全局稀疏表示系數中選取P=5C個最大系數；采用經典的PCA對測試和訓練樣本進行特征提取，從而降低計算復雜度。

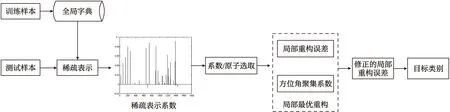
圖1 方位角敏感性約束下局部最優重構的SAR目標識別方法流程Fig.1 Procedure of SAR target recognition based on local optimal reconstruction under the constraint of azimuthal sensitivity

3 實驗與分析

3.1 MSTAR數據集

為驗證提出方法的有效性，基于MSTAR數據集開展實驗。該數據集中包含如圖2所示的10類車輛目標，各類目標圖像由X波段SAR傳感器采集，成像模式為聚束模式，分辨率0.3 m。對于任一類目標，其SAR圖像樣本的相鄰方位角間隔約為1°～2°。現階段，大多數公開文獻中的SAR目標識別算法均是基于MSTAR數據集進行性能測試，表明其權威性。

標準操作條件(standard operating condition)和擴展操作條件(extended operating condition)是SAR目標識別中兩類情形。標準操作條件指的是當前測試樣本與構建的訓練(模板)樣本差距較小，可近似認為采集自相同的條件。反之，擴展操作條件則是指由于測量條件(包括背景環境、目標自身、傳感器等因素)的變化，測試樣本與訓練樣本存在較大的差異。典型的擴展操作條件包括型號變化、俯仰角變換、噪聲干擾等。為了充分驗證提出方法的性能，本文在后續實驗中分別在標準操作條件和部分擴展操作條件下對其進行測試。同時，選用若干對比方法進行同步測試，分別為文獻[13]中基于最小重構誤差分類原則的SRC方法(記為“最小誤差-SRC”)，文獻[17]中基于最大系數能量的SRC方法(基于 “最大能量-SRC”)，文獻[19]中基于SRCA的方法，文獻[12]基于SVM的方法以及文獻[14]中基于全卷積神經網絡(A-ConvNets)的方法。其中，前兩個對比方法與本文方法一樣，采用SRC作為基礎分類器，但其具體的決策準則與本文不同。

圖2 10類目標的光學圖像Fig.2 Optical images of the ten targets

3.2 標準操作條件

標準操作條件下的識別問題相對簡單，但它是對SAR目標識別算法的基本考核。表1給出了當前基于MSTAR數據集設置的一種典型標準操作條件，包含了其中全部10類目標。其中，訓練和測試樣本來自相同的目標型號，唯一的區別為2°的俯仰角差異(兩者分別來自17°和15°俯仰角)。圖3顯示了提出方法在標準操作條件下的分類結果，各類目標的正確識別率如對角線所列，綜合得到10類目標的平均識別率為98.74%。

表2對比了各類方法在標準操作條件下的識別性能。在識別精度方面，本文方法的平均識別率略低于A-ConvNets方法而優于其他方法。在標準操作條件下，訓練樣本與測試樣本相似高，能夠較好覆蓋測試樣本中出現中的各種情形。因此，訓練得到的卷積神經網絡分類能力很強，能夠取得很高的識別率。與其他三類基于SRC的方法相比，本文方法的識別率有一定的提高，表明通過局部最優重構能夠有效改善識別性能。方位角約束下的SRCA方法相比最小誤差-SRC和最大能量-SRC具有更高的識別率，表明充分利用SAR圖像的方位角敏感性有利于提升整體識別性能。在相同的硬件平臺上對各類方法進行測試并計算它們識別單個測試樣本所需的時間消耗。從表中可以看出，本文方法的效率低于最小誤差-SRC和最大能量-SRC方法但高于其他方法。由于本文方法在決策變量的計算中充分考慮了稀疏系數矢量的局部特性因此相比簡單最小重構誤差和最大系數能量需要更多的時間消耗。對于SVM和A-ConvNets方法，它們則需要分類器的訓練時間。綜合來看，本文方法在標準操作條件下的性能較優，能夠較好地完成多類目標的識別任務。

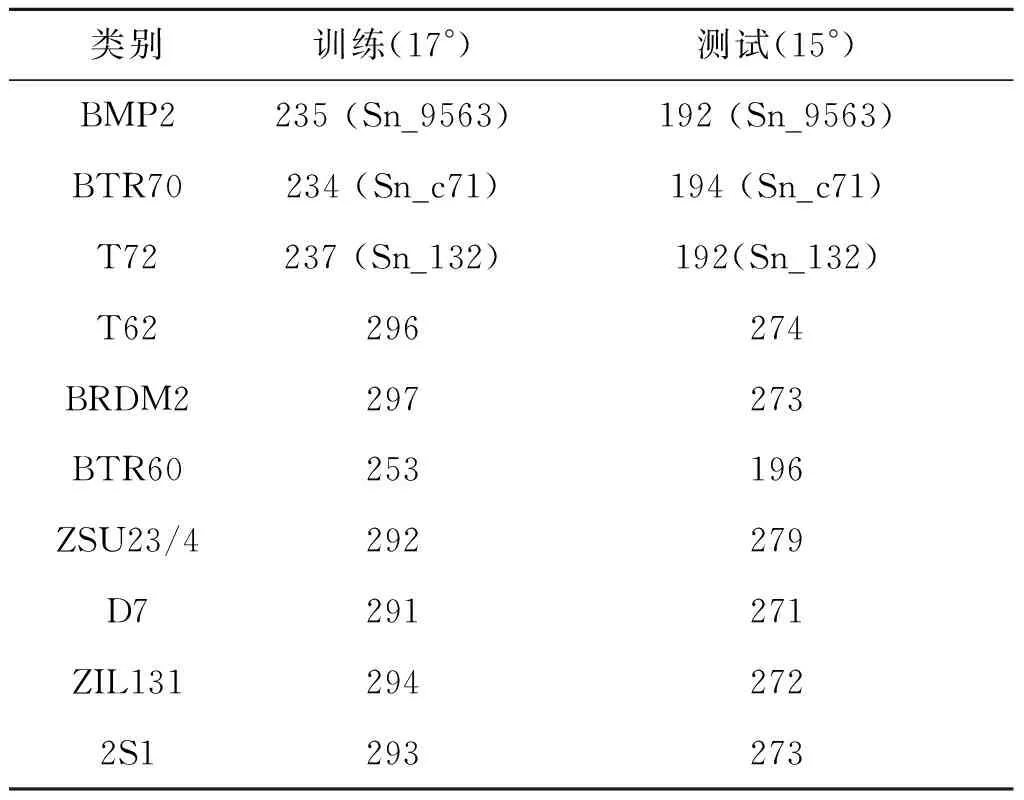
表1 標準操作條件的典型實驗設置Tab.1 Typical experimental setup under SOC

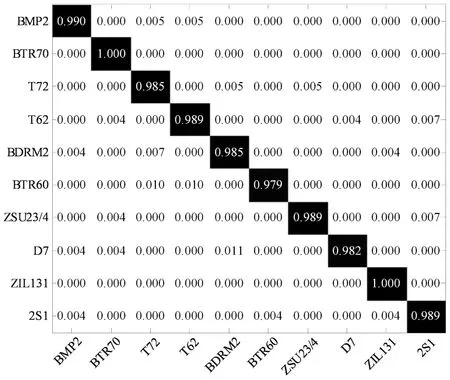
圖3 本文方法在標準操作條件下的分類結果Fig.3 Classification results of the proposed method under SOC

表2 各方法標準操作條件下的性能比較Tab.2 Performance comparison of different methods under SOC

3.3 擴展操作條件

3.3.1 型號變化

目標自身型號變化時SAR目標識別中一種典型擴展操作條件，主要是指測試樣本的目標型號與訓練樣本存在差異。表3給出了基于MSTAR數據集設置的型號變化條件下的訓練和測試集。其中，BMP2和T72的測試型號與訓練樣本完全不同；BTR70的引入主要是為了進一步增加識別問題的難度。表4對比了各類方法在型號變化條件下的平均識別率，本文方法性能最優。當訓練樣本與測試樣本存在一定差異時，訓練得到的卷積神經網絡分類性能出現下降，這也是當前基于深度學習方法的方法對于大量訓練樣本的依賴性。與其余兩類SRC方法相比，本文方法在型號變化條件下仍然能進一步提高識別穩定性，表明了設計的局部最優重構算法的有效性。

表3 型號變化下的典型實驗設置Tab.3 Typical experimental setup under configruation differences

表4 各方法型號變化下的平均識別率Tab.4 Average recogntion rates of differnet methods under configuration differences

3.3.2 俯仰角變化

隨著訓練和測試樣本俯仰角差距的不斷增大，識別問題也不再是標準操作條件。由于較大俯仰角差異帶來的SAR圖像差異使得識別問題尤為困難。基于MSTAR數據集設置如表5所示的訓練和測試集，3類目標以17°俯仰角下的圖像作為訓練集分別對30°和45°俯仰角下的測試樣本進行分類。各類方法在不同俯仰角的平均識別率如圖4所示。顯然，由于俯仰角差異相對較小，30°下的識別性能遠遠優于45°下的性能，主要是因為28°的大幅俯仰角變化使得測試樣本和訓練樣本出現了很大的差異。對比各類方法，本文方法在兩個角度下都取得了最佳的性能，驗證其對于俯仰角差異的穩健性。在俯仰角變化較大的情況下，可用于表征測試樣本的訓練樣本不斷減少。因此，通過選取合適的訓練樣本進行最優重構有利于避免無效樣本的影響從而提高決策的可靠性。

表5 俯仰角變化下的典型實驗設置Tab.5 Typical experimental setup under depression angle differences

圖4 各方法在不同俯仰角下的平均識別率Fig.4 Average recognition rates of different methods at different depression angles

3.3.3 噪聲干擾

噪聲伴隨著SAR數據采集以及成像的整個過程。盡管現階段已經有了一些SAR圖像噪聲抑制算法，但噪聲仍然是影響SAR目標識別性能的重要因素。原始MSTAR數據集信噪比(signal-to-noise ratio，SNR)較高，難以直接考察目標識別算法在低噪聲水平下的性能。為此，本文首先按照文獻[10]中的策略向表1中的訓練樣本添加噪聲，然后基于構造的噪聲樣本測試各方法在噪聲干擾條件下的分類性能。圖5為各類方法在不同信噪比下的識別率曲線。顯然， 噪聲水平的不斷提高導致各類方法的識別性能均出現了明顯的下降。對比可見，本文方法對于噪聲干擾具有更強的穩健性。此外，基于SRC的四類方法對于噪聲干擾表現出更好的適應性，尤其在低信噪比的條件下，性能優勢更強，這與文獻[16]中的實驗結果具有一致性。對于A-ConvNets方法，受噪聲干擾影響，基于高信噪比(原始)訓練樣本訓練的網絡對于低信噪比的SAR圖像的適應性較差。

圖5 各方法在噪聲干擾下的平均識別率Fig.5 Average recognition rates of different methods under noise corruption

3.4 方位角間隔大小影響

在局部重構中，按照升序排列的相鄰原子方位角間隔對算法性能存在影響。采用原始MSTAR數據集時，相鄰原子方位角間隔約為1°～2°，此時兩幅SAR圖像具有較高的相似性。隨著這一間隔的增大，相鄰圖像的相關性降低，會一定程度破壞稀疏系數的局部聚集性規律。為此，本實驗在原始局部字典的基礎上通過去除部分原子的思路，考察方位角間隔的影響。具體的，在基于表1設置的實驗條件下，對局部字典中的原子進行抽樣，并統計識別結果如表6所示。其中，“隔1取1”表示在原始局部字典中間隔1個保留下1個，去除中間的原則，其余條件同理。從結果可以看出，隨著方位角間隔的不斷增大，各類方法的性能均出現下降。對于幾類對比方法，它們性能下降主要是由于可用訓練樣本的規模減小，導致分類器的可靠性下降。本文方法除了上述原因外，還存在大方位角間隔條件下局部原子結構的破壞，導致性能下降。總體來看，本文方法在“隔1取1”和“隔3取1”兩種條件下還可以保持最高識別率，但在“隔5取1”條件下性能不再是最優。這樣反映了方位角間隔增大對所提方法的影響。

表6 各方法在方位角間隔變化條件下的平均識別率Tab.6 Average recogntion rates of differnet methods under variation of azimuthal interval

4 結論

本文提出稀疏表示下局部最優重構的SAR目標識別算法。該算法通過在全局字典上求解得到的稀疏表示系數選取若干最大的系數；然后，根據選取的系數分別在各個訓練類別上對于測試樣本進行重構；同時，根據SAR圖像的方位角敏感性對各類別上的系數結構進行分析，并與各類別的重構誤差進行結合，獲得最終的決策變量完成目標識別。實驗結果表明，該方法在標準操作條件和擴展操作條件下均可以取得更好的性能。