基于LADRC的四旋翼飛行器抗風擾控制
朱二琳 趙俊杰


摘? ? 要:對風干擾下的四旋翼飛行器軌跡跟蹤控制問題進行研究。在建模過程中考慮風力的作用,針對飛行器位置回路和姿態回路,分別設計線性自抗擾控制器(LADRC),構成雙閉環控制系統。將模型內部的擾動和外部風的干擾看作系統總的擾動,通過LADRC的擴張狀態觀測器(ESO)進行觀測,在控制律中予以補償,同時,還可消除位置通道和姿態通道之間的耦合。根據常值陣風和正弦陣風的干擾對模型和控制器進行仿真,將控制性能同現有的控制算法進行對比,結果驗證了方法的有效性和魯棒性。
關鍵詞: 四旋翼;軌跡跟蹤控制;LADRC;風擾
中圖分類號:V249.1? ? ? ? ? ? ? ?文獻標識碼:A? ? ? ? ? ? ? 文章編號:2095-7394(2021)02-0016-09
旋翼飛行器具有對稱分布的兩組螺旋槳,每組螺旋槳相對運動,產生的陀螺效應可相互抵消。通過改變四個旋翼的轉速不僅能控制飛行器的飛行姿態,還可以實現垂直升降和定點懸停,顯示了良好的可操縱性。因此,憑借結構簡單、易于操作等優點,當前四旋翼飛行器已廣泛應用于民用和軍用領域[1-2]。
同時,四旋翼飛行器作為一類欠驅動的系統(6個自由度,4個控制輸入),具有高度的非線性和強耦合性,易受到外界的干擾,從而增大了控制難度。目前,對于四旋翼飛行器的控制主要有以下幾種方法:ZHOU F等[3]、LEE D等[4]采用反饋線性化控制;ASHFAQ A等[5]、趙元偉等[6]、滕雄等[7]采用反步法控制,依賴于高精度的數學模型,但該方法不適用于復雜度較高或含有不確定項的模型;竇立謙等[8]將反步法與觀測器結合,使擾動的影響得到了改善,但控制器形式較為復雜,不利于工程實現;RONG X等[9]、陳增強等[10]、ABCI B等[11]對四旋翼姿態的滑模控制做了一定的工作,但結果容易出現抖振,不利于系統穩定性;葉孝璐等[12]、李杰等[13]、楊立本等[14]將自抗擾控制(Active Disturbance Rejection Control,ADRC)應用到了四旋翼,葉孝璐等研究了四旋翼的串級ADRC懸停控制,李杰等、楊立本等研究了四旋翼的ADRC姿態解耦控制,但對于陣風的干擾缺少相關討論。
本文主要對陣風干擾下四旋翼飛行器的軌跡跟蹤控制進行研究,將陣風對飛行器的影響視為作用于飛行器的力,在運動方程中予以體現。控制系統分為位置回路和姿態回路,分別設計線性自抗擾(Linear Active Disturbance Rejection Control, LADRC)控制器,通過線性的擴張狀態觀測器將陣風對四旋翼的干擾進行實時觀測,利用狀態反饋進行消除;同時,對于建模中的不確定因素也可有效消除。仿真結果表明:此方法可有效消除陣風對四旋翼飛行器的干擾,且易于實現。
1? ? 四旋翼飛行器動力學模型
1.1? 相關坐標系
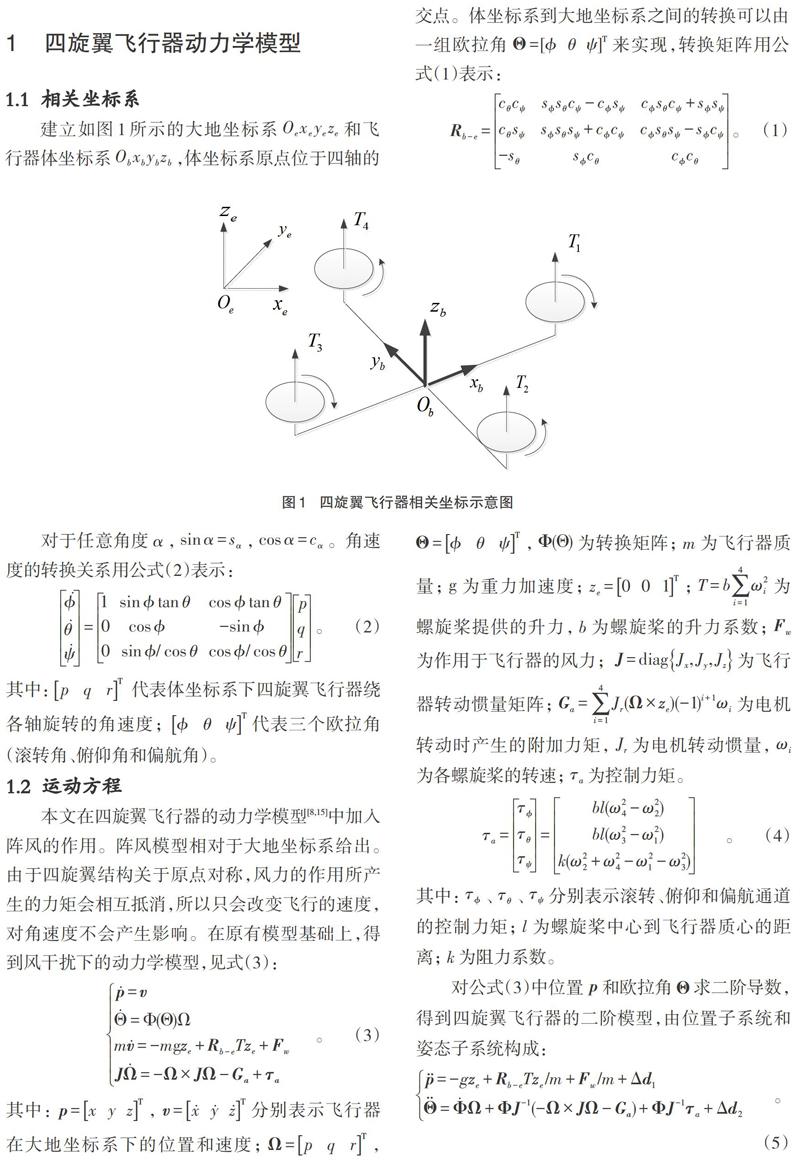
建立如圖1所示的大地坐標系[Oexeyeze]和飛行器體坐標系[Obxbybzb],體坐標系原點位于四軸的交點。體坐標系到大地坐標系之間的轉換可以由一組歐拉角[Θ=[?? ?θ? ?ψ]T]來實現,轉換矩陣用公式(1)表示:
1.2? 運動方程
本文在四旋翼飛行器的動力學模型[8,15]中加入陣風的作用。陣風模型相對于大地坐標系給出。由于四旋翼結構關于原點對稱,風力的作用所產生的力矩會相互抵消,所以只會改變飛行的速度,對角速度不會產生影響。在原有模型基礎上,得到風干擾下的動力學模型,見式(3):
2? ? LADRC控制策略設計
自抗擾控制[16]是由中科院韓京清教授提出的一種不依賴系統精確模型,它是基于誤差消除誤差的新型控制算法,其核心部分擴張狀態觀測器(Extended State Observer,ESO)可將系統內部和外部的總擾動實時地進行估計,從而在控制律設計中作相應的補償。近年來,自抗擾控制也被廣泛應用到飛行器控制領域[17-18]。本文選取調節參數相對較少的線性自抗擾控制[19-20]用于四旋翼飛行器的軌跡跟蹤控制。
為了便于控制器設計,將式(5)改寫為:
設計框圖如圖2所示,由位置回路和姿態回路構成雙閉環控制系統。
2.1? 位置跟蹤控制
設計線性ESO對位置回路總擾動[f1]做實時觀測,ESO的形式如下:
3 仿真分析
控制器參數選擇:
仿真結果表明:無風干擾的情況下,水平面位置大約2 s實現穩定的跟蹤,高度在2 s達到期望的高度值,如圖3(a)所示。圖3(b)所示為姿態跟蹤曲線,滾轉角和俯仰角大約1.7 s實現穩定的跟蹤,偏航角在2 s達到設定值。圖3(c)所示為四個旋翼的升力,各旋翼升力變化平緩,基本維持在2 N左右,總升力[T]為8 N。
10 s之后向系統中加入沿[y]軸正向的常值風,由圖3(a)可以看出[y]軸的位置產生了最大0.33 m的偏移,2 s之后重新達到穩態,[x]軸和[z]軸的位置并未受到明顯的影響。
四個旋翼的升力在加入陣風后有所波動,如圖3(c)所示,隨著自抗擾控制器的調節,2 s之后趨于穩定。為了克服風的干擾,總升力由8 N增加為8.5 N。
同時,由于控制量的變化,引起滾轉角和俯仰角期望值的變化,如圖3(b)所示,2 s之后重新實現穩定跟蹤。
當陣風為正弦風時,[y]軸位置偏離期望軌跡的誤差比常值風增大,且呈正弦形變化。
將本文提出的基于LADRC的控制算法同文獻[8]中基于ESO和反步法的控制方法進行比較。如圖5、圖6所示分別為常值陣風、正弦陣風干擾下,[y]軸位置誤差曲線的對比圖。如表1所示為陣風干擾下,[y]軸產生的最大偏移誤差的對比。
針對四旋翼飛行器位置和姿態的二階系統進行ESO的設計,不依賴于被控對象的精確數學模型,而將子系統的不確定項、外部干擾以及兩個回路之間的耦合看作系統總的擾動進行觀測和補償,最終對象可近似化為二階積分串聯型。所以,在陣風干擾下,LADRC表現出了更優良的性能,且LADRC的設計參數較非線性的ADRC大大減少,更有利于工程的實現。
4? ? 結語
綜上,針對陣風干擾下的四旋翼飛行器軌跡跟蹤控制問題進行研究。在動力學模型中加入風力的作用,控制策略采用位置回路和姿態回路的雙閉環控制,各回路單獨設計LADRC控制器。將子系統的不確定項、外部干擾以及內部耦合看作總的擾動進行觀測和補償。針對常值定向風和正弦風的干擾分別進行仿真,并將結果同現有的算法進行比較,仿真結果驗證了控制策略的有效性和魯棒性。
本文目前只研究了常值定向風和正弦風的干擾,對于其他復雜風場的影響以及執行機構的建模將在以后的研究中加以考慮。
參考文獻:
[1] JIA Z,YU J,MEI Y,et al. Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances[J]. Aerospace Science and Technology,2017,68:299-307.
[2] DYDEK Z,ANNASWAMY A,LAVRETSKY E. Adaptive control of quadrotor UAVs:a design trade study with flight evaluations[J]. IEEE Transactions on Control Systems Technology, 2013,21(4):1400-1406.
[3] ZHOU F, ZHANG Z,LIANG J,et al. Feedback linearization and continuous sliding mode control for a quadrotor UAV[C]// Proceedings of the 27th Chinese Control Conference,2008:349-353.
[4] LEE D,KIM H J,SASTRY S. Feedback linearization vs. adaptive sliding mode for a quadrotor helicopter[J]. International Journal of Control Automation and Systems,2009,7(3):419-428.
[5] ASHFAQ A,WANG D. Modeling and backstepping based nonlinear control strategy for a 6 DOF quadrotor helicopter[J]. Chinese Journal of Aeronautics,2008,21(3):261-268.
[6] 趙元偉,盧京朝.四旋翼飛行器的建模及基于反步法的控制[J].科學技術與工程,2013,13(34):10425-10430.
[7] 滕雄,吳懷宇,陳洋,等.基于反步法的四旋翼飛行器軌跡跟蹤研究[J].計算機仿真,2016,33(5):78-83.
[8] 竇立謙,蘆飛.基于ESO和反步法的四旋翼飛行器軌跡跟蹤控制[J].天津大學學報(自然科學與工程技術版),2017, 50(5):500-506.
[9] RONG X, UMIT O. Sliding mode control of a quadrotor helicopter[C]// Proceedings of the 45th IEEE Conference on Decision & Control, 2006:4957-4962.
[10] 陳增強,王辰璐,李毅,等.基于積分滑模的四旋翼飛行器控制系統設計[J].系統仿真學報,2015,27(9):2181-2186.
[11] ABCI B,ZHENG G,EFIMOV D,et al. Robust altitude and attitude sliding mode controllers for quadrotors[J]. IFAC-PapersOnLine,2017,50(1):2720-2725.
[12] 葉孝璐,俞立,張文安,等.基于串級ADRC的四旋翼飛行器懸停控制[J].中南大學學報(自然科學版),2017,48(8):2079-2087.
[13] 李杰,齊曉慧,韓帥濤.基于自抗擾技術的四旋翼姿態解耦控制方法[J].電光與控制,2013,20(3):44-48.
[14] 楊立本,章衛國,黃得剛.基于ADRC姿態解耦的四旋翼飛行器魯棒軌跡跟蹤[J].北京航空航天大學學報,2015, 41(6):1026-1033.
[15] ZUO Z. Trajectory tracking control design with command filtered compensation for a quadrotor[J]. Control Theory and Application,2010,4(11):2343-2355.
[16] 韓京清.自抗擾控制器及其應用[J].控制與決策,1998,13(1):19-23.
[17] XIA G,LIU Z. Quadrotor unmanned helicopter attitude control based on improved ADRC[C]// 6th IEEE Chinese Guidance,Navigation and Control Conference,2014:916-921.
[18] ZHU E, PANG J, SUN N, et al.? Airship horizontal trajectory tracking control based on active disturbance rejection control (ADRC)[J]. Nonlinear Dynamics,2014,75(4):725-734.
[19] GAO Z. Scaling and Bandwidth-parameterization based controller tuning[C]// Proceedings of the 2003 American Control Conference,2003:4989-4996.
[20] GAO Z. Active disturbance rejection control:a paradigm shift in feedback control system design[C]// Proceedings of the 2006 American Control Conference,2006:2399-2405.
責任編輯? ? 盛? ? 艷

