基于神經網絡的Hammerstein非線性動態系統辨識
劉華卿 李峰 李誠豪 高歌 王翔 楊兵兵 劉宏帥

摘? ? 要:針對單輸入單輸出的Hammerstein非線性動態系統,提出了一種基于神經網絡的Hammerstein非線性動態系統辨識方法。首先,利用BP神經網絡建立Hammerstein非線性系統的靜態非線性模塊,利用自回歸模型建立Hammerstein非線性系統的動態線性模塊;其次,基于二進制信號的輸入和輸出,利用經典的最小二乘方法計算動態線性模塊的未知參數;最后,利用隨機梯度下降方法辨識BP神經網絡的權值。仿真結果表明,提出的方法能夠有效辨識基于神經網絡的Hammerstein非線性動態系統。
關鍵詞:Hammerstein非線性系統;神經網絡;最小二乘;隨機梯度
中圖分類號:TP273? ? ? ? ? ? ? ? 文獻標識碼:A? ? ? ? ? ? ? ?文章編號:2095-7394(2021)02-0009-07
Hammerstein非線性系統由靜態非線性模塊和動態線性模塊串聯而成,是一種典型的非線性系統。研究表明,該系統能夠有效地描述大多數非線性特性,適合蒸餾塔[1-2]、換熱器[3-4]、連續攪拌反應器[5-6]、pH中和過程[7-8]以及干燥過程[9]等過程模型使用;因此,Hammerstein非線性系統得到了系統辨識和自動控制界的廣泛認可和關注。近年來,國內外研究人員提出了諸多Hammerstein非線性系統的辨識方法,主要包括:子空間方法[10-11] 、過參數化方法[12-13]、迭代方法[14-15]、盲辨識方法[16]以及多信號源方法[17-18]等。
在非線性系統的建模研究領域中,神經網絡模型能夠較好地反映對象的動態特性和復雜的非線性映射關系,具有較強的自學習能力和非線性處理能力。近年來,神經網絡模型已成功應用于Hammerstein非線性系統的建模和辨識研究:JANCZAK A [19]利用多層神經網絡逼近Hammerstein模型的靜態非線性,提出了四種不同的在線梯度學習算法來訓練Hammerstein模型;吳德會[20]將Hammerstein模型的辨識問題轉化為神經網絡的訓練問題,再采用誤差反向傳播算法求解迭代訓練問題;WANG W等[21]采用偏最小二乘法對數據進行降維和分數向量提取,內部模型由遞歸神經網絡和Hammerstein模型組成。然而,上述辨識方法雖然取得了較好的辨識效果,但在辨識的模型中包含了模型參數的乘積項,需要通過分解技術將各模塊的未知參數分離出來,因而增加了辨識的復雜度。
針對上述辨識方法中存在的問題,本文提出了一種基于神經網絡的Hammerstein非線性動態系統辨識方法:首先,利用BP神經網絡建立Hammerstein的靜態非線性模塊,利用自回歸模型建立Hammerstein的動態線性模塊;其次,基于二進制信號的輸入和輸出,利用經典的最小二乘方法計算動態線性模塊的未知參數;在此基礎上,基于隨機信號的輸入輸出,利用隨機梯度下降方法辨識BP神經網絡的權值。仿真結果表明,提出的方法能夠有效辨識基于神經網絡的Hammerstein非線性動態系統。
1? ?問題描述
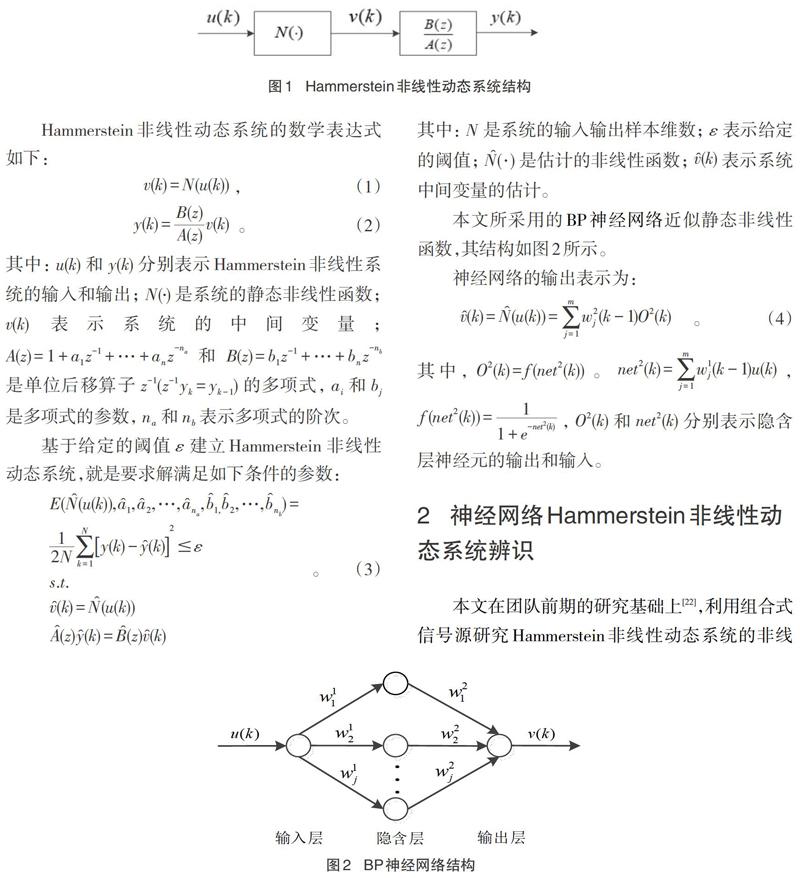
考慮單輸入單輸出Hammerstein非線性動態系統,其結構如圖1所示。
Hammerstein非線性動態系統的數學表達式如下:
2? ?神經網絡Hammerstein非線性動態系統辨識
本文在團隊前期的研究基礎上[22],利用組合式信號源研究Hammerstein非線性動態系統的非線性模塊和線性模塊參數辨識的分離。從圖3可以看出,組合式信號源由幅值為0和非零值的二進制信號以及隨機信號構成。研究表明:如果系統輸入的為二進制信號[u(k)],則相應的中間變量[v(k)]為與[u(k)]同頻率不同幅值的二進制信號,結果如圖4所示;中間不可測變量[v(k)]的值可以利用系統輸入[u(k)]來代替,其幅值的倍數可以用常數增益因子[β]進行補償。因此,在二進制信號作用下,能夠實現Hammerstein非線性動態系統的非線性模塊和線性模塊參數辨識的分離。
2.1? 動態線性模塊的辨識
根據上述分析結果,基于二進制信號的輸入輸出數據,利用最小二乘算法估計動態線性模塊的參數,即:
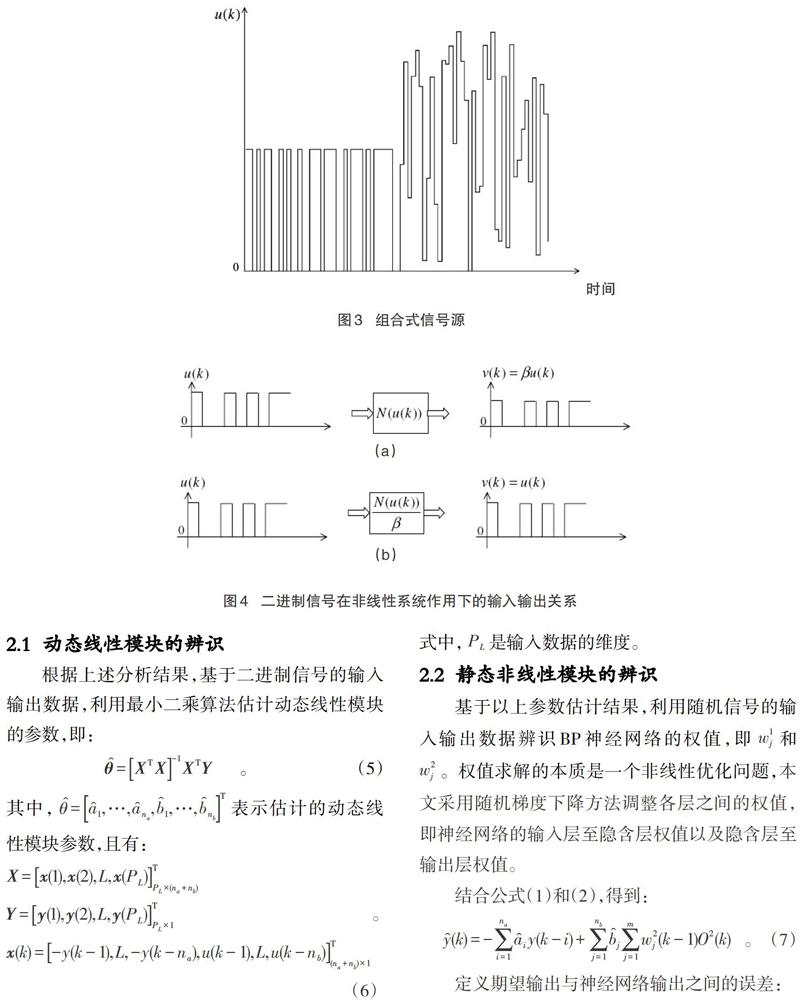
2.2? 靜態非線性模塊的辨識
基于以上參數估計結果,利用隨機信號的輸入輸出數據辨識BP神經網絡的權值,即[w1j]和[w2j]。權值求解的本質是一個非線性優化問題,本文采用隨機梯度下降方法調整各層之間的權值,即神經網絡的輸入層至隱含層權值以及隱含層至輸出層權值。
從式(13)和(17)可以看出,提出的算法只是按照[k]時刻的負梯度方向進行修正,并沒有考慮到[k]時刻之前的梯度方向;因此,導致學習過程發生振蕩,收斂速度慢。為了克服這一問題,在算法中加入動量項。加入動量后的權值更新如下:
3? ? 仿真研究
為了驗證本文提出的兩階段辨識方法的有效性,將該方法運用到Hammerstein非線性動態系統中:
為了辨識神經網絡Hammerstein非線性動態系統的參數,采用如圖5所示的輸入輸出數據。系統輸入數據集包括:(1)200組幅值為0或者1的二進制信號;(2)400組在區間[-1, 1]上均勻分布的隨機信號。
基于二進制信號的輸入輸出數據,利用經典最小二乘算法估計動態線性模塊的未知參數,即:
在動態線性模塊估計的基礎上,基于隨機信號的輸入和輸出數據,利用隨機梯度下降算法辨識靜態非線性模塊的參數,即神經網絡的輸入層至隱含層權值以及隱含層至輸出層權值。文中設置隱含層神經元的數目為12,計算得到:輸入層至隱含層權值為[-3.388 5,-2.446 2,1.601 3,-3.166 5,-0.316 9,-3.172 9,-3.181 4,-2.188 2,-2.484 8,-0.890 1,-3.281 64,-2.963 4];隱含層至輸出層權值為[-0.252 5,0.057 1,1.581 3,-0.314 6,0.772 2,-0.320 3,-0.330 1,0.193 4,-0.073 0,0.355 4,-0.384 7,0.070 9]。
圖6給出了靜態非線性函數的估計,從圖6中可以看出,提出的梯度下降算法能夠有效近似Hammerstein非線性動態系統的非線性模塊。
為了驗證本文提出的兩階段辨識方法的有效性,隨機產生400組測試信號用于辨識系統的預測,系統預測誤差的均方差(Mean Square Error,MSE)為0.043 4,如圖7所示。從圖7中可以看出,提出的方法對Hammerstein非線性動態系統具有較強的預測能力。
4? ? 結語
本文針對單輸入單輸出的Hammerstein非線性動態系統,提出了一種基于神經網絡Hammerstein非線性動態系統的兩階段辨識方法。在研究中,利用BP神經網絡建立Hammerstein的靜態非線性模塊,利用自回歸模型建立Hammerstein的動態線性模塊。在此基礎上,通過組合式信號源實現Hammerstein非線性動態系統靜態非線性模塊和動態線性模塊的分離辨識,其組合式信號源包括二進制信號和隨機信號。首先,基于二進制信號的輸入輸出數據,根據經典的最小二乘方法估計動態線性模塊中多項式模型的參數;其次,利用隨機梯度下降算法估計靜態非線性模塊中神經網絡的輸入層至隱含層權值以及隱含層至輸出層權值。仿真結果表明,提出的兩階段辨識方法能夠有效辨識Hammerstein非線性動態系統中的未知參數。基于本文的研究結果,后續將進一步考慮多輸入多輸出系統,研究多輸入多輸出Hammerstein非線性動態系統的建模和辨識方法。
參考文獻:
[1] RAMESH K, HISYAM A, AZIZ N, et al. Nonlinear model predictive control of a distillation column using wavenet based Hammerstein model[J]. Engineering Letters,2012,20(4):330-335.
[2] BHANDARI B N, ROLLINS D. Continuous-time Hammerstein nonlinear modeling applied to distillation[J]. AICHE Journal,2004,50(2):530-533.
[3] PRSIT D, NEDIT N, FILIPOVIT V, et al. Multilinear model of heat exchanger with Hammerstein structure[J]. Journal of Control Science and Engineering,2016:1-7.
[4] ZHANG H T, LI H X, CHEN G. Dual-mode predictive control algorithm for constrained Hammerstein systems[J]. International Journal of Control,2008,81(10):1609-1625.
[5] LI F, JIA L, PENG D, et al. Neuro-fuzzy based identification method for Hammerstein output error model with colored noise[J]. Neurocomputing,2017,244:90-101.
[6] LI F, Chen L, WO S, et al. Modeling and parameter learning for the Hammerstein-Wiener model with disturbance [J]. Measurement and Control,2020,53(5-6):971-982.
[7] 鄒志云,郭宇晴,王志甄,等.非線性Hammerstein模型預測控制策略及其在ph中和過程中的應用[J].化工學報,2012,60(12):3965-3970.
[8] CHEN H T, HWANG S H, CHANG C T. Iterative identification of continuous-time Hammerstein and Wiener systems using a two-stage estimation algorithm[J]. Industrial and Engineering Chemistry Research,2009,48(3):1495-1510.
[9] LI D, JIA Y, LI Q, et al. Identification and nonlinear model predictive control of MIMO Hammerstein system with constraints[J]. Journal of Central South University,2017,24(2):448-458.
[10] GOMEZ J C, BAEYENS E. Subspace-based identification algorithms for Hammerstein and Wiener models[J]. European Journal of Control,2005,11(2):127-136.
[11] WANG J S, CHEN Y P. A Hammerstein recurrent neurofuzzy network with an online minimal realization learning algorithm[J]. IEEE Transactions on Fuzzy Systems,2008,16(6):1597-1612.
[12] 向微,陳宗海.基于Hammerstein模型描述的非線性系統辨識新方法[J].控制理論與應用,2007,24(1):143-147.
[13] FILIPOVIC V Z. Consistency of the robust recursive Hammerstein model identification algorithm[J]. Journal of the Franklin Institute,2015,352(5):1932-1945.
[14] BAI E W, LI D. Convergence of the iterative Hammerstein system identification algorithm[J]. IEEE Transactions on Automatic Control,2004,49(11):1929-1940.
[15] LIU Y,BAI E W. Iterative identification of Hammerstein systems [J]. Automatica,2007,43(2):346-354.
[16] BAI E W, FU M. A blind approach to Hammerstein model identification[J]. IEEE Transactions on Signal Processing,2002,50(7):1610-1619.
[17] LI F,JIA L,PENG D. Identification method of neuro-fuzzy-based Hammerstein model with coloured noise[J]. IET Control Theory and Applications,2017,11(17):3026-3037.
[18] LI F, JIA L. Correlation analysis-based error compensation recursive least-square identification method for the Hammerstein model[J]. Journal of Statistical Computation and Simulation,2018,88(1):56-74.
[19] JANCZAK A. Neural network approach for identification of Hammerstein system[J]. International Journal of Control,2004,76(17):1749-1766.
[20] WU D.? Neural network identification of Hammerstein nonlinear dynamic systems[C]// Proceedings of the 29th Chinese Control Conference,2010:1242-1246.
[21] WANG W,CHAI T,ZHAO L. Dynamic partial least squares modeling of recurrent neural networks with stable learning[J]. Control Theory and Applications,2012,29(3):337-341.
[22] 李峰,謝良旭,李博,等.基于組合式信號的Hammerstein OE模型辨識[J].江蘇理工學院學報,2019,25(6):66-72.
責任編輯? ? 盛? ? 艷

