基于AFSA的高速無人艇操縱模型參數辨識

楊 鑫，邵 興

（中國船舶重工集團有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

水面無人艇（unmanned surface vessel，USV），簡稱無人艇，是一種無人化的水面智能任務平臺，具有體積小、性價比高、高速智能等優勢，廣泛應用于海洋環境監測、水文地理勘察、海上巡邏與搜救、軍事偵察、反潛作戰等領域，近年來備受各國研究人員關注[1-3]。隨著船用發動機、艇型優化設計、推進技術等的提升，無人艇的設計航速也越來越高，相應的對其操縱性要求也越來越高[4-6]。通常為了對高速無人艇的操縱性進行準確的預報和評估，先要建立比較精確的操縱運動數學模型[7-8]，其中操縱響應模型結構相對簡單，應用方便廣泛，對其研究有重要意義。

無人艇操縱響應數學模型的建立，關鍵是如何確定數學模型中的各個參數。船舶操縱運動模型參數主要通過模型實驗法、CFD仿真計算以及參數辨識法獲得[9]，而參數辨識法較為實用有效。它將操縱運動船舶視為一個動態系統，通過試驗測得系統輸入（舵角、螺旋槳轉速等控制量）和系統輸出（船速、艏向角等運動量），再運用模型辨識方法，對模型中的參數進行求解。

當前，在國內外有部分學者采用一些傳統辨識方法對船舶運動模型進行了求解。趙大明等人應用擴展卡爾曼濾波算法對船舶運動模型參數辨識，在辨識實驗中，采用固定區間卡爾曼平滑算法進行數據預處理，使結果收斂性有一定提升[9]。Sutulo S等人基于經典的遺傳算法，進行了操縱數學模型辨識[10]；上海交通大學的鄒早建團隊，應用支持向量回歸機對船舶操縱運動響應模型進行了機理建模，同時進行改進，結合最小二乘法以及引入粒子群算法對懲罰因子 C值進行尋優，從核函數結構中得到了模型中的操縱性指數[11-13]。

總結分析發現，現有方法在參數辨識過程中，存在計算量大不適合在線辨識或者計算量小但泛化能力較差的問題。人工魚群算法（AFSA）具有高效、智能尋優的特性，所以本文基于AFSA與模型試驗相結合的方法，對高速無人艇的操縱響應模型進行辨識求解，在得到比較精確模型參數的同時也提升了效率。

1 高速無人艇操縱響應數學模型

無人艇操縱響應模型是船舶運動控制領域中應用最廣泛的數學模型。目前對船舶響應模型參數辨識的研究，多數是針對比較簡單的一階線性響應模型，對于需要頻繁操舵以及大舵角操縱運動，非線性模型更精確。常用的一階線性響應模型如下：

式中：r表示艏向角速度；δ為舵角；K為舵效系數，K越大意味著產生的轉艏推力越大，回轉性越好；T表示應舵性和航向穩定性。

考慮到高速無人艇的運動復雜特性，一階線性模型無法有效地描述相應的特性，因而本文對精度較高的一階非線性響應模型中的各項參數進行辨識研究。高速無人艇的一階非線性響應模型可描述如下：

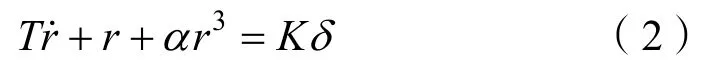
式中：α為非線性項系數，其它變量與式（1）相同。

2 響應模型參數辨識

2.1 人工魚群算法基本原理

人工魚群算法，主要是基于人工魚個體的覓食、聚群和追尾 3種行為進行尋優[14]。在 AFSA中，每條魚的位置被看作是待優化問題的一個可行解，每個解都有一個由適應度函數評估的適應度值。可以針對不同的待優化問題，合理地選擇不同的適應度函數。

在每次迭代中，人工魚會通過覓食、聚群和追尾等行為來更新自己的位置狀態，具體的行為描述如下。

1）覓食行為：地域每一個人工魚，令其當前位置狀態向量為Xi，而向量Xj是人工魚在其視野范圍內任意選擇另一個狀態，如果新狀態的食物濃度Yj大于當前狀態的食物濃度iY，說明得到的狀態優于當前狀態，則向新選擇狀態靠近一步；如果Yj小于iY則重新選取新狀態進行比較，如果選擇次數達到最大次數try_ number后，仍不滿足移動條件，則隨機移動一步。該過程如公式（3）所示：

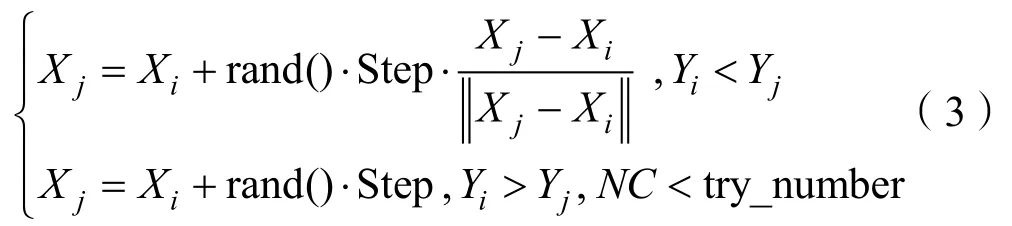
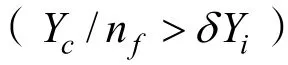
中心位置Xc的數學表達式為

向Xc移動的過程可由公式表示為

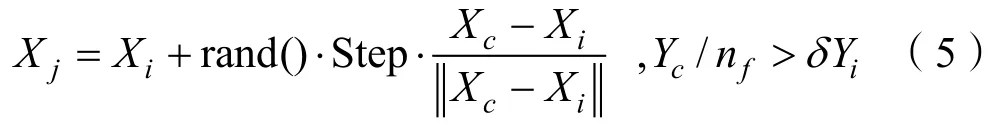
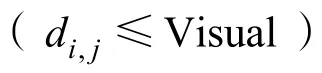
人工魚向Xmax移動過程可由表達式（6）描述如下：

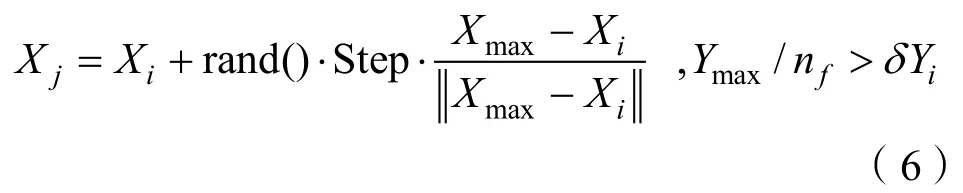
4）公告牌：記錄人工魚最優的狀態。人工魚獲得新的狀態后，與公告牌中記錄的狀態比較，若新獲得的狀態比公告牌中記錄的狀態更優秀，則替換掉公告牌中的狀態；反之，則不變。

人工魚群算法（AFSA）流程如圖1所示。

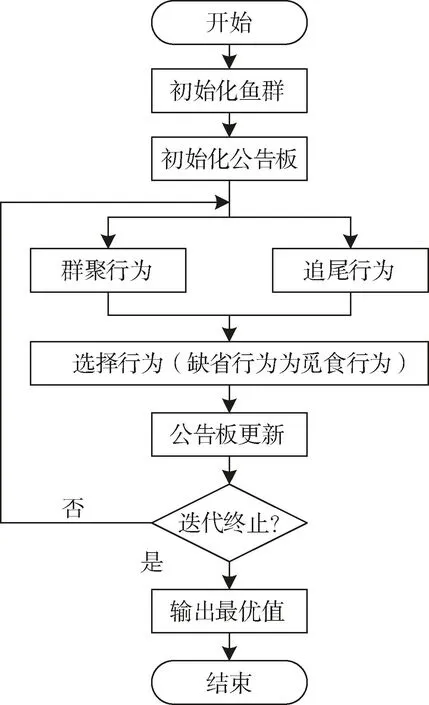
圖1 人工魚群算法流程圖Fig.1 Flow chart of AFSA

上述遞推過程中，首先生成 m條人工魚個體作為初始魚群，在參數區間內為每個人工魚隨機初始化一個位置狀態向量X，然后計算其追尾行為、聚群行為的適應度值Y，采用行為選擇策略，選擇最優的行為作為魚的移動方向，缺省行為是覓食行為。計算出每條魚的食物濃度函數值Y（目標函數），將最優值與公告板中的值進行比較，以完成對公告板上最優的值的實時更新。直到迭代次數達到N，最終公告板中的值就是最優值，對應的狀態向量X即為最優解。

2.2 基于AFSA的構造辨識模型

對于無人艇操縱響應模型，先將模型進行離散化處理，并結合對應的優化方法構建相應的辨識模型，然后進行參數辨識。

通過前向差分法，將無人艇的一階非線性響應模型進行離散化處理，對艏向角速度進行差分可得：

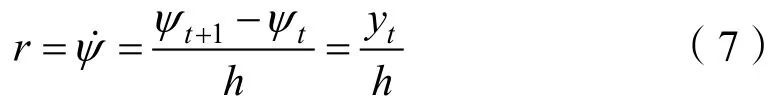
同理，對艏向角速度r的一階導數r˙前向差分，可得：

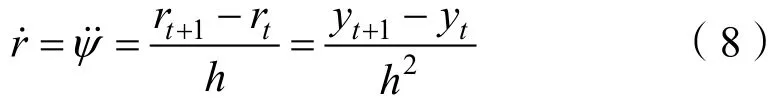
將上述式（7）和式（8）代入一階非線性響應模型式（2），得：

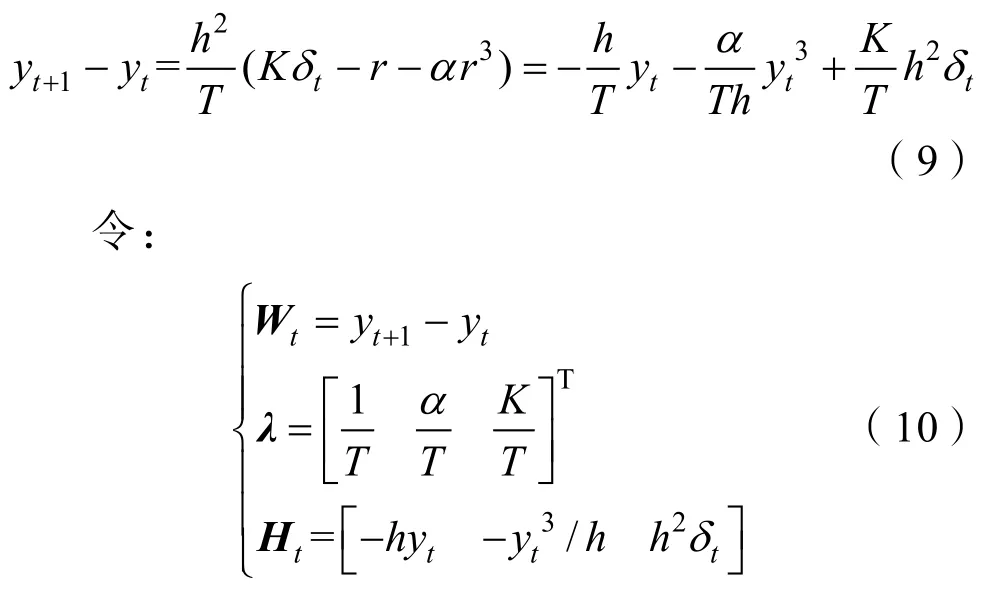
從而可將表達式（10）表示為

由此，將高速無人艇的一階非線性響應模型轉化成離散型系統，從而基于人工魚群算法進行下一步求解。

基于AFSA能夠對狀態向量進行尋優的特性。將式（11）中λ的待辨識元素作為人工魚的位置狀態量X：

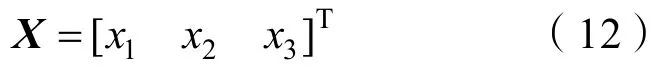
其中：

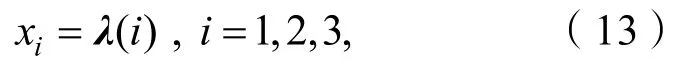
為了辨識得到對應參數值，此處確定適應度函數為

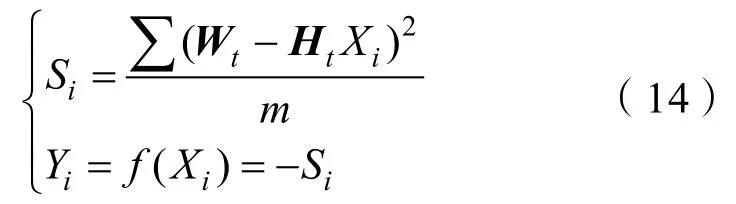
上述適應度函數即為計算樣本的方差，其優化目標即為使得樣本方差S最小。由此將基于人工魚群算法來求解目標函數Y的最大值，即可得到方差S最小情況下的狀態量X。

2.3 采集數據參數辨識

從文獻[15]中選取1組一階非線性響應模型參數，如表1所示。

表1 一階非線性響應模型參數Table 1 Parameters of fist-order nonlinear response model

采用工程上廣泛應用的四階龍格-庫塔法（Runge-Kutta）進行無人艇操縱運動的仿真預報：基于表1中的響應模型開展20°的Z形實驗仿真，得到包括艏向角、舵角、角速度等數據的變化曲線如圖2所示。

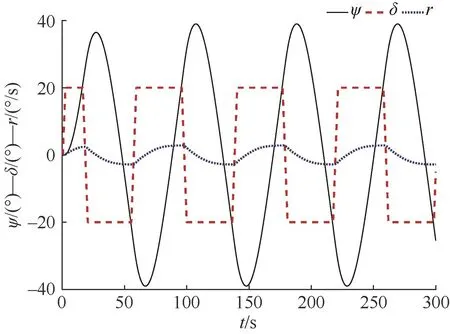
圖2 20°Z形實驗運動仿真結果Fig.2 Results of 20°Z test motion simulation

將圖2中采集的仿真數據帶入式（11）中的Wt和Ht，即可基于AFSA對系統狀態向量X進行狀態估計。其中，人工魚群數量m=100，最大迭代次數N=50，擁擠度因子δ=0.618。

最后，得到適應度函數優化值隨迭代次數變化情況，如圖3所示。

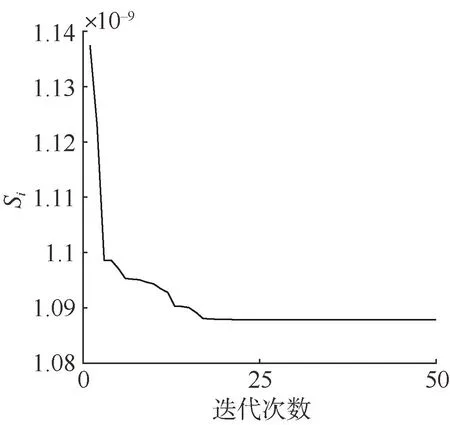
圖3 適應度函數優化結果Fig.3 Optimal result of fitness function

同時，得到狀態向量X中x1～x3的狀態估計值，其辨識結果如圖4-6所示。

圖4 x1的辨識結果Fig.4 Identification result ofx1

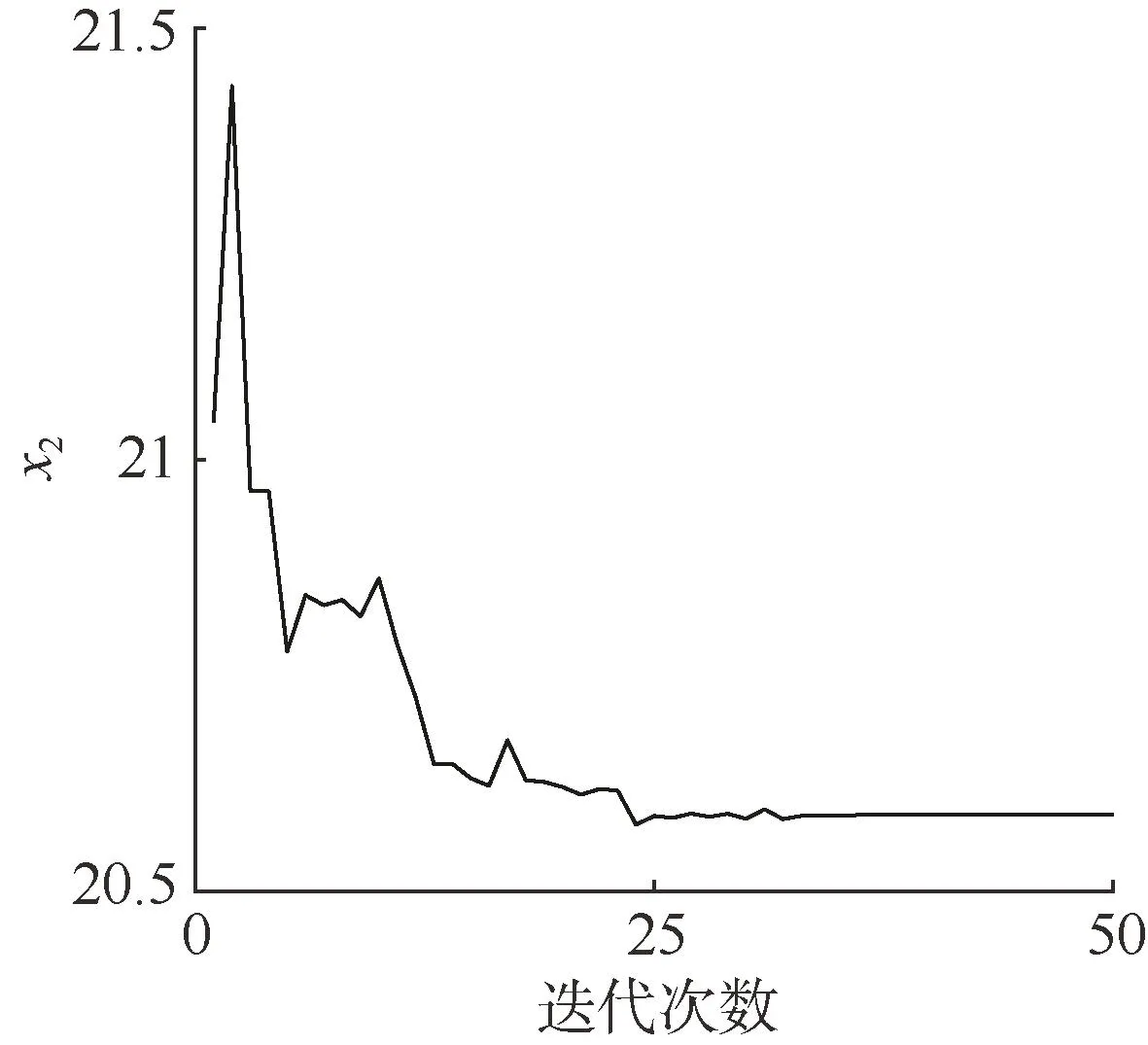
圖5 x2的辨識結果Fig.5 Identification result ofx2

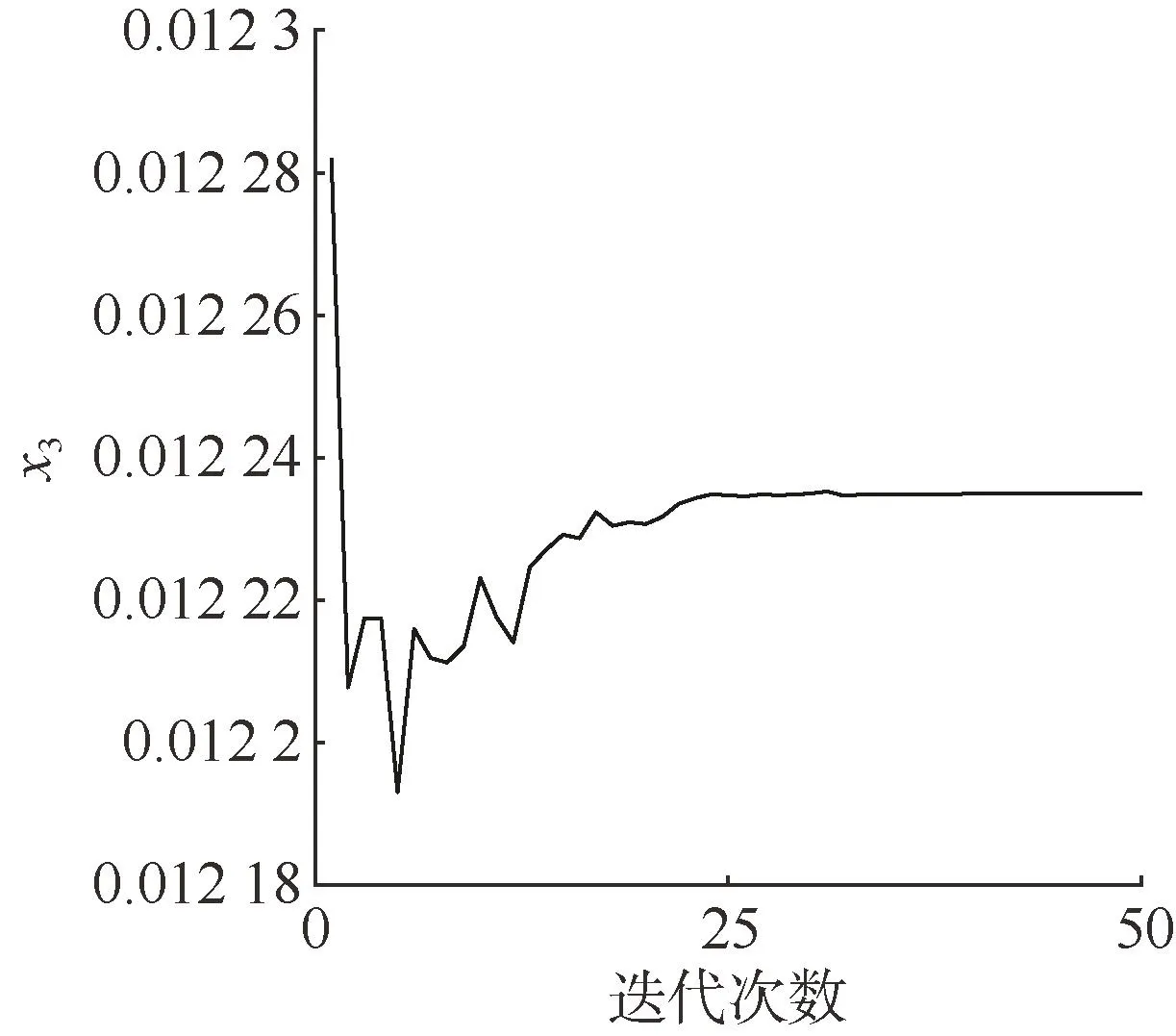
圖6 x3的辨識結果Fig.6 Identification result ofx3

x1～x3的最終辨識結果如表2所示。

表2 x1～x3辨識結果Table 2 Identification result ofx1～x3

由上述表 2可得到式（10）中向量的各個元素辨識結果，進一步解方程即可辨識得到無人艇操縱運動一階非線性響應模型中的各個參數，如表3所示。

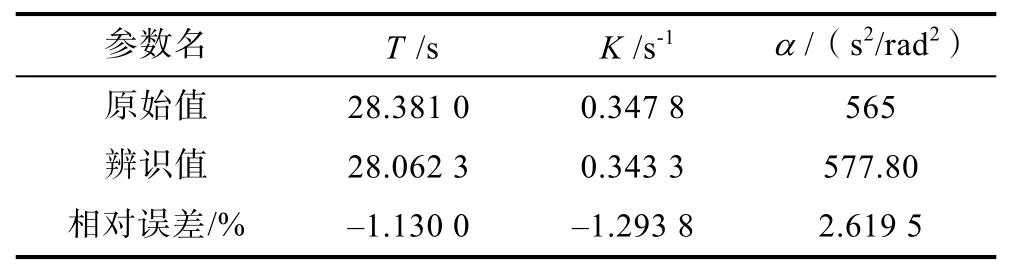
表3 一階非線性響應模型參數Table 3 Parameters of first-order nonlinear response model

由表3可以發現，基于AFSA辨識得到的無人艇操縱運動一階非線性響應模型的各個參數精確度相對較高。

3 辨識結果分析與驗證

為驗證模型參數辨識的最終效果，對辨識所得的響應模型進行操縱運動實驗仿真，并將模型輸出的艏向角變化曲線與原始模型進行對比。首先，分別對原始模型和辨識模型進行20°Z形實驗仿真，其艏向角的變化曲線如圖7所示。

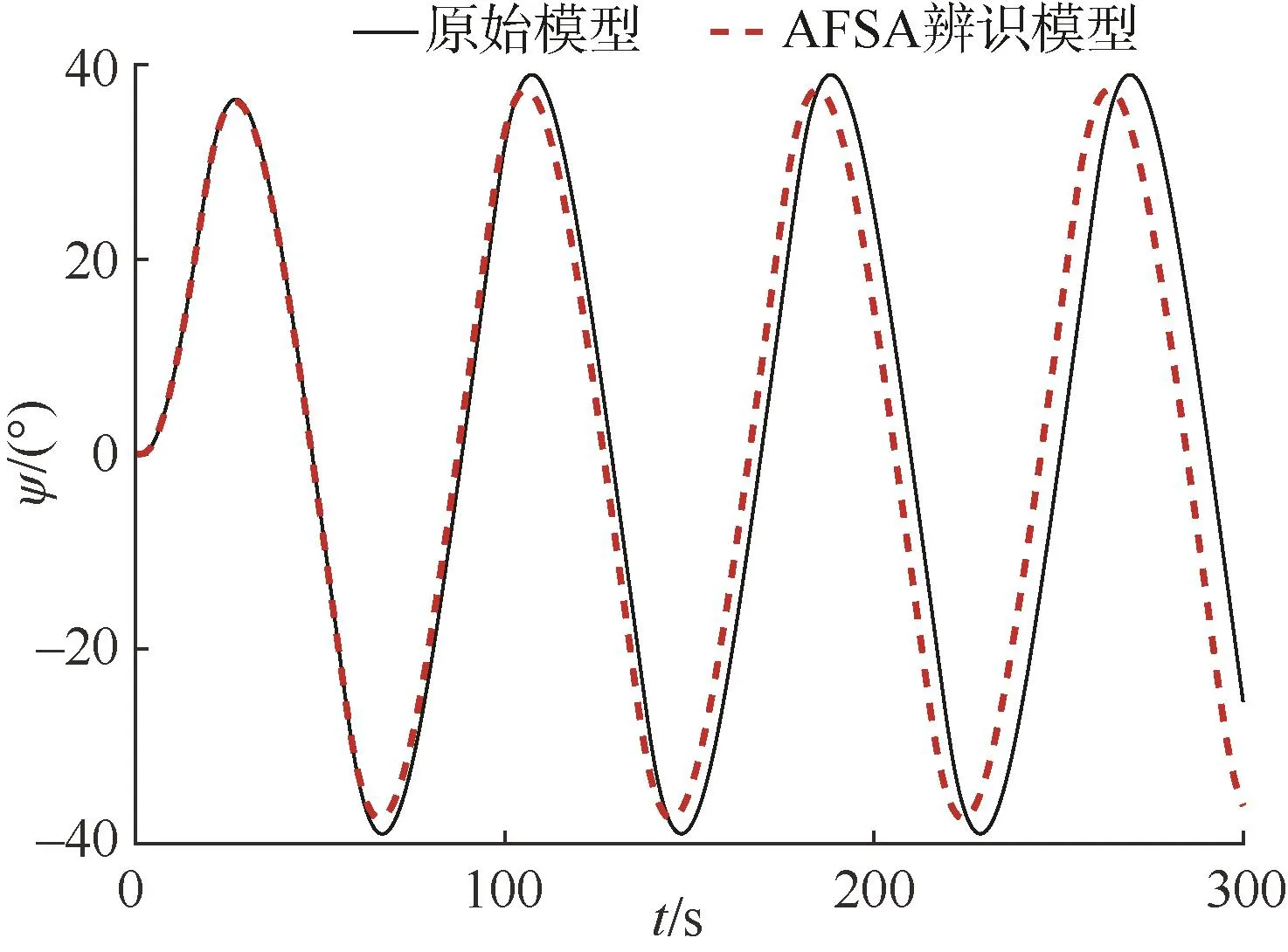
圖7 20°Z形實驗仿真對比Fig.7 Comparison of 20° Z test motion simulation

由圖7可以看出，辨識模型所對應的艏向角變化曲線在前 60 s幾乎與原始模型的艏向角變化曲線重合，誤差很小。隨著時間的推移，兩條曲線的間距逐漸增大。這主要是由于辨識結果與原始模型參數不完全相同，必然會引起誤差。而隨著時間的增加，誤差也不斷累積，最終導致二者的偏差逐漸擴大。

考慮到在無人艇的實際運動控制過程中，舵角會實時根據需要進行改變，從而就不會受到累計誤差的影響，這就說明基于人工魚群算法的響應模型辨識結果能夠較好地為高速無人艇的運動控制服務。

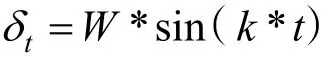
圖 8-9分別為 10°Z形實驗以及 20°正弦操舵仿真對應的艏向角的變化曲線對比圖。

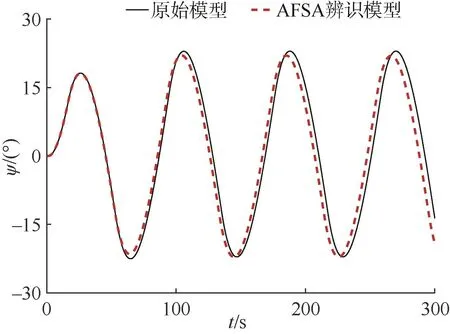
圖8 10°Z形實驗運動仿真Fig.8 10° Z test motion simulation

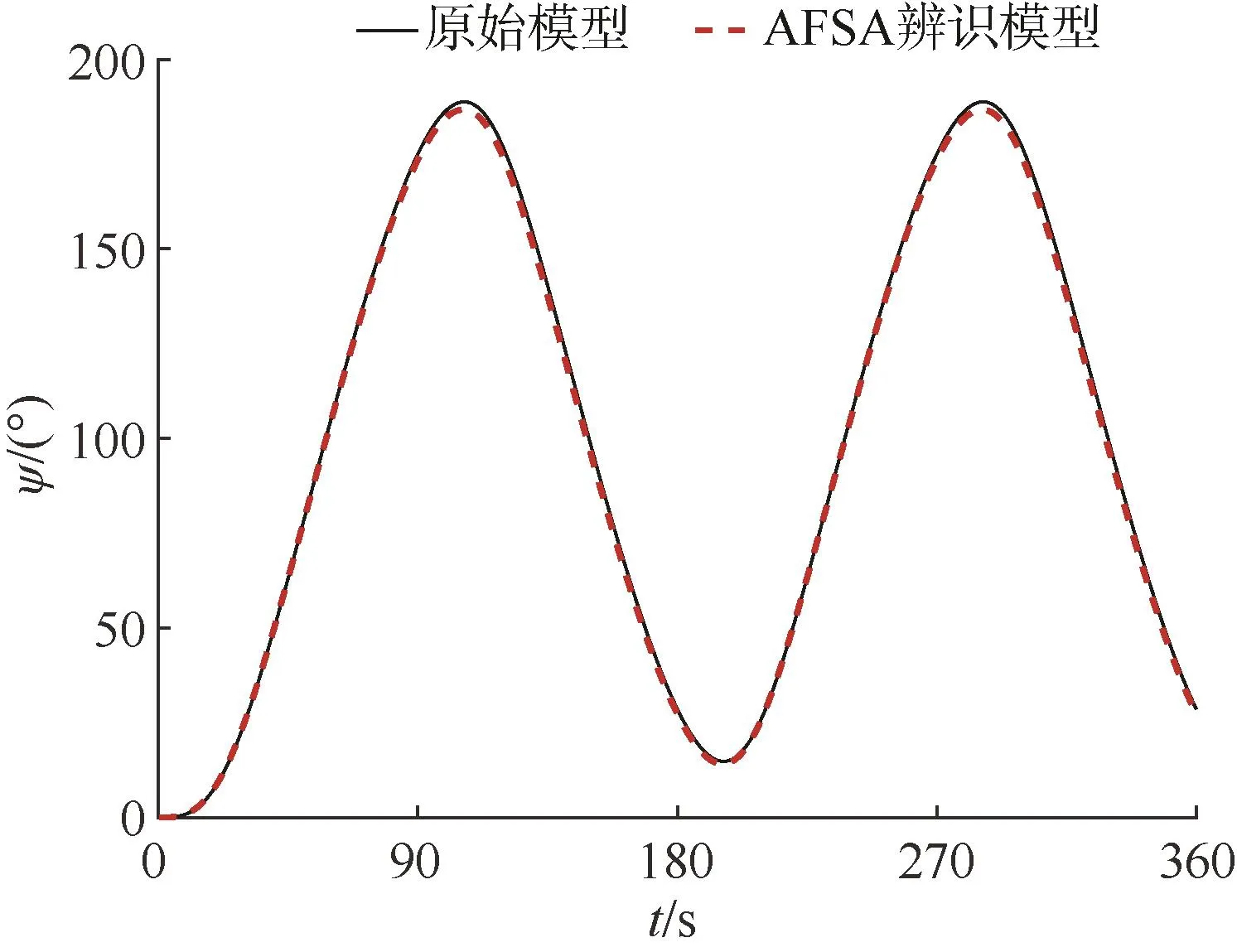
圖9 20°正弦操舵運動仿真Fig.9 Simulation of 20° Sin steering motion

由圖8-9可知，分別從舵角和運動類型兩個維度進行改變，對辨識模型進行不同舵角以及不同類型的運動仿真，其艏向角的變化曲線與原始模型的誤差較小，說明基于人工魚群算法對高速無人艇的一階非線性響應模型參數辨識結果具有良好的泛化能力，能夠較好地適應不同舵角下的操縱運動，從而更好地實現高速無人艇的操縱運動。

4 結束語

針對高速無人艇的運動控制特性，以及其對一階非線性響應模型的需求，本文基于人工魚群算法對高速無人艇操縱運動響應模型的參數進行辨識，并結合相應的操縱運動仿真實驗，得到如下結論：

1）基于AFSA能夠實現對無人艇一階非線性操縱響應模型參數的辨識，并且參數的辨識精確度較高。

2）基于AFSA對高速無人艇操縱模型進行參數辨識過程中，運算量小、辨識結果收斂迅速，保證精度的同時具有高效性。

3）基于人工魚群算法辨識得到的響應模型具有較強的泛化能力，對不同舵角以及不同操舵形式下的操縱運動，都能夠保證足夠的準確性，從而更好地對高速無人艇進行操縱運動控制和預報。