隨機變量和的特征函數的性質與應用

吳雄韜， 史莉娟， 王朝霞

(衡陽師范學院 數學與統計學院， 湖南 衡陽421002)

1 引 言

特征函數是研究隨機變量序列收斂問題的重要工具，大多數概率論與數理統計教材中，給出了獨立情形下特征函數的基本性質[1].作者在2012年研究得到了非獨立情況下二維隨機變量特征函數與原點矩的關系[2]，構造了二階組合數向量和二階混合原點矩向量，建立了二階組合數向量和二階混合原點矩向量與二維隨機變量和的特征函數在t=0處的二階導數的關系.

本文將在文獻[2]研究的基礎上建立隨機變量和的特征函數在t=0處的二階導數與隨機變量協方差矩陣的關系，并結合文獻[3]的研究方法，得到了隨機變量和的特征函數在等相關同分布和獨立同分布情形下兩個推論，證明了等相關同分布隨機變量序列和的特征函數在t=0處的二階導數的極限結果.

2 隨機變量和的特征函數的性質

性質1隨機變量X1，X2，…，Xn，其和的分布的特征函數φ(t)在t=0處二階導數存在.協方差矩陣

A=(akm)n×n=Cov(Xk，Xm)，k，m=1，2，…，n，

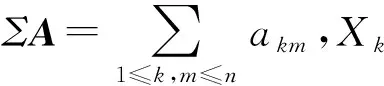
φ″(0)∑A*=0.

證本文僅考慮隨機變量X1，X2，…，Xn為連續型情形，隨機變量其它類型情形可類似處理.

設隨機變量X1，X2，…，Xn聯合密度函數為f(x1，x2，…，xn)，則和的分布的特征函數為φ(t)，

由φ(t)二階可導，則

=-∑A-∑μ*=-∑A*，

由此得

φ″(0)∑A*=0.

推論2隨機變量X1，X2，…，Xn等相關同分布，其和的特征函數φ(t)在t=0處二階可導，

E(Xk)=μ， Var(Xk)=σ2， corr(Xk，Xm)=ρ(k≠m=1，2，…，n)，

其中i為虛數單位，i2=-1，則

證設隨機變量X1，X2，…，Xn協方差矩陣為A，依題意得

設

則

∑A*=nσ2+n2μ2+n(n-1)ρ2，

由性質1知

φ″(0)-n[σ2+nμ2+(n-1)ρ2]，

得

推論3隨機變量X1，X2，…，Xn獨立同分布，其和的特征函數φ(t)在t=0處二階導數存在，

E(Xk)=μ， Var(Xk)=σ2(k=1，2，…，n)，

其中i為虛數單位，即i2=-1，則

3 例子與應用

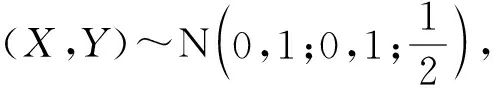
解依題設易知

E(X)=0, Var(X)=1， E(X2)=Var(X)+E2(X)=1，

同理

E(Y)=0， Var(Y)=1， E(Y2)=Var(Y)+E2(Y)=1，

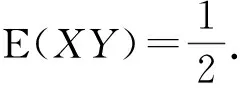
且

從而得φ″(0)∑A*=(-3)+3=0，結論成立.

例2等相關同分布隨機變量序列X1，X2，…，Xk，…，前n項和的特征函數φn(t)在原點二階可導，

E(Xk)=μ, Var(Xk)=σ2， corr(Xk，Xm)=ρ(k≠m=1，2，…，n，…)，

其中i為虛數單位，即i2=-1，則

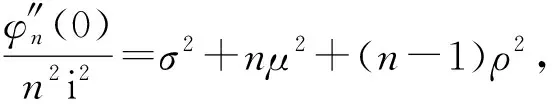
4 結 論

本研究主要運用特征函數定義與性質研究得到了關于隨機變量和的特征函數在t=0處二階導數與協方差矩陣之間關系，給出了性質的兩個推論，證明了等相關同分布序列和的特征函數在t=0處二階導數的極限問題.

致謝作者非常感謝相關文獻對本文的啟發以及審稿專家提出的寶貴意見.