一類廣義B-T方程邊值問題解的存在性
劉筱玥, 江 滟, 邵 悅
(揚州大學 數學科學學院,江蘇 揚州225002)
1 引 言
(1)
的mild解的存在性,其中Dα表示α階Riemann-Liouville分數階導數,Iγ表示γ階黎曼-劉維爾型的分數階積分,f∶[0,1]×→定義為特定函數,它符合相應條件.
階為分數的微積分是由經典整數階微積分推廣而來,在記憶和遺傳材料,流變學和力學系統,高分子材料等物理化學領域都有著廣闊的現實價值.在非整數階的微積分理論不斷開拓創(chuàng)新的大背景下,階為分數的微積分已經成為數學界研究的熱點.文獻[1]在Banach空間中討論了非線性分數階微分方程邊值都為零的情況下解是否存在的問題.
本文旨在討論特定的非線性的分數階的微分方程在其邊值不等于零時解是否存在的問題,設微分方程及其邊值為(1)式.綜合運用Schauder不動點定理等,嘗試討論f在一些比較弱的條件下,邊值問題(1)的適度解是否存在,例如條件為:Caratheodory型條件等.由于當函數的初始值非零時,Riemann-Liouville分數階導數的奇異性帶來困擾,因而初始值非零的情形并非對初始值為零的簡單推廣.
2 預備知識
定義1[2]設h∈L1([a,b];),α>0,定義算子)→C([a,b];)為

定義2[2]設h∶[a,b]→,α>0,n=[α]+1,定義
則上式叫h在t點的α階Riemann-Liouville分數階導數, 式子中的[α]是指實數α的整數部分.
根據Riemann-Liouville分數階積分的定義,能夠推導得到,算子I對指標滿足半群性質,也就是說,對于α,β>0,t∈[a,b],有

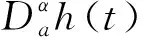

引理1[2]若Dαu∈L1([0,T];),n-1≤α 為討論邊值問題(1)解的定義,先討論相應的線性方程.設g∈C([0,1];),α∈(1,2),β∈(0,1).考慮分數階線性微分方程邊值問題 方程兩邊作用積分算子Iα,得 IαDαu(t)=aIαDβu(t)-Iαg(t). (2) 由于1<α<2,由引理1知,存在常數c1,c2,使得 IαDαu(t)=u(t)+c1tα-1+c2tα-2. (3) 由α階Riemann-Liouville分數階積分的性質得 IαDβu(t)=Iα-βIβDβu(t). (4) 由于0<β<1,由引理1知,存在常數c3,使得 IβDβu(t)=u(t)+c3tβ-1. (5) 將(5)式代入(4)式得 IαDβu(t)=Iα-βu(t)+c3Iα-βtβ-1. (6) 代入(6)式得 (7) 將(3),(7)式代入(2)式,得 化簡后得 上式兩邊應用積分算子I2-α,得 (8) 即 (9) 令 (10) 則(9)式可化為 (11) 在此基礎上,到了邊值問題(1)對應的mild解,并給出定義3. 則稱u是邊值問題(1)的一個mild解,其中P,G1,G2由(10)給出. 記空間C2-α(0,1]={x:(0,1]→|x連續(xù)且存在}.定義范數為 于是此作出以下假設 (T1)f(0,1]×→,符合Caratheodory條件,也就是對于幾乎處處t∈(0,1],f(t,·):→連續(xù);對于u∈,f(·,u):(0,1]→可測. (T2) ?h∈Lp((0,1];+),Ω∶(0,+∞)→(0,+∞)非減局部有界,使得?t∈(0,1],x∈X,有 |f(s,u(s))|≤h(s)Ω(‖u‖), 且 定理1若(T1)、(T2)成立且k1<1,則邊值問題(1)有解. 證定義算子T∶C2-α(0,1]→C2-α(0,1],為 那么容易看出T的不動點就會成為滿足邊值問題(1)的mild解.下面用Schauder不動點定理來輔助證明t2-αTu(t)在題設范圍內存在不動點. 顯然,通過條件(T1), (T2)以及輔助應用控制收斂定理,可以知道T連續(xù). 下一步,要證明有界閉凸集U?B,0∈U的存在,可以使之滿足TU?U,事實是可以證明,由(T2),有 因此可取r>0,使得 從而有 Ω(r)k2‖h‖p+k3+rk1≤r. (12) 記U={u∈C2-α(0,1]∶‖u‖≤r},則顯然U是C2-α的有界閉凸集,對?u∈U,t∈(0,1], 由(T2)及(8)式,利用赫爾德不等式,可得 ≤k3+rk1+Ω(r)‖h‖pk2≤r. 由上面可以推導出t2-αTU?U.而且也容易得到t2-αTU一致有界. 下一步需要證明T映C2-α中有界集為等度連續(xù)集.首先需要假設U?C2-α為有界集,則存在r>0,使得?u∈U,有‖u‖≤r,任取t1,t2∈(0,1],設t2>t1,則 =I1+I2+I3+I4+I5. (13) 由于 (14) 由于α∈(1,2),β∈(0,1),利用積分的絕對連續(xù)性,由(9)-(14)式可得當t2-t1→0時 因此t2-αT映C2-α中有界集為等度連續(xù)集. 至此,證明了t2-αT是連續(xù)的,映有界集為等度連續(xù)集,從而t2-αT為連續(xù)的緊映射,即滿足Schauder不動點定理,因此t2-αT不動點的存在性得以證明, 亦即T不動點的存在性也得以證明,故邊值問題(1)mild解的存在性已證明完畢.定理得證. 進一步地,定理1中的增長性條件(T2)完全可以由下面的次線性增長替換. (T3) 存在a1,a2∈Lp([0,1]∶+),使得|f(t,u(s))|≤a1(t)+a2(t)‖u‖,?t∈(0,1],x∈X. 為方便起見,以下記: 定理2若(T1), (T3)成立,且0 證此定理的證明與定理1的證明非常類似,首先需要定義一個算子T:B→B ≤N3+rN1+N2. 由r的取法可知,N3+rN1+N2≤r,故得‖Tu‖≤r.因此,TU∈U.從以上證明中易見TU一致有界.下面證Tu等度連續(xù).由前證知Tu有界,任取t1,t2∈[0,1],t1 其中 由此易知,t2-αT映C2-α中有界集為等度連續(xù)集. 到這里,已經完成了證明了t2-αT連續(xù)性的證明,以及滿足映有界集為等度連續(xù)集的條件,從而t2-αT為連續(xù)的緊映射,并且使之可以符合應用Schauder不動點定理的條件,從而得知t2-αT在題設區(qū)間內不動點的存在性,也就是說T存在不動點,故存在滿足邊值問題(1)的mild解.至此,定理證明完畢. 本文研究了一類廣義的Bagley-Torvik方程的邊值問題解的存在性.討論是邊值非零的情形.由于Riemann-Liouville分數階導數當初始值非零時具有弱奇異性,因此討論的問題并非齊次邊值問題的簡單推廣.首先討論相應的線性方程,由此得到此類問題的Green函數,給出mild解的定義.在加權的連續(xù)函數空間中,利用Schauder 不動點定理,證明了邊值問題(1)的mild解存在的充分條件. 致謝作者非常感謝相關文獻對本文的啟發(fā)以及審稿專家提出的寶貴意見.3 mild解的存在性
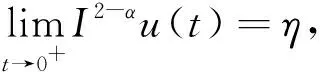
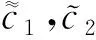
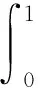
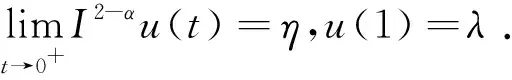
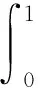

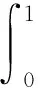


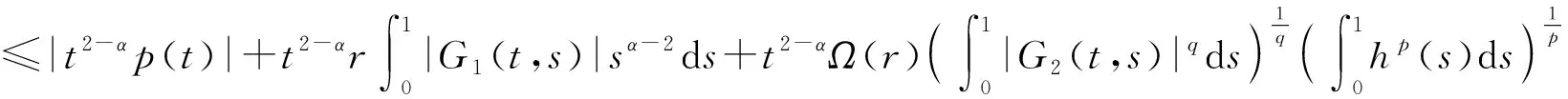
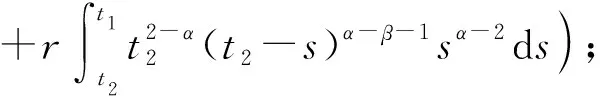
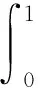


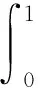
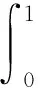
4 結 論

