鋼板彈簧剛度修正系數的取值分析
龍先軍
(東風柳州汽車有限公司商用車技術中心,廣西 柳州 545005)
0 前言
鋼板彈簧作為卡車懸架系統使用最多的彈性元件,連接車架與車橋,傳遞車架與車輪之間的力和力矩,緩和路面對車架及車身的沖擊載荷,衰減由此引起的振動,同時還具有導向及傳遞縱向力、側向力的作用。鋼板彈簧的剛度是懸架設計過程中最重要的性能參數之一,它直接關系到整車的承載能力、平順性能的設計及確定。因此,準確計算鋼板彈簧的剛度對懸架設計具有重要意義。
在鋼板彈簧剛度設計計算時,一般都要引入剛度修正系數ζ,也稱經驗修正系數。引入該系數的主要原因有以下兩點:1)在鋼板彈簧的剛度計算模型中,假設鋼板彈簧的端部受了彎矩,這與實際情況不符;2)在鋼板彈簧的剛度計算模型中,將鋼板彈簧截面簡化成矩形,實際生產中鋼板彈簧的兩側都會軋制成圓角,導致鋼板彈簧斷面慣性矩比理論要小,直接影響鋼板彈簧的剛度。因此,計算鋼板彈簧的剛度時,為了保證計算剛度的準確性,需要引入剛度修正系數ζ對理論計算的剛度進行修正,以保證理論計算剛度與實際剛度相符。
對于剛度修正系數的取值,目前并無統一的標準,文獻[1]建議ζ=0.90~0.95;文獻[2]建議ζ=0.90~0.94;文獻[3]建議ζ=0.90~0.92。同時,多數文獻建議鋼板彈簧片數多,系數取下限;鋼板彈簧片數少,系數取上限;并未對修正系數取值與板簧的類型、厚度、長度等因素做詳細分析。本文通過實際設計工作中鋼板彈簧理論計算剛度值與臺架實測剛度值之間的對比,對剛度修正系數ζ的成因及影響做了分析,并對修正系數ζ取值與鋼板彈簧的類型、規格的關系做了進一步探討分析,總結了更為詳細具體的剛度修正系數。
1 理論分析
1.1 鋼板彈簧的剛度計算
1.1.1 等截面鋼板彈簧的剛度計算
等截面鋼板彈簧(多片簧)長度的一半模型如圖1所示,l1、l2、l3……ln-1、ln分別是第1、2、3……、n-1、n片片長的一半。
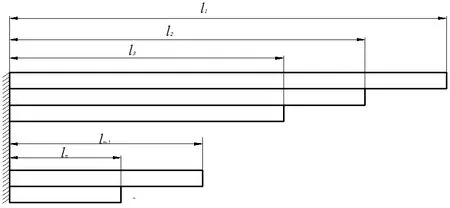
圖1 多片等截面鋼板彈簧的一半
根據汽車設計[2],鋼板彈簧剛度計算方法主要有共同曲率法和集中載荷法。采用共同曲率法計算等截面鋼板彈簧(多片簧)的剛度計算公式如下:
其中:E—材料彈性模量;ξ—修正系數;
ak+1=(l1-lk+1),l1是主片伸直長度半長;lk+1是第(k+1)片的半長,如圖1所示;
Yk—第1片至第K片鋼板彈簧的慣性矩之和的倒數,
Yk+1—第1片至第K+1片鋼板彈簧的慣性矩之和的倒數
Ii—第i片鋼板彈簧慣性矩;b是鋼板彈簧各片寬度,t是鋼板彈簧各片厚度,n是板簧總片數。
1.1.2 變截面鋼板彈簧的剛度計算
變截面鋼板彈簧單片簧的一半模型如圖2所示:
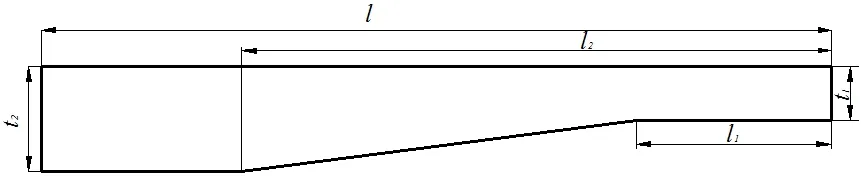
圖2 單片變截面鋼板彈簧的一半
采用共同曲率法計算變截面鋼板彈簧(少片簧)的剛度計算公式如下:
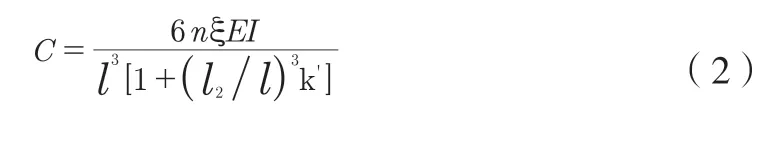
其中:E—材料彈性模量;n—鋼板彈簧片數;
ξ—剛度修正系數;
I—鋼板彈簧慣性矩:
b為鋼板彈簧寬;t1為端部平直段厚度;t2為根部厚度;
l為鋼板彈簧半長;l1為鋼板彈簧端部平直段長度;l2為板變截面段與端部平直段長度之和;如圖2所示。
鋼板彈簧變厚度tx隨長度的變化規律為:
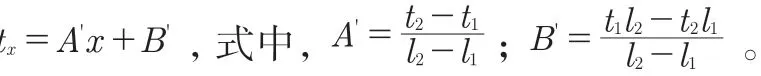
公式中系數k":
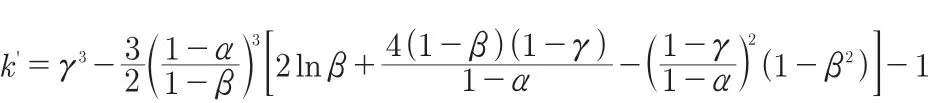
1.2 鋼板彈簧的截面
鋼板彈簧的剛度理論計算中,板簧的慣性矩形截面模型采用如圖3(a)的矩形截面,而實際生產中為了消除材料應力,降低材料重量,將彈簧鋼截面兩側軋制成圓角。根據汽車懸架系統用彈簧鋼第1部分熱軋扁鋼[4],彈簧鋼截面主要有(b)平面半圓角扁鋼、(c)平面矩形扁鋼、(d)單面雙槽扁鋼三種。對于平面半圓角扁鋼(b),側面圓角r≈t/2;對于(c)平面矩形扁鋼,厚度t<40mm時,側面圓角r=8±2mm;厚度t>40mm時,側面圓角r=12±2mm,單面雙槽扁鋼的側面圓角r與半圓角扁鋼相同。
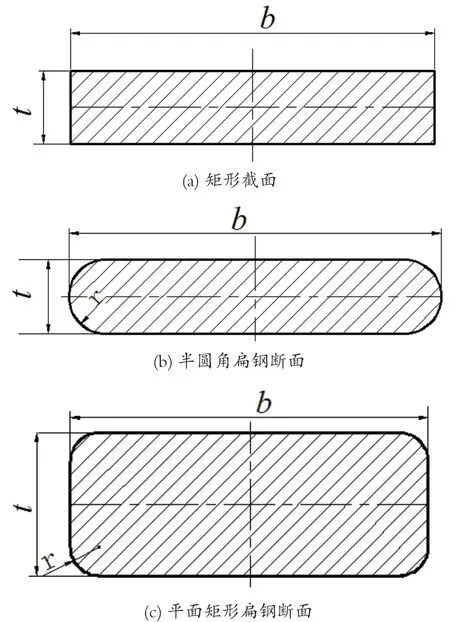
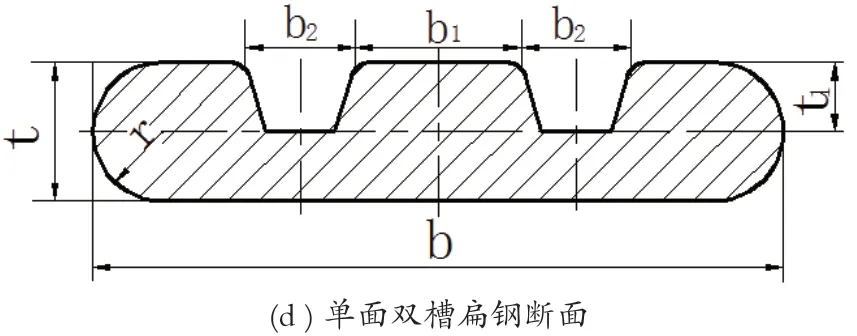
圖3 鋼板彈簧的截面
圖3 (b)、(c)、(d)彈簧鋼截面相對于理論模型的矩形截面(a),斷面面積以及斷面慣性矩均小于矩形截面,下面是矩形截面與半圓角扁鋼的截面積與慣性矩的對比:
矩形截面的鋼板彈簧斷面積:F=bt;
半圓角扁鋼的斷面積:
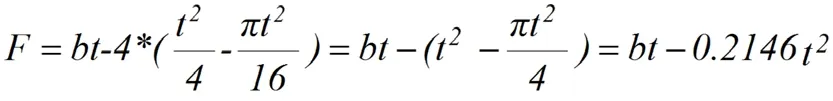
矩形截面的慣性矩:

半圓角扁鋼的慣性矩:

1.3 鋼板彈簧截面對剛度的影響
由鋼板彈簧的剛度計算公式(1)、(2)可知,鋼板彈簧的剛度與截面慣性矩成正比,而截面慣性矩與鋼板彈簧的截面形狀直接相關。我們在鋼板彈簧剛度理論計算模型中,把鋼板彈簧的截當作矩形截面,采用公式(3)計算的慣性矩;實際上鋼板彈簧的兩端都軋制成圓角,截面慣性矩應為公式(4);公式(3)計算的慣性矩要大于公式(4),直接導致計算的理論剛度大于實際剛度。因此,為了保證計算剛度與實際剛度相符,在剛度及應力計算公式(1)、(2)引入剛度修正系數ξ的概念,這是引入鋼板彈簧剛度修正系數的主要原因。
根據鋼板彈簧的剛度計算公式(1)、(2),鋼板彈簧剛度與截面慣性矩成正比,可通過鋼板彈簧截面慣性矩來分析鋼板彈簧截面對鋼板彈簧剛度的影響。
汽車懸架系統鋼板彈簧采用平面半圓角扁鋼,側面圓角r≈t/2,假設兩種鋼板彈簧的寬度分別為70mm、90mm,厚度從10mm至35mm,分別計算矩形截面與半圓角截面的鋼板彈簧慣性矩。
從表1中可知,90mm寬的鋼板彈簧厚度10mm厚時,慣性矩比值系數0.976,鋼板彈簧厚度35mm時,慣性矩比值系數0.916;即相同鋼板彈簧寬度下,厚度越小,系數越大,圓角也就是對鋼板彈簧剛度的影響也就越小;反之鋼板彈簧厚度越厚,對慣性矩(剛度)影響也就越大。鋼板彈簧片厚同是10mm時,90mm寬的鋼板彈簧系數0.976,70mm寬的鋼板彈簧系數0.969;同是片厚35mm,90mm寬的鋼板彈簧系數0.916,70mm寬的鋼板彈簧系數0.893;即鋼板彈簧寬度越寬,系數越大,剛度受到圓角的影響越小。
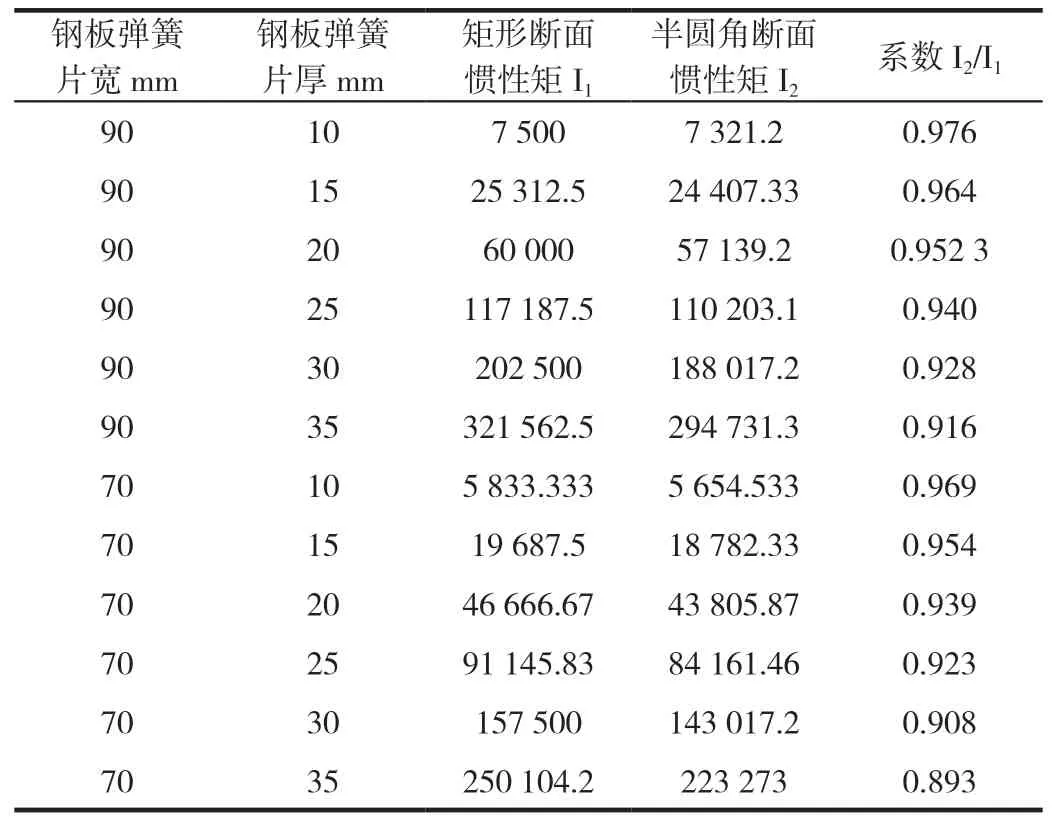
表1 鋼板彈簧寬度、厚度對慣性矩的影響
表1 常用厚度及寬度的鋼板彈簧半圓角斷面與矩形斷面的慣性矩比值在0.89~0.98,各種文獻推薦的剛度修正系數ζ推薦取值0.90~0.95,主要考慮了鋼板彈簧斷面圓角的影響,還有考慮彎矩假設的影響。但是,不同鋼板彈簧的寬度、厚度的剛度修正系數差距也比較大,鋼板彈簧片厚較厚,慣性矩比值較小;鋼板彈簧片厚較薄,慣性矩比值較大。如果ζ取值不合適,如厚鋼板彈簧系數取值0.95,將導致理論計算剛度大于實際剛度;而如薄鋼板彈簧物質0.90,將導致理論計算剛度小于實際剛度。
1.4 鋼板彈簧截面對應力的影響
鋼板彈簧的應力計算公式:

其中:P—鋼板彈簧的端部應力;
L—鋼板彈簧作用長度;
WO—鋼板彈簧斷面系數。
矩形截面的鋼板彈簧斷面系數:

半圓角扁鋼的鋼板彈簧斷面系數:
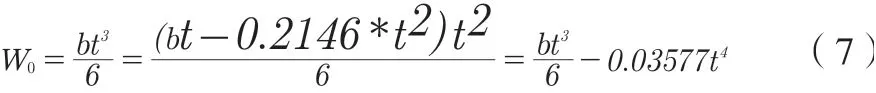
根據公式(5),鋼板彈簧的應力與斷面系數Wo成反比,根據公式(6)、(7)矩形截面的鋼板彈簧斷面系數要大于半圓角扁鋼的鋼板彈簧斷面系數;因此,采用公式(5)鋼板彈簧斷面系數大于實際值,導致計算所得的應力偏小,將影響鋼板彈簧的工作應力設計及判定,影響鋼板彈簧的可靠性。因此,在計算板簧應力時,也需要引入剛度修正系數ξ進行修正。
2 試驗及討論
2.1 試驗
鋼板彈簧的剛度不僅受到鋼板彈簧截面的影響,而且與鋼板彈簧的制造工藝、鋼板彈簧材料等有關。因此,鋼板彈簧的剛度修正系數比考慮圓角的慣性矩比值還要小。通過對鋼板彈簧臺架試驗剛度與理論剛度計算(系數ξ=1)進行比較,總結了各種鋼板彈簧的剛度修正系數。
從表2、表3、表4可知,在理論計算中,如不引入剛度修正系數進行修正,鋼板彈簧實測剛度與設計剛度的誤差將會大于少片簧6%、多片簧8%[5]的設計誤差要求。
表2 對9副等截面鋼板彈簧(多片簧)的試驗實測剛度與理論計算剛度進行對比,剛度修正系數在0.82~0.90,平均值0.86。

表2 等截面鋼板彈簧剛度修正系數
表3 對12副變截面鋼板彈簧(少片簧)的試驗實測剛度與理論計算剛度進行對比,剛度修正系數在0.85~0.94,平均值0.90。
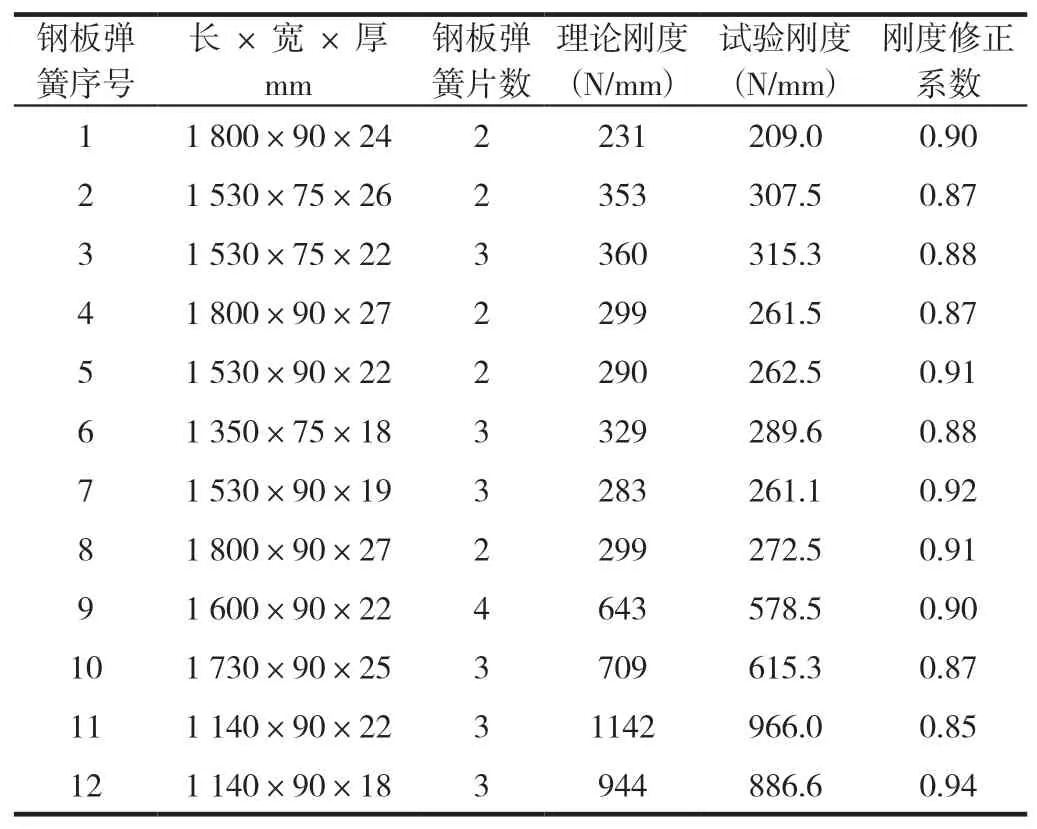
表3 變截面鋼板彈簧剛度修正系數
表4 對5副平衡簧的試驗實測剛度與理論計算剛度進行對比,剛度修正系數在0.77~0.87,平均值0.81。因為平衡簧的作用長度較短,厚度較厚,因此,剛度修正系數都比較小。
表5 中10副等截面鋼板彈簧(多片簧)的理論剛度按公式(4)、(7)計算鋼板彈簧的慣性矩、斷面系數,試驗實測剛度與理論計算剛度比值在0.89~1.01,平均值0.93。
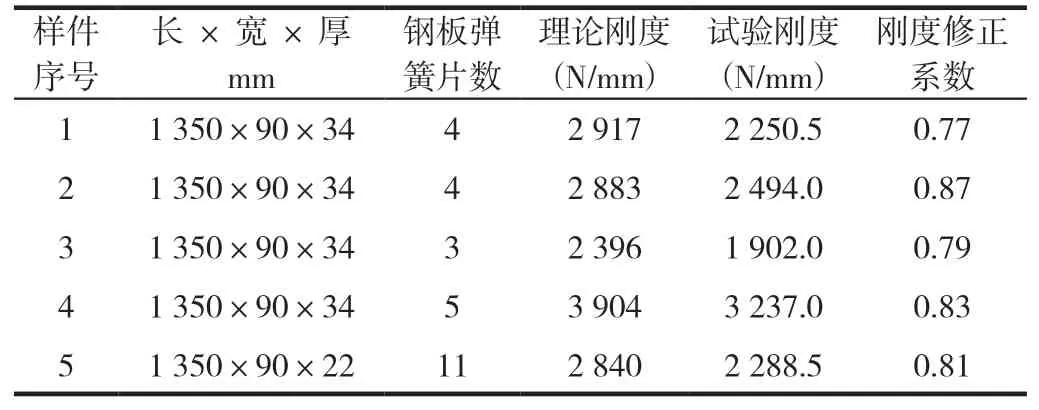
表4 平衡簧剛度修正系數
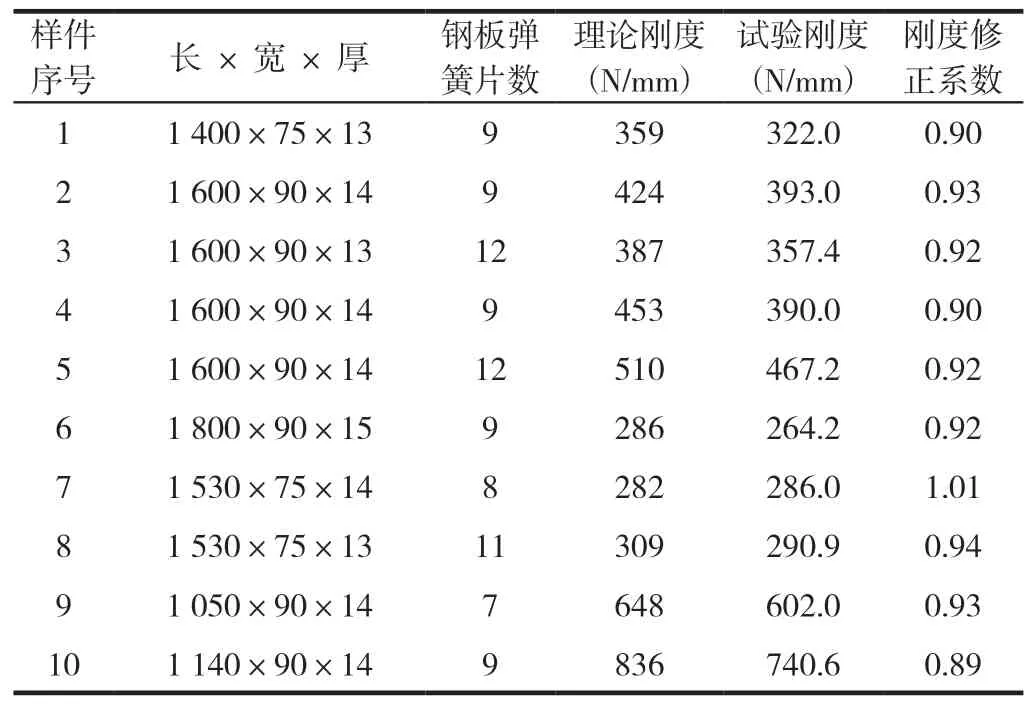
表5 考慮圓角后鋼板彈簧剛度修正系數
2.2 結果討論
根據上述試驗實測剛度與理論計算剛度的之比,等截面鋼板彈簧試驗實測剛度與理論計算剛度的之比的平均值0.86,因此,建議等截面鋼板彈簧的剛度修正系數取值0.84~0.88;對于在剛度及應力計算中,已經在鋼板彈簧慣性矩及斷面系數中消除了鋼板彈簧圓角因素影響的,剛度修正系數可以取0.91~0.95。變截面鋼板彈簧試驗實測剛度與理論計算剛度的之比的平均值0.90,建議剛度修正系數取值0.88~0.92;平衡簧試驗實測剛度與理論計算剛度的之比的平均值0.81,建議剛度修正系數取值0.79~0.83。
3 結語
鋼板彈簧截面影響是引入剛度修正系數的主要原因,影響到板簧剛度及應力的計算。在理論剛度及應力計算中,需要采用剛度修正系數進行修正,以保證理論計算與實測剛度的相符性。剛度修正系數取值直接影響到鋼板彈簧的設計,取值不合適,將導致鋼板彈簧的實測剛度值與理論設計值偏差超出設計規范允許的偏差要求,影響鋼板彈簧承載能力及工作應力,導致設計失敗,需要重新設計校核,影響設計效率及成功率。因此,選擇合適的剛度修正系數對懸架系統的鋼板彈簧設計具有重要意義。
文章通過大量的鋼板彈簧理論計算剛度值與臺架實測剛度值之間的對比,對剛度修正系數ζ的成因、影響、取值做了分析,總結了更為詳細具體的剛度修正系數取值:建議等截面鋼板彈簧的剛度修正系數取值0.84~0.88,如果已經在鋼板彈簧慣性矩及斷面系數中消除了鋼板彈簧圓角因素影響的,剛度系數可以取0.91~0.95。變截面鋼板彈簧剛度修正系數取值0.88~0.92,平衡簧剛度修正系數取值0.79~0.83。鋼板彈簧厚度越厚,系數取值越小;鋼板彈簧越寬,系數取值越大。

