節(jié)水承插式折角彎管水流流動特性研究

弋鵬飛，馬奭文，張建鵬，任 磊，李永發(fā)

（1.伊犁師范大學物理科學與技術(shù)學院，新疆伊寧835000；2.黃河水利委員會信息中心，鄭州450003；3.河海大學水利水電學院，南京210098）

0 引 言

承插式彎管在農(nóng)業(yè)節(jié)水灌溉工程中經(jīng)常使用，不僅含有承插90°的彎管，還有45°、60°等類型的承插折角彎管，它們不僅改變管道水流的方向，還能方便管網(wǎng)的空間布置。這些不同轉(zhuǎn)折角度的承插彎管雖然結(jié)構(gòu)較為簡單，但在轉(zhuǎn)折處流動過程相對復雜。目前學者對90°截面圓形彎管研究較多，曹彪等[1]對不同管徑90°彎頭水流進行了數(shù)值模擬，建立了局部阻力系數(shù)與管徑的關(guān)系式，對比分析了90°彎頭不同流速下的速度場、壓力場特征。L shao 等[2]運用CFD 軟件和試驗對彎管局部阻力損失進行研究，利用壓力傳感器測量彎管前后測壓管水頭，選擇湍流模型對其數(shù)值模擬。Felipe[3]從曲率半徑、管壁粗糙度、流體溫度因素對彎管進行了試驗，發(fā)現(xiàn)彎曲段的二次流現(xiàn)象導致了能量耗散。江山[4]、孫業(yè)志[5]分別對90°彎管內(nèi)部的水流和空氣流動，采用湍流數(shù)學模型對流場進行數(shù)值模擬，分析管內(nèi)壓力分布、二次流動、壁面壓力系數(shù)的變化。賀益英等[6]對彎管局部阻力的影響因素、規(guī)律進行了討論，推薦了常用的一些彎管局部阻力系數(shù)經(jīng)驗公式。綜上所述，研究者[7-9]主要對90°彎管內(nèi)流體流態(tài)和局部水頭損失相聯(lián)系，分析兩者之間的關(guān)系。

本文以供水管網(wǎng)中45°、60°及90°的承插折角彎管作為研究對象，對其水流流動和局部阻力系數(shù)研究計算，分析彎管內(nèi)部流動特征及所產(chǎn)生的能量損失機理，計算水流對彎管的沖擊力，為供水管網(wǎng)恒定流水力計算和管網(wǎng)非恒定流建模提供參數(shù)[10]。

1 承插式45°彎管流阻特性試驗及理論分析

試驗系統(tǒng)見圖1，主要實物見圖2。選取折角45°的DN50型有機玻璃彎管進行試驗。利用位于泵房水池中的潛水泵向高位水箱不斷供水保持恒定水頭。通過彎管前端的蝶閥和水箱水位控制進入彎管流量，測壓管布置在彎管中心上下游10倍管徑處，測量彎管前后水頭差，量取三角堰水位，計算管道流量值。調(diào)節(jié)水箱的水位2.0～5.2 m，管道流速可調(diào)至0.5～3.0 m∕s ，每個試驗流速操作重復3 次，彎管兩端壓力測點，測量3次取平均值。

根據(jù)伯努利方程計算彎管的局部阻力系數(shù)，對彎折處前后10倍管徑處取斷面1-1和2-2，寫出能量守恒關(guān)系式：

式中：z1為1-1 斷面位置水頭；p1為1-1 斷面壓強；z2為2-2斷面位置水頭；p2為2-2 斷面壓強；u1、u2為管道流速；hw為1-1斷面到2-2斷面之間的總水頭損失。

在數(shù)值模擬時，假設(shè)認為彎管的進出口位置水頭與速度水頭是相等的。取進口壓力與出口壓力差作為總的水頭損失，總水頭損失是沿程水頭損失與局部水頭損失的總和。根據(jù)《水力學》[11]中的布拉休斯公式可以得到沿程阻力系數(shù)λ，并計算沿程阻力損失，總水頭損失減去沿程水頭損失獲得局部水頭損失，再推求出局部阻力系數(shù)。

式中：ν為流體運動黏滯系數(shù)；d為管道直徑；Re為雷諾數(shù)。

2 承插式折角彎管的流場數(shù)值模擬計算

2.1 數(shù)學模型選取

試驗流態(tài)根據(jù)雷諾數(shù)判斷，屬于湍流狀態(tài)。數(shù)值計算模型采用Relizablek-ε湍流模型，該模型在模擬射流和混合流的自由流動、旋轉(zhuǎn)均勻剪切流、管道內(nèi)部流動、邊壁分離流動及二次流可以與真實湍流情形吻合較好[12,13]。模型包括不可壓縮流體的連續(xù)方程、動量方程，湍動能和耗散率輸運方程，聯(lián)立解出流場質(zhì)點三維速度值和壓強值。模型如下：

連續(xù)方程：

動量方程：

湍動能方程：

耗散率方程：

μt、Cμ按照下式計算：

式中：Gk為平均速度梯度產(chǎn)生的湍動能；Gb為浮力影響產(chǎn)生的湍動能；YM為可壓縮流脈動膨脹對總的耗散率的影響；σk、σε分別為湍動能和湍動能耗散率對應的湍流普朗特數(shù)。

2.2 承插式彎管幾何建模與參數(shù)設(shè)置

折角彎管模型在Gambit 中建立，為消除上下游邊界對計算區(qū)域流態(tài)的影響，使湍流充分發(fā)展，幾何模型上下游模擬的尺寸取管徑的10 倍長度。網(wǎng)格劃分采用六面體和四面體相結(jié)合，六面體網(wǎng)格元素為Hex∕Wedge，類型為Cooper，四面體網(wǎng)格元素為Tet∕Hybrid，類型為TGrid。由于水流局部水頭損失主要發(fā)生在這一段，所以在彎曲段上、下游2D 范圍加密。選用基于壓力的分離式求解器，采用SIMPLEC 算法求解流場，壓力項差分選用標準格式，動量、湍動能、耗散率均采用二階迎風格式。流態(tài)設(shè)為定常流。

邊界層設(shè)置方法見文獻[13]。進出口邊界條件設(shè)置分別是速度入口和自由出流，湍流強度估算為5%，湍流黏度取值為0.04，出口邊界設(shè)置為自由出流，收斂精度取值0.001。

DN20、DN40、DN50、DN63、DN75折管生成的網(wǎng)格數(shù)在186 534～323 146 之間。模擬前進行網(wǎng)格無關(guān)性驗證，即劃分的網(wǎng)格數(shù)對其模擬值大小不再影響。圖3為45°承插彎管局部網(wǎng)格及邊界層劃分示意圖。

3 結(jié)果與分析

3.1 承插式折角彎管試驗結(jié)果與模擬分析

通過數(shù)值模擬相同試驗條件下0.5～3.0 m∕s 進口速度下水流的流場，計算得出DN50 型45°彎管局部阻力系數(shù)值，并與試驗值相比較。

經(jīng)過對比發(fā)現(xiàn)試驗值與模擬值變化規(guī)律相似，在雷諾數(shù)7.9×104（u=1 m∕s）之前，起始有一個變化較快的降低趨勢，隨著雷諾數(shù)的增大，局部阻力系數(shù)逐漸減小，且變化微小并趨于穩(wěn)定，穩(wěn)定后的試驗平均值為0.264，數(shù)值模擬平均值為0.226，試驗值和模擬值較為接近，說明采用的Relizablek-ε模型是精確可信的。所以后續(xù)對45°、60°、90°彎管內(nèi)部流場特征研究采用數(shù)值模擬方法（見圖4）。

圖5～圖7為DN50 型承插式45°彎管在入口流速為2 m∕s 的管道剖面壓力云圖、速度云圖、局部流線及二次流軌跡圖。

從壓力云圖可以看出彎管的轉(zhuǎn)折段對管道壓力變化影響較大，在下游管道出現(xiàn)較大的壓強梯度，轉(zhuǎn)折后上壁面由于流體質(zhì)點分離產(chǎn)生負壓，90°彎管的負壓程度較為嚴重，相同的幾何位置處，比45°、60°的彎管負壓值大，可達-6 000 Pa。由于離心力的作用，大部分水流沖擊外側(cè)管壁，在彎曲段外壁出現(xiàn)壓強最大值。

從速度云圖可以看出流速在彎曲段發(fā)生了劇烈的變化，水流拐彎后受慣性力的作用，流體質(zhì)點聚集在外邊壁，內(nèi)邊壁由于質(zhì)點回流出現(xiàn)水流收縮形態(tài)，流速梯度在收縮段急劇增大，速度最大值出現(xiàn)45°折管下游，最大值可達3.4m∕s。從DN50 型的45°、90°承插彎管局部流線圖上可以看出，在拐彎處有渦旋和回流現(xiàn)象發(fā)生，拐彎50 mm 處的縱斷面上顯示了二次流運動軌跡[14]，管壁兩側(cè)有清晰的漩渦，且是呈對稱形狀，旋向相反，渦核處流線密集分布?；亓鲄^(qū)的形態(tài)大小和管道內(nèi)水流速度和轉(zhuǎn)折角度有關(guān)。根據(jù)文獻[15]中描述：其他條件一定時，當流經(jīng)管道內(nèi)壁的轉(zhuǎn)折邊為銳邊時，管流阻力變大，水流發(fā)生劇烈地脫離內(nèi)邊壁的現(xiàn)象。與承插45°彎管相比，90°承插彎管的回流區(qū)明顯擴大至100 mm處。回流區(qū)的流體質(zhì)點夾雜在管道主流中發(fā)生摻混，經(jīng)過下游管段一段距離后，流動逐漸調(diào)整均勻，在彎曲段流動方向改變和回流、渦旋現(xiàn)象是引起承插式折角彎管局部水頭損失的主要原因。

圖8分別為承插DN20、DN40、DN50、DN63、DN75 規(guī)格45°、60°、90°折角彎管的局部阻力系數(shù)與雷諾數(shù)變化的關(guān)系曲線。

在0.5～6.0 m∕s 入口流速下，不同規(guī)格的45°、60°、90°承插彎管局部阻力系數(shù)隨雷諾數(shù)變化規(guī)律基本相同，在低雷諾數(shù)區(qū)到較高雷諾數(shù)時局部阻力系數(shù)發(fā)生降低，隨著雷諾數(shù)增大，水流進入阻力平方區(qū)后，局部阻力系數(shù)趨于穩(wěn)定，可以認為此時的局部阻力系數(shù)與雷諾數(shù)無關(guān)，這與電磁閥[16,17]、球閥[18,19]等不同結(jié)構(gòu)的灌溉連接元件局部阻力系數(shù)變化規(guī)律相似。不同管徑的承插彎管進入阻力平方區(qū)的雷諾數(shù)大小不一致，DN20 彎管流動的雷諾數(shù)在2.9×104就進入了阻力平方區(qū)，DN75彎管流動的雷諾數(shù)在1.0×105后進入阻力平方區(qū)，可見管徑越小的承插彎管，進入阻力平方區(qū)所需的雷諾數(shù)越小。

表1為不同管徑承插角度的彎管水流進入阻力平方區(qū)后，局部阻力系數(shù)趨于穩(wěn)定的大小分布。從表1看出管徑大小對局部阻力系數(shù)影響較弱，折角大小對局部阻力系數(shù)影響規(guī)律明顯，隨著折角沿著水平線彎折角度增加，局部阻力系數(shù)也逐漸增大。根據(jù)進入阻力平方區(qū)的局部阻力系數(shù)統(tǒng)計，45°、60°、90°承插彎管的局部阻力系數(shù)分別為0.213、0.462、1.127。

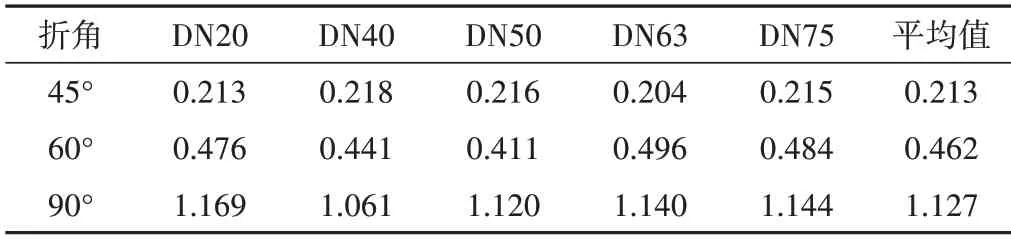
表1 不同管徑承插彎管局部阻力系數(shù)表Tab.1 The different diameter of bend pipe local resistance coefficient

3.2 水流對彎管的沖擊力

水流對彎管的彎曲段沖擊力較大，沖擊力直接作用在管壁上，對管道有沖擊破壞作用，實際工程中將采取混凝土鎮(zhèn)墩等有效措施來對流速較高的鐵質(zhì)或混凝土管道的彎曲段防護，而節(jié)水灌溉中的管道多為PVC 材料，承壓強度相對較低，所以對上述折角彎管在不同流速下的沖擊力進行計算，和管道承壓值進行比較，為PVC灌溉管道安全運行提供理論指導。

在計算水流對彎管的沖擊力時，可以用動量方程來求解。下面以45°折角彎管流速2 m∕s為例計算水流對彎管的沖擊力。

計算步驟：①取彎曲段過水斷面1-1 和2-2 之間的水體為控制體，選取水平面xoy為坐標平面，如圖9所示。過水斷面取距離轉(zhuǎn)折中心2倍的管徑處，該位置處為水流形態(tài)發(fā)生的變化劇烈處，對彎曲段沖擊力最強烈。②分析控制體所受的全部外力，在控制體上標出各力的作用方向?？刂企w內(nèi)部水流的重力G 沿垂直方向，故在xoy平面上投影為0。兩端面過水斷面的1-1 和2-2 的動水壓強可以通過Fluent 軟件讀取。已知p1=-206.681 76 Pa，p2=-1 201.427 1 Pa。截面壓強采用絕對壓強計量。

控制體內(nèi)的水流流動遵循能量守恒方程：

由于是等徑管v1=v2=2 m∕s；動能修正系數(shù)α1=α2= 1.0。

管壁對控制體的作用力R，是水流對彎管沖擊力的反作用力，以相互垂直的分量Rx和Ry表示。假定其方向如圖10所示。

X方向的動量方程為：

同理，Y方向的動量方程為：

水流對彎管的沖擊力Nx和Ny方向與Rx和Ry方向相反，大小相等。合力大小是兩個分力的合成。

對DN50 規(guī)格彎管的沖擊力與流速采用最小二乘法方法擬合關(guān)系式為：

從上述擬合關(guān)系式可以得出水流對彎管沖擊力與流速的平方成正比關(guān)系，相同速度下，折角越大，沖擊力也越強。從計算結(jié)果得出水流速度10 m∕s 時，對彎管的壓強值為204 780.56 Pa，超過PVC 灌溉管最低抗壓值0.2 MPa，將對管道安全運行造成隱患。

4 結(jié) 論

本文用試驗和數(shù)值模擬方法研究了折角彎管中水流流態(tài)變化，以及流態(tài)引起的局部水頭損失變化，并計算了穩(wěn)態(tài)流動的不同管徑局部阻力系數(shù)及水流對彎曲段的沖擊力。得出以下結(jié)論：

（1）承插折角彎管局部阻力損失主要發(fā)生下游轉(zhuǎn)折處，轉(zhuǎn)折處水流有回流產(chǎn)生，橫截面處有一對等大對稱旋向相反的渦旋二次流形成，回流和二次流現(xiàn)象是引起局部水頭損失的主要原因。

（2）承插折角彎管局部阻力系數(shù)隨著雷諾數(shù)的增大而逐漸降低，水流進入阻力平方區(qū)后，局部阻力系數(shù)趨于恒定，彎折角度越大，局部阻力系數(shù)也越大，45°、60°、90°承插彎管的局部阻力系數(shù)分別為0.213、0.462、1.127，可為供水管網(wǎng)水力計算提供取值依據(jù)。

（3）計算了水流對彎管的沖擊力，擬合了流速與沖擊力的數(shù)學表達式，該計算公式可確定折角彎管的安全流速范圍，為供水管網(wǎng)安全運行提供理論依據(jù)。