多級行星輪系結構與運動拓撲模型的圖形符號描述方法及其運動學分析

王均剛， 楊士男， 劉燕德， 曾禮平， 墨蕊娜

(1.華東交通大學 機電與車輛工程學院，江西 南昌 330013； 2.華東交通大學 理學院， 江西 南昌 330013)

行星齒輪傳動因其特殊的結構和優良的傳動性而被廣泛應用于各種機械傳動系統。與單級行星輪系相比，多級行星輪系的結構復雜，包含的構件更多，對多級行星輪系的分析設計十分困難[1-2]。

國內外學者日益重視應用圖形符號對行星輪系進行結構拓撲分析，提出了豐富的圖論表示方法[3-6]。薛隆泉等[7]基于功能離散法提出行星輪系的拓撲圖轉化理論，通過拓撲變換過程、借用不同的符號表示出行星輪系中各構件以及構件間不同的聯接特征，最終形成以點、線組成的圖形，但其在整體結構拓撲性表達方面存在欠缺。雷亞榮[8]在文獻[7]基礎上，完善了拓撲圖的轉化理論，確立行星輪系系統化研究的圖形模型，見圖1，但是其對構件的符號表示以及構件間的聯接性質仍未作到明確的區分，整體結構情況不完整，缺少機架與其他構件的聯接關系，各構件間的聯接特征不明確，齒輪內嚙合和外嚙合無法進行區分。

圖1 兩級行星輪系結構圖及結構拓撲模型[8]

文獻[9-12]基于圖論理論，對行星齒輪傳動機構進行構型方案設計。Ding等[13]提出了新雙色拓撲圖和三色拓撲圖的方法，并在平面連桿機構的構型綜合中取得了很好的效果。李斌等[14]引入新三色拓撲圖對行星齒輪機構進行結構描述，見圖2，運用新三色拓撲圖對行星輪系進行拓撲描述時，雖然能夠明確地體現出各構件間的聯接特征以及構件的性質，但輪系的整體結構特性反映不太明確。

為了使運算復雜、難以掌握的行星輪系運動學分析變得更為簡單和直觀， 一些研究者采用圖形化方法對行星輪系的運動學進了分析。Tsai等[15]運用方塊圖法對行星輪系的運動特性進行了分析。GomAyats等[16]針對行星輪系中各構件之間的運動關系以及整個傳動系統的傳動比分配，提出了一種超圖法。Salgado等[17]基于圖形表示法對具有多構件的行星輪系功率流與傳動效率進行了分析。Gao等[18]在行星輪系中引入速度拓撲圖的概念，研究了傳動比和拓撲之間的關系。符升平等[19]基于圖論理論，提出了一種更適用于計算機建模和求解的行星輪系傳動性能分析方法。

由文獻可知，采用圖形符號能夠簡化行星輪系的結構設計和運動學分析。但是，用于研究行星輪系結構特征以及運動特性的各類圖形化表示呈現發散式研究，各有千秋。盡管有學者研究了統一拓撲描述模型的平面機構的表示方法[20]，但目前公開發表的文獻尚無針對多級行星輪系的結構特征及運動特征信息運用完善的圖形符號進行表示，并且對多級的行星輪系進行結構和運動拓撲描述時相對困難，甚至無法作出其拓撲圖。

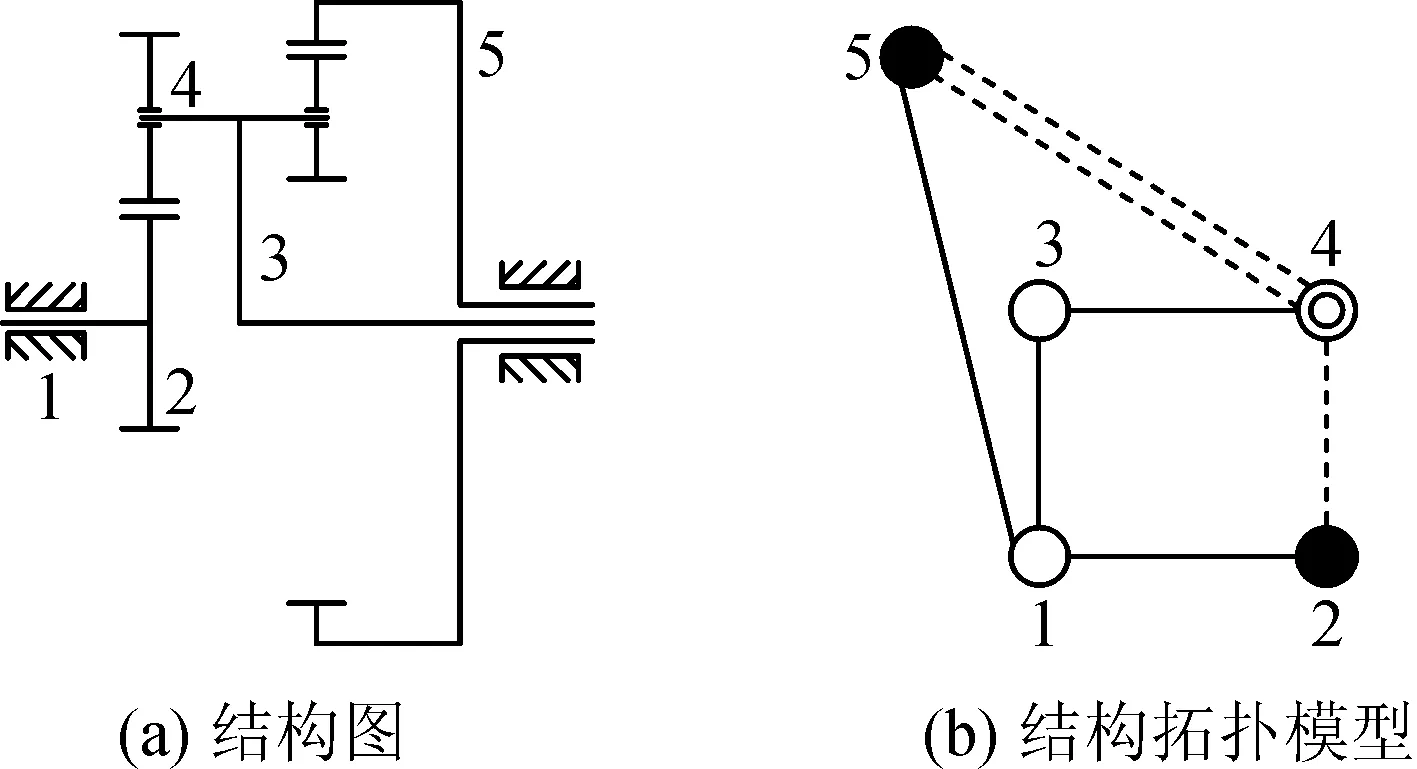
圖2 單級行星輪系結構圖及結構拓撲模型[14]

本文在已有的研究基礎上，提出了對多級行星輪系的結構特征及運動特征信息運用完善的圖形符號進行表示方法，該方法能夠對多級的行星輪系進行結構和運動拓撲模型進行描述。通過對行星輪系中各構件以及各構件之間的聯接關系進行相關的圖形符號定義，規定了演化規則及轉換方式，提出了能夠完整描述行星輪系整體結構特征、運動特性和構件性質明確的統一圖形符號表達方法，為行星輪系在實際分析設計過程中提供一種新的方式。其具體分析過程見圖3。

圖3 行星輪系拓撲模型建立分析流程圖

1 描述行星輪系統新圖形符號及其轉換規則

應用圖論理論對行星輪系進行研究，需要滿足以下兩種情況：1)拓撲模型反映的行星輪系的整體結構情況是否完整；2)拓撲模型反映的行星輪系的運動性質情況是否明確。同時，這兩種情況是根據以下三方面的指標進行分析：①圖形的運動拓撲反映是否明確，運動拓撲性具體指輪系各構件間的聯接特征；②圖形中構件性質是否明確，構件性質具體指輪系中構件的區分度和所屬功能；③圖形的整體結構拓撲特性反映是否明確，整體結構拓撲特性具體指不同性質的構件所屬的層不同。

一般而言，行星輪系是由太陽輪、行星輪、內齒圈、行星架以及機架所組成的傳動系統。基于拓撲圖轉化理論，將行星輪系中各構件轉化為不同的圖形符號進行描述。

1) 各功能構件符號描述：實心點●表示單行星輪、復合實心點?表示雙聯行星輪；空心點○表示太陽輪；空心方框□表示行星架；實心方框■表示內齒圈；空心三角形△表示機架。

2) 各功能構件的聯接關系轉化規則：細實線表示回轉副；單嚙合線表示齒輪外嚙合聯接；雙嚙合線表示齒輪內嚙合聯接，忽略機架與基本構件之間的固結。

3) 根據行星輪系的基本回路特性，在圖畫的表示中，圖形符號表示的基本回路為應滿足基本回路數目等于系統的齒輪副數目，且由表示三個基本構件的圖形符號、表示齒輪副圖形符號、兩個回轉副圖形符號構成的封閉回路。

2 基于新圖形符號的多級行星輪系統結構與運動拓撲模型

2.1 多級行星輪系統結構拓撲模型

根據上述中各構件的圖形符號定義，現建立圖4中兩級行星輪系的結構拓撲模型。

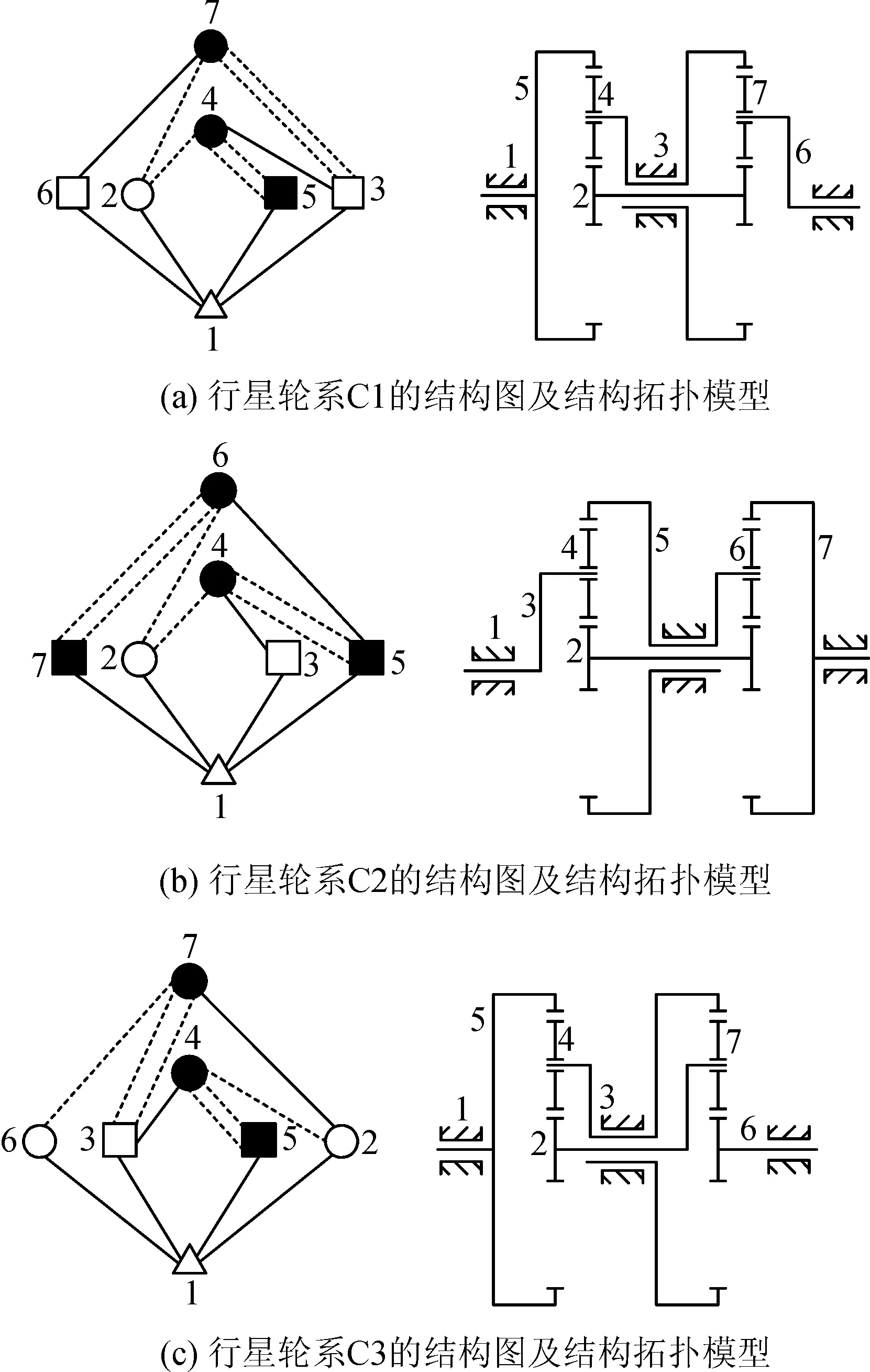
圖4 兩級行星輪系結構圖及結構拓撲模型

將行星輪系的結構圖轉化為結構拓撲模型表示，其主要優點之一是便于建立行星輪系的鄰接矩陣[12]，對行星齒輪機構進行同構性判斷。行星輪系的鄰接矩陣形式以及轉換規則為：

(1)

式中：n為機構的構件數，矩陣元素aij(i、j=0,1,2,…,n)。若構件i、j以回轉副聯接，則aij=1；若構件i、j以外嚙合齒輪副聯接，則aij=2；若構件i、j以內嚙合齒輪副聯接，則aij=3；若構件i、j以外嚙合齒輪副聯接且含有雙聯行星輪時，則aij=4；若構件i、j以內嚙合齒輪副聯接且含有雙聯行星輪時，則aij=5；其余，aij=0。

根據式(1)，建立圖4中兩級行星輪系C1、C2和C3的鄰接矩陣A，即：

(2)

(3)

(4)

通過編程，分別計算出鄰接矩陣A的特征值及特征向量，具體計算結果見表1～3(其中，第一列為特征值λ，其右方為與該特征值相對應的特征向量φ，φ=[φi]T，i=1,...,7)。通過對比鄰接矩陣的特征值和特征向量進行行星齒輪機構之間的同構判斷[21]。

通過對比行星輪系C1、C2和C3的鄰接矩陣的特征值與特征向量，可知C1與C2的鄰接矩陣的特征值完全相同，并且同一特征值所對應的特征向量其各元素對應相等或比例，例如λ3=-0.699 7所對應的特征向量：φ1?(-φ1)、φ2?(-φ2)、φ3?(-φ5)、φ4?(-φ4)、φ5?(-φ7)、φ6?(-φ3)、φ7?(-φ6)，因此，可以判斷行星輪系C1與C2為同構運動鏈；行星輪系C3與C1或C2，首先其鄰接矩陣的特征值就不相等，不滿足判斷條件，因此，行星輪系C3與C1或C2之間的為非同構運動鏈。

表1 鄰接矩陣AC1的特征值和特征向量

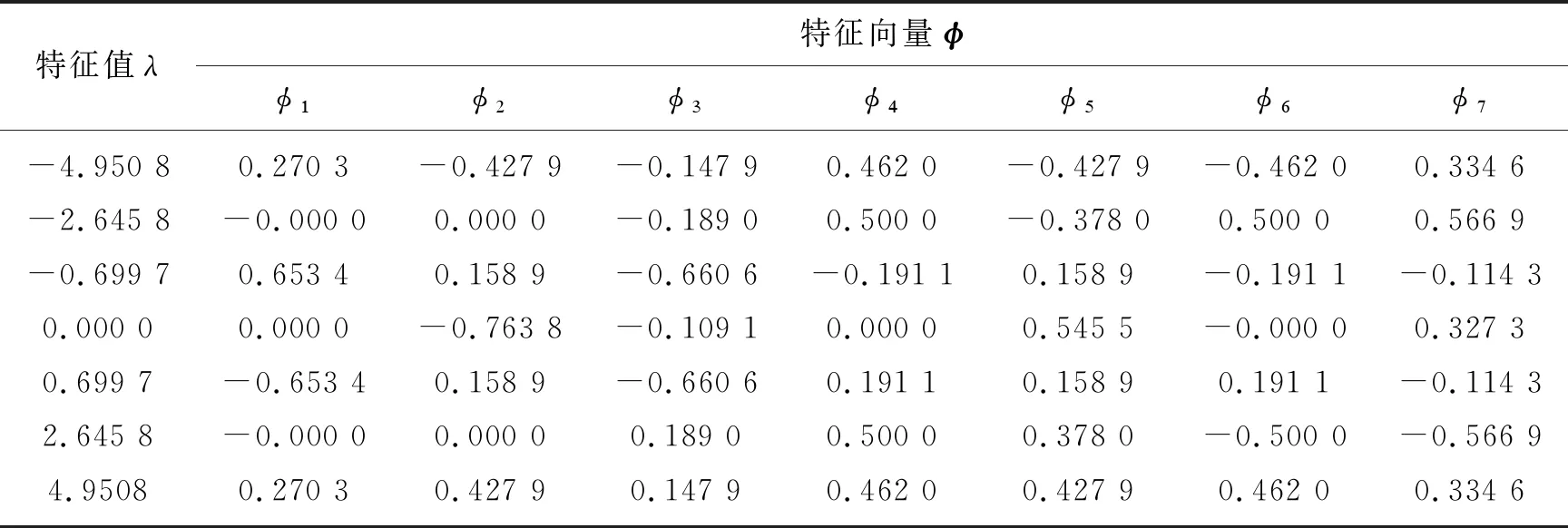
表2 鄰接矩陣AC2的特征值和特征向量

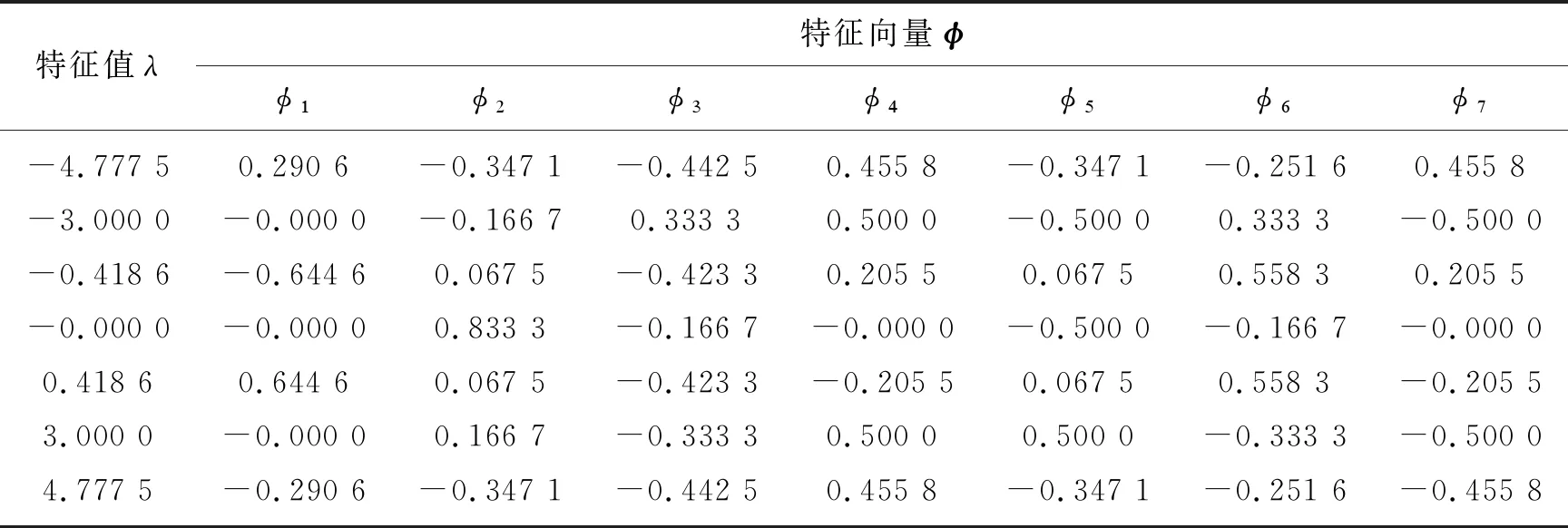
表3 鄰接矩陣AC3的特征值和特征向量

2.2 多級行星輪系的運動拓撲描述模型

行星輪系的運動拓撲模型是反映其運動狀態的特征模型。無論是單級行星齒輪傳動或多級行星齒輪傳動都可以分解為外嚙合和內嚙合兩種基本運動功能單元，見圖5，其中p表示行星輪、s表示太陽輪、r表示內齒圈、c表示行星架。

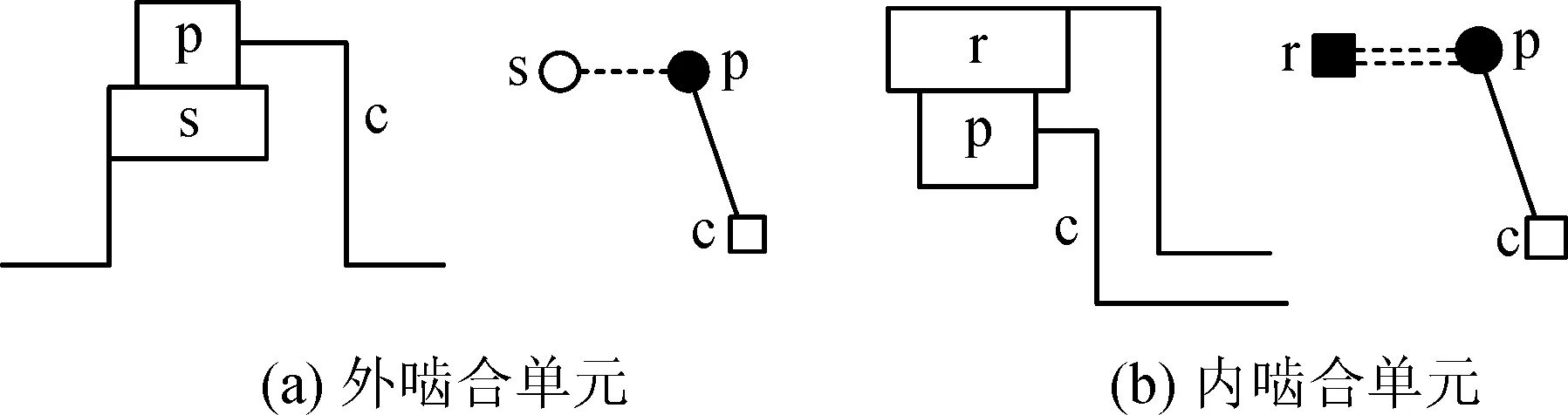
圖5 行星齒輪基本運動單元

以每個基本運動單元轉化為定軸輪系后的傳動比為特征，根據行星齒輪機構中基本運動單元內各構件的運動關系建立其轉速方程：

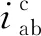
3 運動分析實例

為了驗證多級行星輪系結構與運動拓撲模型的圖形符號描述新方法的有效性和簡單直觀性，以圖6(a)所示的復式行星齒輪機構為例進行運動學實例分析。復式行星傳動系統由復式太陽輪2、復式行星架3、復式行星輪4、復式內齒圈5、復式雙聯行星輪6和6′和太陽輪7組成，其動力傳遞分為兩路：一路為復式行星架3帶動復式行星輪4、復式雙聯行星輪中的行星輪6與分別與復式內齒圈5和復式太陽輪2嚙合傳動；另一路為復式行星架3帶動復式雙聯行星輪中的行星輪6′與太陽輪7嚙合傳動。通過建立其運動拓撲模型，并進行基本運動單元劃分，分別對各構件的轉速ω以及系統的總傳動比進行求解。

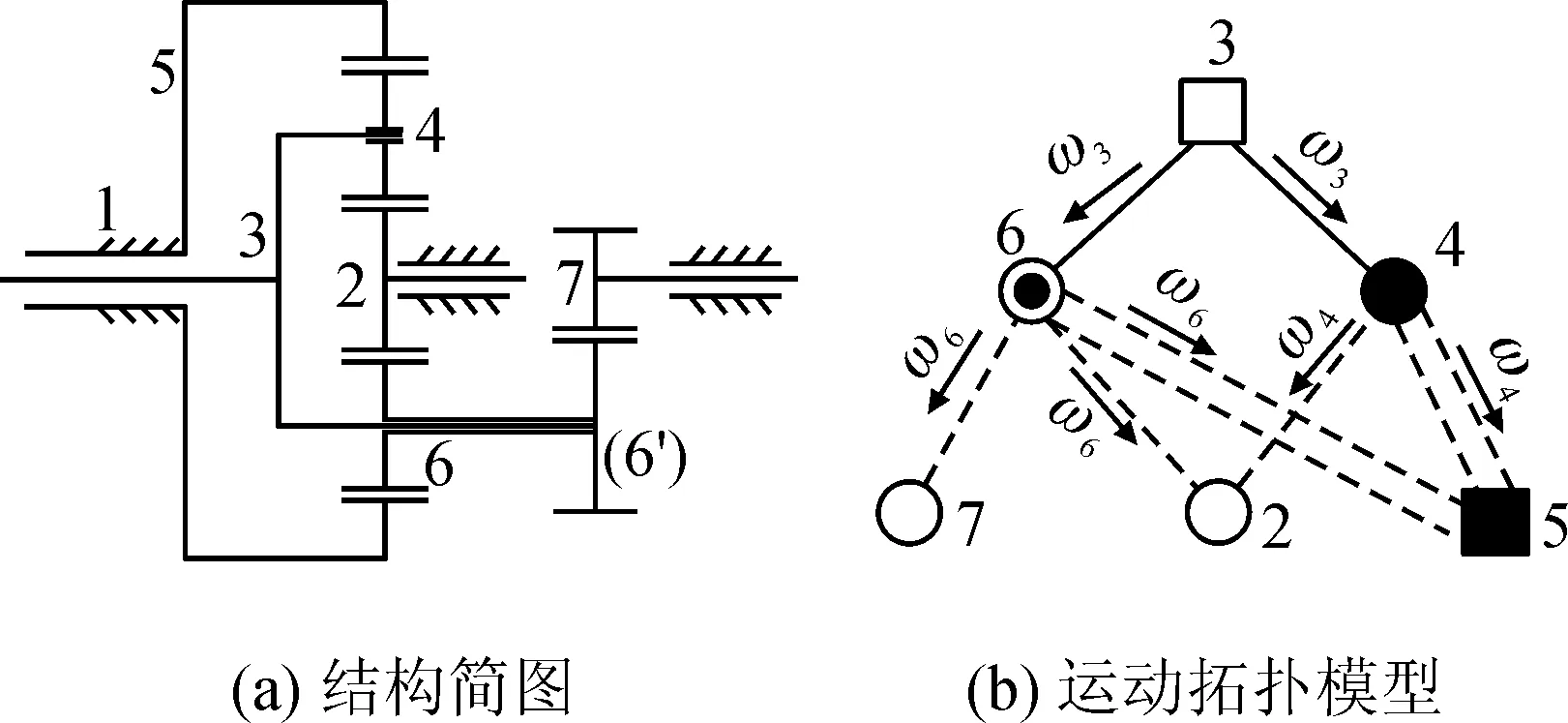
圖6 復式行星齒輪傳動機構

根據圖6(b)中的運動拓撲模型可知，其基本運動單元為：1(3-4-5)、2(3-4-2)、3(3-6-5)、4(3-6′-7)。根據式(5)，建立輪系的角速度約束方程：

(6)

式中：ωin表示復式行星架的輸入角速度。將式(6)寫成矩陣的形式：

(7)

倘若取復式太陽輪2、復式行星輪4、復式雙聯行星輪6和6′、復式內齒圈5和太陽輪7的齒輪齒數分別為Z2=12、Z4=14、Z5=40、Z6=14、Z6′=16和Z7=20，復式行星架的輸入轉速ωin=18 r/min，則其轉速方程為：

(8)

根據非齊次線性方程組理論，利用MATLAB計算出各構件的轉速如下：ω2=78 r/min，ω3=18 r/min，ω4=-33.428 6 r/min，ω5=0 r/min，ω6=-33.428 6 r/min，ω7=59.142 9 r/min。傳動比i=ω7/ω3=3.285。分析結果與轉化機構法計算的結果一致[22]。

4 結 論

在現有的研究成果基礎上，提出了描述多級行星輪系結構特征與運動特性信息的新圖形符號表示，基于新圖形符號建立了多級行星齒輪的結構拓撲模型和運動拓撲模型，實現了多級行星齒輪機構與拓撲模型的一一對應關系。運動拓撲模型揭示了組成運動回路的各構件之間的運動關系和系統整體的運動特性，根據行星輪系的基本運動單元，并結合非齊次方程組理論快速簡潔地求出輪系中各個運動學參量，有利于對行星輪系傳動性能系統化的研究。該圖形描述方法能夠清晰且完整地表達各構件的屬性和拓撲關系，將計算機無法識別儲存的行星齒輪機構轉換成可識別儲存的數字鄰接矩陣，有利于進行行星輪系的創新和綜合。