局部存水空間對寒區隧道襯砌劣損特性的影響分析

馬云峰，徐林生

(1. 重慶交通大學 土木工程學院， 重慶 400074； 2. 重慶水利電力職業技術學院，重慶 402160)

寒區隧道在修筑建設方面面臨的技術問題較一般地區復雜得多，其中一個關鍵性的問題就是凍融和凍脹的影響[1]。在我國的寒區隧道中，非多年凍土隧道是分布最為廣泛的一種，此類隧道多數圍巖凍脹性很弱或是沒有凍脹性，簡單地用“隧道襯砌在圍巖凍脹作用下開裂破壞”來解釋寒區隧道凍害產生的原因是不準確的。在此類寒區隧道中，襯砌背后積存的水體凍脹引起的襯砌凍脹壓力是造成凍害的主要原因。由于寒區隧道在開挖過程中開挖面的不規則性導致施工過程中常常沒有做到圍巖和襯砌結構緊密地貼合在一起，而是在襯砌和圍巖之間留下局部存水空間。這種空間大多數存在于拱頂部位，主要是由混凝土澆筑工藝和混凝土在水化過程中自身體積變形引起的。

近年來，學者們除了對隧道圍巖凍脹作用的影響進行了大量研究外，對隧道襯砌的凍脹破壞規律也進行了多方面的研究。王亞偉等[2]建立了兩種襯砌背后空洞積水的凍脹簡化模型，并對襯砌背后凍脹力的內力影響規律以及誤差進行定量分析；李巖松等[3]利用復變函數理論引入一種求解考慮襯砌背后空洞積水的凍脹力和凍脹變形的方法；高焱等[4]利用室內模型試驗，對隧道襯砌背后不同積水位置和積水體積的凍脹影響進行了分析。

本文在前人研究的基礎之上，根據局部存水空間的特點，建立了水熱力耦合凍脹模型，在驗證模型可行性的基礎上，通過數值模擬研究了襯砌存水空間作用位置、凍脹量等因素影響下，襯砌的應力變化及裂縫產生的部位、擴展的狀態和分布的規律。

1 水熱力三場耦合理論

1.1 基本假設

為了便于對劣損狀態進行量化分析，做出假設：

1) 存水空間內的未凍土視為各向同性材料；

2) 不考慮水分由液態轉向固態過程中熱量的遷移；

3) 水變為冰的壓力值不變。

1.2 三維非穩態熱傳導方程

根據熱力學第一定律及傳熱學基本理論，存水空間內部溫度變化遵循能量守恒定律，化簡非穩態熱傳導方程可得[5]：

(1)

式中：T為存水空間溫度；t為時間；α為襯砌的熱擴散率；qv為單位時間內單位體積放出的熱量；γ為襯砌的容重；c為襯砌的熱擴散率。

1.3 溫度場的離散化

在存水空間范圍Ω，采用伽遼金法和加權殘余法對熱傳導方程進行離散[6]：

(2)

式中：W為權函數；λ為襯砌的導熱系數。

1.4 三維水分遷移控制方程

本文以壓力水頭來描述水分遷移的驅動力，以液態水的總體積來描述水分遷移的過程，根據質量守恒定律，遷移的過程遵循達西定律，最終簡化的水分遷移微分方程為[7]：

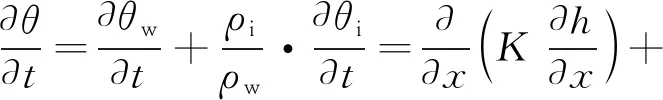
(3)

式中：θ為總體積含水量；θw為液態水體積含量；θi為含冰量；h為壓力水頭；K是非飽和土體內導水系數；ρw和ρi分別為水和冰的密度。

1.5 應力應變控制方程

1) 平衡微分方程

(4)

2) 幾何方程

(5)

3) 物理方程

(6)

4) 當T<0 ℃時

(7)

式中：f為體應力；σ為正應力；τ為切應力；E為彈性模量；μ為泊松比；ε為正應變；?u為位移矢量；εwi為溫水耦合作用產生的應變。

2 ABAQUS有限元數學模型

2.1 定義形函數

(8)

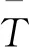
將式(8)代入式(2)中得到溫度-滲流耦合方程(9)，通過ABAQUS的求解器可以得到中心區域內節點的溫度值。

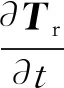
(9)

式中：Tr為溫度列矩陣。

(10)

式中：β為介質表面的放熱系數；Ta為外界溫度；s是襯砌和存水空間的接觸面積；e為存水空間和襯砌的集合。

在存水空間中隧道襯砌的凍脹破壞主要是由水體凍脹引起的體積變化而產生[8]，根據應變增量法以及上述節點的溫度值，按式(9)計算由蠕變和體積膨脹引起的等效節點荷載：

(11)

式中：Δ{εc}為蠕變應變增量矩陣；Δ{εv}為膨脹變形增量矩陣；v為存水空間范圍；[B]為單元形函數；[D]為襯砌溫度相關的塑性矩陣；結冰時，Δ{R}取正，融化時，Δ{R}取負。

2.2 定界條件

2.2.1初始條件

(12)

式中：Ti(i=r,w)分別為襯砌溫度場的初始條件和存水空間內水流溫度場的初始條件；T0為邊界溫度。

2.2.2邊界條件

(13)

式中：n為法向；s(x,y,z,t)是接觸面的表面積；λi(i=r,w)分別表示襯砌的導熱系數和存水空間內水體的導熱系數。

2.2.3邊界耦合條件

襯砌和存水空間的交界面是耦合面，需滿足以下兩個條件[9]：

(14)

3 數值模型的可行性分析

數值模型以國道316線江洛鎮至天水段八盤山隧道的主洞為原型。計算中為了凸顯局部存水空間對隧道二次襯砌劣損性的影響，本文的數值模擬不考慮隧道埋深對隧道襯砌結構開裂的影響，主要考慮襯砌混凝土壓潰、拉裂以及裂縫的延展導致的襯砌承載力失效。襯砌裂縫的擴展準則采用最大主應力失效準則[10]。數值模擬中采用ABAQUS中的XFEM模塊模擬襯砌開裂，此法無需對裂縫進行預設，嵌入的cohesive單元層不依賴網格，可以模擬多裂縫的擴展和擴展速率。隧道襯砌網格采用六面體結構劃分，單元類型為3D應力減縮積分單元，并在存水空間位置處網格加密，共劃分單元65 654個，采用彈簧單元模擬圍巖抗力。數值模型熱物理學參數和襯砌的物理力學參數如表1、2所示。

表1 數值模型熱物理學參數

表2 數值模型襯砌物理力學參數

八盤山隧道采用復合式襯砌，襯砌厚度為60 cm，隧道內輪廓為曲墻式等截面三心圓，拱頂高7.0 m，凈寬10.5 m。結合長期的監控數據以及2018年八盤山隧道維修完善工程數據顯示，該隧道襯砌環向裂縫23處，其中環向貫通裂縫約4處，縫寬在0.1～5.0 mm之間，縫長(除環向貫通裂縫)在10～130 mm之間，環向裂縫大部分存在滲水泛堿現象；襯砌縱向裂縫10處，其中邊墻縱向裂縫4處，縫寬在0.2～0.3 mm之間，拱腰及起拱線縱向裂縫6處，縫寬在0.2～0.5 mm之間；襯砌斜向裂縫15處，縫寬在0.2～0.6 mm之間，縫長在5.0～16.0 m之間，斜向裂縫大部分存在滲水泛堿現象；襯砌交叉裂縫2處，主要集中于拱頂及邊墻位置，裂縫寬度在0.2～0.5 mm之間，交叉裂縫均存在滲水泛堿現象。基于以上八盤山隧道襯砌裂損狀況，選取其中一個監測斷面，通過地質雷達和投入式靜壓液位計探明了該斷面在拱頂處有存水空間，并探明了空間水體的位置和大小。為了驗證數值模型模擬多場耦合作用下襯砌劣損的規律和適用性，選取拱頂處空間水體為類橢球體的工況進行對比驗證。其中，模擬的類橢球體水體空間的靜壓和液面高度與實測存水空間相同。驗證結果如圖1、2所示。

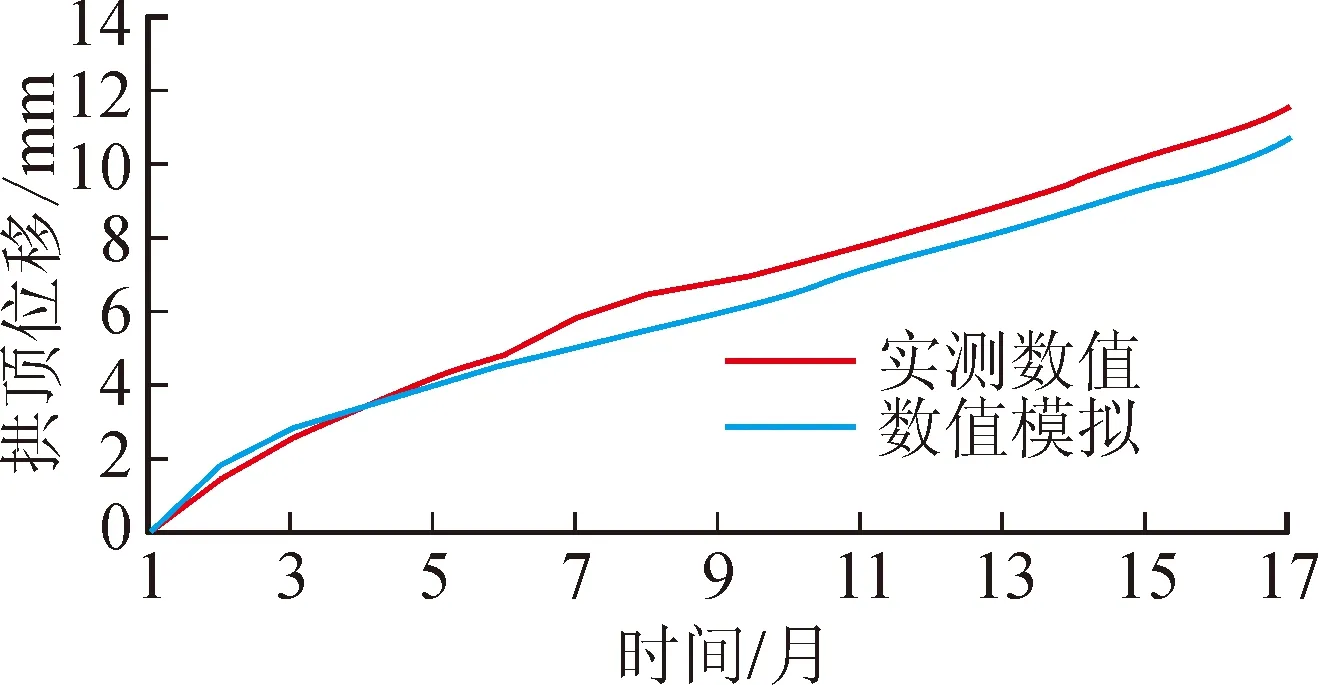
圖1 數值模擬與監控數據的拱頂時間-位移曲線

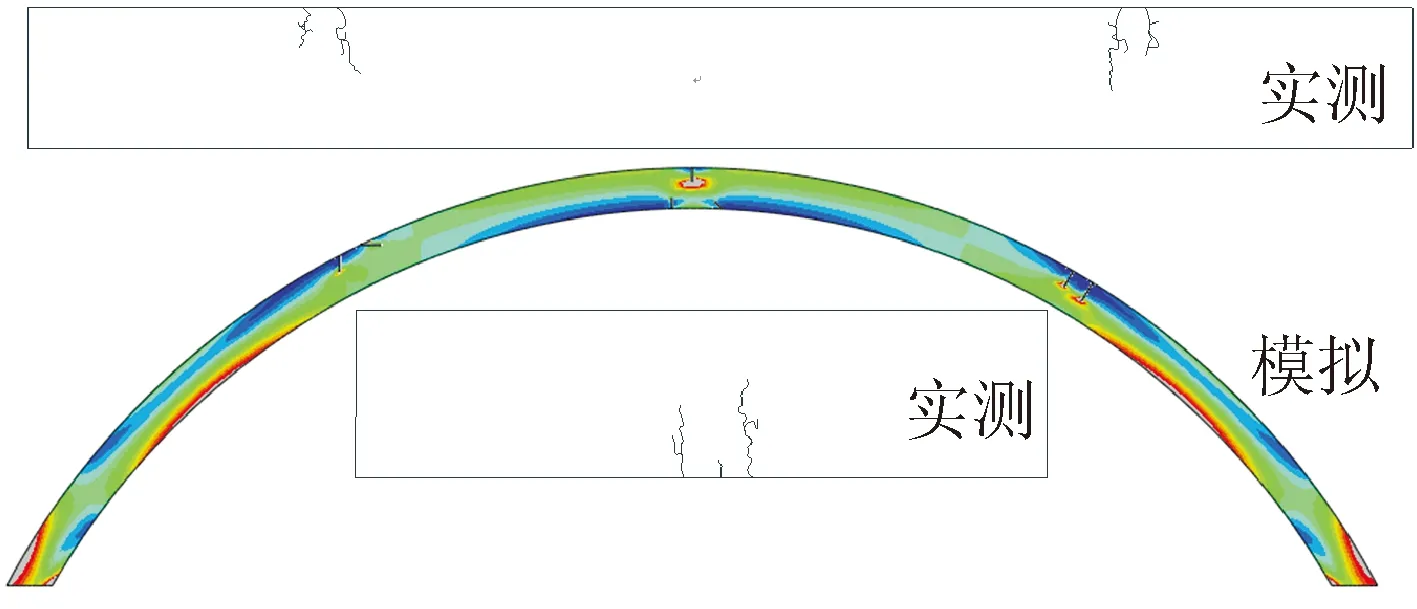
圖2 數值模擬與實際監控裂縫分布狀態對比圖

圖1、2分別是數值模擬與現場實測得到的拱頂沉降位移對比曲線和襯砌裂縫分布狀態圖。通過對17個月的拱頂位移值進行對比分析，結果顯示實測數值較模擬數值略高，二者平均值差值低于實測值的5%，并且兩數值曲線的拱頂位移擴展趨勢基本一致。圖2分析結果顯示，從裂縫的分布狀態和位置上看，二者的結果基本一致，并且實測裂縫的特征與數值模擬基本相同，內表面裂縫呈現出張拉特性，外表面呈現剪壓特性。由此可見，采用本模型來模擬寒區隧道襯砌的劣損性是可行的。

4 寒區隧道局部存水空間的數值模擬

為了便于模型收斂計算，將存水空間假定為半橢球體，數值模擬的過程不考慮溫度變化對襯砌結構應力的影響，只計算局部存水空間產生的凍脹附加應力和凍融循環對二次襯砌劣損性的影響。圖3為局部存水空間的計算示意圖。

圖3 局部存水空間計算示意圖

4.1 存水空間位置對隧道襯砌劣損性的影響

考慮到隧道工程實際存水空間所在的位置，本文僅就拱頂、拱腰、拱腳和仰拱四處范圍內的存水空間對襯砌劣損狀態的影響進行分析。采用溫度線性的加載方式對四種工況下裂縫的擴展狀態進行對比分析，如圖4所示。

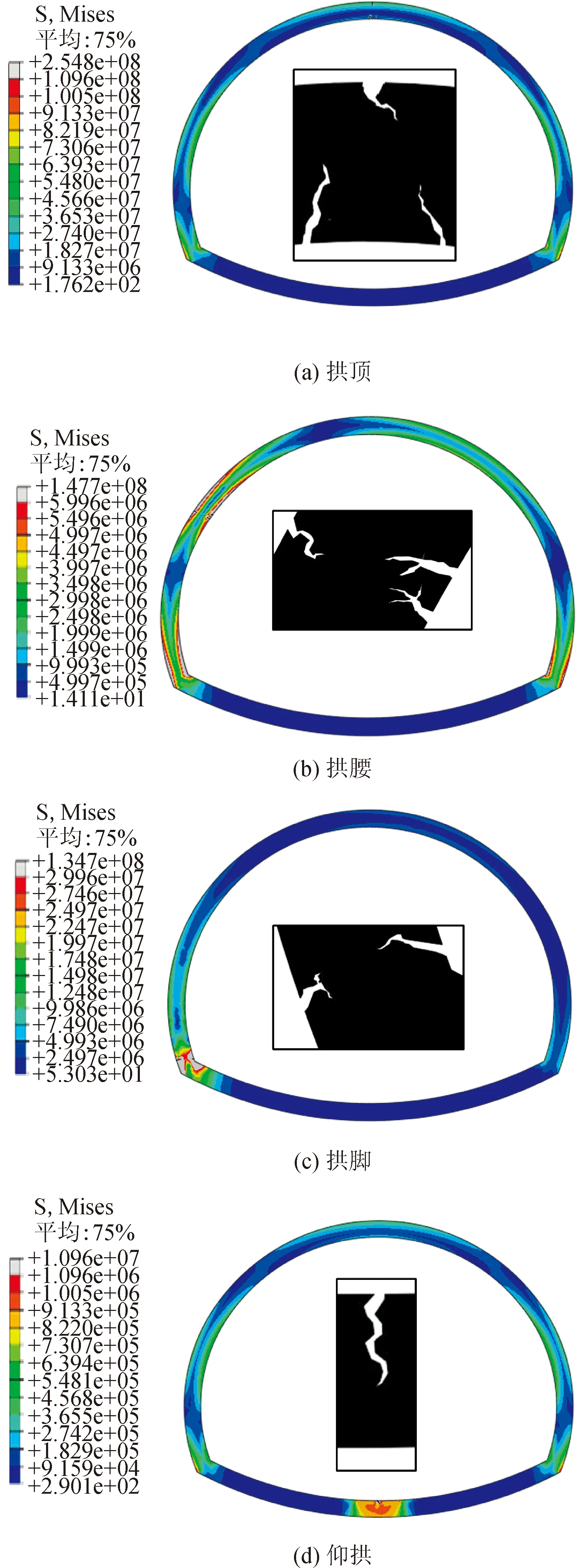
圖4 局部存水空間作用裂縫分布狀態圖

由圖4可以看出，四種工況下，產生裂縫的范圍都集中在存水部位附近，并且在對應襯砌內表面位置均表現出明顯的張拉特性；另外，在拱頂、拱腰和拱腳部位出現了不同程度的壓潰型裂縫的起裂。拱頂位置在凍脹過程中內表面出現了較多裂縫，在開裂的過程中，裂縫的狀態出現了起裂到閉合到再次開裂的情況，這表明襯砌在受力過程中呈現了剪拉交替的狀態，這種狀態除了出現明顯的剪切破裂面外，同時還伴隨著多處拉伸破壞線，這將極大地加速襯砌的劣化損傷進程。拱腰存水部位的凍脹也是一種偏壓的作用，襯砌內表面的裂縫主要以張開為主，伴隨著溫度荷載的不斷增加，裂縫的外觀形式呈現出“X”狀。拱腳處軸力和彎矩增大的過程中，軸力的增長速率大于彎矩的增長速率，呈現以軸力為主導，裂縫的擴展速率降低。仰拱存水部位在凍脹過程中在襯砌內表面出現一處延豎直方向擴展緩慢的裂縫，在襯砌的外表面出現了壓力集中現象。

圖5為襯砌裂縫開裂前后應力的分布狀況，其中拱頂存水對襯砌劣損的影響最大。隨著溫度的降低，從應力的增長速率和裂縫的擴展速率上看，由大到小分別是拱頂、拱腰、拱腳、仰拱。

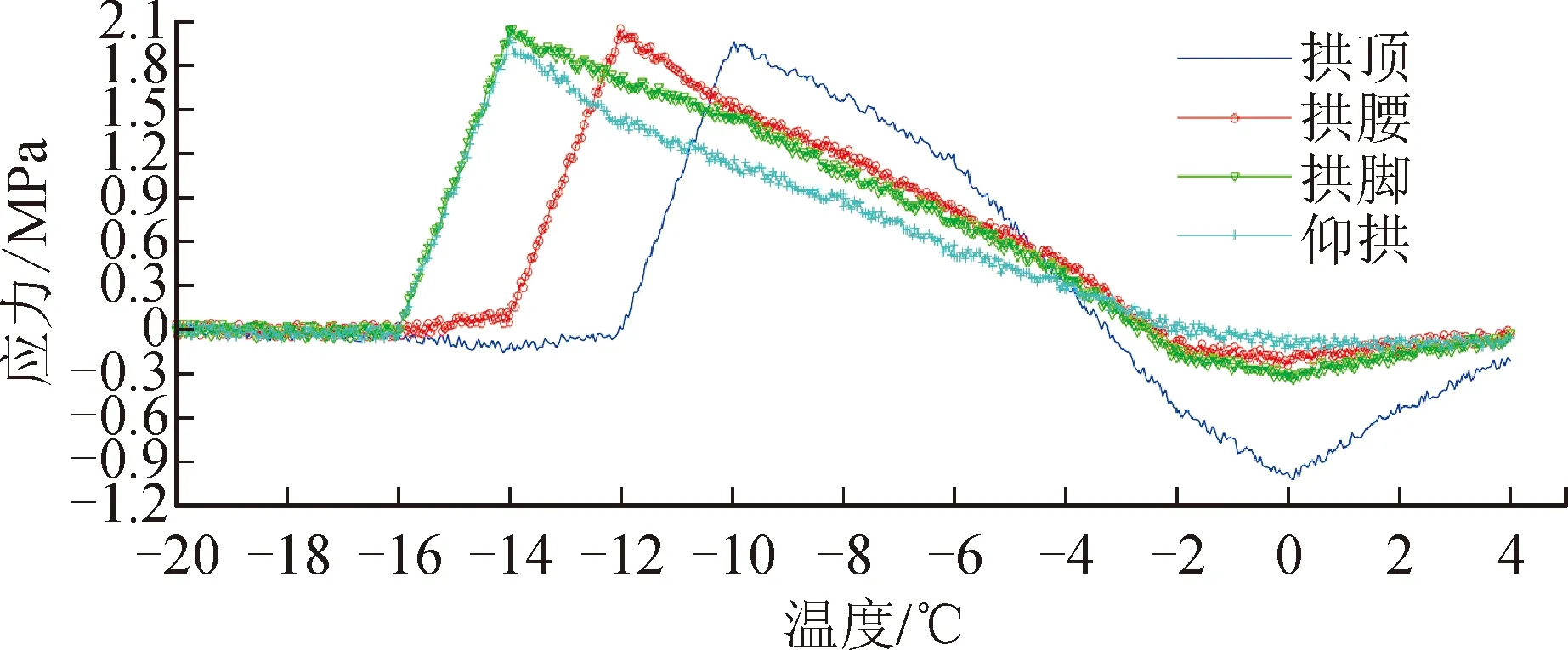
圖5 裂縫開裂前后的應力分布規律

4.2 凍脹量對隧道襯砌劣損性的影響

為了描述寒區隧道襯砌的劣損性，選取拱頂凍脹量進行量化描述：

h=fZd

(15)

式中：h為凍脹量；f為拱頂平均凍脹強度；Zd為凍結面至襯砌外表面的法向距離。

八盤山隧道拱頂監測段數據顯示，最大凍脹量約為6.7 mm，此時頂板溫度為-12 ℃。本文分別在凍脹量為2 mm、4 mm、6 mm、8 mm四種工況下，分析存水空間對隧道襯砌裂縫的分布及開裂規律的影響，如圖6所示。

由圖6可見，當凍脹量為2 mm時，并未出現明顯開裂跡象，但是襯砌內表面存在受壓集中現象。當凍脹量達到4 mm時，襯砌的內表面出現開裂跡象，外表面的受壓集中區域表現明顯。當凍脹量增加到6 mm時，在襯砌內表面出現一處主裂縫且擴展較快，襯砌外表面有輕微壓潰現象。當凍脹量繼續增大到8 mm時，襯砌裂縫的分布發生變化，在拱腰附近的內外表面也出現多裂縫的擴展，拱頂出現局部壓潰。由于拱頂內表面裂縫的持續擴展導致襯砌結構失效。

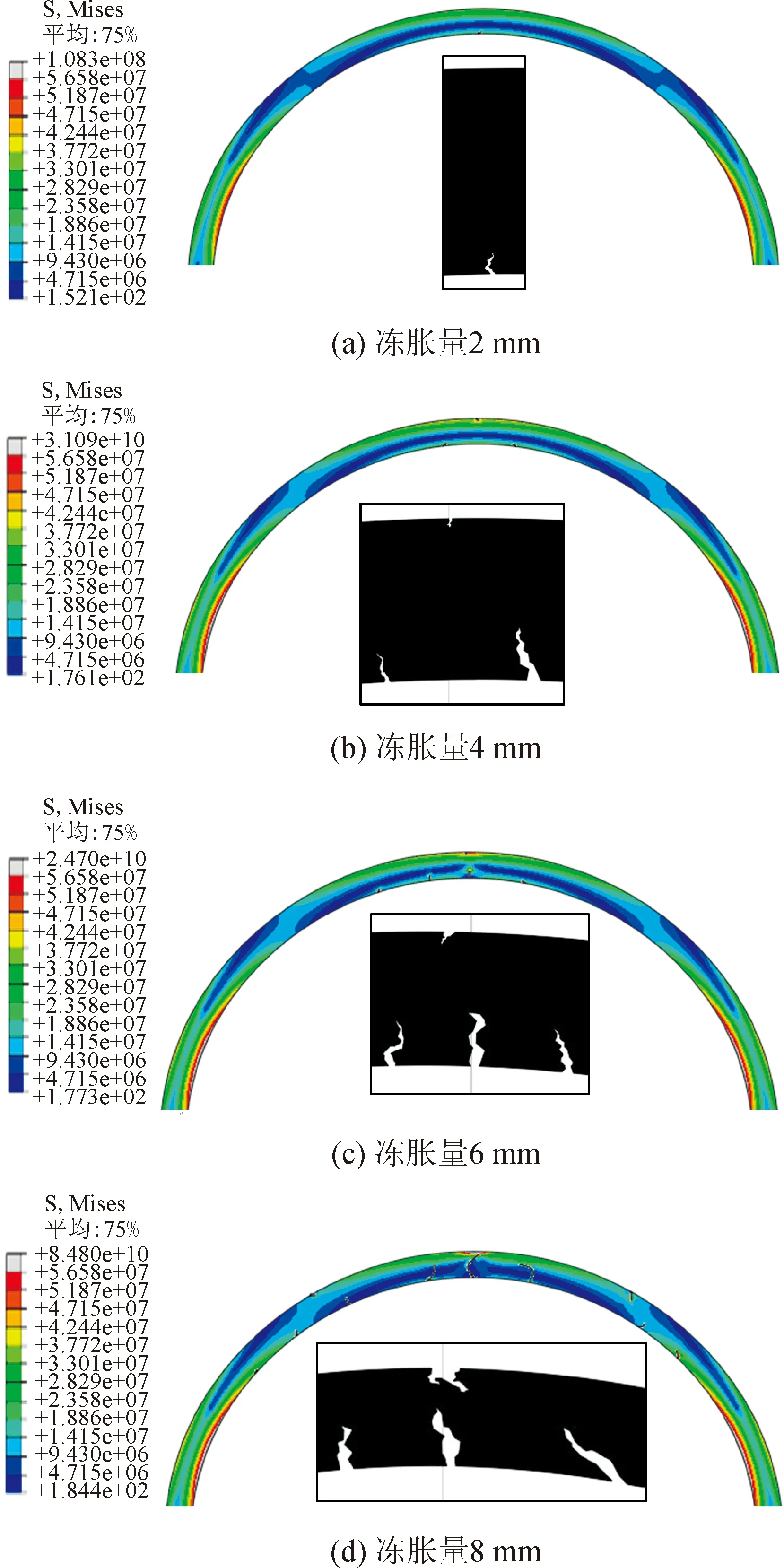
圖6 不同凍脹量襯砌裂縫的開裂狀態

凍脹量對襯砌應力的影響效果顯著，同一凍融周期內，襯砌應力隨著凍脹量的增長而增長。考慮到襯砌8 mm的凍脹量存在時間較短，分析24天內不同凍脹量下襯砌的開裂情況。

圖7給出了襯砌拱頂內表面裂縫開裂前后的應力分布規律，在裂縫逐步擴展的過程中，襯砌內表面主要承受拉應力的作用，裂縫主要表現出張拉特性。應力的增長速率和裂縫的擴展速率隨著凍脹量的增加而增大。

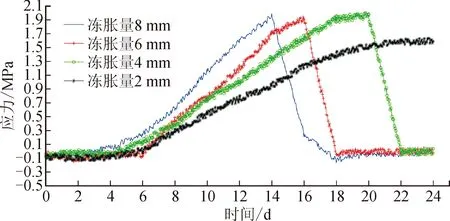
圖7 拱頂裂縫開裂前后的應力分布規律

4.3 襯砌厚度變化對隧道襯砌劣損性的影響

本文以八盤山隧道襯砌厚度55 cm為基本模型、襯砌厚度30 cm為襯砌厚度不足模型、襯砌厚度70 cm為襯砌厚度增強模型，隧道的外徑不變，分析拱頂在6 mm凍脹量狀態下襯砌的劣損性，如圖8所示。

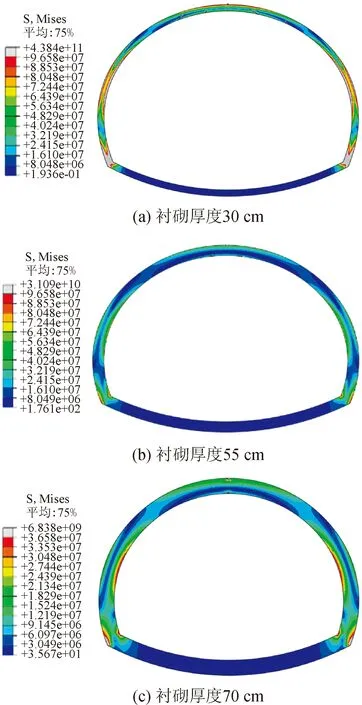
圖8 不同襯砌厚度裂縫開裂狀態

從圖8中可知，在凍脹量加載的過程中，三種模型開裂的位置均分布在襯砌內表面，并呈現張拉特性。其中，襯砌厚度30cm模型產生的裂縫數量較多、寬度較大，裂縫的擴展范圍從拱頂延伸至拱肩位置。

為了更好地反映襯砌厚度不足情況下襯砌的漸進劣損狀態，輸出整個模型的歷程變化曲線如圖9所示。在整個凍脹量加載過程中，55 cm和70 cm厚度襯砌應變能變化較為平緩，裂紋擴展基本處于穩態階段；而30 cm厚度襯砌在凍脹量加載中后期，其曲線出現斷層式跳躍并以更大的斜率不斷增長，說明在此階段裂縫已經進入擴展狀態，并且裂縫在襯砌周身大面積擴展，襯砌的承載性能大幅度下降。

圖9 整個襯砌應變能釋放的歷程曲線

5 結 論

1) 通過對檢測監控數據的對比分析，本模型適用于模擬寒區隧道襯砌劣損開裂與裂縫擴展過程的量化分析研究。

2) 存水空間作用下，隧道襯砌結構在存水空間對應的中心區域產生的裂縫較為集中，且多表現為張拉型裂縫。從開裂前后的應力變化及裂縫的擴展狀態來看，襯砌的劣損狀態由強到弱分別為拱頂存水、拱腰存水、拱腳存水、仰拱存水。

3) 凍脹量的大小對隧道襯砌的應力和裂縫的擴展影響顯著，隧道襯砌的劣損性隨著襯砌凍脹量的增大而增大。

4) 與正常襯砌工況和加厚襯砌工況相比，在隧道襯砌厚度不足情況下，裂縫的擴展速率較快，應力的增長速率較大，并且整個襯砌產生的應變能遠大于正常襯砌模型。