Calculations of atomic polarizability for beryllium using MCDHF method?

Hui Dong(董輝), Jun Jiang(蔣軍),?, Zhongwen Wu(武中文), Chenzhong Dong(董晨鐘), and Gediminas Gaigalas

1Key Laboratory of Atomic and Molecular Physics and Functional Materials of Gansu Province,College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China

2Institute of Theoretical Physics and Astronomy,Vilnius University,Saul˙etekio Avenue 3,Vilnius 10222,Lithuania

Keywords: polarizabilities,MCDHF,blackbody radiation shift

1. Introduction

The knowledge of polarizabilities of atoms and ions is required in different areas of physics and chemistry,such as parity non-conservation in atoms,[1–3]optical atomic clocks,[4,5]blackbody radiation (BBR) shift in clock transitions,[6–8]and long-range interatomic potentials.[1,9]In the past three decades, the polarizabilities for the atoms with single- or double-valence electrons(group IA and group IIA)have been widely calculated by using many-body perturbation theory(MBPT),[1,10]relativistic coupled-cluster(RCC)theory,[11–15]relativistic and non-relativistic configuration interaction plus core polarization(CICP)methods.[16–19]

Most of these calculations are based on sum-over-states and finite-field approach. The sum-over-states approach is regarded as feasible for monovalent or divalent atoms to explicitly construct a set of intermediate states that is effectively complete. In the finite-field method, a set of equations are obtained by calculating the energies of atoms under different external field intensities, or polynomial fitting is used to obtain the polarizability. This is a simple and effective method to solve the polarizability, but it needs a lot of eigenstates. However,the sum-over-states and finite-field approach are computationally more difficult to apply to multi-valenceelectron atoms, since the larger dimensions involved would preclude an explicit computation of the entire set of intermediate state wavefunctions.[1]Therefore,the polarizabilities for much more complex multi-valence-electron atoms, rare gas,and halogen atoms,as well as highly charged ions,are insufficient owing to complex calculations.

The fully relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF) method is a very good method to calculate the atomic parameters of multi-valence-electron atoms.Through nearly 40 years of development, the new package of GRASP2018[20]has been upgraded to a powerful software. It includes a number of tools to calculate the relativistic wavefunctions, energy levels,[21]hyperfine structure(HFS),[22]isotope shifts(IS),[23,24]Land′e g-factors,[21,25]transition probabilities[26,27]for the multi-valence-electron and multi-open subshell atoms. Therefore,it is a good way to calculate the polarizabilities of complex atomic systems based on the MCDHF method and the corresponding GRASP2018 program.[20]

Beryllium has many important applications in studying complex atom theory, such as fine-structure constant,[28,29]quantum information,[30]and extracting nuclear information.[31,32]Moreover, beryllium is a relatively simple multi-electron atomic system. In the present work,a program for calculating the polarizabilities based on the GRASP2018 package[20]has been developed. As the first application, the transition energies, electric-dipole (E1) matrix elements, and E1 polarizabilities of the ground state 2s21S0and excited state 2s2p3P0for beryllium are calculated. Then the BBR shift for the 2s2p3P0→2s21S0clock transition is determined. Our results are compared with some available experimental and theoretical results in detail.

2. Theoretical method

In the MCDHF method,the atomic state functions(ASF)are written as a linear combination of configuration state functions(CSF)

In the present work, we first calculate the wavefunctions of the ground state(1s22s2)by using the Dirac–Hartree–Fock(DHF)method.In order to get excited orbitals with a very high principal quantum number n, we do not use GRASP2018 to generate the excited orbital wavefunctions. Instead,the orbital wavefunctions are written as the linear combinations of analytical S-spinors and L-spinors,[33]and generated by solving the single-electron Dirac equation in which the Hamiltonian is written as

And then, the analytical single-electron orbital wavefunctions are converted into numerical form to match the GRASP2018 package. Finally, the electron correlation effects are considered in detail by using the active-space method.[35,36]

The static scalar electric-multipole polarizability for a given atomic state i can be calculated by using the sum-overstates method,that is

According to the Wigner–Eckart theorem

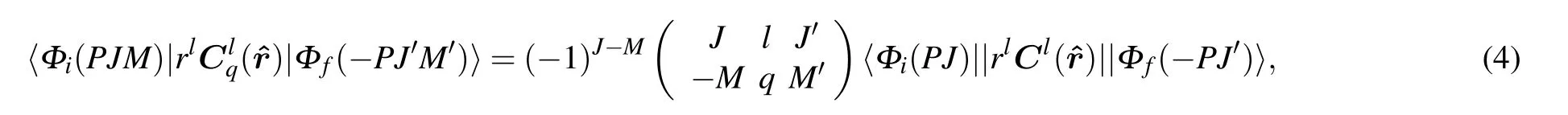
where q=0,±1,Eq.(3)can be written as

Assuming a pseudostate

Applying the operator(Ei?H)onto the two sides of Eq.(6),we obtain

where H is the Hamiltonian operator of atomic system.

According to the identity transformation operator

where Φm(γ)represents all additional states in addition to the states Φf,and γ denotes the corresponding quantum numbers.Substituting Eq.(9)into the right side of Eq.(8)gives

Applying the Wigner–Eckart theorem,Eq.(13)is simplified to

and Eq.(14)is simplified as

The E1 polarizabilities of the J=0 states can be obtained by solving Eqs.(16)and(17).

3. Results and discussion

In order to show the wavefunctions we calculated, the transition energies ?E and E1 reduced matrix elements D for some principal E1 transitions are listed in Table 2. It can be found that the transition energies tend to converge and the variations are less than 0.02% for core-valence correlation.Compared with the national institute of science and technology(NIST)tabulation,[38]the differences between our results and the NIST results are less than 4%. The contribution of valence-valence correlation accounts for more than 95%, and that of core-valence correlation is less than 5%.

For the 2s21S0→2s2p3P1recombination line, the E1 matrix element is very small. After considering the corevalence correlation, our result 2.327×10?4a.u. is in good agreement with the NIST’s result 2.429×10?4a.u.[38]For the 2s21S0→2s2p1P1and 2s3p1P1resonance lines,the E1 matrix elements are relatively large. The present matrix elements tend to converge, and the variations are less than 0.2%. The present results agree with those of NIST,[38]experiments[41,42]and other theoretical results of multiconfiguration Hartree-Fock(MCHF),[39]CICP[18]and MBPT[40]methods very well.

Table 2. Transition energies ?E (in Hartree) and E1 reduced matrix elements D (in a.u.) for the transitions from the 2s21S0 and 2s2p 3P0 states of beryllium.

For the 2s2p3P0→2s3s3S1,2p23P1,2s3d3D1,and 2s4s3S1transitions, the presently calculated E1 matrix elements tend to converge and the variations are less than 0.5%. The differences between the present results and NIST[38]results are less than 1%.

Using these obtained wavefunctions, E1 reduced matrix elements and Hamiltonian matrix elements in each correlation model, the polarizabilities for the 2s21S0and 2s2p3P0states are calculated by solving Eqs. (16) and (17) and listed in Table 3. For the 2s21S0state, the present result converges to 37.614 a.u., which agrees with the MCHF result 37.62 a.u.[43]excellently. It also agrees with other theoretical results[11,18,19,45,46,48–51]very well,and the differences are less than 1%. These differences are mainly caused by the difference in transition energies shown in Table 2 and completeness of the configuration space, without considering the triple excitations as well as the Breit interaction and QED effects. For the 2s2p3P0state, the present result converges to 39.249 a.u., which is also in good agreement with the theoretical results of MCHF[43]and CICP.[18]Actually, the nonrelativistic CICP and MCHF results are average polarizabilities of the 2s2p3P0,1,2states.

By means of these polarizabilities, the BBR shift for the 2s2p3P0→2s21S0clock transition is determined and listed in

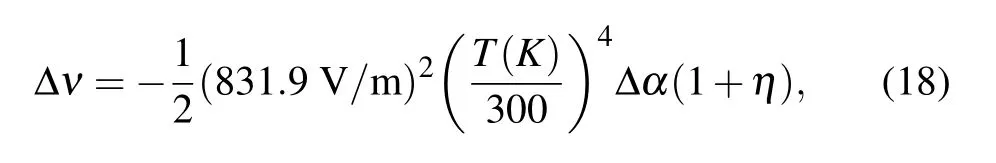
where ?α is the difference of static scalar polarizabilities of the 2s21S0and 2s2p3P0state.The factor η is a small dynamic correction that can be ignored.[52]T is the ambient temperature and set to 300 K in the present calculation.It can be found in Table 3,the BBR shift converges to 0.0141 Hz,which is in good agreement with the results calculated by using the CICP and MCHF polarizabilities.[18,43]This BBR shift is one or two orders of magnitude smaller than those of clock transitions for other alkaline-earth-metal atoms, such as 0.258 Hz for magnesium, 1.171 Hz for calcium, 2.354 Hz for strontium, and 1.25 Hz for ytterbium.[52]This character is of great significance to the study of beryllium atomic clocks.

Table 3. E1 polarizabilities α (in a.u.) for the 2s21S0 and 2s2p 3P0 states of beryllium. ?α (in a.u.) represents the difference of polarizabilities between 2s21S0 state and 2s2p 3P0 state. ?νBBR (in Hz)is the BBR shift for the 2s21S0 →2s2p 3P0 clock transition,and temperature T is equal to 300 K.

4. Conclusion

In summary, combining with the GRASP2018 package which is based on the MCDHF method,a program to calculate the polarizabilities is developed. As the first application, the transition energies, E1 matrix elements, and E1 polarizabilities for the 2s21S0and 2s2p3P0states of beryllium are calculated. The presently calculated polarizabilities are in good agreement with the results of other methods, and the difference is less than 1%. The BBR shift for the 2s2p3P0→2s21S0clock transition is further determined. The present result is also in good agreement with other theoretical results. The BBR shift for the 2s2p3P0→2s21S0clock transition of beryllium is one or two orders of magnitude smaller than that of other alkaline-earth-metal atoms.

In the following work,we will focus on studying the polarizabilities of more complex atoms and highly charged ions using this method. The study of E2,E3 and dynamic polarizability is also very important in atomic clocks and other fields.It is feasible to develop the dynamic polarizability program based on the existing program. We will continue to improve our performance in the next step. In addition, the Breit interaction and quantum electrodynamics(QED)effect can also be considered in the calculation of the static E1 polarizabilities.