基于灰色LS-SVM的裝備器材需求預測模型

賈 琦，楊 帆，王鐵寧

(1.陸軍裝甲兵學院， 北京 100072； 2.北部戰區陸軍， 濟南 250000；3.解放軍96901部隊， 北京 100095)

需求預測是裝備器材保障的重要環節，其準確性直接決定了器材保障工作的經濟效益和軍事效益[1]。隨著現代戰爭信息化程度的不斷升級，智能化決策的特點愈發凸顯。在裝備器材保障方面，裝備集成化、復雜化、智能化程度越來越高，新裝備不斷充實到基層單位，器材備件消耗規律的不確定性大大提升，對裝備器材的精確化保障提出了嚴峻考驗。

目前，我軍在裝備器材保障過程中對新裝備器材需求的預測分析思路主要有“回顧歷史”和“著眼未來”兩種。“回顧歷史”是指從器材的歷史消耗入手，分析裝備的器材消耗歷史數據，尋找出器材的消耗規律，進而推測未來需求；“著眼未來”是指從裝備的動用計劃情況入手，根據裝備的動用、維修和保養任務計劃量，預測出器材的未來需求。此外，在歷史消耗數據積累較少的情況下，還應盡量多方面考慮影響因素進行分析，以減小因歷史數據少而帶來的預測誤差。兩種分析思路分別從不同角度對器材需求進行預測，各有側重。本文將兩種分析思路相結合，如圖1所示。一方面對積累不多的歷史數據進行深入分析，在一定程度上總結消耗規律；另一方面綜合分析裝備動用、維修和保養計劃，力求提高預測的精準性，同時還考慮氣候和使用條件等外部環境因素的影響，通過綜合分析各影響因素之間的關系，并根據內外雙重影響因素對器材的需求進行預測。

由于新裝備的投入使用時間短，器材的消耗數據、裝備的動用和維修等歷史數據積累較少，且不同裝備在不同的使用環境中消耗規律不盡相同[2]，因此大樣本數據的預測方法[3-5]并不適用。目前廣泛應用的需求預測方法主要有平滑指數法[6]、BP神經網絡[7]、Bayesian方法[8]等，這些方法對于解決器材需求預測具備一定的優勢，但局限性也十分明顯，如神經網絡運算靈活性不高、Bayesian方法的穩定性較低等。由于影響器材需求的因素具有不確定性和復雜性，而任一單一模型都具有其明顯的局限性，也無法全面表達器材需求的影響因素和態勢，難以得到理想的預測結果。因此，有必要運用組合預測的思路方法，通過結合不同預測方法的優勢，得到較為滿意的預測結果。

圖1 本文需求預測思路曲線

基于此，本文將灰色模型和最小二乘支持向量機(leastsquares-support vector machine,LS-SVM)方法相結合，設計了一種針對消耗數據較少情況的裝備器材需求預測方法。

1 灰色模型

灰色系統理論[9]是一門研究信息部分清楚、并帶有不確定性現象的應用數學學科，它將一切隨機變量看作灰色量，并將隨機過程看作在一定范圍內、一定時間階段內發生變化的灰色過程。灰色系統理論的核心是灰色模型，灰色模型首先對樣本數據序列進行累加(或累減)操作，降低樣本數據中的隨機性影響，獲得變化規律較強的新序列，然后建立預測模型，最后將預測結果通過“還原”累減(或累加)得到樣本數據序列的預測值。該方法在處理“小樣本、貧信息”的問題上優勢明顯。

最常用的灰色GM(1,N)限于1個變量，但是裝備器材需求預測的過程中受多種因素的影響，并不適用于復雜規律的情形，因此不能僅從一個影響因素進行預測分析。本文采用改進狀態模型GM(1,N)，研究N個變量對一個變量的影響關系。GM(1,N)表示一階N個變量的動態預測模型，包括1個行為變量x1，N-1個因子變量xi，每個變量表示一個長度為m的數列，即xi={xi(1),xi(2),…,xi(m)}，其中i=1,2,…,N。設有N個變量的GM(1,N)模型的原始數據序列為：

(1)

建模步驟如下：

步驟1 對樣本數據序列X(0)做累加生成，獲得新的數據序列為：

(2)

步驟2 建立GM(1,N)的灰微分方程，表示為：

(3)

式中：a表示模型的發展系數；b表示模型的灰色作用量。

(4)

步驟4 求解GM(1,N)模型參數，其過程為：

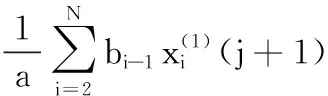
(5)

步驟5 數據累減還原，有：

(6)

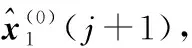
在裝備器材的需求預測過程中，由于多影響因素的互相作用極其復雜，數據列經過疊加后仍無法徹底消除其隨機特性，造成數據波動范圍較大等現象，嚴重影響預測的準確度，因此很多學者嘗試從不同角度分析歷史數值的殘差，并據此提高預測準確度[10-11]。

2 LS-SVM 模型

SVM作為一種精確預測方法[12]，是建立在統計學理論的VC維理論和結構風險最小原理基礎上的，根據有限的樣本信息在模型的學習精度(主要指對已有樣本的學習精度)和學習能力(主要指準確識別任意樣本的能力)之間尋求最佳折中[13]。SVM方法對于解決小樣本、非線性、不規則、不連續等具有獨特的優勢，其以超高的運算靈活度和較強的推廣能力，可以較完整地描述器材需求與影響因素之間的非線性關系，因而適用于小樣本數據的裝備器材需求預測。最小二乘支持向量機(LS-SVM)是對SVM方法的改進[14-15]，具有較強的非線性映射模仿能力，其以正則理論為基礎，可以實現將二次規劃問題轉化為求解線性方程組問題的過程，在提高收斂速度的同時可以提高預測的穩定性。

(7)

式中：γ表示調整參數；ω表示權重矩陣；b表示偏差值；ek表示誤差變量，ek∈R。

通過建立拉格朗日函數，并根據KTT條件，求解下列線性方程組：

(8)

由此得到LS-SVM回歸函數為：

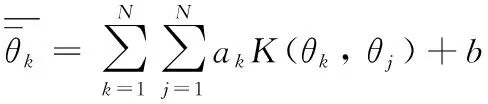
(9)

式中K(θk,θj)表示核函數。

3 灰色LS-SVM需求預測模型

根據以上分析可知，灰色模型的優勢在于能夠深入挖掘樣本數據之間的內在關系和變化規律，同時思路清晰，建模方便，存在的不足是不善于分析影響因素對外的作用及影響因素對預測結果的影響關系，同時在預測過程中無法完全避免數據的隨機性，容易造成預測結果的不穩定；而LS-VSM方法的優勢在于具有較強的泛化能力和穩定性，善于表多種影響因素對預測結果的影響關系，同時具有快速收斂和穩定性強的優勢。基于此，本文設計灰色LS-VSM需求預測模型，將LS-VSM引入到預測過程中，提高需求預測的準確性和穩定性。

在給出灰色LS-VSM需求預測模型之前，先對本文分析用到的各影響因素符號表示如下：

灰色LS-VSM需求預測模型構建步驟如下：

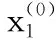
(10)

步驟2 通過引入GM(1,N)方法將原始數據序列X(0)進行一次累加計算，獲得規律性較強的新數據序列X(1)。

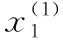
(11)

式中，σ2表示核函數的寬度。

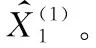
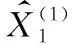
4 算例分析

假設有小樣本裝備器材Q對器材Q在2017和2018年間的器材需求量和相關影響因素數據作為樣本數據，如表1、表2所示，構建灰色LS-VSM需求預測模型(其中N=10,m=24)，對2019年1—6月器材需求量進行預測。

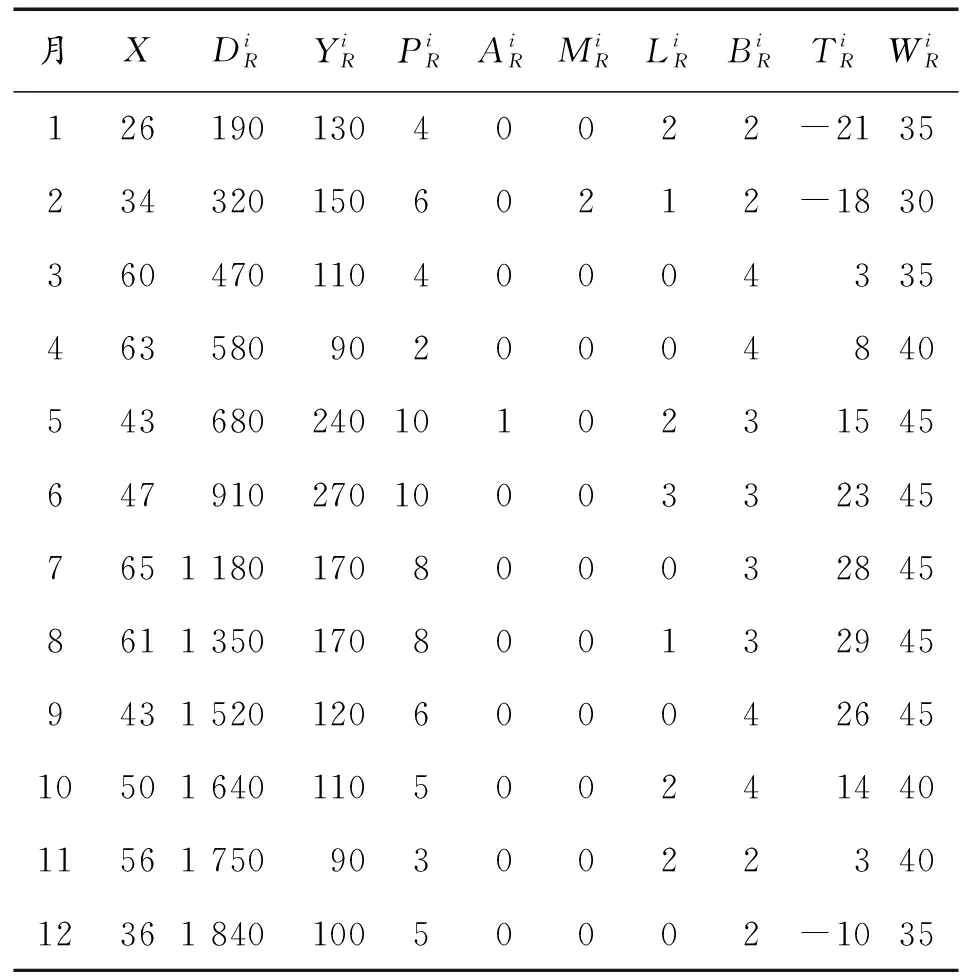
表1 2017年消耗參數

表2 2018年消耗參數

為了對比本文預測模型在小樣本數據器材需求預測的性能，將灰色預測LS-SVM模型預測結果與適用于大樣本數據的文獻[3]中的BP神經網絡方法，LS-SVM方法以及實際結果進行對比分析。3種方法的預測結果如圖2和表3所示，表3中APE為絕對百分比誤差(absolute percent error)，表示預測誤差大小，RMSE為均方根誤差(root mean square error)表示預測結果的穩定性，計算公式為：

(12)

(13)

其中，k表示月份(1—6)；N表示月份數(N=6)；y(k)表示第k個月的預測值；y0(k)表示第k個月的實際輸出值。

圖2 3種算法的預測數量曲線

從圖2可以看出，本文建立的灰色LS-SVM模型的預測曲線與實際需求曲線最接近，變化規律也最相似，而BP神經網絡模型對于小樣本數據的預測能力較差，與實際需求曲線相差最大。

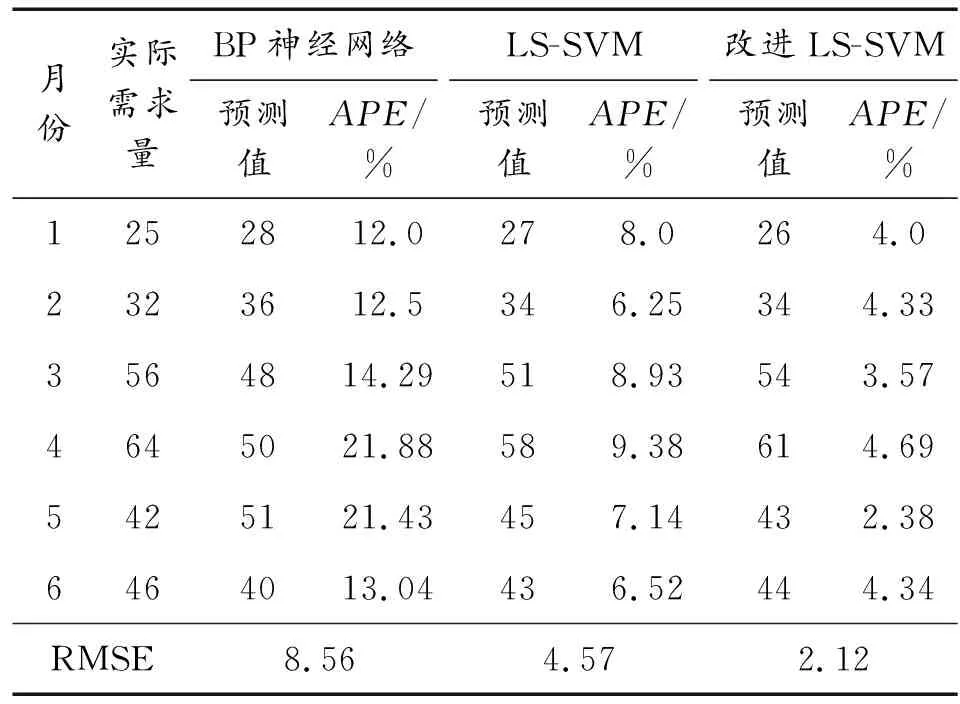
表3 3種方法的預測結果

分析對比表3的結果可知，BP神經網絡方法預測的APE范圍是12.0%～21.88%，RMSE值為8.56；傳統LS-SVM方法預測的APE范圍是6.25%～9.38%，RMSE值為4.57；本文提出的灰色LS-SVM方法預測APE范圍是2.38%～4.69%，誤差范圍最小，RMSE值為2.12，預測性能最穩定。結果表明適用于大樣本數據的BP神經網絡方法對于小樣本數據的需求預測精度較低，而灰色LS-SVM預測方法更加適用于小樣本器材的需求預測。

5 結論

1) 本文設計的灰色LS-SVM預測模型，具備灰色模型和LS-SVM模型的優勢，有較強的準確性和穩定性，能夠較好適應小樣本數據的裝備器材需求預測要求，說明灰色LS-SVM預測模型可行可用，尤其適用于使用時間較短的新型裝備。

2) 本文提出的灰色LS-SVM預測方法利用GM(1,N)方法對模型的輸入進行處理，并采用徑向基函數RBF作為核函數，但未對其他函數進行對應分析，下一步將針對不同核函數、不同參數對預測結果的影響進行全面深入分析。