原向反射式大靶面光幕探測靈敏度分布特性
高豐佳, 董 濤, 譚林秋, 陳 丁, 王 利
(1.西安工業大學 a.陜西省光電測試與儀器技術重點實驗室; b.兵器科學與技術學院, 西安 710021;2.中國兵器工業集團有限公司 黑龍江北方工具有限公司, 黑龍江 牡丹江 157000)
光幕測試技術作為兵器靶場測試的一個重要分支,廣泛地應用于各類身管武器測試領域中[1-3]。目前,各類光幕探測技術基本趨于成熟[4-5],例如,自帶光源的光幕靶[6]和采用天空背景光(也可配以室內光源)的天幕靶[7]均可用于室內、外的光幕探測,且測量原理簡單,精度較好。隨著新型身管武器裝備的不斷問世,其有效射程越來越遠,終點彈道散布也越來越大[8],現有光幕的有效探測靶面已無法滿足其測試要求,嚴重影響武器裝備的研制、調試以及試驗驗收周期。
為解決上述問題,相關研究人員提出了一些解決方案。例如,倪晉平,高芬等提出用90°廣角天幕靶搭配L形LED陣列光源構成直射式探測光幕[9],該方法的接收裝置直接使用了已有的廣角天幕靶,但發射裝置是多個光源的拼接,結構復雜,調節困難;趙冬娥等提出用原向反射玻璃裝置、半導體激光器、光電接收裝置構成反射式探測光幕[10],該激光光幕測速系統具有原理簡單,響應速度快的特點,但其探測靶面仍不能測試滿足需求;王芳等提出用原向反射膜、激光光學系統、全反射鏡、信號采集器等構成反射式探測光幕[11],這一裝置精度較高、使用維護方便、成本低,但光路中光能損耗較多,導致探測靈敏度較低。上述方法雖能擴展探測光幕面積,但仍存在結構復雜、探測靈敏度不足、設備裝調和移動不方便等一些問題需要解決。
因此,本文提出一種基于原向反射原理的大靶面光幕探測方法。由玻璃微珠與棱鏡結合的原向反射膜[12-13]、菲涅爾透鏡[14-15]、一字線激光器、光電轉換器件[16]等構成一個反射式矩形光幕探測系統。分析系統探測靈敏度分布特性并建立其模型,最后對該模型進行理論仿真與實驗驗證。
1 原向反射式光幕探測原理
圖1為提出的原向反射式大靶面光幕探測系統的原理示意圖,在系統右上方的靶架上貼上原向反射膜;將光電轉換器件安裝在菲涅爾透鏡的下方,保持兩者中心在同一豎直軸線上;將一字線激光器固定在菲涅爾透鏡的側面,保證一字線激光器的發光主點與菲涅爾透鏡的中心位置在同一水平軸線上;這三者整體構成收發裝置。然后將收發裝置旋轉,使之與水平面成45°夾角,并安裝在系統的左下方。
一字線激光器發出發散角θ=90°的扇形光源,該扇形光源投射到原向反射膜上,被其以一定的發散角近似原路反射回菲涅爾透鏡表面;菲涅爾透鏡接收到達其表面的光線并將光線聚焦到安裝在透鏡焦距處的光電轉換器件上;光電轉換器件接收光信號,將其轉化為電信號。當有彈丸穿過探測光幕時,會遮擋住一部分從激光器入射到原向反射膜上的光線,也會遮擋住一部分從原向反射膜反射回菲涅爾透鏡的光線,導致光電轉換器件接收到的光信號發生變化,從而其轉換成的電信號也發生變化,電路部分輸出變化后的電壓信號進而識別到彈丸。

圖1 系統原理示意圖
2 原向反射式光幕探測模型
如圖2所示,A點處一個很小的圓光斑被擴散為一字線光斑,擴散后的光斑在距離A點l處為曲面EFGH,相對于曲面的弧長,其寬度很小,因此,可以將EFGH近似看作矩形曲面,則其面積為:
SEFGH=EF·EH
(1)
如圖3所示,以A點為原點建立直角坐標系,原向反射膜上的任一點Q處坐標為(xQ,yQ),A點處的一字線光源發出發散角θ=90°扇形光幕,αQ為原向反射膜的入射光線與原向反射膜法線的夾角(即入射角);βQ為Q點處入射光線與被反射的出射光線夾角(即逆反射發散角)。
(2)
(3)

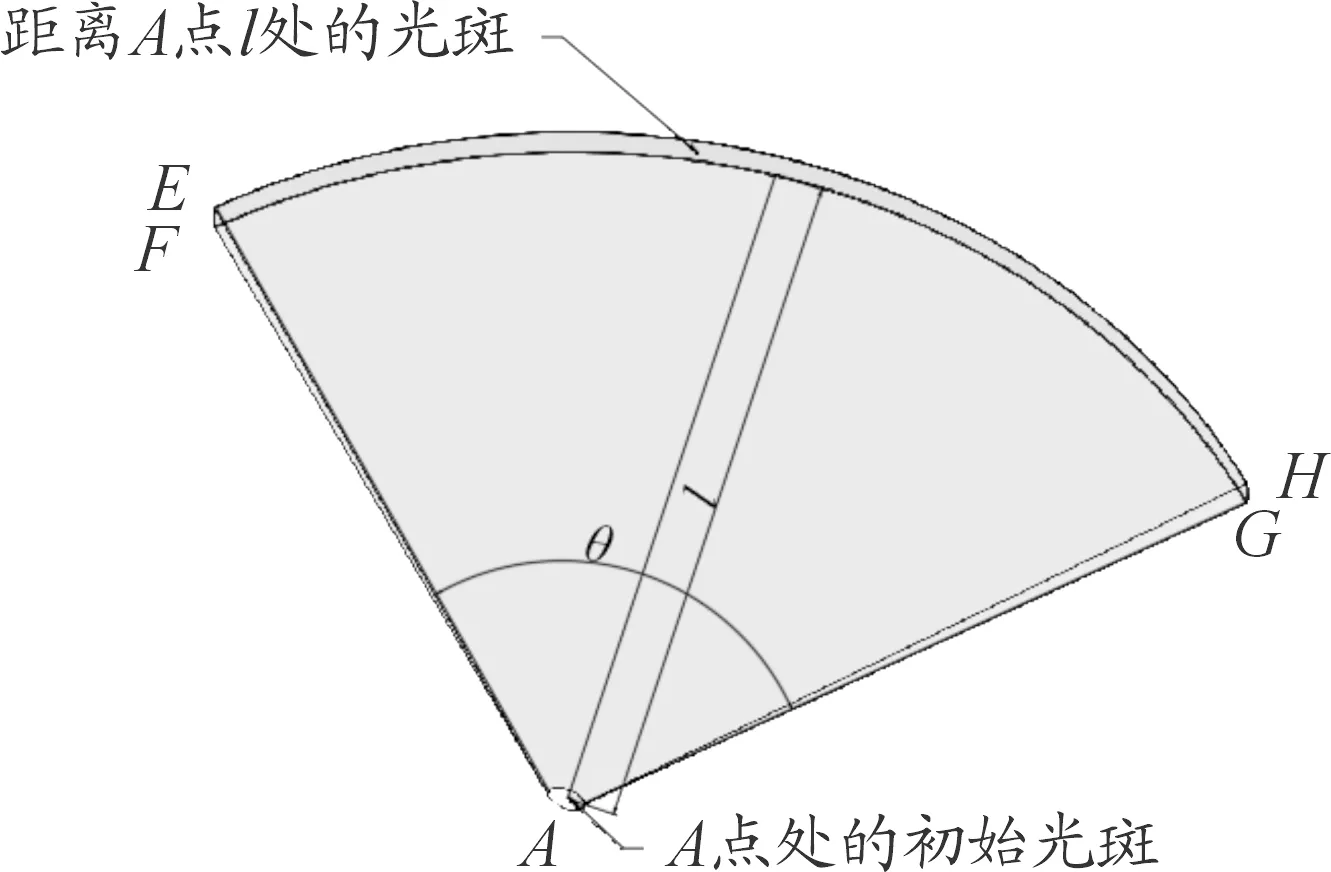
圖2 點光斑擴展為線光斑的示意圖

圖3 柱面鏡到原向反射膜的光路示意圖

(4)
(5)
當彈丸穿過光幕的瞬間會遮擋住部分由A點入射到原向反射膜上的光線,即原向反射膜上從n1到n2段無法接收到入射光線,如圖4所示;同時對于從n3到n1段和從n2到n4段,雖然可以接收到由A點入射的光線,但這兩段反射出的光線會有部分被彈丸遮擋住,因而不能被菲涅爾透鏡接收到,如圖5所示。

圖4 遮擋的入射光通量示意圖
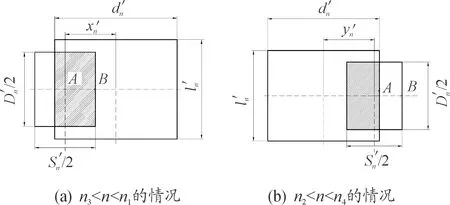
(xn1,yn1),(xn2,yn2),(xn3,yn3),(xn4,yn4)分別為n1、n2、n3、n4的坐標,則對于彈丸坐標x′ yn1=yn2=yn3=yn4=l1 (6) (7) (8) (9) 式中:De為彈丸直徑;l1為上方原向反射膜的長度;αn為入射角;βn為逆反射發散角。 圖5 遮擋的逆反射光通量示意圖 對于n1到n2段上的任意一小分段,如圖6所示,反射回A點處的總光斑可以近似看作矩形區域,其面積記為A3,菲涅爾透鏡能接收到的反射光斑區域的面積記為A4,將A4與A3的比值記為μ1(稱為菲涅爾透鏡的接收率),則: (10) (11) (12) (13) (14) 其他情況的分析方法與該情況類似,在此由于篇幅原因省略。 圖6 反射光線可接收光斑面積示意圖 (15) (16) 對于從n3到n1段與n2到n4段上的任意一小分段,如圖7所示,A5為該段原向反射膜反射回菲涅爾透鏡表面上的光斑面積,將A5與A3的比值記為μ2(稱為彈丸對反射光線的遮擋率)。則: (17) 當n3 (18) (19) 當n2 (20) (21) 圖7 彈丸遮擋反射光線光斑面積示意圖 (22) (23) 則彈丸穿過光幕時遮擋的總光通量為ΔΦ: (24) 對于靶面為10 m×10 m的探測幕面,則原向反射膜的長l1=10 m,取m=20 000,將每段分為1 mm,A點處一字線光源的光通量為ΦA=200 mW,一字線光源的初始直徑為d=4.5 mm,柱面鏡擴束后發散角θ=90°,使用的原向反射膜的逆反射發散角為γ≈1.03,原向反射膜的逆反射率與入射角αn有如下關系: (25) 1) 當彈丸口徑d′=5.8 mm,彈丸長度為l′=50 mm,而過幕位置坐標(x′,y′)改變時,對其遮擋光通量ΔΦ模型進行仿真,如圖8所示;由圖8的仿真可知:仿真圖示是關于x′=y′對稱的,隨著彈丸過幕坐標x′與y′逐漸增大,遮擋光通量ΔΦ逐漸減小;隨著入射角αn逐漸增大,遮擋光通量ΔΦ逐漸減小。 2) 當彈丸過幕位置坐標(x′,y′)不發生變化,而彈丸直徑d′改變時,對其遮擋光通量ΔΦ模型進行仿真,如圖9所示;由圖9的仿真可知隨著彈丸直徑d′逐漸增大,遮擋光通量ΔΦ逐漸增大。 圖8 d′=5.8 mm, l′=50 mm彈丸在探測幕面不同位置的探測性能仿真結果 圖9 彈丸過幕位置相同,彈丸直徑不同的靈敏度仿真結果 為了驗證上述的仿真結果,進行實驗驗證。由式(24)可知:在其他參數不變的情況下,當激光器功率增大(即ΦA增大),遮擋的總光通量為ΔΦ隨之增大;靈敏度分布是關于x′=y′對稱的。 由于條件限制,將激光器的功率調節為仿真時的四分之一,構建了一個4 m×4 m的靶面,如圖10所示為系統實驗裝置示意圖。 圖10 系統實驗裝置示意圖 實驗時,使用波長為650 nm、輸出功率為50 mW、光源初始直徑為4.5 mm、出光張角為90°的可見紅光一字線激光器,型號為C000398 3M-2的長度為8 m的原向反射膜,焦距為50 mm、通光口徑為100 mm的菲涅爾透鏡和條形硅光電二級管等器件;將原向反射膜先從左向右再從上向下分成8 000段,激光器主點到菲涅爾透鏡中心距離為60 mm,使用彈丸直徑6 mm的氣槍彈進行實驗,在入射角αn為0°、20°、45°三種情況下,對彈丸過幕的x′坐標為0.5~3.5 m之間每隔0.5 m打一槍,使用示波器觀測并記錄系統輸出的波形。 當入射角αn為0°時,實驗數據如表1所示。 當入射角αn為20°時,實驗數據如表2所示。 當入射角αn為45°時,實驗數據如表3所示。 分析實驗數據可以得到:當坐標x′不變時,隨著入射角αn逐漸增大,輸出幅值V逐漸減小;當入射角αn不變時,隨著坐標x′逐漸增大,輸出幅值V逐漸減小。實驗與仿真的靈敏度變化規律一致。坐標y′的情況與上述結果類似,不在進行重復進行實驗。在此條件下,對于直徑為6 mm及其以上的氣槍彈,其穿過4 m×4 m的整個靶面時均可以被探測到,則提出的探測系統可以滿足大靶面光幕探測要求。 表1 入射角αn=0°時實驗數據 表2 入射角αn=20°時實驗數據 表3 入射角αn=45°時實驗數據 通過對原向反射式探測光幕的原理分析,推導了其靈敏度模型,并對靈敏度模型進行了仿真與驗證。研究分析表明:理論推導得到的本系統靶面內的靈敏度變化趨勢與實彈實驗測得的靈敏度變化趨勢一致;當彈丸直徑不變時,隨著彈丸過幕坐標(x′,y′)逐漸增大,探測靈敏度逐漸減小;隨著入射角αn逐漸增大,探測靈敏度逐漸減小。當彈丸過幕位置坐標(x′,y′)不變時,隨著彈丸直徑d′逐漸增大,探測靈敏度逐漸增大。在設定的系統參數下進行實驗,對于直徑6 mm及其以上的氣槍彈,其穿過3.5 m×3.5 m的整個靶面時均可以被有效探測到。因此,將激光功率按比例提高后(考慮到大氣衰減,可略微大一些),所實現的探測系統即可滿足大靶面光幕探測要求。


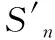




3 探測性能仿真



4 驗證




5 結論

