捷聯(lián)星光復(fù)合制導(dǎo)修正方法研究

張 青,王勝永,傅 瑜,王 勇,林海奇

(北京宇航系統(tǒng)工程研究所， 北京 100076)

在航天技術(shù)不斷發(fā)展的今天，現(xiàn)代飛行器對(duì)導(dǎo)航精度要求越來(lái)越高。若單純依靠慣性制導(dǎo)系統(tǒng)提高導(dǎo)航精度，將帶來(lái)極大的技術(shù)難度和成本的急劇增加[1]。慣性星光復(fù)合制導(dǎo)是解決此問題的有效途徑。相比于平臺(tái)星光復(fù)合制導(dǎo)，捷聯(lián)星光復(fù)合制導(dǎo)具有體積小、重量輕、成本低、可靠性高、便于維護(hù)等優(yōu)點(diǎn)，已經(jīng)成為高性能導(dǎo)航的重要發(fā)展方向。

目前，國(guó)內(nèi)已經(jīng)有一些機(jī)構(gòu)對(duì)捷聯(lián)星光制導(dǎo)系統(tǒng)展開了研究。文獻(xiàn)[2]提出了基于慣性星光測(cè)量信息的飛行器關(guān)機(jī)點(diǎn)速度位置誤差分離方法；文獻(xiàn)[3]和文獻(xiàn)[4]介紹了星光修正原理，并提出了基于卡爾曼濾波的星光修正方法；文獻(xiàn)[5]對(duì)捷聯(lián)星光復(fù)合制導(dǎo)方案的即時(shí)修正效果進(jìn)行了分析；文獻(xiàn)[6]研究了星光測(cè)量信息修正捷聯(lián)慣性導(dǎo)航初始對(duì)準(zhǔn)誤差的方法；文獻(xiàn)[7]提出了捷聯(lián)星光制導(dǎo)仿真的方法與流程；文件[8] 對(duì)捷聯(lián)星光雙星修正方案對(duì)制導(dǎo)精度和星光觀測(cè)信息的影響情況進(jìn)行了數(shù)學(xué)仿真；文獻(xiàn)[9]對(duì)比分析了雙星修正和單星修正兩種方案的特點(diǎn)。

雖然許多研究人員已經(jīng)對(duì)捷聯(lián)星光修正方法進(jìn)行了大量研究，并提出了多種修正方法，但是各種方法在工程上的適用對(duì)象和使用條件均未明確，部分情況存在較大局限性。本文建立了星光測(cè)量模型、慣性系統(tǒng)誤差模型和星光修正模型，提出了兩種工程上實(shí)際可用的捷聯(lián)星光修正方法，并通過仿真算例研究了兩種方法的適用情況。

1 坐標(biāo)系定義

1) 發(fā)射慣性坐標(biāo)系OXIYIZI。坐標(biāo)系原點(diǎn)O位于發(fā)射點(diǎn)；OXI軸在發(fā)射點(diǎn)水平面內(nèi)，指向發(fā)射瞄準(zhǔn)方向；OYI軸與垂直于發(fā)射點(diǎn)水平面，方向向上；OZI軸在當(dāng)?shù)厮矫鎯?nèi)，三軸構(gòu)成右手正交坐標(biāo)系。發(fā)射后坐標(biāo)系不隨地球轉(zhuǎn)動(dòng)，成為慣性坐標(biāo)系。星光矢量在發(fā)射慣性系中的表示如圖1所示。

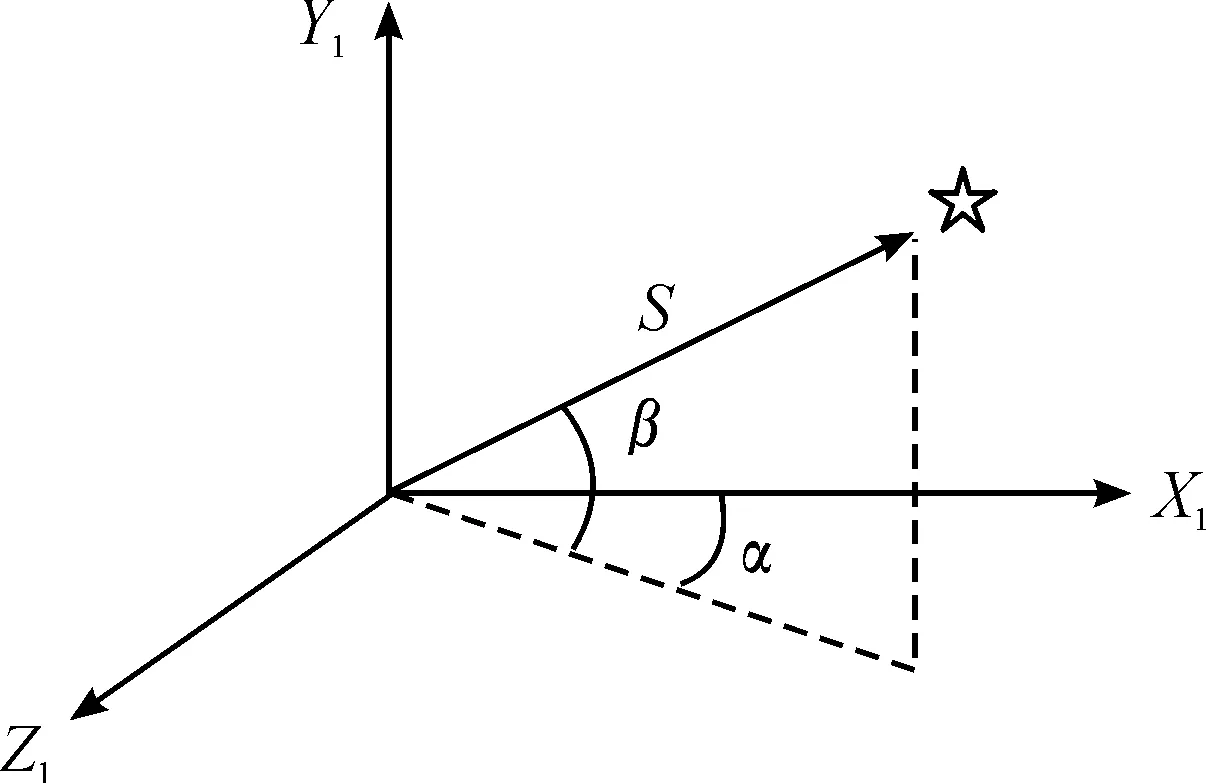
圖1 星光矢量在發(fā)射慣性坐標(biāo)系中的表示

2) 飛行器坐標(biāo)系OXbYbZb。坐標(biāo)系原點(diǎn)O位于飛行器質(zhì)心；OXB軸沿飛行器的縱軸指向頭部方向；OYB軸在飛行器的縱平面內(nèi)與OXB軸垂直且指向上方；OZB軸與OXB、OYB軸構(gòu)成右手正交坐標(biāo)系。飛行器在發(fā)射慣性坐標(biāo)系中的角位置由俯仰角φa、偏航角ψa和滾動(dòng)角γa確定。則發(fā)射慣性坐標(biāo)系到飛行器坐標(biāo)的轉(zhuǎn)換矩陣可以表示為

(1)

3) 導(dǎo)航坐標(biāo)系OXnYnZn。捷聯(lián)慣導(dǎo)系統(tǒng)在求解導(dǎo)航參數(shù)時(shí)所采用的坐標(biāo)系，即數(shù)學(xué)平臺(tái)，在沒有誤差的情況下，坐標(biāo)軸方向與發(fā)射慣性系一致。

4) 星敏感器坐標(biāo)系OXSYSZS。星敏感器坐標(biāo)系原點(diǎn)O位于光學(xué)鏡頭的焦平面(CCD)中心；OXS軸與光學(xué)鏡頭軸線一致；YSOZS平面與CCD所在平面一致，OYS軸為CCD像元垂直讀出方向，OZS軸為CCD像元水平讀出方向。它與飛行器坐標(biāo)系之間的轉(zhuǎn)換關(guān)系在星敏感器安裝時(shí)即已確定。星光矢量在星敏感器坐標(biāo)系中的表示見圖2。

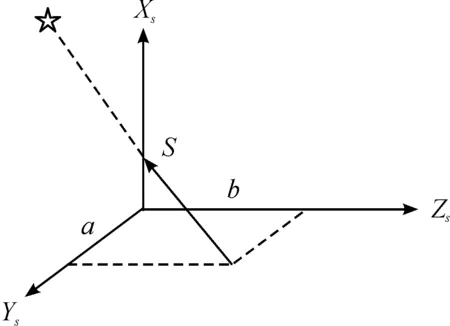
圖2 星光矢量在星敏感器坐標(biāo)系中的表示

2 捷聯(lián)星光測(cè)量模型

捷聯(lián)星光復(fù)合制導(dǎo)系統(tǒng)是將星敏感器和捷聯(lián)慣組固連安裝在飛行器上，通過對(duì)預(yù)先設(shè)定的兩顆及以上恒星進(jìn)行測(cè)量，估計(jì)導(dǎo)航坐標(biāo)系相對(duì)理論發(fā)射慣性坐標(biāo)系的漂移角，并以此來(lái)修正慣性器件的基準(zhǔn)誤差引起的落點(diǎn)偏差，其相應(yīng)的制導(dǎo)方案原理如圖3所示。

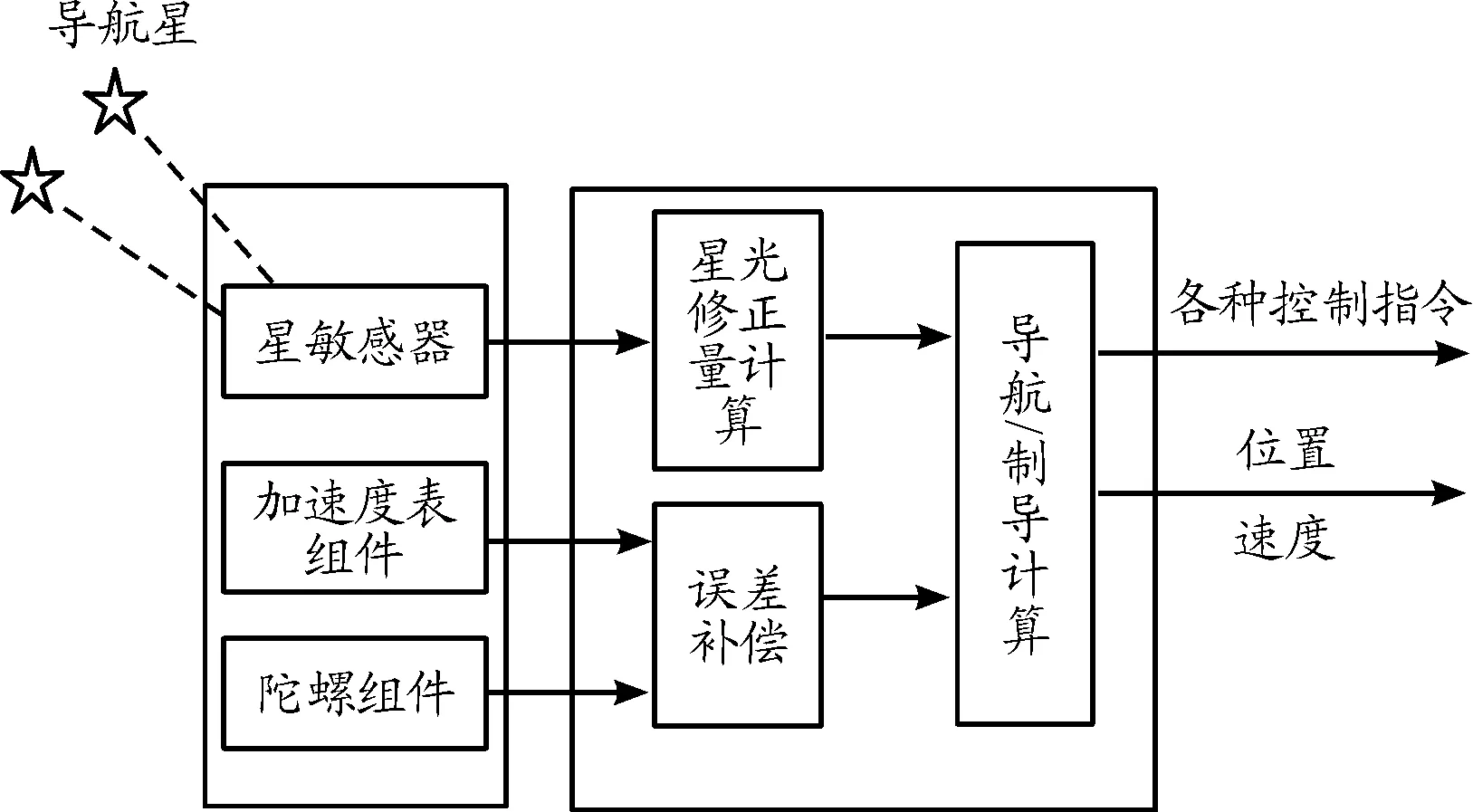
圖3 捷聯(lián)/星光復(fù)合制導(dǎo)方案示意圖

(2)

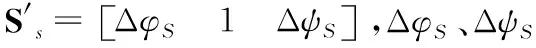
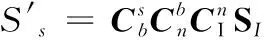
(3)

由式(2)和式(3)可以推導(dǎo)得到，星敏感器測(cè)量輸出量ΔφS、ΔψS與姿態(tài)誤差αx、αy、αz的關(guān)系，即：

(4)

飛行器對(duì)空間內(nèi)兩顆恒星進(jìn)行測(cè)量時(shí)，可以得到：

(5)

式中，ΔφS1、ΔψS1和ΔφS2，ΔψS2分別為兩顆恒星的星敏感器測(cè)量輸出；φa1、ψa1、γa1為測(cè)量第一顆導(dǎo)航星時(shí)的飛行器姿態(tài)角；φa2、ψa2、γa2為測(cè)量第二顆導(dǎo)航星時(shí)的飛行器姿態(tài)角。

根據(jù)式(5)，可以由兩顆導(dǎo)航星星光測(cè)量輸出量求解得到導(dǎo)航坐標(biāo)系到發(fā)射慣性坐標(biāo)系的姿態(tài)誤差αx、αy、αz(簡(jiǎn)稱數(shù)學(xué)平臺(tái)漂移角)，進(jìn)而利用星光修正方法能夠?qū)υ撜`差進(jìn)行修正。因此，捷聯(lián)星光修正能夠?qū)λ幸饠?shù)學(xué)平臺(tái)漂移角的誤差進(jìn)行修正，對(duì)無(wú)法引起數(shù)學(xué)平臺(tái)漂移角的誤差不能進(jìn)行修正。

3 捷聯(lián)星光工具誤差模型

3.1 陀螺儀誤差模型

陀螺儀誤差模型如下：

δωx1=D0x+K1bx·ωx1

δωy1=D0y+K1by·ωy1

δωz1=D0z+K1bz·ωz1

(6)

式中，ωx1、ωy1、ωz1為飛行器角速度在飛行器坐標(biāo)系內(nèi)的投影；δωx1、δωy1、δωz1為飛行器角速度誤差在飛行器坐標(biāo)系內(nèi)的投影；D0x、D0y、D0z為陀螺儀與角速度無(wú)關(guān)的誤差系數(shù)；K1bx、K1by、K1bz為陀螺儀與角速度一次方成比例的誤差系數(shù)。

飛行器姿態(tài)角變化率誤差與飛行器角速度誤差關(guān)系[10]如下：

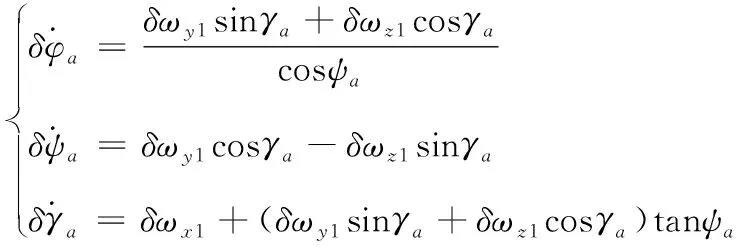
(7)

通過對(duì)式(7)積分可以得到姿態(tài)角誤差Δφa、Δψa、Δγa，進(jìn)而得到導(dǎo)航坐標(biāo)系到發(fā)射慣性坐標(biāo)系的姿態(tài)誤差αqx、αqy、αqz，即：

(8)

因此，陀螺儀誤差將引起數(shù)學(xué)平臺(tái)漂移角，能夠通過星光測(cè)量進(jìn)行修正。

3.2 加速度計(jì)誤差模型

加速度計(jì)誤差模型如下：

(9)

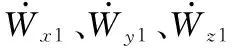
可以看到加速度計(jì)誤差不會(huì)引起數(shù)學(xué)平臺(tái)漂移角，因此星光修正無(wú)法對(duì)加速度計(jì)誤差進(jìn)行修正。

3.3 初始對(duì)準(zhǔn)誤差模型

初始對(duì)準(zhǔn)誤差將直接導(dǎo)致導(dǎo)航坐標(biāo)系相對(duì)發(fā)射慣性坐標(biāo)系存在角度偏差，因此星光修正能夠?qū)Τ跏紝?duì)準(zhǔn)誤差進(jìn)行修正，其誤差模型如下：

(10)

式中，kp0x、kp0y、kp0z為三方向初始對(duì)準(zhǔn)誤差。

4 捷聯(lián)星光修正模型

采用星光復(fù)合制導(dǎo)方案時(shí)，通過測(cè)量2顆恒星，利用式(5)可以解算得到由各項(xiàng)誤差引起的數(shù)學(xué)平臺(tái)漂移角。對(duì)該漂移角引起的偏差進(jìn)行修正，則可提高飛行器導(dǎo)航精度。

相同的數(shù)學(xué)平臺(tái)漂移角下，不同星光修正方法得到的星光修正效果不同，對(duì)應(yīng)的飛行器導(dǎo)航偏差也不同。下面針對(duì)修正系數(shù)法和直接補(bǔ)償法2種星光修正方法進(jìn)行詳細(xì)介紹。

4.1 修正系數(shù)法

修正系數(shù)法是利用飛行前計(jì)算得到的星光修正系數(shù)和飛行過程中測(cè)量得到的星光測(cè)量輸出值，計(jì)算由數(shù)學(xué)平臺(tái)漂移角引起的導(dǎo)航偏差，即星光修正量，可以表示為

(11)

式中，ΔLs、ΔHs為縱橫向星光修正量；u1αx、u1αy、u1αz、u2αx、u2αy、u2αz為星光修正系數(shù)；αx、αy、αz為利用星光測(cè)量量解算得到的數(shù)學(xué)平臺(tái)漂移角。

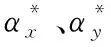
(12)

式中，δL、δH為飛行器綜合縱橫向落點(diǎn)偏差；ΔL、ΔH為由捷聯(lián)慣性系統(tǒng)引起的縱橫向偏差偏差[12]。

4.2 直接補(bǔ)償法

捷聯(lián)星光復(fù)合制導(dǎo)方案下，除了修正系數(shù)法外，還可以利用直接補(bǔ)償法進(jìn)行星光修正。通過星光測(cè)量輸出值解算得到數(shù)學(xué)平臺(tái)漂移角，對(duì)引起數(shù)學(xué)平臺(tái)漂移角的誤差項(xiàng)進(jìn)行權(quán)重配置，并基于該權(quán)重及相關(guān)誤差模型，采用飛行器真實(shí)軌跡參數(shù)計(jì)算得到由數(shù)學(xué)平臺(tái)漂移角引起的視速度誤差δW和視位置差δS，然后利用式(13)對(duì)飛行速度導(dǎo)航參數(shù)、位置導(dǎo)航參數(shù)進(jìn)行直接補(bǔ)償。

(13)

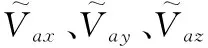
對(duì)于動(dòng)基座發(fā)射的飛行器，初始對(duì)準(zhǔn)誤差較大，采用直接補(bǔ)償法進(jìn)行星光修正時(shí)，一般將數(shù)學(xué)平臺(tái)漂移角當(dāng)作初始對(duì)準(zhǔn)誤差進(jìn)行視速度誤差、視位置誤差進(jìn)行計(jì)算，即：

(14)

直接補(bǔ)償法下，星光修正量計(jì)算方法如下式所示：

(15)

4.3 捷聯(lián)星光修正流程圖

捷聯(lián)星光修正流程框圖見圖4。可以看到，無(wú)論采用哪種方法進(jìn)行捷聯(lián)星光修正，都需要提前預(yù)估飛行軌跡，并選取導(dǎo)航星。采用修正系數(shù)法進(jìn)行修正時(shí)，還需要基于地面試驗(yàn)獲取各項(xiàng)誤差的估計(jì)值，計(jì)算星光修正系數(shù)，測(cè)星后計(jì)算星光修正量，對(duì)目標(biāo)點(diǎn)偏差進(jìn)行修正，減小飛行偏差；采用直接補(bǔ)償法進(jìn)行修正時(shí)，測(cè)星后利用實(shí)際飛行軌跡計(jì)算速度偏差、位置偏差，直接對(duì)飛行導(dǎo)航參數(shù)進(jìn)行修正，減小飛行偏差。

因此，從方法上來(lái)看，修正系數(shù)法更加依賴于飛行前的信息，而直接補(bǔ)償法要求準(zhǔn)確解算數(shù)學(xué)平臺(tái)漂移角引起的速度偏差和位置偏差。

圖4 捷聯(lián)星光修正流程框圖

5 仿真算例

由3.2可知，采用星光復(fù)合制導(dǎo)方案無(wú)法對(duì)加速度計(jì)誤差進(jìn)行修正。因此，為了更加清楚說(shuō)明不同星光修正方法的效果，本節(jié)在設(shè)計(jì)仿真算例時(shí)，僅考慮可以進(jìn)行修正的陀螺儀誤差和初始對(duì)準(zhǔn)誤差。表1中給出了5種仿真條件(仿真變量具體含義見第3節(jié)內(nèi)容)，分別說(shuō)明陀螺儀誤差、初始對(duì)準(zhǔn)誤差及其估計(jì)值的準(zhǔn)確度(通過地面試驗(yàn)獲得誤差估計(jì)值，其與誤差實(shí)際值一般存在差異，差異的大小與地面試驗(yàn)的方法、周期等相關(guān))對(duì)2種方法星光修正效果的影響。

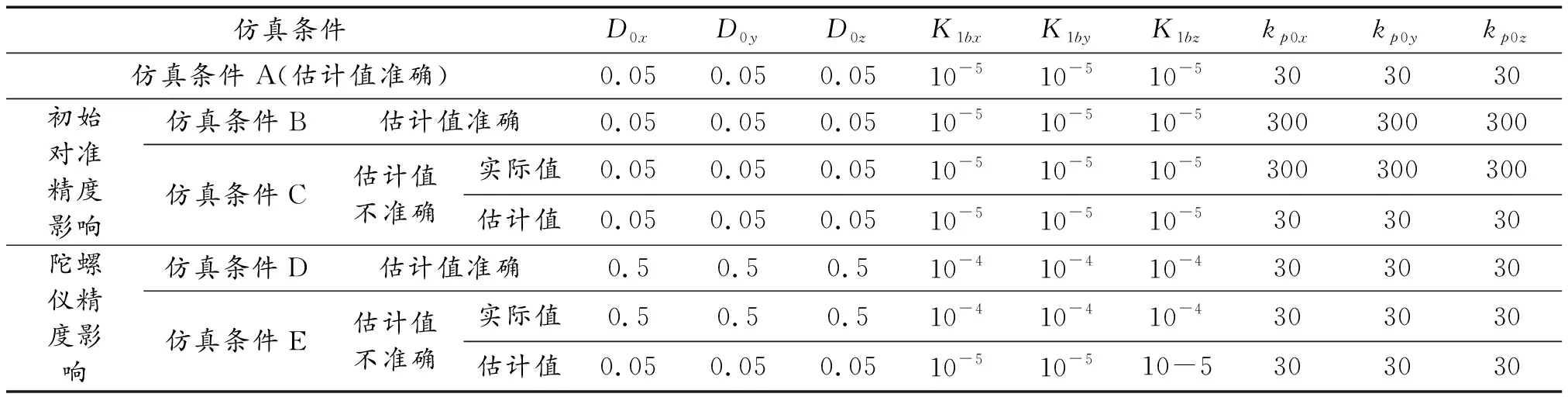
表1 仿真條件

依據(jù)表1中的仿真條件，對(duì)2種星光修正方法的落點(diǎn)偏差進(jìn)行仿真計(jì)算，結(jié)果見表2。

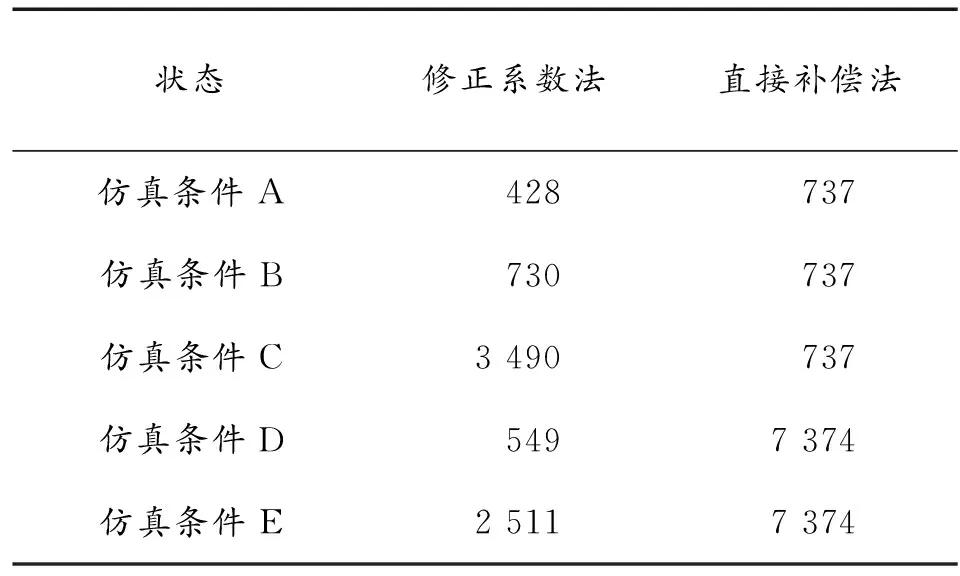
表2 落點(diǎn)偏差的仿真計(jì)算結(jié)果 m

通過分析仿真結(jié)果可以看到：

1) 分別對(duì)比算例B和算例C、算例D和算例E，可以看到無(wú)論是陀螺儀誤差還是初始對(duì)準(zhǔn)誤差，誤差的估計(jì)值與實(shí)際值存在差異時(shí)，采用修正系數(shù)法進(jìn)行星光修正，修正效果降低，落點(diǎn)偏差增大；采用直接補(bǔ)償法進(jìn)行星光修正，修正效果不受影響；為了進(jìn)一步說(shuō)明該結(jié)論，開展了2種方法落點(diǎn)偏差隨初始對(duì)準(zhǔn)誤差準(zhǔn)確度變化的仿真分析，結(jié)果見圖5。

2) 分別對(duì)比算例A和算例B、算例A和算例D，可以看到當(dāng)誤差估計(jì)值與實(shí)際值一致時(shí)，采用修正系數(shù)法進(jìn)行星光修正，陀螺儀誤差變化和初始對(duì)準(zhǔn)誤差變化對(duì)星光修正效果影響均較小；采用直接補(bǔ)償法進(jìn)行星光修正，初始對(duì)準(zhǔn)誤差變化對(duì)星光修正無(wú)影響，但陀螺儀誤差變化對(duì)星光修正影響較大；為了進(jìn)一步說(shuō)明該結(jié)論，開展了2種方法落點(diǎn)偏差隨陀螺儀誤差值變化的仿真分析，結(jié)果見圖6。

3) 對(duì)比算例A和算例E，可以看到陀螺儀誤差實(shí)際值相對(duì)于估計(jì)值變差時(shí)，采用修正系數(shù)法和直接補(bǔ)償法進(jìn)行星光修正，修正效果都會(huì)降低，但直接補(bǔ)償法下導(dǎo)航精度降低更多；為了進(jìn)一步說(shuō)明該結(jié)論，開展了2種方法落點(diǎn)偏差隨陀螺儀誤差值及估計(jì)值值準(zhǔn)確度變化的仿真分析，結(jié)果見圖7。

圖5 初始對(duì)準(zhǔn)誤差估計(jì)值準(zhǔn)確度對(duì)落點(diǎn)偏差的影響曲線

圖6 陀螺儀誤差變化對(duì)落點(diǎn)偏差的影響曲線

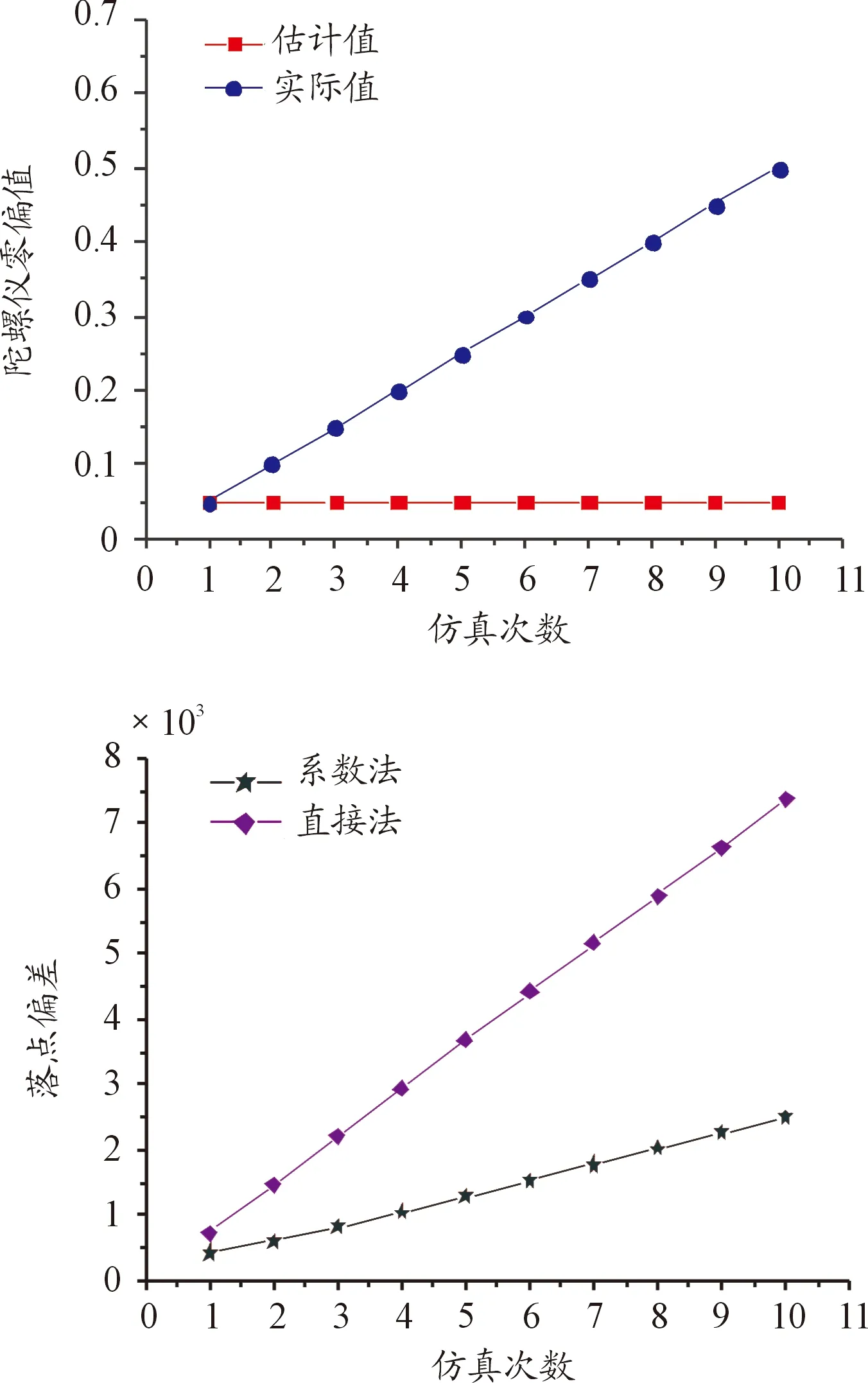
圖7 陀螺儀誤差值及準(zhǔn)確度對(duì)落點(diǎn)偏差的影響曲線

6 結(jié)論

本文重點(diǎn)對(duì)捷聯(lián)星光復(fù)合制導(dǎo)方案2種修正方法——修正系數(shù)法和直接補(bǔ)償法，進(jìn)行了建模與算例仿真分析，可以看到儀表誤差特性不同，2種修正方法的應(yīng)用效果不同。其主要原因在于：

1) 修正系數(shù)法需要基于儀表誤差估計(jì)值計(jì)算修正系數(shù)，該系數(shù)與儀表誤差估計(jì)值相匹配，當(dāng)儀表誤差實(shí)際表現(xiàn)值與地面估計(jì)值一致時(shí)，星光修正效果好，當(dāng)儀表誤差實(shí)際表現(xiàn)值與地面估計(jì)值存在較大差異時(shí)，修正系數(shù)與儀表誤差的實(shí)際值不再匹配，導(dǎo)致修正系數(shù)法修正效果降低；

2) 直接補(bǔ)償法是在飛行器飛行過程中，通過觀星直接解算得到數(shù)學(xué)平臺(tái)漂移角，與儀表誤差的地面估計(jì)值無(wú)關(guān)，因此地面估計(jì)值的準(zhǔn)確度不影響直接補(bǔ)償法的星光修正效果；但是由于無(wú)法區(qū)分陀螺儀誤差和初始對(duì)準(zhǔn)誤差引起數(shù)學(xué)平臺(tái)漂移角的比例，一般按照初始對(duì)準(zhǔn)誤差對(duì)漂移角修正，當(dāng)陀螺儀誤差實(shí)際值較大時(shí)，直接補(bǔ)償法星光修正效果大幅降低。

通過本文分析，可以提出2種星光修正方法的適用條件：儀表誤差地面估計(jì)值與實(shí)際表現(xiàn)值一致性較好時(shí)，應(yīng)采用修正系數(shù)法進(jìn)行星光修正；初始對(duì)準(zhǔn)誤差地面估計(jì)值與實(shí)際表現(xiàn)值差異較大時(shí)，應(yīng)采用直接補(bǔ)償法進(jìn)行星光修正；陀螺儀誤差地面估計(jì)值與實(shí)際表現(xiàn)值差異較大時(shí)，2種方法修正效果均降低，應(yīng)考慮提升陀螺儀精度或改善地面試驗(yàn)方法。