路面激勵對火箭炮行進間發射控制的影響研究

孫志群，李 強，袁 衛，曾正森，李世康

(1.中北大學 機電工程學院， 太原 030051； 2.重慶長安工業有限責任公司, 重慶 400000)

火箭炮是一種大面積殺傷武器，配合制導彈藥，已經使行進間發射成為可能，提高行進間發生調炮精度成為重中之重。車載火箭炮的行進間發射大大提高了武器系統的作戰效能，但在武器系統行進時，車體隨著路面的起伏而振動，嚴重影響火箭炮的射擊精度。行進間發射涉及地面力學、車輛動力學及發射動力學[1]，其各個學科的耦合對于火箭炮的調炮控制提出了更高的要求。目前對于調炮控制的研究較多，但主要側重于控制方法的研究，文獻[2-3]應用滑模控制和PID控制方式對火箭炮固定發射調炮控制進行研究，未考慮實際系統的動力學模型。事實上，火箭炮發射過程中，受到沖擊載荷后整個系統發生振動，對于作動器的干擾不能忽略，行進間發射路面顛簸形成的干擾會對控制精度產生影響，隨著防空武器精度要求的提高，這一差異逐漸凸顯，不容忽視。

由于火箭炮行進間發射要求較高，目前對于火箭炮行進間發射的研究較少，但坦克行進間發射已有眾多研究。金濤等[4]通過建立坦克多剛體模型，采用 PID(proportion integration differentiation) 控制對坦克火炮進行控制，說明了在坦克高速行駛時，PID控制依然能較好控制火炮。史力晨、陳宇等[5-6]通過狀態方程法建立了坦克、火炮系統的振動模型，將系統的動力學響應看作了多剛體系統對地面不平度激勵的響應問題，穩定器作用通過剛性系數體現，計算分析了坦克行進間火炮運動規律;但車載火箭炮系統重量較坦克輕，采用輪胎行進的方式對路面狀況更為敏感，須對其行進間發射控制性能單獨研究。

本文擬采用機電耦合方法研究火箭炮行進間發射中，路面不平度對于PID控制的影響，首先利用Adams基于拉格朗日方程建立車載火箭炮系統的動力學模型，并利用諧波疊加法建立三種代表性路面不平度，最后通過Matlab/Simulink建立大功率伺服電機控制模型，聯合仿真計算火箭炮行進間發射PID控制的有效性，并給出路面不平度對控制精度的影響。

1 車載火箭炮系統動力學模型

本文模型為6×6輪式底盤、箱式多管火箭炮系統。動力學模型分為兩部分：運載車體和火箭炮發射系統。車體包括車輪、懸架、車架；發射部分包括高低機、方向機及發射箱。

1.1 車體部分建模

車體動力學模型在Adams/View環境下構建。輪胎是車輛至關重要的部分，起到驅動車體行進、支撐車體、抑制路面不平度引起的振動與沖擊的作用。因此，輪胎模型對整體仿真產生很大影響，Adams中提供了多種輪胎模型用于不同車輛的仿真計算。本文計算內容主要考慮車體直線運動時車體振動，不涉及車輛平順性及耐久性分析，因此選擇采用UA輪胎模型。設置輪胎半徑0.75 m；輪胎斷面寬度0.40 m；徑向剛度870 N/mm；徑向阻尼80 N·s/mm。設置輪胎6輪驅動，直線行駛速度50 km/h。

車體懸架與車體連接位置、方式及自身尺寸參數影響車輛振動特性，所以采用原車懸架設計尺寸及連接方式，減震器用彈簧代替，設置彈簧剛度1 000 N/mm，阻尼112 N·s/mm。懸架具體結構如圖1所示。

圖1 車輛懸架

1.2 發射部分動力學模型

發射部分底座與車體做固定鉸連接；方向機與底座設置旋轉鉸連接；發射箱繞高低機軸旋轉；左右發射箱各20發火箭彈，且火箭彈與定向器碰撞接觸。

接觸碰撞通常采用非線性彈簧-阻尼模型進行計算，兩物體發生碰撞的判斷條件為是否產生穿透，當穿透量小于零時，兩物體間的碰撞力零，否則碰撞力正。碰撞力的定義[7]如下：

(1)

式中：k為碰撞表面的剛度；e為彈性系數；δi為穿透力量；cmax為最大阻尼系數；δmax為最大穿透量。可由以Hertz定律為理論基礎的剛度計算公式給出。

在確定的控制方式下，火箭炮行進間發射調炮精度主要受路面激勵及火箭彈燃氣流沖擊的影響，對這兩部分載荷的施加至關重要。關于路面激勵的施加，將在后面章節給出。通過實驗得到火箭彈燃氣射流對定向管X、Y、Z方向的沖擊力，其力值隨時間變化情況如圖2所示。

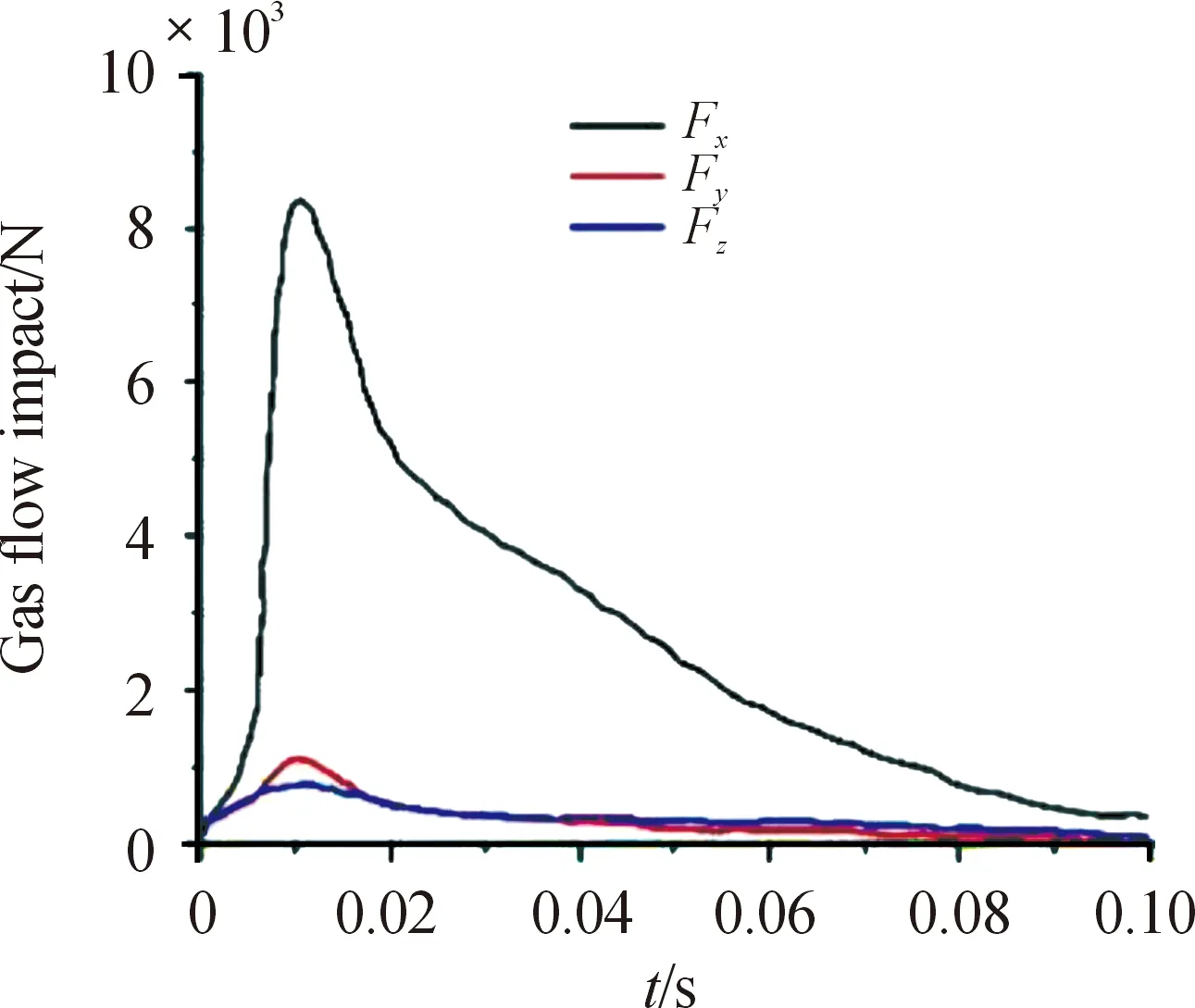
圖2 火箭彈燃氣流沖擊力曲線

2 路面譜建立

2.1 諧波疊加原理

國際標準化組織(ISO)和我國國標GB/T7031—2005均采用下式功率譜密度函數擬合[8]：

(2)

式中：n為空間頻率；為波長λ的倒數，表示每米長度中包括幾個波長；n0為參考空間頻率n0=m-1;Gq(n0)為路面不平度系數，它是參考頻率n0下的路面功率譜密度；W為頻率指數-雙對數坐標上的斜線斜率，決定著路面功率譜密度的頻率結構，一般取2。

按照Gq(n0)的不同可以將路面分為A～H 8個等級(表1)，值越大，表明路面不平度越大，對車輛振動影響越大。

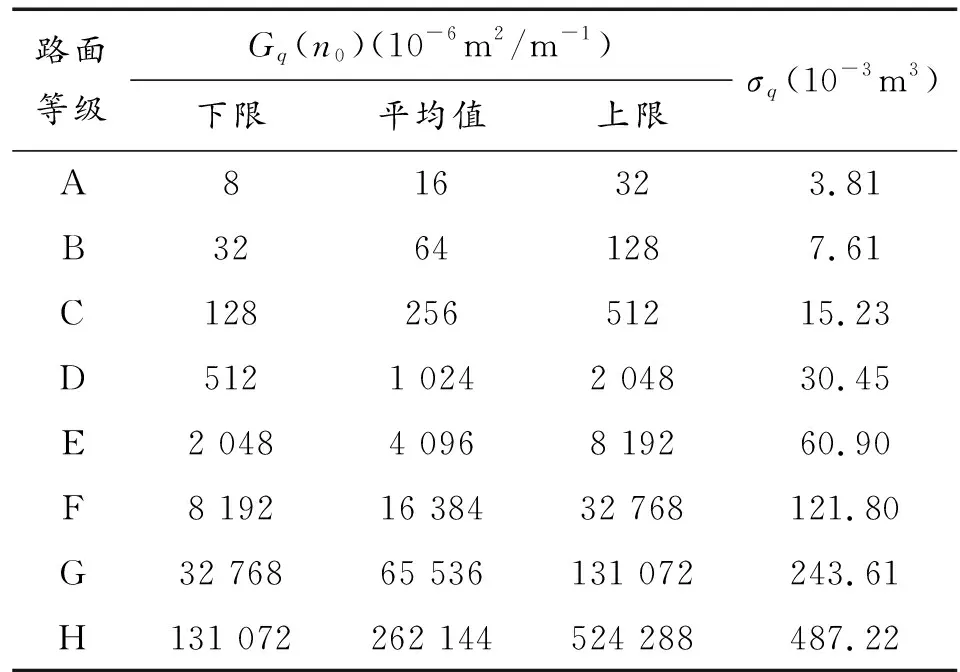
表1 路面不平度參數

式(2)是基于空間頻率的表達式，由車速和時間頻率之間的關系可以寫出時域下的表達式[9]：

f=vn

(3)

(4)

其中：f為時間頻率(Hz);v為車速(m/s)。路面不平度的方差可以表示為：

(5)

將f劃分為N個小區間，用每個區間的中心頻率fi處的譜密度值Gq(fi)代替Gq(f)在小區間內的值，則：

(6)

其中：δf=(fl-fu)/N。則每個小區間的路面不平度幅值：

(7)

那么用標準差為Ai的正弦波函數表示每個區間的路面模型為：

(8)

其中θi為區間[0,2π]內的隨機數。最后將小區間的正弦波疊加在一起，得到時域內隨機路面不平度模型：

(9)

轉換為空間域內的表達式為：

(10)

由于汽車振動系統的固有頻率在0.7～15 Hz，常用車速為36～180 km/h(10～50 m/s)[10],取地面作用于輪胎的激勵時間頻率下限為fl=0.5 Hz、上限為fu=30 Hz則研究車輛振動時需要的空間頻率上、下限分別為：

(11)

(12)

由式(11)(12)可知，在0.01～3 m-1的空間頻率內模擬路面不平度，便可覆蓋車輛系統的固有頻率，從而保證由諧波疊加法所得的路面不平度作為激勵，車輛振動情況結論符合實際情況。

由奈奎斯特采樣定理：采樣頻率ns≥2nu，采樣間隔Δx、Δy必須滿足

由此Δx≤0.166 7 m, Δy≤0.166 7 m,本文取Δx=0.1 m。

2.2 路面譜實現及應用

基于諧波疊加法編寫Matlab算法，生成A級、D級、F級3種路面不平度路面，其三維路面譜如圖3～圖5所示。

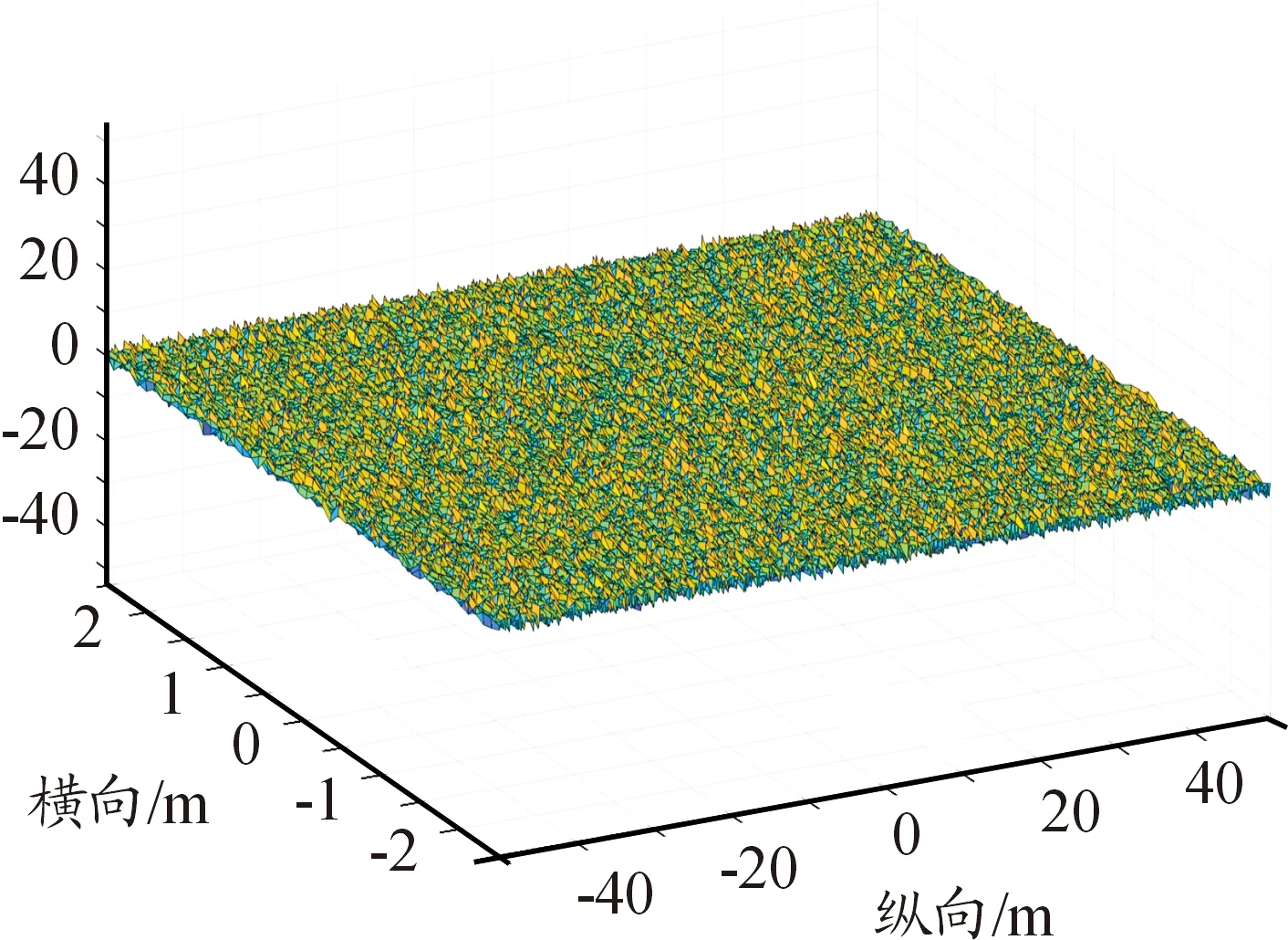
圖3 A級路面譜

圖4 D級路面譜

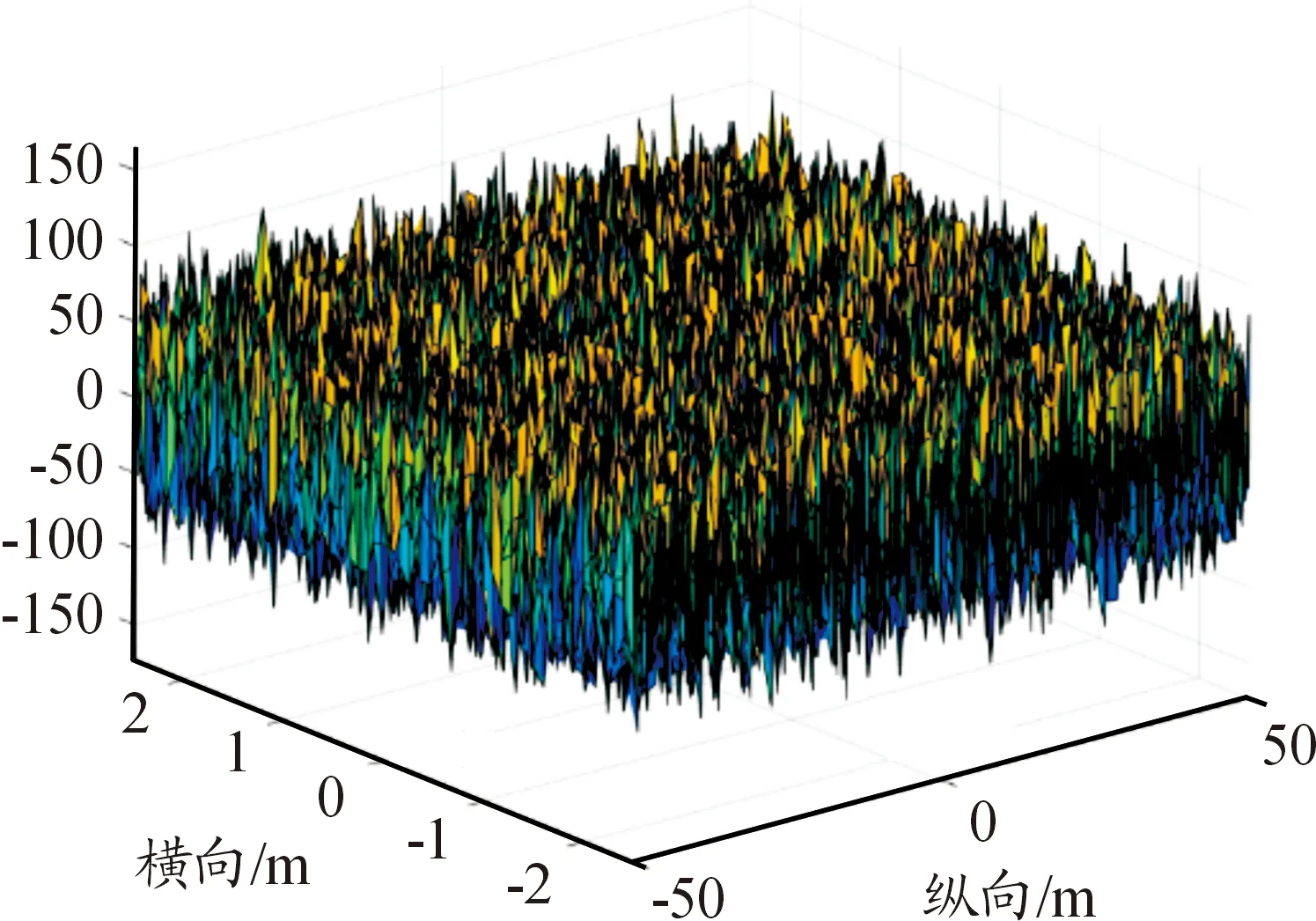
圖5 F級路面譜

3 機電聯合建模

伺服電機具有效率高、功率密度密集以及易于控制的優點，本文研究的火箭炮系統以伺服電機為執行機構。火箭炮在瞄準過程中，發射箱的調炮過程及對打擊目標的動態跟蹤全部依托于位置伺服系統。火控計算機給出目標方位指令，并將其發送給驅動計算機，繼而計算伺服電機相應的模擬電壓量，實現動態跟蹤。伺服電機的控制采用電流-速度-位置三閉環控制。

PID控制結構簡單，算法簡單易懂，參數含義明確，具有較好的魯棒性，并且對于精確模型的要求低，所以在實際工程中，是一種應用最為廣泛的控制算法。

假設多管火箭炮俯仰和回轉機構的指令角度為qd=[θdφd]T，則誤差為：

e=qd-q

根據PID控制律，則多管火箭炮俯仰、回轉控制器設計為：

式中：Kp為比例系數;Ki為積分時間常數的倒數；Kd為微分時間常數。在Matlab/Simulink中建立PID控制模塊，并將Adams中的動力學模塊聯合，聯合仿真系統模型如圖6所示。

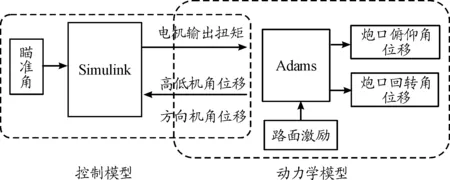
圖6 聯合仿真系統模型框圖

4 仿真與分析

本文針對行進間發射過程中不同路面不平度對PID控制的影響進行研究。將車載火箭炮行駛速度設置為50 km/h，火箭炮位置伺服系統由0°調炮至1 rad，需滿足如表2所示指標，分別計算A、D、F級路面行進間發射時，不同的路面等級對PID控制的影響。由于車輛前0.5 s為加速過程，本文在0.5 s之后車輛勻速運行時，給定角度指令信號，并在3 s時發射一枚火箭彈。仿真過程中采用四階龍格庫塔數值積分方法，仿真時間步長0.000 1 s，通過實驗湊試法，PID參數已達最優。圖7～圖11為車載火箭炮在不同路面等級下PID控制俯仰角度值。

表2 火箭炮伺服系統性能指標

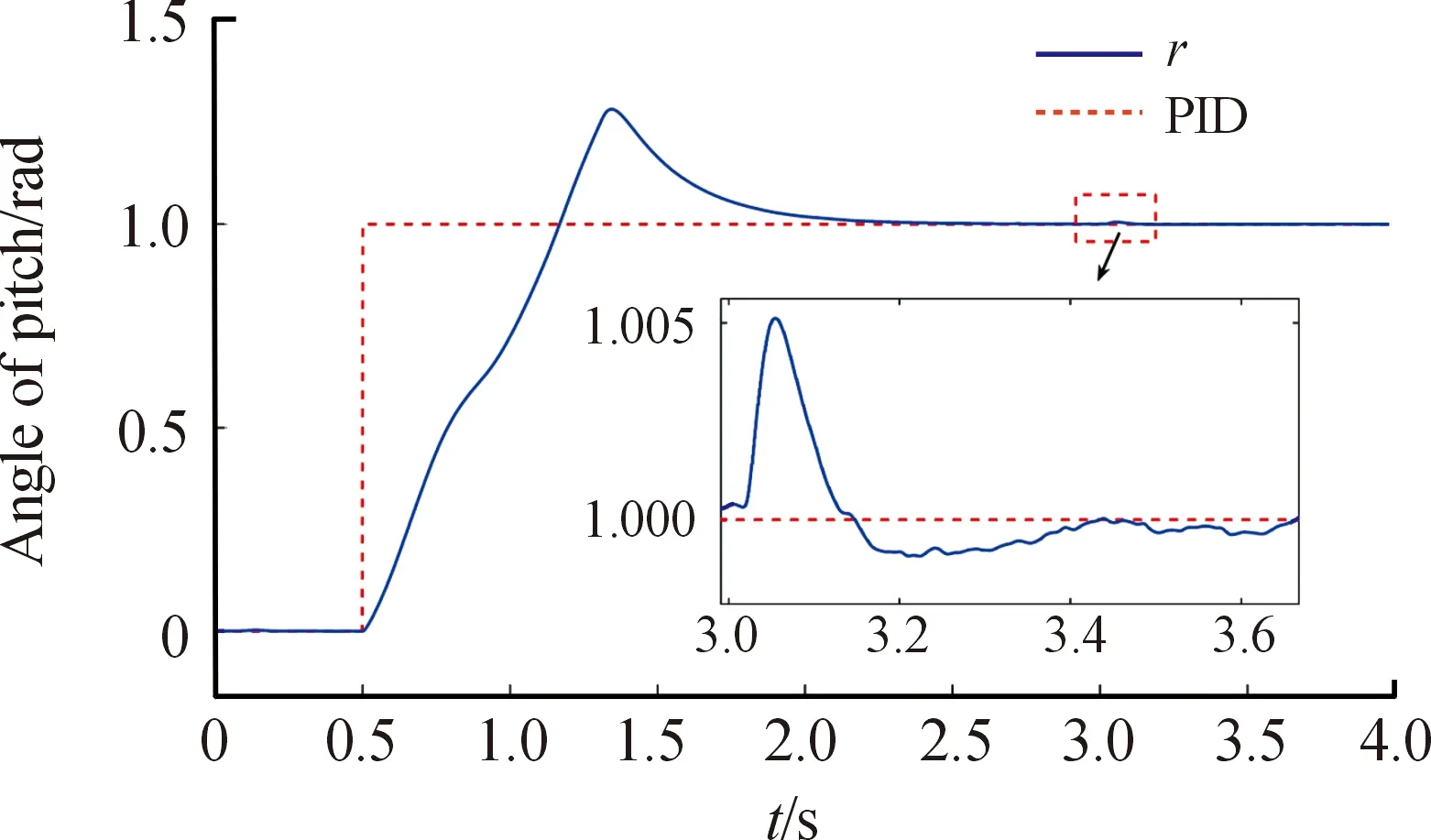
圖7 A級路面高低角變化曲線

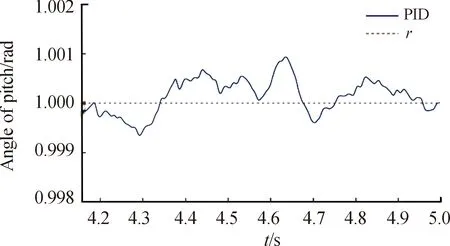
圖8 A級路面平穩運行高低角變化曲線

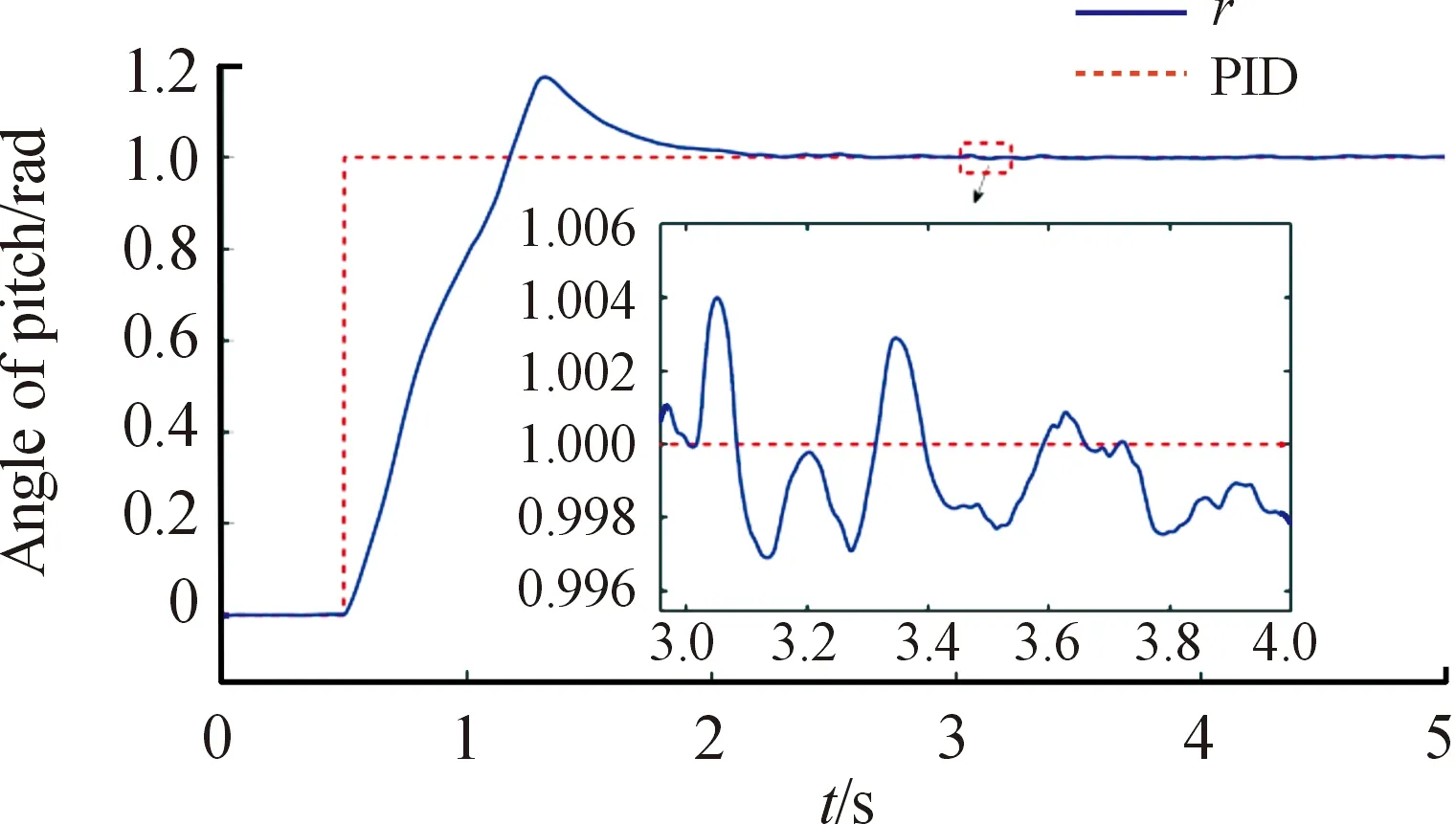
圖9 D級路面高低角變化曲線

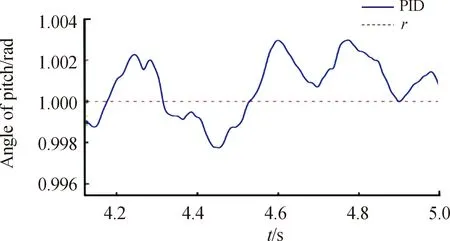
圖10 D級路面平穩運行高低角變化曲線

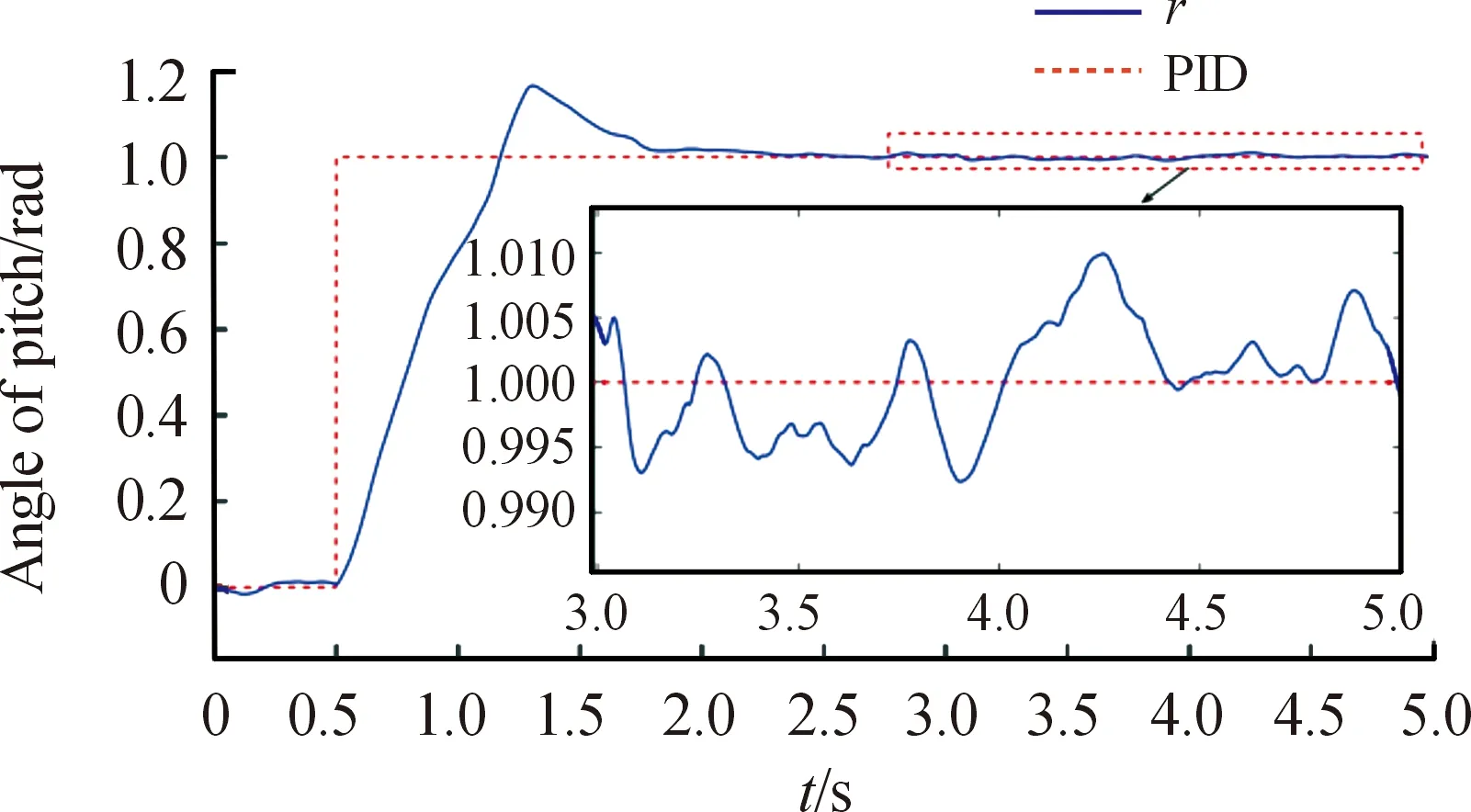
圖11 F級路面高低角變化曲線

從圖7、圖8可以看出在A級路面行進間發射，PID控制方式可以得到良好的控制精度。由于火箭彈燃氣流沖擊造成的擾動為4.78 mil，且在0.4 s內恢復到指定角度；由路面不平度造成的擾動最大為0.95 mil，滿足性能指標要求。由圖9～圖11可以看出，隨著路面不平度的增大，PID控制精度下降。其中D、F級路面下按照50 km/h的速度行進，俯仰角度最大控制誤差分別為2.89 mil、9.55 mil。通過表3表明，PID控制下為了同時兼顧快速性和穩定性，在實際的控制過程中出現超調，且隨著路面不平度的增大，超調量增大，調節時間增長。

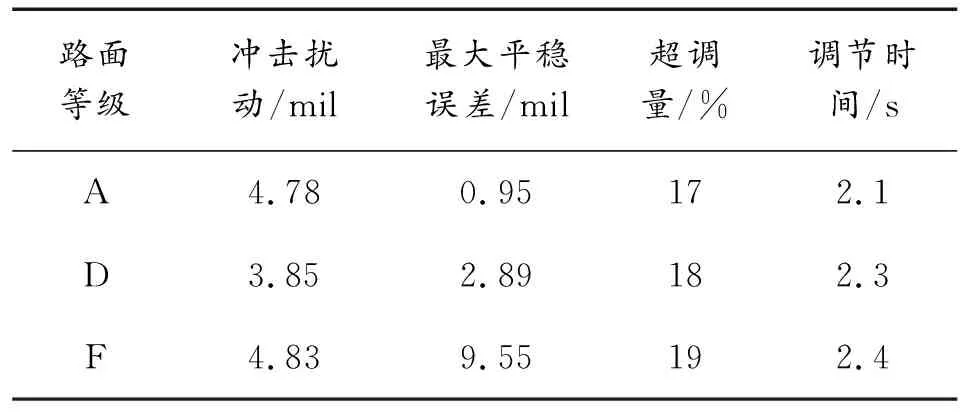
表3 不同等級路面下各參數對比

5 結論

1) PID控制作為一種經典的控制方式，在激勵較小的A級路面可以達到精確的控制效果，但其控制精度隨著路面不平度的增大而降低，驗證了火箭炮在優質工況下行進間發射的可行性。

2) PID控制為了兼顧快速性和穩定性會出現超調，且超調量隨路面不平度的增大而增大。