基于實驗數據同化的湍流模型常數標定：含濾網蒸汽閥門通流特性數值預測

房培勛，何創新，徐嗣華，王 鵬，劉應征，，*

(1. 上海交通大學 中英國際低碳學院，上海 201306；2. 上海交通大學 機械與動力工程學院 葉輪機械研究所，上海 200240；3. 上海汽輪機有限公司，上海 200240)

0 引 言

蒸汽調節閥是蒸汽動力系統的重要控制部件。通過調整調節閥的開度，可以控制動力系統的蒸汽輸入，使系統實現能量平衡。準確掌握蒸汽調節閥通流特性對蒸汽動力系統設計和運行至關重要，既有助于工程設計人員在系統的設計階段完成閥門選型，優化系統構造，又能方便系統運行控制人員快速、準確地完成動力系統的調節，保證動力系統的穩定高效運行。目前主流的調節閥通流特性研究方法大都采用雷諾時均（Reynolds Averaged Navier-Stokes, RANS）計算流體力學（Computational Fluid Dynamics, CFD）模擬，使用湍流模型封閉方程。然而，湍流模型計算的準確性高度依賴合理的模型常數，而這些常數多由平板邊界層、自由剪切流等經典流動標定而來，這顯然難以滿足調節閥內部復雜流場預測的要求。通常，RANS模型計算只能定性描述閥門通流特性，定量誤差則普遍高于10%[1-3]。毫無疑問，選擇使用合適的湍流模型常數，對于準確預測調節閥門通流特性非常重要。

采用實驗數據驅動的相關算法優化湍流模型常數是常用的優化策略[4]，其中數據同化則是最重要的方法之一。數據同化，是實驗觀測和模型預測的融合，其三大要素為預測模型、觀測數據和同化算法。該方法在模型預測中融入觀測數據而改變模型運行軌跡，最終達到優化模型性能、提高預測精度的目的[5]。數據同化最早運用于氣象預報[6]，而后擴展至地質[7]、水文[8]、系統監測[9]等領域。近些年，數據同化被引入了湍流數值模擬，成為優化湍流模型常數的重要方法。Hiroshi Kato[10]等提出了基于數據同化的湍流模型常數標定方法。該方法將實驗測量數據作為觀測，運用集合變換卡爾曼濾波（Ensemble Transform Kalman Filter, ETKF）算法修正k-ωSST模型的a1常數。Margheri[11]等基于數據同化方法研究不同RANS模型中常數的不確定度，其結果表明：相較k-ωSST模型，預測參數對k-ε模型相關常數的敏感度要更高。Yang[12]等用數據同化方法量化k-ω-γ-Ar四方程湍流模型常數的不確定度，其結果表明：預測變量對該模型的不同常數有不同敏感性，且對于不同案例，并不存在普適的常數向量。因此，數據同化方法可以有效標定湍流模型矩陣。然而，在應用數據同化方法標定調節閥通流特性模擬的模型常數時，需要充分考慮常數向量的適用性。

蒸汽調節閥內部的流動極為復雜，且在不同運行工況下呈現不同特征。Wang等[13-15]研究了蒸汽調節閥內部的不穩定流動，發現閥內流動中存在射流、回流、旋渦等多種復雜現象。曾立飛等[16]研究了雷諾數對于調節閥模化試驗的影響。結果表明其所研究的閥門呈現出附閥座流、沖擊射流和充滿流三種情形。Domnick[17]等對調節閥內流場的研究發現了三種流態：大開度、極大壓比條件下的擴散器充滿流動，極小開度、中小壓比條件下的壁面附著流動和較小開度、小壓比條件下的分離流動。調節閥內部流動形態的多樣性，說明難以存在普適模型常數向量。本文所研究的蒸汽閥，內部結構緊湊，閥內流場復雜，顯然需要結合閥內流態找到針對性的湍流模型常數。

本文實現了數據同化技術在工業化情景下的應用。以含濾網蒸汽調節閥為研究對象，采用k-ωSST模型數值模擬，結合通流特性實驗測量結果進行集合卡爾曼濾波的數據同化，修正了預測模型的常數向量。按照閥門開度的區別，標定了3組SST模型常數向量，并進行了相關的驗算和流場參數對比，分析了標定常數的適用性，為調節閥數值模擬優化提供了重要參考。

1 數學原理

1.1 湍流模型方程

RANS模型因其對計算時間和硬件成本的低要求，成為了閥門通流特性的重要預測工具。在眾多RANS模型中，由Menter提出[18]的k-ωSST模型，是一種綜合標準k-ε和標準k-ω的兩方程混合模型。該模型既具有標準k-ω善于預測邊界層內部區域流動的優點，又有標準k-ε善于預測外部區域和自由剪切流動的優勢。因而，本文采用k-ωSST模型作為數值模擬的基礎模型，并結合閥門特性實驗測量結果對模型常數進行重新標定。

SST模型k-ω部分微分方程為：

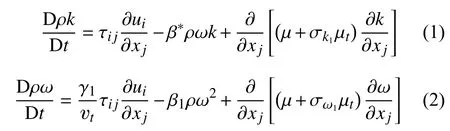
SST模型k-ε部分微分方程為：

式（2、4）中渦黏度項vt定義為：

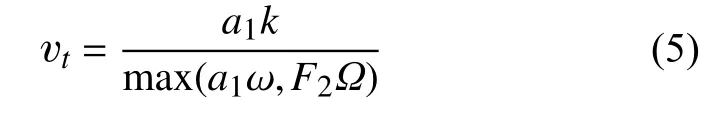
式中，Ω為渦度的絕對值，F2為一與流場相關的函數。

引入混合系數F1，可將二者綜合，得到k-ωSST模型的微分方程：

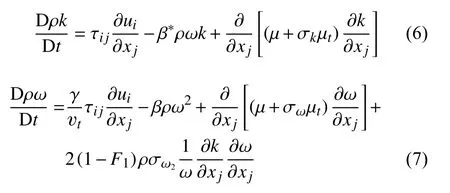
其中，

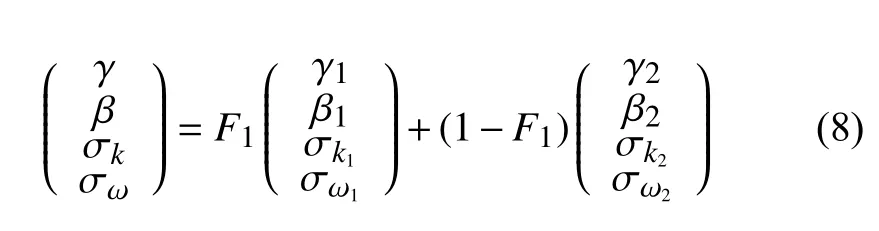
SST模型的F1是一個調整k-ω部分和k-ε部分在整體模型中占比的系數。在靠近壁面時，F1趨于1，此時SST模型趨于k-ω模型；遠離壁面時，F1趨于0，此時SST模型趨于k-ε模型。由此，SST模型實現了在不同區域對k-ω部分和k-ε部分占比調整，從而融合二者的優勢。SST模型中共涉及到8個常數，其默認值如表1所示。本文將重新標定表1列出的模型常數。

表1 SST模型常數默認值Table 1 Default SST model constant

1.2 數據同化

數據同化過程實質為反演過程。預測模型的形式確立了預測參數與模型常數間的映射關系（預測），而數據同化則是采用一定算法（同化算法）解析映射關系（分析），并綜合相關測量數據（觀測）反推和標定模型常數（更新）。

本文數據同化所采用的預測模型為SST模型，觀測數據為實驗所測得的閥門入口流量數據，同化算法主要采用集合Kalman濾波（Ensemble Kalman Filter,EnKF）算法[19]重新標定SST模型的相關模型常數，詳細過程將于下文說明。

1.2.1 集合卡爾曼濾波

數據同化所使用的算法種類繁多，包括三維變分、四維變分、粒子濾波（Particle Filter, PF）、擴展卡爾曼濾波（Extended Kalman Filter, EKF）、集合卡爾曼濾波、集合變換卡爾曼濾波（Ensemble Transform Kalman Filter, ETKF）等。變分類同化一般多依靠預測模型的伴隨方程進行求解[20]，不適合復雜模型的優化。粒子濾波對狀態空間的搜索使用大量的隨機樣本[5]，這容易導致算法計算量大，且大量資源浪費于無用的粒子上。而卡爾曼濾波類同化則相對簡單地獲得數值模型的先驗統計信息[21]，適合本文的湍流數值模型這類復雜模型的優化。其中，集合卡爾曼濾波算法由Evensen[22]于1994年提出，是該類同化方法中最常用的算法之一。該算法從經典卡爾曼濾波和擴展卡爾曼濾波算法發展而來，能夠結合觀測數據完成對預測模型的修正。同時，集合卡爾曼濾波算法采用了蒙特·卡洛方法的誤差統計，使其不再具有經典卡爾曼濾波算法對于線性系統的要求和擴展卡爾曼濾波用于高階非線性問題時存在較大誤差的缺陷，在高階非線性領域亦可使用。同時，相關研究指出，對于湍流數值模型優化問題，集合卡爾曼濾波的優化性能優于集合變換卡爾曼濾波[10]。綜上所述，針對具有高階非線性特點的湍流問題的數值模型優化，本文采用集合卡爾曼濾波算法作為同化算法。

算法考察對象為如下的非線性系統：

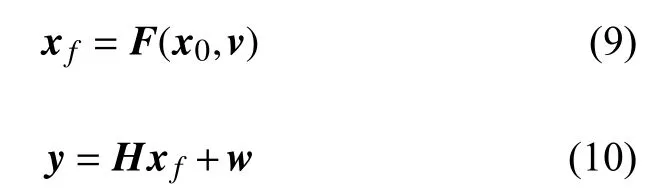
其中，式（9）為非線性系統的預測方程，式（10）為觀測方程。式中為系統狀態參數的預測，為觀測，x0為系統初始狀態，v和w分別為系統噪音和觀測噪音，F為預測模型，H為觀測函數。

算法的主要流程包括預測過程和分析過程：

1）預測過程。預測過程中，每個集合成員中的狀態參數向量將從初始狀態開始利用SST模型迭代計算，直至湍流數值模擬計算收斂。狀態參數由以下公式給定：

其中，預測模型F為SST模型方程，集合成員狀態參數的形式為q為預測的入口體積流量，θ=為湍流模型常數向量，記錄了表1所述的8個常數的取值。

集合成員的均值由下式給出：

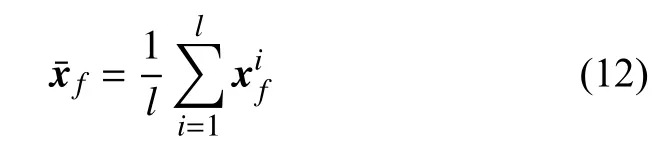
此處，上標i指集合成員的序號，l為集合成員總數，為集合成員均值。

2）分析過程。這一步是集合卡爾曼濾波的核心。算法通過整合觀測信息的不確定度和集合成員的統計信息，從而確定卡爾曼增益并完成對集合成員的更新。該步驟的過程如下：

a. 預測誤差的分析：

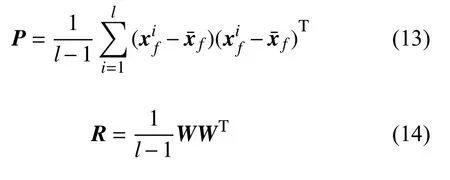
其中，

b. 卡爾曼增益計算：

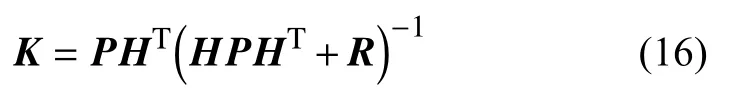
c. 更新集合成員：

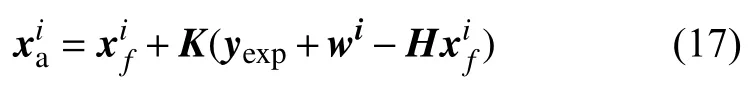
對應新集合成員的均值：

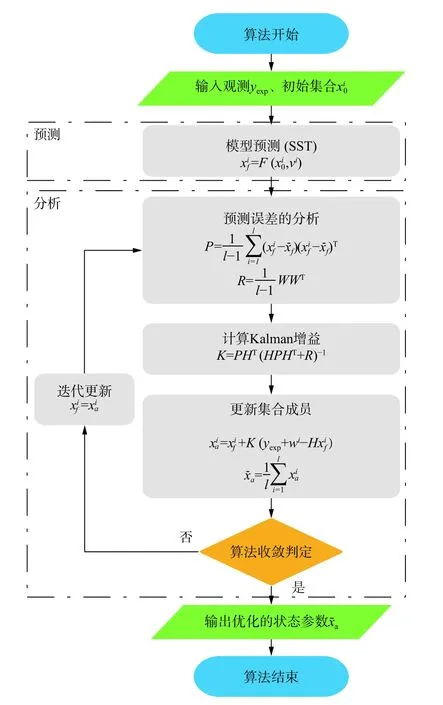
圖1 集合卡爾曼濾波算法流程圖Fig. 1 Flow chart of EnKF Algorithm

1.2.2 模型常數標定

本文模型常數的標定基于集合卡爾曼濾波的數據同化方法。其中，集合的狀態矩陣為:

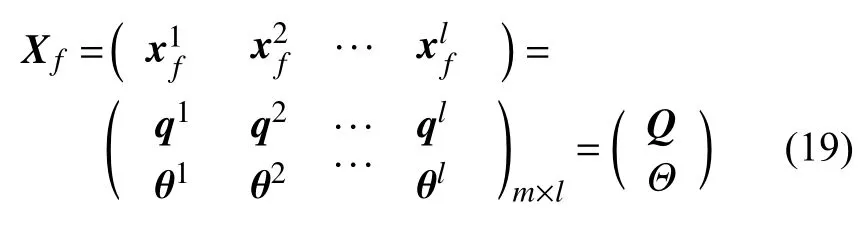
實驗流量觀測數據為：

同化觀測矩陣為：

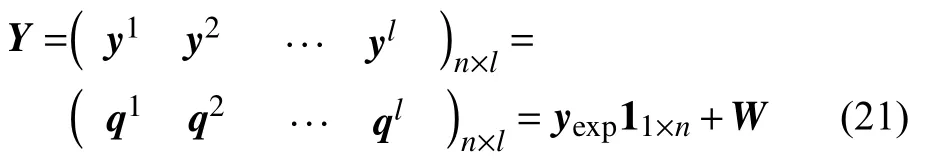
觀測函數矩陣H為：

其中，1M×N為M行N列元素全為1的矩陣，IN為N階單位矩陣，0M×N為M行N列元素全為0的矩陣。成員總數l=100。標定過程先通過拉丁超立方抽樣

湍流模型常數標定流程如圖2所示，選取的集合（Latin Hypercubic Sampling, LHS）生成湍流模型常數的100個樣本，并使用預測模型，即SST模型預測一定工況下閥內流動，獲得對應的100組預測流量。二者按照式（19）整合，即為算法的初始狀態矩陣。此后，結合由實驗獲得的對應工況下的流量觀測數據，將二者共同輸入集合卡爾曼濾波算法，經過分析步驟多次迭代更新，可獲得最優的模型常數，即為該工況觀測數據標定的模型常數。最后，將標定的常數應用于相同或不同工況進行重新計算驗證，以評判該湍流模型常數的可靠性和適用性。

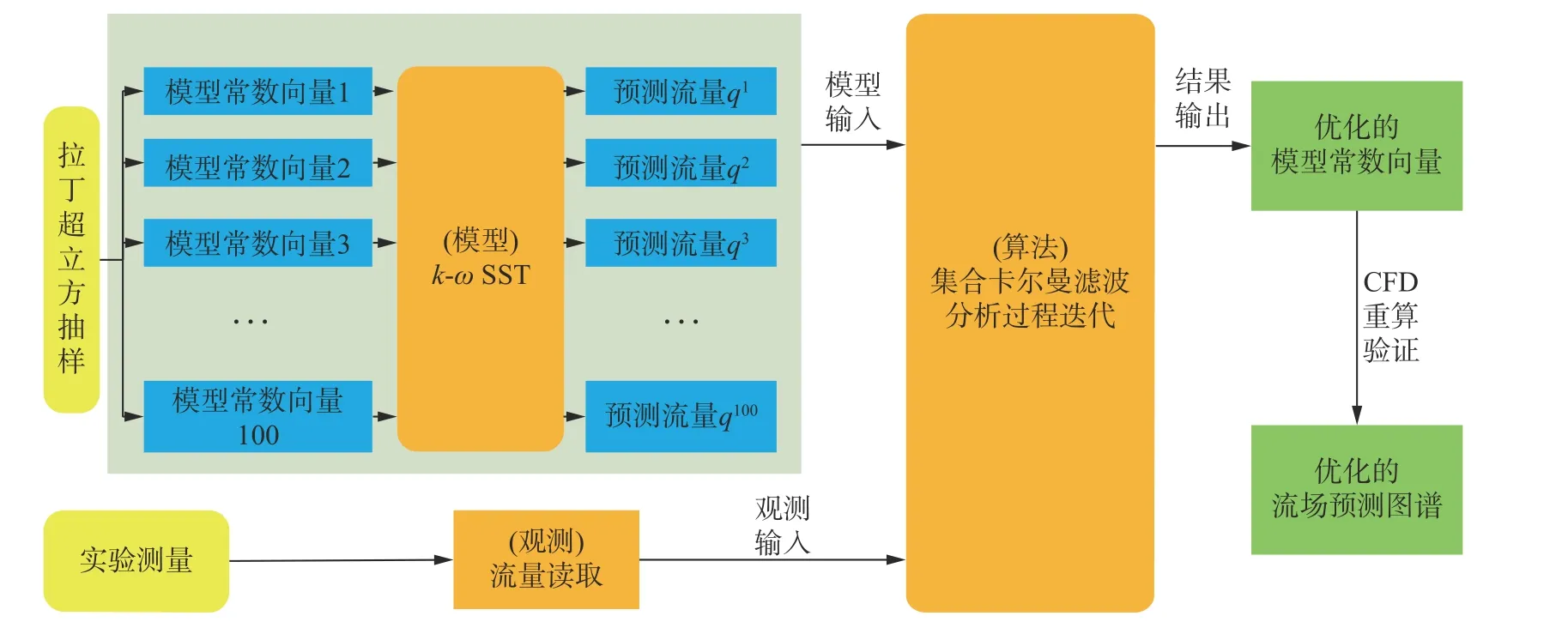
圖2 基于實驗數據同化的湍流模型常數標定過程Fig. 2 Model constant calibration procedure based on experiment data assimilation

可以看出，本文的湍流模型修正方法具有的兩大優勢。首先，該方法運用了數據同化方法，它是一類數據驅動的模型常數優化方法，可以實現對觀測數據的充分利用，且實現上也相對簡單；同時，本文所使用的集合卡爾曼濾波算法可以綜合考慮模型預測和實驗觀測存在的誤差，從而給出更準確的估計，相關結果更具有實際意義。

2 計算實例

2.1 研究對象

本文的研究對象為如圖3所示的蒸汽調節閥。圖3（a）展示了閥門內部及附加管道流體域的正等測視圖，圖3（b）展示了閥門的z= 0截面示意圖，其中閥內流體的路徑如圖中箭頭所示。整個閥門結構包括調節閥結構（上）和主閥（截止閥）結構（下），二者具有共同的閥座。調節閥結構的閥腔與下游出口管道相連，閥塞（紅色）作為實驗的研究對象可以上下移動，達到調節閥組開度的目的。主閥結構的閥腔與上游入口管道相連，閥塞（藍色）在整個實驗中固定于開度最大的位置，從而使主閥始終保持全開狀態；附加的濾網則位于在主閥閥芯的外側，起到去除流體內雜質和整流的作用。

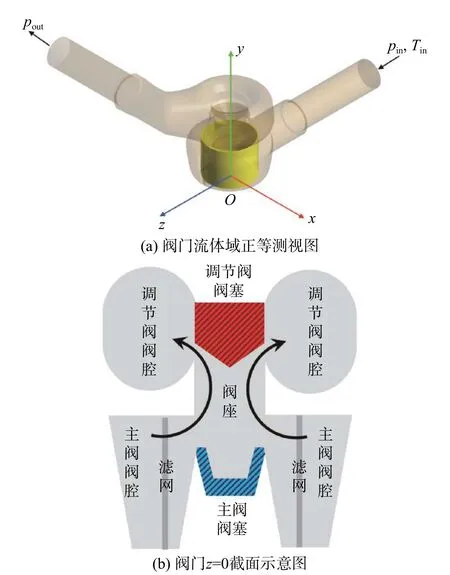
圖3 閥門幾何結構示意圖Fig. 3 Geometry sketch of valve

為了獲取用于數據同化觀測輸入及后續驗證的相關數據，本研究相關的通流特性實驗已于前期進行。整體的管路圖如圖4所示，其中入口控制閥、出口調節閥用于調整被測閥門入、出口的壓力，蒸汽加熱器用于恒定閥門入口蒸汽溫度并確保閥內的蒸汽始終具有一定的過熱度。本研究中所涉及到的重點研究區域為圖中虛線框內區域。實驗中閥門保持一定開度（大/中/小），入口（溫度計/壓力計3）通入總壓pin，總溫Tin的蒸汽，出口（溫度計/壓力計4）保持靜壓pout，由入口處安放的體積流量計讀取入口體積流量q。相關實驗數據由表2給出。表中pout/pin為閥門的壓比，即出口壓力與入口壓力的比值；q/qmax為 閥門的標準化體積流量，其中qmax為實驗中出現的最大流量（M-2工況對應流量）。

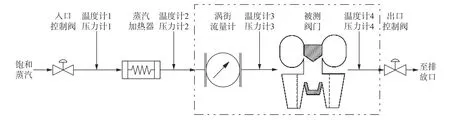
圖4 通流特性實驗管路Fig. 4 Pipeline of flow characteristic experiment

表2 閥門實驗數據Table 2 Valve experiment data

2.2 計算設置

本文中數值模擬部分基于商業軟件 ANSYS CFX。計算的流體域如圖3（a）所示，包括兩側的出入口管道。計算的設置為穩態求解，基礎湍流模型為SST模型，工作介質選用理想水蒸氣。由于原型的濾網結構過于精細，無法完全按照幾何結構進行模擬，因而采用文獻[23, 24]中推薦使用的多孔介質模型處理。邊界條件中入口邊界條件總壓pin，總溫Tin，出口邊界條件靜壓pout，二者均設置為亞聲速流動。CFX求解器的CFD算法為有限體積法（Finite Volume Method,FVM），在本文中求解器的對流項差分格式設為二階迎風格式。經過網格無關性相關驗證，本文采用節點總數約100萬的網格進行相關數值計算，從而在保證數值精度的前提下提高計算效率。

3 結果與討論

3.1 外特性對比

本文的數值計算邊界條件依據相關實驗測量的出入口數據設置。運用1.2.2節提出的模型常數標定方法，可由實驗數據標定出三組模型常數矩陣，相關標定結果見表3，其中常數1，常數2，常數3分別對應大、中、小開度的閥門實驗工況。

表3 通過數據同化得到的湍流模型常數向量Table 3 Calibrated model constant vectors using data assimilation

為檢驗標定參數的可靠性及可拓展性，文中采用兩種模型常數向量CFD驗算的相關方案，具體見表4。方案1為按開度分組驗算工況，每組僅使用組內工況標定的常數向量驗算；方案2為所有驗算工況僅使用中開度工況（M-1）標定的常數向量（常數2）驗算。將相關的驗算結果與實驗記錄對比，可得到對應的預測流量及誤差，相關標準化分析結果于圖5給出。

表4 模型常數向量驗算方案Table 4 Validation cases for model constant vectors

從圖5可看出，方案1選取的模型常數獲得了最小的誤差，且所有誤差均小于默認SST模型的預測誤差。這一點說明每一組工況的計算選擇基于自身內部工況標定的常數的方案1是可行的。分析方案2，發現調節閥開度水平偏離常數的標定來源工況開度水平時，無論偏大還是偏小，都會出現顯著的誤差。這說明了最優湍流模型常數的選取需要依據閥門開度的大小進行。

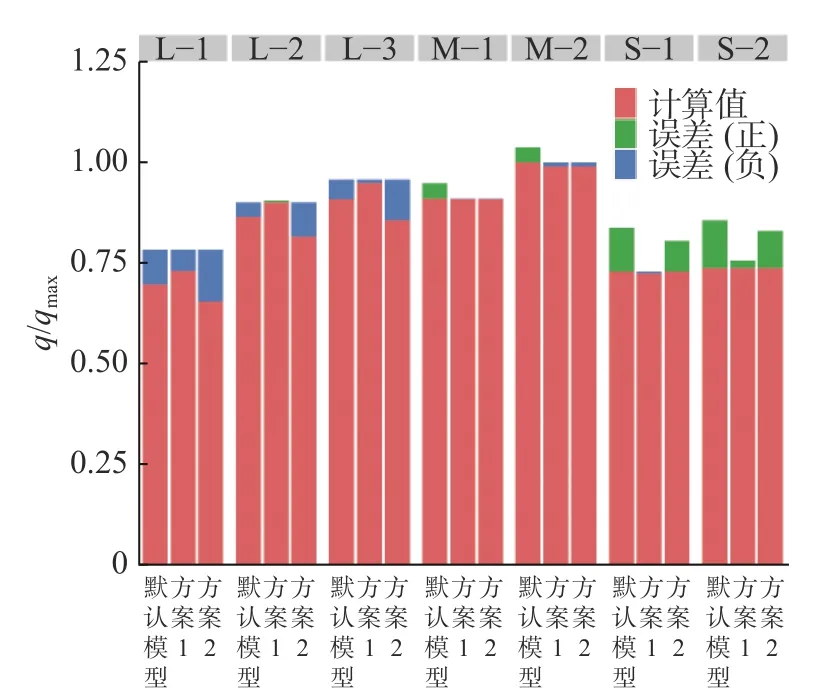
圖5 不同方案預測的標準化流量及與實驗對比誤差Fig. 5 Normalized flow rate by different prediction methods and relative errors against experimental measurements with different methods

3.2 內部流場分析

為了從根本解釋以上現象，本文分析了L-1、M-1和S-1三個工況的內部流場。在本文研究的范疇內，閥門在相似的開度、不同壓比下的計算結果類似，因而相關流場不重復列舉。

3.2.1 修正前不同工況閥內速度場對比

圖6展示了默認常數設置下閥內流動形態。由圖6（a）可以看出，閥內高速區域的范圍是不同開度下閥內速度場的重要區別。大開度下，如圖6（a）左，高速區域填充了整個閥座和主閥閥口區域，并可以一直追溯到濾網內側箭頭指示位置。中開度下，如圖6（a）中，高速區域僅可追溯到調節閥閥口，閥座內出現了“空心”。小開度下，閥內的高速流動區域僅填充了閥座內靠近壁面的小部分區域。此外，調節閥閥腔內的流動也存在顯著區別。盡管圖6（a）中三種開度下調節閥閥腔內高速流動區域均呈現圓環狀，但該區域的厚度卻有顯著差異：大開度的高速區域厚度最高，中開度次之，小開度最低。

圖6（b）展示了調節閥閥口下游鄰域的速度場和流線分布。大開度下，調節閥閥塞接近全開位置，其頂面與下游空腔壁幾乎平齊，因而閥口下游高速區域較為寬廣，流線方向恒定，且與壁面間幾乎不存在低速帶；中開度下，與前者類似，下游高速區域的流線方向較為恒定，但是閥塞錐面與下游壁面的相對偏離，導致高速區域與壁面間出現一個明顯的低速帶，且低速帶一直延伸至壁面彎曲處；小開度下，下游高速區域在靠近閥口處與壁面明顯分離，在遠離閥口處出現明顯的流線方向改變，導致很快出現再附著的現象。

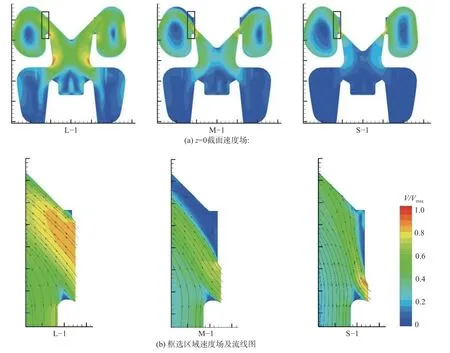
圖6 默認SST模型預測的閥門流動形態Fig. 6 Valve flow pattern predicted by default SST model

以上現象說明不同開度水平下閥內流動形態存在明顯的差異。流動形態的顯著不同，必將導致最適模型常數存在一定的差異性，因不同閥門開度下最優的常數向量也必將不同。然而，以上的分析僅基于默認常數的計算，更可靠深入的分析還需要依據同化修正后的流場進行。

3.2.2 同工況修正前后閥內速度場對比

圖7～圖9分別展示了M-1、S-1、L-1三種工況、不同模型常數下、閥門z= 0截面的標準化速度場對

圖7 M-1工況z = 0截面不同模型常數預測的速度場Fig. 7 Predicted velocity field using different model constants on plane z = 0 at operating condition M-1

由圖8（b）可以看出，運用方案2修正的閥內流場的均勻性被一定程度上提升，整體復雜程度類似圖6（b），且高速區域在相似位點中斷。由圖8（c）則可以看出，運用方案1修正的閥內流動的均勻性被進一步提高。調節閥閥口下游的高速區呈貼壁流態，且于極短比。三個圖（a）中默認常數的情形已于3.2.1節討論，此處不再贅述。

圖8 S-1工況z = 0截面不同模型常數預測的速度場Fig. 8 Predicted velocity field using different model constants on plane z = 0 at operating condition S-1

由圖7（b）可以看出，修正后的流場存在兩點顯著區別：一是調節閥閥口最大流速一定程度的降低，且在下游鄰域，流動不再分離，轉化為貼壁流動；二是調節閥閥腔內的環狀貼壁流動被削弱，流體沿著壁面到達圖7（b）箭頭所示位置時速度顯著降低，呈現被截斷的狀態。對比二者綜合而言，修正后的閥內流場的高速區域更小更規則，流動更簡單、更均勻。的距離內耗散，與低速區融合。綜合對比，圖8（a）到圖8（b）到圖8（c）流場的均勻性被逐步提高，閥內高速流動區域向閥口下游的流向延伸距離依次遞減。

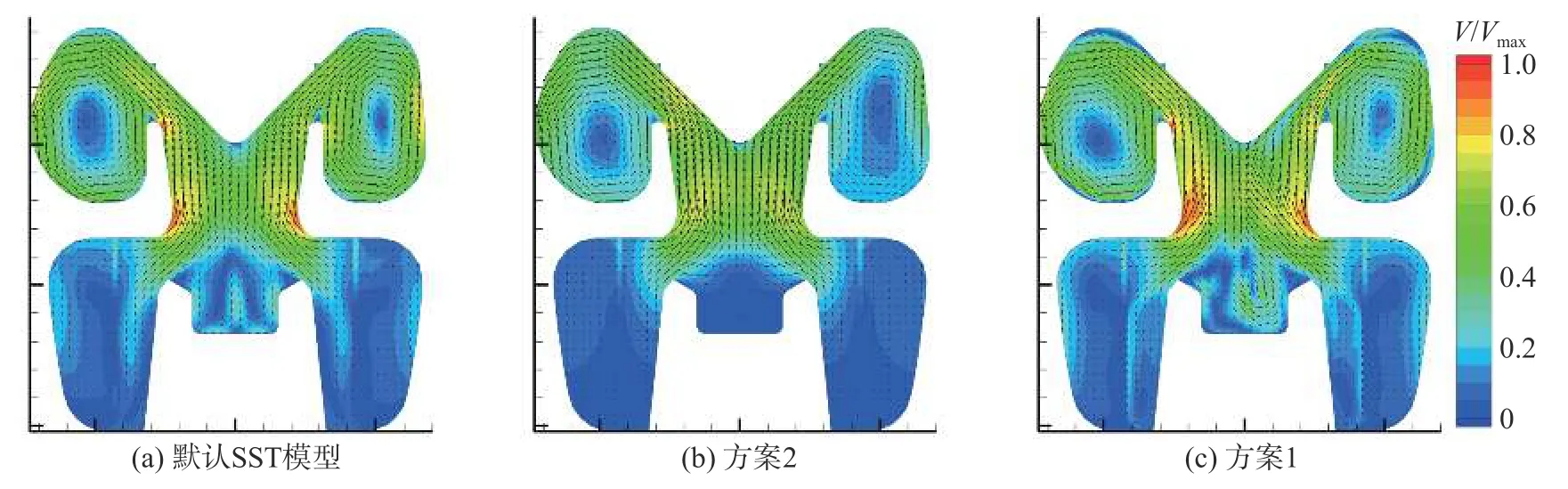
圖9 L-1工況z = 0截面不同模型常數預測的速度場Fig. 9 Predicted velocity field using different model constants on plane z = 0 at operating condition L-1

由圖9（b）可以看出，采用方案2修正的閥內流場的均勻性被一定程度上提升，且調節閥閥腔內的旋渦狀流動被截斷，貼壁流動到達一定區域時速度顯著降低，整體復雜程度與圖6（b）相似。由圖9（c）可以看出，采用方案1修正的閥內流場與圖9（b）的趨勢完全相反。閥內流動的均勻性被削弱，出現了更多的旋渦狀結構；調節閥閥腔內的旋渦狀流動不僅保持存在，且相對圖9（a）更加復雜，出現多次分離和附著。因而，大開度情形下，默認模型和方案2的預測均無法捕捉閥內流場的細節。

分析以上現象可知，采用單一模型常數向量（默認SST模型、方案2），預測的流場具有相似的均勻度；而合理采用多種模型常數向量（方案1），預測的流場的均勻性隨著開度的降低而增加。單一模型常數向量無法準確捕捉不同開度下閥內變化的速度復雜度，即無法實現對閥內速度場分布的合理預測。因而在通流特性預測上呈現出較大的局限性；而合理采用多種模型常數向量分別求解，可以適應多開度下閥內流場速度分布預測的需求，從而提高閥門數值模擬預測的準確度。

3.2.3 修正前后閥內渦黏度對比

在利用RANS求解湍流問題的過程中，雷諾應力項的引入使得原方程組失去封閉性從而無法求解，而湍流模型的提出正是為了解決這一問題。湍流模型包括的物理項有對流項、生成項、耗散項等，在充分發展的湍流流場的控制區域內，湍流的流入、生成、耗散達到平衡。而這些湍流模型中的常數則是用來標定這些物理項相對貢獻的大小，因而對前者的重新標定會打破原先的平衡并使其逐漸轉移至一個新的平衡，這將改變流場內重要的湍流物理量的預測。其中，渦黏假設是一類湍流模型（渦黏模型）的重要處理方法，而渦黏度υt則是對湍流模化以后影響時均流場的關鍵湍流物理量。因而，分析預測的閥內渦黏度分布，有利于理解模型常數修正對閥內流動預測優化的實質作用。

圖10展示了不同設置下z= 0截面預測的標準化渦黏度場，標準化渦黏度定義vt,n為：

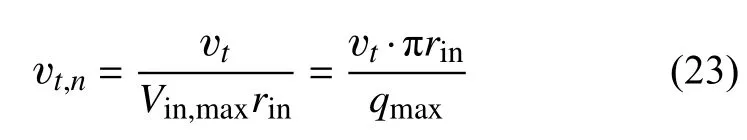
式中，rin為閥入口半徑，作為特征長度；Vin,max=為最大流量下入口平均速度，作為特征速度。

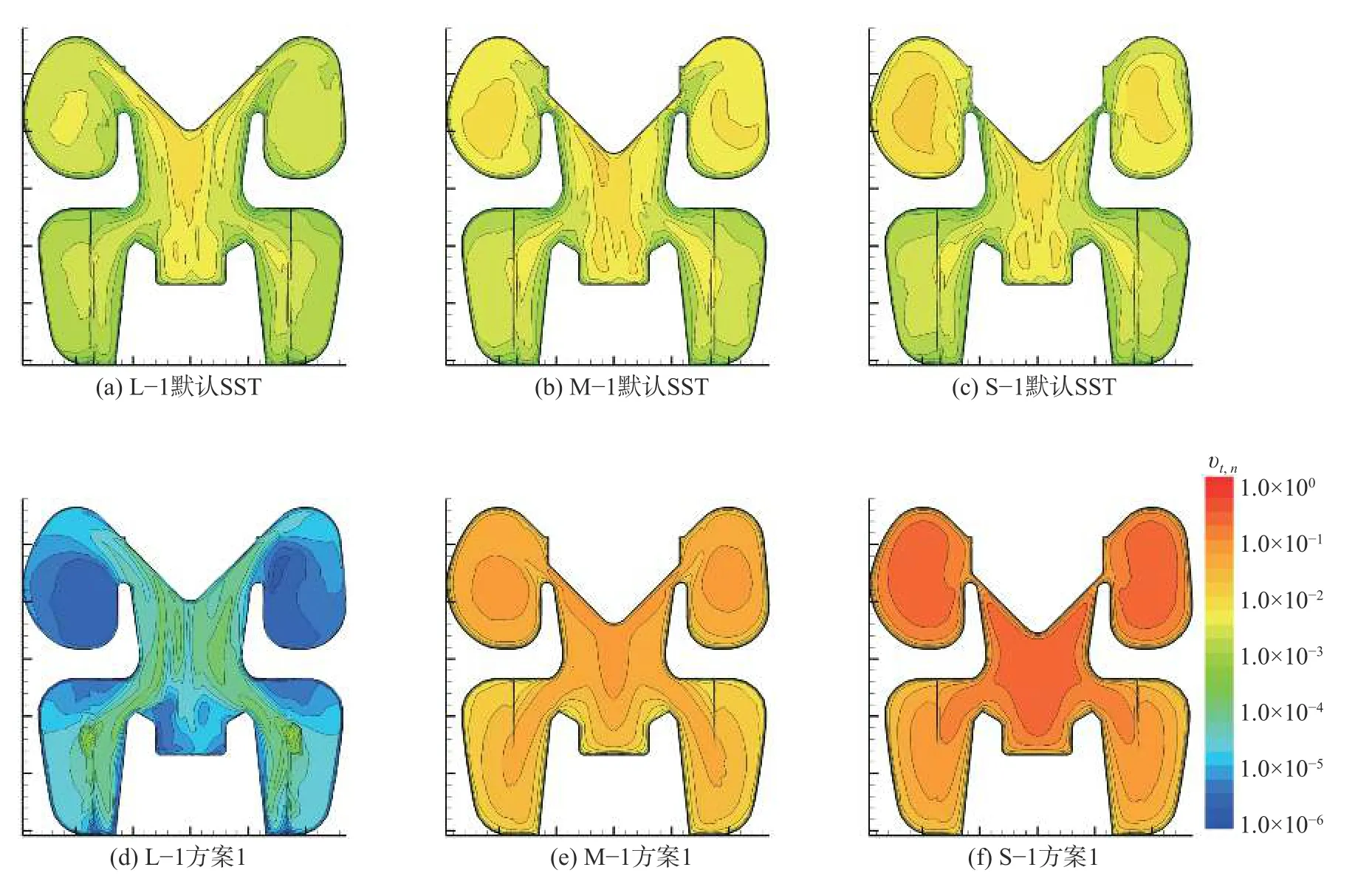
圖10 z = 0截面不同模型常數預測的標準化渦黏度Fig. 10 Predicted normalized eddy viscosity using different model constants on plane z = 0

由圖可得，采用默認常數模擬時，所有開度預測的的無量綱化渦黏度均處于10-4至10-2的水平；而采用標定的常數按方案1計算，不同開度預測的結果具有不同的渦黏度等級。大開度預測的渦黏度的數量級為10-6至10-4，中開度預測的渦黏度的數量級為10-2至10-1，小開度預測的渦黏度的數量級為10-1至100。文獻[25]指出，當閥門的開度發生變化時，閥內特征位點的湍流強度也會隨之變化；相比于較大開度下的情形，較小開度下特征位點的湍流強度更高。依據渦黏模型的相關理論，渦黏度表征湍流對時均場分布的貢獻。因而，可推斷默認模型未實現對不同開度下閥門流場的湍流特性的準確預測，從而導致流量預測誤差的出現。相反，采用修正后的模型常數，大開度的渦黏度預測量明顯降低，而中開度和小開度情形卻明顯提高。從定性上看，顯然這種對不同開度下獲得不同閥內湍流特性的預測是更合理的，它能夠體現不同開度下湍流特性的差異，與閥內流動的特征更一致。

結合前文分析，可以看出速度場與渦黏度場間的關聯性。基于默認常數，不同開度下閥內流動雖展現出多種不同的流態特征，但復雜程度相當；對應的，默認模型預測的閥內的渦黏度場強度相似。采用方案1，不同開度下閥內流動的復雜程度隨著開度增加而逐漸提高；對應的，方案1預測的閥內渦黏度隨著開度的提高而逐漸降低。更高的渦黏度表征湍流對時均流場更強的影響，一般來說促進湍流摻混，從而提高閥內流動均勻性。顯然，對湍流摻混的修正，會改變閥內流動速度場的預測。由于閥門入口體積流量是閥門質量流量和入口處流體密度的函數，而閥門質量流量等于通過閥內任意完整曲面的流體質量之和，后者和曲面上流體的速度分布相關。因而，閥內速度場分布預測的改變，會影響閥門通流特性預測結果。同時，由相關文獻分析可得知，模型常數a1增加[26]或者β*減少[27]的時候，渦黏度都會相應的增加。原文標定后表3模型常數的變化趨勢和這一點基本上是一致的。綜上所述，模型常數標定的實質是對渦黏度預測的優化。可靠的渦黏度預測可以合理評估閥內湍流摻混作用，準確獲取閥內速度場的分布，這有助于實現高精度的通流特性數值預測。

4 小 結

本文使用數據同化手段，以含濾網蒸汽閥門流動實驗數據為觀測數據，以集合卡爾曼濾波算法為同化算法，重新標定SST模型的常數向量，優化了蒸汽閥門流量特性數值預測的精度。主要結論如下：

1）采用數據同化方法可以有效標定蒸汽調節閥數值模擬的湍流模型常數向量，且標定的常數向量具有可拓展性，可以應用于計算相似開度的其它工況。這對數據同化的工業化應用和蒸汽調節閥通流特性的研究有重要的參考價值。

2）標定的常數向量的可拓展性是有限的。最優模型常數的選擇需要依據閥門開度進行，強行將標定常數用于不同開度下的計算會導致誤差的增加。

3）常數向量可拓展性的限制源于閥內流動形態特征的區別。不同開度下，閥內的流動特征不一致，而不同的流動特征對應不同的最優模型常數向量，因而將特定工況標定的常數向量運用于流動特征相異的工況往往無法實現同樣的效果。

4） 模型常數修正能改變流場內部渦黏度的分布。渦黏度表征湍流對時均流場影響的強弱，從而直接改變閥內速度場的預測，這會對閥門通流特性的預測結果產生影響。

本文的工作是工業化背景下數據同化應用的一次重要嘗試，實現了利用數據同化工具解決工程問題，擴展了數據同化的適用范圍。后續工作可以從數據同化的同化算法入手，即通過對比不同算法對同一工程問題數值模型優化的性能和效率，評估不同算法的優劣，從而評估同化算法對特定工程問題的適用性。