陶瓷基復合材料基體唇形裂紋失效規律研究
李湘萍, 陳 希, 張 鴻, 王小峰
(中國民航大學 中歐航空工程師學院,天津 300300)
1 引 言
陶瓷基復合材料具有重量輕、強度高以及耐高溫、耐腐蝕等優點,是航空發動機和火箭發動機熱端部件的理想材料。在陶瓷基復合材料的制備過程中,基體內部會生成一些缺陷,如裂紋、孔洞和位錯等[1];在受載狀態下,基體開裂也是陶瓷基復合材料最早出現的一種損傷形式。由于陶瓷基復合材料基體為脆性材料,對缺陷或裂紋十分敏感,故其失效機理和失效過程變得更為復雜。
由于基體裂紋的存在,陶瓷基復合材料在使用過程中很容易發生性能退化和失效[2]。建立基體裂紋失效準則是建立陶瓷基復合材料失效模型的基礎,也是研究其細觀損傷演化的前提,很多學者對此開展了研究。脆性基體材料在應力集中處的裂紋萌生是復合材料失效開始的重要判據之一,Henningera等[3]采用內聚力區模型準則預測脆性基體材料中V型裂紋的不穩定擴展;之后為考慮更為復雜的環境條件,Deng等[4]基于能量失效準則,得到了高溫環境下非穩態第一基體開裂應力(FMCS);Farrokhabadi等[5]則采用摩爾-庫倫準則作為基體初始裂紋的判據,從局部失效出發,進一步研究層合板漸進損傷問題。同時,不少學者探究了基體裂紋擴展、裂紋偏轉、裂紋穿透與界面脫粘之間的失效準則問題,如Pompidou[6]基于Cook等[7]的研究結果,分析了陶瓷基復合材料內橢圓形裂紋尖端的應力分布,建立了基體裂紋偏轉的應力失效判據;Parmigiani等[8]以臨界位移為失效標準,結合了強度和韌性參數的內聚力區準則研究了脆性基體材料的基體裂紋在界面處的偏轉判據;更加全面地考慮多種失效機制,Martin等[9,10]通過建立能量釋放率準則研究了基體裂紋向界面擴展、界面脫粘、裂紋偏轉以及裂紋穿過纖維多種失效機制的發生判據;Yan[11]基于正向周應力準則研究了顆粒增強陶瓷基復合材料的裂紋偏轉準則。針對陶瓷基復合材料失效行為的預測,Dassios[12]基于裂紋尖端應力強度因子研究了陶瓷基復合材料的力學行為;Tracy等[13,14]使用J積分和來自數字圖像相關(DIC)的全場變形數據來表征連續纖維陶瓷基復合材料韌性;Gao等[15]以基體應變能準則作為基體損傷準則,分析了加載和卸載過程中纖維滑移區分布,進一步得到了單向纖維增強陶瓷基復合材料的本構關系;Becher等[16]建立了威布爾隨機失效準則來預測CMCs的失效過程;與文獻[16]以基體應變為失效參數標準不同,Higuchi等[17]則基于強度參數,建立威布爾統計強度模型,建立了CMCs失效準則,用于模擬3D編織陶瓷基復合材料失效過程;Zhang等[18]建立了應力強度模型預測基體開裂過程來預測SiC/SiC復合材料的拉伸失效行為,結果表明該模型優于以臨界基體應變能準則建立的模型和以概率統計方法建立的模型;Li[19,20]以基體臨界應變能準則作為基體多裂紋擴展判據,研究了纖維泊松收縮對CMCs基體多裂紋擴展演化的影響,該準則也適用于高溫環境中對基體多裂紋開裂的裂紋密度預測;Skinner等[21]以能量釋放率為基礎,通過應力強度因子與能量釋放率之間的關系,得到了基體裂紋尖端應力強度因子準則,進一步研究了CMCs的損傷演化行為。
以上準則的建立都是針對直線型、三角形或者橢圓形這類規則形裂紋,實際陶瓷基復合材料的基體裂紋要復雜得多。試驗表明[22],陶瓷基復合材料的基體內部存在著中間大兩頭小的曲邊多角形裂紋。很多學者采用唇形裂紋模型來表征這種帶尖角的裂紋[23]。此外,不同于脆性材料,陶瓷基復合材料的基體由于纖維的增韌,表現出一種準脆性的特性,其力學行為具有明顯的非線性[24],這種特性是與裂紋尖端的應力場和位移場密切相關的[25]。本文建立唇形裂紋數學模型,采用復變函數的方法,通過保角映射得到在橫向拉伸載荷下唇形裂紋尖端應力場和位移場的解析解;在此基礎上分別推導了唇形裂紋的應力強度因子準則和最大能量釋放率準則,結合算例分析陶瓷基復合材料唇形裂紋的幾何參數、外載荷以及纖維分布對失效準則的影響規律。
2 唇形裂紋應力場和位移場求解
2.1 建立基體唇形裂紋模型
假設陶瓷基復合材料基體內存在任一唇形裂紋,將陶瓷基復合材料基體看作無限大平面,a為唇形裂紋半長,h為唇形裂紋半寬,唇形裂紋關于x和y軸對稱分布,β=h/a為唇形裂紋的半寬與半長的比值,如圖1所示,本文認為β相同的唇形裂紋具有相同的幾何特征,半長a和半寬h則表示

圖1 受到橫向載荷的唇形裂紋模型
唇形裂紋具有不同的尺寸。假設陶瓷基復合材料受到橫向拉伸載荷的作用,唇形裂紋位于面內并且裂紋邊界是自由邊界,受到無窮遠處沿y軸的均布拉應力σ∞作用。


(1)
在橫向拉伸載荷下,在圖1所示平面內應力σy(x,y)和位移Xy(x,y)的表達式為
(2)
(3)
式中μ=E/2(1+ν),κ=(3-ν)/(1+ν),E為陶瓷基體的彈性模量,ν為泊松比。
假設唇形裂紋邊界用L表示,且在邊界L上不受力,即邊界L上的面力Tx=Ty=0,唇形裂紋邊界的應力邊界條件表示為

(4)


2.2 復勢函數求解

(5)
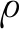

該保角映射將z=x+iy裂紋平面上的唇形裂紋內部映射成了ζ=ξ+iη平面上的單位圓內部,唇形裂紋的邊界映射為單位圓的邊界。并且有w(i)=-a,w(-i)=a,w(1)=hi,w(-1)=-hi。
在受到無窮遠處拉應力σ∞的作用下,自由界面唇形裂紋的復勢函數φ(ζ)和Ψ(ζ)通式可表示為
(6)

取單位圓周上的任一點p,則有p=ei θ,θ為該點幅值。將保角映射Z=w(ζ)代入式(4),并對其取共軛,得到單位圓周上任意點的應力邊界條件為
(7)
(8)

(9)
(10)
為了便于計算,記
(11)
式中

F(ζ)=-J1-J2
(12)
式中J1和J2分別為積分函數的主值,具體表達式為
同樣的方法可以得到J(ζ)的解析解,可表示為
(13)
(14)

同理,也可以得到式(10)的解析解,
(15)

將式(14,15)代入式(6)可得兩個復勢函數的解析解,
(16)
(17)
2.3 唇形裂紋尖端應力場和位移場求解
根據保角映射,式(2)應力場σ(x,y)的表達式可以改寫為
(18)

同理,位移場X(x,y)的表達式也可寫為
(19)
將式(5,16,17)代入式(18,19),可得應力場和位移場關于單位圓平面上映射點的解析解。采用逆映射,即可得到在(x,y)平面內的應力場和位移場σ(x,y)和X(x,y)。
圖3分別給出在橫向載荷σ∞=100 MPa 下,三種不同形狀(β不同)或者不同尺寸(β相同)裂紋尖端應力場和位移場的理論計算與有限元數值模擬的結果對比,其中基體的彈性模量Em=300 GPa,泊松比ν=0.25。有限元計算采用Abaqus中的擴展有限元法實現,有限元模型及其網格劃分結果如圖2所示,上下端面分別施加對稱的均勻分布拉伸載荷σ∞=100 MPa。從圖3可以看出,除了裂紋尖端的奇異性造成的有限元計算結果與理論計算結果相差較大以外,其他部分理論計算結果與有限元計算結果相差不大;此外,當唇形裂紋比較小時,有限元受網格的影響,其計算結果與理論結果有一定偏差。圖3結果證明基于唇形裂紋模型計算得到的應力應變場是有效的。相較于有限元計算方法,本文通過參數化方法更快速地得到了唇形裂紋的橫向拉伸應力應變場,避免了因為劃分網格而造成的計算誤差,既體現了唇形裂紋尖端的應力集中現象,又保持了唇形尖端的應力奇異性。

圖2 唇形裂紋有限元模型

圖3 有限元計算結果與本文計算結果對比(σ∞=100 MPa)
3 唇形基體裂紋失效準則
應力強度因子準則作為裂紋失效的判斷依據是傳統的斷裂力學方法,是更多關注于裂紋尖端的一種局部準則。能量釋放率準則更多地關注于裂紋開裂面,同時考慮了材料性能的作用效果。本文進一步推導出兩種失效準則的表達式。
3.1 應力強度因子準則
裂紋左端點x=a處的應力強度因子定義[28]為
(20)
式中ζ1為裂紋尖端點,即點(a,0)。
將式(5,16)代入式(20),可得唇形裂紋尖端的應力強度因子的表達式
(21)
受到無窮遠處沿y軸均布拉應力σ∞作用的唇形裂紋僅存在I型裂紋擴展,此時,裂紋擴展方向為沿著唇形裂紋尖端的方向,并且當滿足K>KI C,基體裂紋將會發生擴展。
3.2 最大能量釋放率準則
對于脆性材料,通常是在得到裂紋尖端應力強度因子后,通過經驗公式換算得到裂紋尖端能量釋放率[29],優點是不考慮裂紋尖端復雜的應力應變場,便于計算。但是陶瓷基復合材料由于纖維的增韌,基體表現出一種準脆性的特性,這種特性與裂紋尖端的應力應變場密切相關。因此為考慮復雜裂紋造成的裂紋尖端應力應變場變化,在圖1所示y軸拉伸載荷作用下,假設裂紋的初始長度為a,擴展后的裂紋長度為a+Δa,在裂紋擴展的過程中,裂紋擴展段上面力消失的同時,產生了新的張開位移2Xy(x,y),因此勢能Π的變化為

(22)
由此,裂紋尖端最大能量釋放率可表示為
(Δa-x,π)dx
(23)
為簡化計算,將積分改寫為黎曼和的形式,
(24)

由于圖1僅存在I型裂紋擴展,當裂紋尖端的最大能量釋放率滿足G>GI C,基體裂紋將會沿著唇形裂紋尖端的方向失穩擴展。
4 算例分析
以連續纖維增強C/SiC陶瓷基復合材料為例,SiC基體的彈性模量Em=300 GPa,泊松比ν=0.25,C纖維的彈性模量Ef=200 GPa,泊松比ν=0.3,受到如圖1所示橫向載荷的作用。
4.1 幾種模型的比較
圖5分別給出了相同半長的唇形裂紋、Gri-ffith 裂紋和橢圓裂紋計算得到的裂紋尖端應力強度因子K和最大能量釋放率G隨裂紋半長a的變化結果,其中假設唇形裂紋和橢圓裂紋的寬長比β=0.5不變,Griffith裂紋的寬度趨于0,但是長度與唇形裂紋和橢圓裂紋的長度相同。可以看出,基于唇形裂紋計算得到的應力強度因子準則和最大能量釋放率準則的預測規律與Griffith裂紋和橢圓裂紋的預測規律相同,即隨著裂紋半長的增加,三種裂紋的應力強度因子和最大能量釋放率都逐漸增加。在相同半長情況下,唇形裂紋計算得到的應力強度因子和最大能量釋放率都是三種裂紋中最大的。這是因為唇形裂紋在計算裂紋尖端應力強度因子時,能夠考慮裂紋復雜幾何形貌的影響;在計算最大能量釋放率時,還能夠考慮裂紋尖端應力場和應變場的變化情況。因此,基于唇形裂紋的失效準則對裂紋尖端敏感性更高,又考慮到實際陶瓷基復合材料的基體裂紋多為中間大,兩頭小的曲邊多角形,唇形裂紋更適合作為陶瓷基復合材料基體裂紋模型,對唇形裂紋失效準則規律的探究也是十分必要的。

圖5 相同半長的唇形裂紋、Griffith裂紋和橢圓裂紋(β =0.5)
4.2 幾何參數的影響
圖6為基體內存在相同形狀不同大小的唇形裂紋,即寬長比β為定值,半長a或半寬h變化。可以看出,隨著唇形裂紋半長a的增加,半寬h也隨之成比例增加,不同大小唇形裂紋尖端應力強度因子K呈1/2冪指數增加,最大能量釋放率G呈線性增加。說明基體內存在相同形狀的裂紋時,裂紋尺寸越大,依據應力強度因子準則,裂紋越容易起裂,而依據最大能量釋放率準則,裂紋則越容易發生失穩擴展。

圖6 相同形狀不同大小的唇形裂紋
圖7為基體內存在開口寬度相同長度不同的唇形裂紋。即半寬h為定值時,唇形裂紋在受載情況下沿著裂紋尖端的方向發生擴展,半長a不斷增加的情況。可以看出,隨著唇形裂紋半長a的增加,寬長比β不斷降低,唇形裂紋尖端應力強度因子K呈非線性增加,最大能量釋放率G呈線性增加。說明基體開裂后,基體裂紋更容易起裂和失穩擴展。

圖7 開口寬度相同長度不同的唇形裂紋
圖8為基體內存在裂紋長度相同開口寬度不同的唇形裂紋。即半長a為定值時,唇形裂紋在受載情況下產生了變形,半寬h發生變化的情況。可以看出,隨著唇形裂紋半寬h的增加,寬長比β不斷增加,裂紋尖端應力強度因子K和最大能量釋放率G呈較為平緩的增加。說明當基體內存在相同長度的裂紋時,開口寬度越大,越容易起裂和失穩擴展。但是當寬長比β接近1時,即唇形半寬h逐漸等于唇形半長a時,裂紋尖端應力強度因子K和最大能量釋放率G會隨著半寬h的增加而略有下降,從圖9可以看出,裂紋尖端應力強度因子K和最大能量釋放率G在0.8≤β≤1時先增加后下降。根據于靜等[30]的研究,當半寬h大于半長a,即寬長比β>1時,唇形半寬的增加會抑制裂紋的擴展。本文只研究唇形裂紋寬長比β<1的情況。在相同寬長比β情況下,基體裂紋越長,越容易起裂和失穩擴展。
相比于圖6和圖7,半寬h的影響程度要遠小于半長a,即在橫向拉伸載荷下,裂紋變形的影響要小于裂紋擴展的影響。

圖8 長度相同開口寬度不同的唇形裂紋
圖6~圖8表明,對于不同幾何參數的唇形裂紋,裂紋尖端應力強度因子K呈非線性變化,最大能量釋放率G呈線性變化,即采用最大能量釋放率準則的基體裂紋的擴展速率要大于采用應力強度因子準則的。
4.3 外載荷對最大能量釋放率的影響
由式(22),外載荷與裂紋尖端應力強度因子成正比關系;由式(23),外載荷影響了唇形裂紋尖端的應力場和位移場分布,繼而對最大能量釋放率產生了更為復雜的影響。圖10給出唇形裂紋尖端最大能量釋放率隨不同拉應力σ∞的變化曲線。可以看出,對于不同形狀不同大小的唇形裂紋,隨著外載荷的不斷增加,裂紋尖端最大能量釋放率呈拋物線增加,外載荷越大,增加的速率越快。相同外載荷條件下,基體裂紋越長,越容易失穩擴展;基體裂紋變形越大,越容易失穩擴展;基體裂紋尺寸越大,越容易失穩擴展。這也與圖6~圖8的結論一致,符合陶瓷基復合材料基體失效特征。

圖9 長度相同開口寬度不同的唇形裂紋

圖10 不同大小外載荷對唇形裂紋尖端最大能量釋放率的影響
4.4 纖維分布對最大能量釋放率的影響
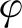

圖11 唇形裂紋尖端和纖維中心距離l和夾角

圖12 纖維分布對唇形裂紋右端點最大能量釋放率的影響
5 結 論
本文建立了橫向拉伸載荷下陶瓷基復合材料基體唇形裂紋模型,采用復變函數的方法并通過保角映射,得到了唇形裂紋尖端的應力場和位移場,在此基礎上推導了唇形裂紋應力強度因子準則和最大能量釋放率準則,得到如下結論。
(1) 裂紋尖端應力場和位移場的解析解與有限元計算結果進行對比,驗證了方法的有效性。
(2) 相較于Griffith裂紋和橢圓裂紋,基于唇形裂紋失效準則的預測規律相同;由于唇形裂紋模型能夠考慮裂紋的復雜幾何形貌和裂紋尖端應力場和位移場的變化情況,基于唇形裂紋的失效準則對裂紋尖端的敏感性更高,更適于預測具有曲邊多角形裂紋的陶瓷基體裂紋的擴展。
(3) 對于不同幾何參數的唇形裂紋,采用最大能量釋放率準則的基體裂紋的擴展速率要大于應力強度因子準則的。
(4) 相同外載荷條件下,基體裂紋越長,越容易發生起裂和失穩擴展;基體裂紋變形越大,越容易發生起裂和失穩擴展;基體裂紋尺寸越大,越容易發生起裂和失穩擴展;裂紋長軸位于纖維的中心線上而且最接近纖維中心的唇形裂紋最容易發生失穩擴展,符合陶瓷基復合材料基體失效特征。

