覆水飽和雙相介質圓弧場地P波激勵下散射問題的理論解

柳國環， 黃偉緯， 李鑫洋

(天津大學 建筑工程學院，天津 300350)

1 引 言

當前國內水域環境下長大工程日趨增多，如翔安海底隧道(海域段長4.2 km)和港珠澳大橋海底隧道(海域段長5.6 km)等。長大結構地震反應分析的科學性依賴于地震動輸入的合理性，地震動輸入的合理性又直接體現在場地因素對地震動的影響。對于水域長大結構抗震研究，需要考慮地震動輸入在不同位置的差異性，即空間變異性[1]。因此，準確反映場地特性的空間相關多點地震動場對水域長大結構的地震響應分析至關重要。

關于場地因素的地震動場研究，Trifunac等[2-4]率先采用Fourier-Bessel級數展開法研究SH波在圓弧狀峽谷和沉積河谷地下的散射。袁曉銘等[5]給出了圓弧形凹陷地形對平面SH波散射問題的級數解答。Cao等[6,7]采用波勢函數展開法得到了P波和SV波入射凹陷地形的波函數解析解；梁建文等[8,9]研究了P波和SV波入射圓弧形沉積谷場地下的動力響應。此后，眾多國內外學者[10-13]對更加復雜地形的地震波場做了進一步的研究。柳國環[14,15]研究了SH波入射非均勻介質V形和圓弧形峽谷的多點地震動模擬方法，引入第二類分層效應，并開發了相應的多點地震動模擬程序。該研究在本質上考慮的是單相介質地震波場，并不完全適合水域長大結構的抗震研究，但為更加復雜覆水場地地震動理論研究奠定了基礎。對覆水場地地震動模型進行研究，需要在單相介質地震動研究的基礎上引入Biot理論[16]，并考慮場地非平坦效應。李偉華等[17,18]基于飽和圓弧凹陷地形給出了P波和SV波的地表位移解析解。Liu等[19-21]提出一種有效的模擬地震地下運動的方法，并針對無覆水以及覆水飽和多層場地生成了地下多點地震動模型。目前，現有研究成果對于更加復雜水域地形(同時考慮覆水層、雙相介質、分層效應和非平坦等場地特性)地震波場的討論還比較少。

為了給復雜水域地形環境下的長大結構提供科學合理的地震動輸入，本文研究了P波入射覆水飽和雙相介質圓弧場地地震響應的理論解。研究的基本思路為，(1) 在直角坐標系下推導并得到覆水多層平坦場地的地震波場分布，并用Fourier-Beseel級數展開為自由波場； (2) 在極坐標系下采用波函數展開法，代入邊界條件，求解含有待定系數的散射波場； (3) 通過自由波場和散射波場得到場地地表位移幅值分布。研究旨在為復雜水域地形環境下長大結構的抗震分析提供理論基礎。

2 場地模型與基本理論

2.1 覆水飽和雙相介質圓弧場地模型

場地模型如圖1所示，在圓弧場地的圓心處建立平面直角坐標系。一列圓頻率為ω，入射角為α1d的P波由底部入射覆水飽和雙相介質圓弧場地，入射波的勢函數Ψi(x,y)表示為

Ψi=ei (ω t -k1d x sin α1d+k1d y cos α1d)

(1)

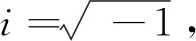
本文場地模型的最上層為覆水層，中間的u層和底部的d層均為彈性和各向同性且均勻的飽和土層(雙相介質)。

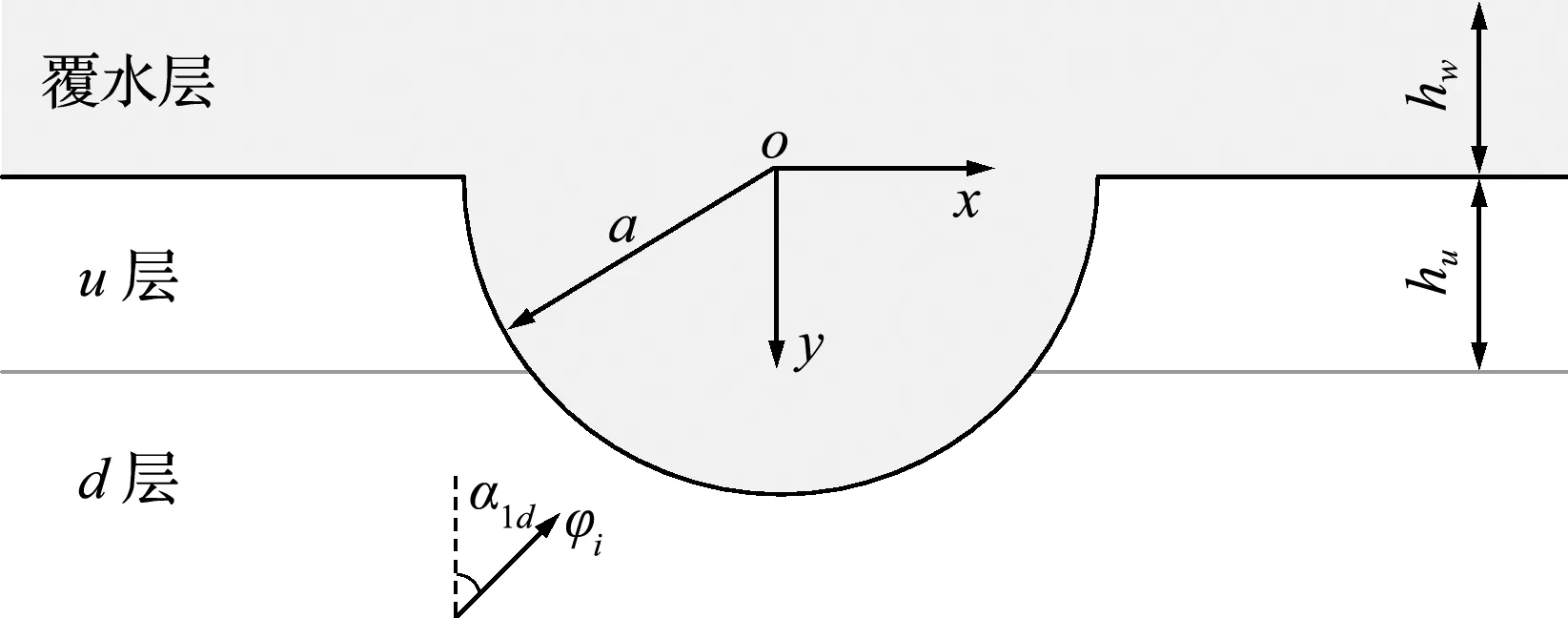
圖1 覆水飽和雙相介質圓弧場地

2.2 飽和雙相介質波動方程基本理論

依據Biot多孔介質波動理論[15]，雙相介質波動方程可以表示為

(2)

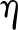
飽和雙相介質中的波勢函數表示為

(n=1，2)(3)

式(2,3)的波數和波速通過式(4)計算得到，

(4)

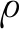
雙相介質中位移和應力分別表示為

(5)

(6)

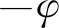
σi j=(Ae+Qξ)δi j+2Nei j

(7)

式中x表示水平方向，y表示豎直方向，σi j為應力，δi j為Kronecker系數，當i=j時，δi j=1，否則δi j=0，e=·u,ξ=·U，為孔隙水壓力，β為液相勢函數和固相函數的比值，下標1，2和3分別代表P1波、P2波和SV波，其可通過文獻[21]計算求得。

覆水層中P波的波勢函數可以表示為

Fwei (ω t -kp wx sinαp w -kp wy cosαp w)

(8)

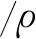
覆水層中的位移和應力表示為

(9)

2.3 覆水場地邊界條件

場地存在三種邊界面，分別是土-水分界面、飽和土層分界面和覆水層表面。

(1) 土-水分界面上，滿足應力和位移連續條件

(ux)u=(Ux)w, (uy)u=(Uy)w

(σy y+τ)u=(-p)w, (σx y)u=0

(10)

(2) 在飽和土層之間的分界面上，除滿足應力和位移連續外，還滿足孔隙水壓和流量連續。

(ux)u=(ux)d, (uy)u=(uy)d

(σy y+τ)u=(σy y+τ)d

(σx y)u=(σx y)d，pu=pd

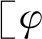
(11)

(3) 在覆水層自由表面處壓力為0,即

(12)

3 場地波場分布及求解

復雜場地波函數的求解需要分為兩個步驟，首先求解自由波場，其次求解散射波場。

3.1 自由波場

假定覆水場地中不存在圓弧地形，則P1波自下而上入射覆水分層介質場地，在飽和土層分界面處發生反射和透射現象，產生反射P1波、P2波和SV波，以及透射P1波、P2波和SV波。波函數分別為

(13)

將式(13)代入邊界條件(11)，經簡化得

S=TH

(14)

式中H=[F1dF2dF3dE1uE2uE3u]，T和S分別為6×6階和6×1階矩陣(篇幅所限，本文略去矩陣具體形式)。

通過求解方程(14)獲得P1波入射飽和土層分界面的反射和透射系數，即得到勢函數的幅值系數F1d，F2d，F3d，E1u，E2u和E3u。

在飽和土u層中，下行波勢函數表示為

(15)

其中

(16)

式中rm n為反射系數，m和n代表入射波和反射波，如rP 1P 2為當P1波入射土-水分界面時P2波的反射系數。

覆水層中的上下行波勢函數可以表示為

(17)

其中

(18)

式中tm為透射系數，m為入射波，如tP 1為當P1波入射土-水分界面時P1波的透射系數。

上述土-水分界面的反射和透射系數可以通過邊界條件(10)確定，得到

I|n=DR|n

(19)

式中下標n表示P1波、P2波或SV波，如當入射波為P1波時，R|P 1=[rP 1P 1rP 1P 2rP 1S VtP 1],D和I分別為4×4階和4×1階矩陣。

解方程組(19)，獲得P1波入射土-水分界面的反射和透射系數。同理，可獲得P2波以及SV波入射土-水分界面的反射和透射系數，進而得到所有土層以及覆水層上行和下行波函數的幅值系數。

為了便于求解，將上述自由波場勢函數轉換到極坐標系中，具體方法可參考文獻[6]。

3.2 散射波場

研究P波入射覆水飽和雙相介質圓弧場地散射波場分布時，需要考慮地震波在圓弧場地邊界產生散射P1波、P2波和SV波，在(r,θ)坐標系中，波函數分別為

為了便于求解，分別采用一個半徑很大的大圓弧替代水平自由表面、土-水分界面和飽和土層分界面。當大圓弧的半徑足夠大時，大圓弧邊界就可以近似看成是水平界面，如圖2所示。

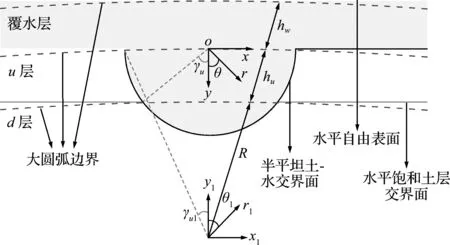
圖2 考慮大圓弧邊界的場地示意圖

在(r1,θ1)坐標系中，大圓弧邊界的存在產生了散射波場，波函數分別為

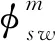
上述由圓弧地形及考慮大圓弧近似假定給出的波函數分別在(r,θ)和(r1,θ1)坐標系給出，為了使波函數轉換在同一坐標系下，Graf加法變換公式將(r1,θ1)坐標系中圓弧地形邊界產生的散射波場函數轉換到(r,θ)坐標系中；同樣，把(r1,θ1)坐標系中的大圓弧邊界產生的散射波場函數轉換到(r,θ)坐標系中。經過上述轉化，能夠在同一坐標系中對波函數進行運算。

3.3 總波場分布

通過上述推導及坐標變換，能夠獲得覆水飽和雙相介質圓弧場地的總波場分布。覆水層中的標量勢函數表示為

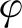
(20)

飽和土u層中固相和液相的標量勢函數，以及固相和液相的矢量勢函數分別表示為

(21)

同理，飽和土d層中的固相和液相的標量勢函數，以及固相和液相的矢量勢函數分別表示為

(22)

3.4 波函數未知系數求解

散射波場波勢函數含有未知系數，求解波場分布的關鍵就在于求解未知系數。篇幅有限，故略去中間推導過程，以流程圖的形式給出散射波場的求解流程，如圖3所示。結合本章前3節的內容，將波函數代入邊界條件，求出未知系數，最終得出波場函數頻域解。

4 驗證及分析

4.1 可靠性驗證

為了便于分析，先定義無量綱頻率

(23)

采用峽谷寬度和入射波波長的比值來間接描述入射波的頻率。同時，考慮到數值計算時，大圓弧半徑過大會導致貝塞爾函數值過小，矩陣出現奇異性，導致計算溢出。故本文假定大圓弧半徑為

R=100a

(24)

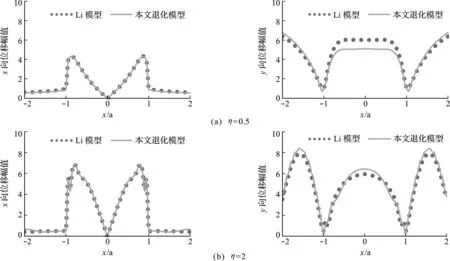
為了說明理論推導的正確性，本文模型與Li模型做了對比。 Li模型具有圓弧凹陷地形和飽和介質場地的特點，而本文模型具有半圓弧凹陷地形、覆水層和飽和雙相介質綜合屬性。因此，設置覆水層的高度為0，并將兩層介質物理參數設置一致，同時設置Li模型的參數，將其圓弧凹陷地形設置成半圓弧凹陷地形，則本文模型可以退化成Li模型。本文退化模型和Li模型在P波入射下的算例對比情況如圖4所示。結果表明，不論是低頻入射還是高頻入射，對于x方向位移幅值，本文退化模型和Li模型顯示出了較高的吻合度；對于y方向，兩模型之間的位移幅值也具有良好的一致性，進一步證明了理論推導的正確性。

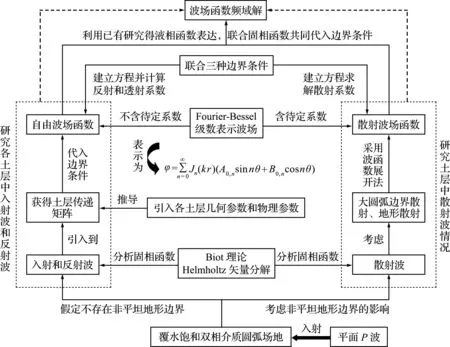
圖3 圓弧場地波場求解流程

4.2 地表位移分析

進一步分析入射角和入射波頻率對場地地表位移的影響。

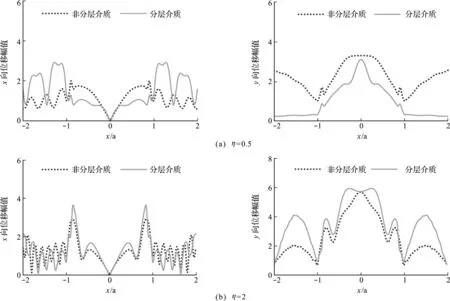
圖5給出了P波垂直入射(θ=0°)覆水場地時，分層介質與非分層介質地表位移的對比情況。結果表明，P波垂直入射峽谷場地時，分層介質的地表位移和非分層介質的地表位移有著顯著的區別。不論在x方向還是y方向，分層介質與非分層介質的地表位移幅值相比會放大或縮小一定值，從而使得分層介質場地地表位移波動變得更加劇烈。這是由于入射P波在飽和分層介質分界面發生波形轉化現象，衍生的P1，P2和SV波與峽谷非平坦表面產生的散射波互相影響，使得空間波場分布更加復雜，這些復雜平面波之間彼此產生干涉現象，在峽谷表面的某處產生位移的疊加或相消，使得分層介質的地表位移幅值高于或者低于非分層介質。同時可以發現，分層與非分層介質在峽谷兩側x和y方向的地表位移均具有良好的對稱性，且在峽谷中心點x方向的位移幅值為0。這種現象是由于P波垂直入射峽谷分層介質分界面時，并未產生耦合的SV波，從而只有垂直方向的運動；同時,在峽谷邊界的散射波也由于地形的對稱性，使水平方向的位移相互抵消，最終導致峽谷底部中心點的水平方向位移為0，且峽谷兩側地面運動呈現出對稱性。

圖6給出了更加常見情況下的位移幅值對比,即P波斜入射(θ=30°)覆水圓弧場地時，分層介質與非分層介質地表位移幅值的對比。與垂直入射相比，斜入射P波的峽谷兩側地表位移不再具有對稱性。對比圖5可以看出，不論波是垂直入射還是斜入射，分層介質會明顯地改變地表的震動特性。震動特性改變程度一方面受分層介質物理性質的影響,兩層介質物理性質差異越大，其與單層介質的地表位移差異也就越大；另一方面，受到入射波特性的影響,入射波頻率和角度等指標不同，會改變場地波場的分布，進而發生不同的干涉現象，從而使得地震地面運動幅度發生較大的變化。

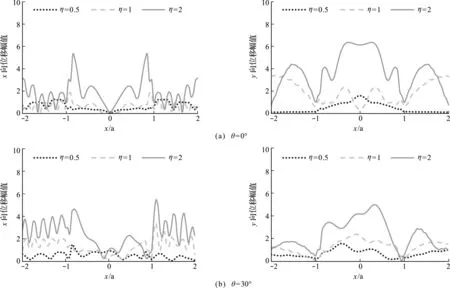
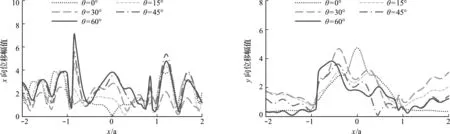
為了進一步說明入射頻率和入射角度等對地震地面運動特性的影響，圖7給出了分層介質情況下，入射波頻率和地表位移的關系。結果表明，隨著入射波頻率的增大，地表位移幅值也逐漸增加，并且地表位移的波動性也隨之增加。入射波頻率增加意味著能量增加，所以高頻波地表位移幅值明顯大于低頻波地表位移幅值。此外，當入射波頻率較低時，x和y方向的地表位移幅值均較小，波動也較小。隨著入射波頻率增大，波對場地介質的不均勻性(分層特性)變得較為敏感，使得位移幅值顯著增加，峽谷不同點的位移差，即波動性也增加。特別如圖7(b)所示，當P波從峽谷底部左側向峽谷右側斜入射時，峽谷左側直接受到入射波作用，因而左側圓弧地表(-1≤x/a≤0)的位移均明顯大于峽谷右側圓弧地表(0

表1 飽和土的物理參數Tab.1 Physical parameters of saturated soil

圖4 本文退化模型與Li模型對比情況

圖5～圖7表明，地震波垂直入射和斜入射覆水場地時，會對地震地面運動產生不同影響。圖8給出了分層介質情況下，不同入射角對地表位移幅值的影響,進一步證明了無論入射角如何變化，P波從峽谷底部左側向右側斜入射時，峽谷左側圓弧地表由于受到地震波的直接作用，故其左側圓弧地表位移幅值大于右側。縱觀整個峽谷地表場地，當入射角較大時，峽谷地表的水平方向位移幅值也較大；而對于豎直方向的峽谷地表位移，入射角度較大的豎直地表位移幅值反而較小。出現這種現象的原因是，在入射波總能量一定時，隨著P波入射角度的增加，其質點的振動方向從只有豎直振動向同時有豎直和水平振動轉變，使得水平振動所分配的能量逐漸增加，豎直振動所分配的能量相對減少。無論是水平方向還是豎直方向，入射角的改變對位移幅值的最大值和最小值的影響并不顯著，但是其對地震地面運動分布特性影響較大，因而不能忽略入射角對地面運動的影響。

圖5 垂直入射下(θ =0°)分層與非分層介質對地面運動的影響

圖6 斜入射下(θ =30°)分層與非分層介質對地面運動的影響

圖7 場地分層情況下入射頻率對地表位移的影響

圖8 場地分層情況下 =0.5)入射角對地表位移的影響

5 結 論

本文率先針對具有覆水層、飽和雙相介質、非平坦以及第二類分層(場地跨越分層界面)等復雜特征場域在壓縮波入射下的地震反應進行研究。主要工作包括:

(1) 推導并得到了覆水圓弧飽和雙相介質場地的自由波場。引入覆水層對雙相飽和介質場地的影響，推導出地震波在飽和土層分界面和土-水分界面的反射和透射系數；確定了每一層介質中的上行波和下行波，得到覆水圓弧飽和雙相介質場地的地震波自由場。

(2) 推導并得到了覆水圓弧飽和雙相介質場地的散射波場。引入非平坦特性對場地波場的影響，獲得場地的所有波場分布；利用場地邊界條件，嚴格按照數學推導得到待定系數的值。

(3) 得到并分析了場地的地表位移。得到覆水圓弧飽和雙相介質場地的地表位移；通過和其他算例對比，驗證了理論推導的可靠性；分析了場地分層介質和非分層介質的地震地面運動特性以及不同入射頻率和入射角對地震地面運動特性的影響，結果表明，分層介質有著與非分層介質完全不同的波場分布，會顯著改變地震地面運動特性，因此必須考慮分層效應對波場的影響；入射波頻率的增大會明顯提升地震地面運動幅值，并加強其波動性，同時入射角的改變對地震地面運動特性也有較大影響。