轉動副間隙對精密機構非線性動力學影響分析

陳宇 奚圣賢 邱睿 肖宇婷

摘要：為了深入研究含間隙轉動副機構的動態特性，基于多體動力學理論、Hertz接觸理論和庫倫摩擦理論，提出一種含間隙機構動力學建模方法。將多體系統動力學方程與非線性接觸碰撞模型相結合，并考慮碰撞體之間的切向摩擦作用，建立了含間隙多體系統的非線性動力學模型。在重力場作用下對不同非線性接觸碰撞過程進行仿真計算，并詳細討論了模型參數對接觸碰撞過程的影響，在此基礎上，對間隙與機構動態特性響應關系進行比較和分析。研究表明，含間隙非線性碰撞多體動力學模型能夠有效地描述含間隙機構的動態特性，在工程實際應用中，有利于進行機構的性能評價、結構設計優化等。

關鍵詞：轉動副間隙;連續碰撞;能量損失;動態特性

中圖分類號：TH122文獻標識碼：A文章編號：2095-7394（2021）06-0067-12

現代工業發展的趨勢是高精度、高可靠、高壽命，這對大力發展能夠廣泛用于復雜工況的精密機構提出了更高要求[1-2]。轉動副是精密機構重要的組成部分，而轉動副間隙會造成軸與軸承之間發生接觸、碰撞以及磨損，這必定會引起機構產生振動現象，進而影響精密機構的運動精度[3-4];因此，建立轉動副間隙特征，并分析其對精密機構的動態特性影響具有重要意義。

當前，國內外學者針對含間隙機構動力學建模與分析問題進行了大量研究，例如：白爭鋒等人[5]考慮轉動副連續接觸碰撞特征，提出了一種非線性接觸碰撞模型，較好地描述了接觸碰撞時的變形量，并基于該模型建立了含間隙多體系統的動力學模型;李媛媛等人[6]考慮桿件柔性特征，建立了含間隙機構剛柔耦合分析模型，并詳細分析了間隙尺寸及數量對機構動力學特征的影響;Erkaya等人[7]采用理論分析與試驗相結合的方式，研究了不同工況下含間隙多體系統振動特征;考慮能量損失的影響，俞成濤等人[8]基于多體動力學方法，研究了間隙特征對轉動副動力學性能的影響。

然而，上述含間隙精密機構動態特征研究一般僅限于連續接觸的假設條件，很少考慮轉動副元素運動狀態之間的轉變（分離、接觸、變形）;因此，本文基于多體動力學理論、Hertz接觸理論和庫倫摩擦理論，建立了一種含間隙非線性碰撞的精密機構動力學模型。在此基礎上，以典型曲柄滑塊機構在重力場中的接觸碰撞過程為對象，進行了動力學仿真計算，并針對間隙與機構之間的動態特性響應關系，做出詳細分析。

1含間隙機構動力學建模

1.1含間隙轉動副運動學建模

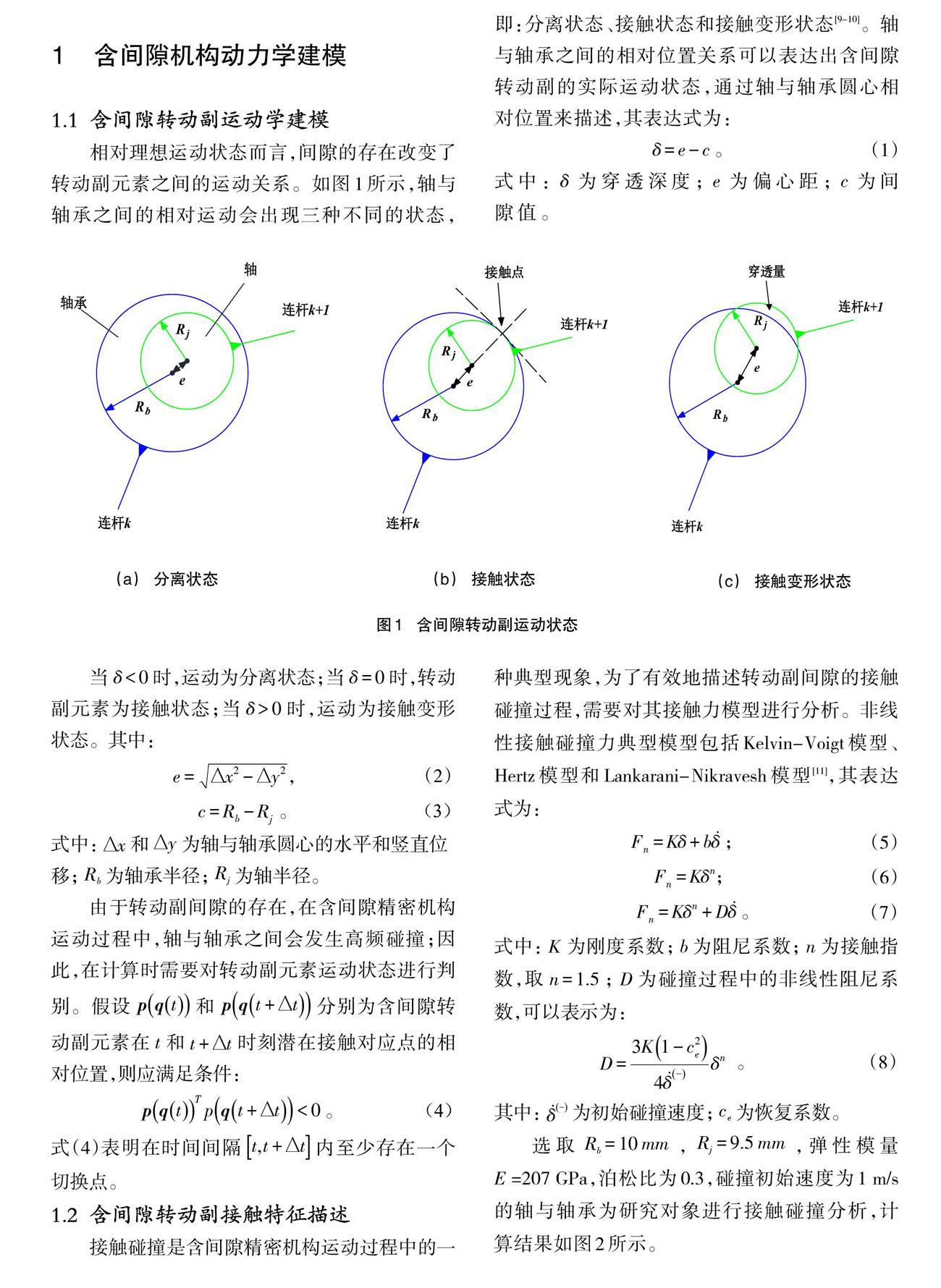
相對理想運動狀態而言，間隙的存在改變了轉動副元素之間的運動關系。如圖1所示，軸與軸承之間的相對運動會出現三種不同的狀態，即：分離狀態、接觸狀態和接觸變形狀態[9-10]。軸與軸承之間的相對位置關系可以表達出含間隙轉動副的實際運動狀態，通過軸與軸承圓心相對位置來描述，其表達式為：

δ=e-c。（1）

式中：δ為穿透深度;e為偏心距;c為間隙值。

當δ<0時，運動為分離狀態;當δ=0時，轉動副元素為接觸狀態;當δ>0時，運動為接觸變形狀態。其中：

式中：Δx和Δy為軸與軸承圓心的水平和豎直位移;R_b為軸承半徑;R_j為軸半徑。

由于轉動副間隙的存在，在含間隙精密機構運動過程中，軸與軸承之間會發生高頻碰撞;因此，在計算時需要對轉動副元素運動狀態進行判別。假設p（q（t））和p（q（t+Δt））分別為含間隙轉動副元素在t和t+Δt時刻潛在接觸對應點的相對位置，則應滿足條件：

p（q（t））^Tp（q（t+Δt））<0。（4）

式（4）表明在時間間隔[t，t+Δt]內至少存在一個切換點。

1.2含間隙轉動副接觸特征描述

接觸碰撞是含間隙精密機構運動過程中的一種典型現象，為了有效地描述轉動副間隙的接觸碰撞過程，需要對其接觸力模型進行分析。非線性接觸碰撞力典型模型包括Kelvin-Voigt模型、Hertz模型和Lankarani-Nikravesh模型[11]，其表達式為：

式中：K為剛度系數;b為阻尼系數;n為接觸指數，取n=1.5;D為碰撞過程中的非線性阻尼系數，可以表示為：

選取R_b=10 mm，R_j=9.5 mm，彈性模量E=207 GPa，泊松比為0.3，碰撞初始速度為1 m/s的軸與軸承為研究對象進行接觸碰撞分析，計算結果如圖2所示。

對比計算結果可知：Kelvin-Voigt模型計算簡單方便，但存在一定的局限性，接觸碰撞力在初始接觸時不連續，相對速度可能會出現負值;Hertz模型可以描述接觸力和變形量之間的非線性關系特性，但其結果表明在接觸碰撞過程中接觸能量與恢復能量相等，則無法表示接觸碰撞過程中的能量損失特征;相對其他接觸碰撞力模型而言，Lankarani-Nikravesh模型不僅能夠描述接觸碰撞過程中的能量損耗情況，而且還能反映阻尼滯后的特性，從而更能接近實際地表達轉動副間隙的接觸碰撞過程。因此，本文以Lankarani- Nikravesh模型為基礎，建立含間隙精密機構動力學模型。

摩擦力也是含間隙轉動副接觸碰撞過程中重要的參數之一，可表示接觸時切向力的力學特征。為了準確地描述轉動副元素接觸碰撞過程中的粘滯微滑特性，本文基于Coulomb修正模型，描述摩擦力與切向滑動之間的關聯特性[12]，其表達式為：

式中：c_f表示滑動摩擦系數;v_t為接觸單元切向速度;c_d為動態摩擦系數，

其中，v₀和v₁為給定的速度極限值。

1.3含間隙機構動力學建模

基于上述分析可知，含間隙機構動力學分析的關鍵在于多體系統不同運動狀態的轉變，本文采用運動分段的建模方法來進行含間隙機構動力學性能的計算。在分離運動狀態時，軸承與軸處于分離狀態，不含間隙轉動副單元處的幾何約束依然存在[13]。根據拉格朗日乘子法，其動力學方程為：

式中：M、C和K分別為系統的廣義質量陣、阻尼陣和剛度陣;q表示廣義坐標矩陣;φ_q為廣義約束方程φ（q，t）=0的雅克比矩陣;λ和f分別表示廣義力陣和Lagrange乘子列陣。

當軸與軸承發生接觸碰撞時，轉動副元素之間增加的等效接觸碰撞力其系統動力學表達式可寫為：

式中，F_c為接觸力相對于廣義坐標q的廣義力列陣，即：F_c=F_n+F_t。

2非線性接觸碰撞力模型分析

轉動副間隙是影響機構運動軌跡的重要因素，而接觸碰撞力模型的描述是判斷機構動力學分析準確性的重要指標，本文基于Lankarani-Nikravesh模型，詳細分析模型參數對接觸碰撞過程的影響。

2.1間隙尺寸影響分析

含間隙轉動副基本計算條件與前述相同，針對一次碰撞過程進行分析，間隙尺寸分別取0.01 mm，0.10 mm，0.50 mm，1.00 mm，恢復系數為0.9，計算結果如圖3所示。由計算結果可知：隨著間隙尺寸的變化，接觸力、變形量和變形速度都發生了明顯的改變，產生這種現象的原因是間隙尺寸的改變會引起接觸剛度的變化，從而影響轉動副元素的接觸碰撞過程;同時，隨著間隙尺寸的增大，阻尼滯后現象非常明顯，但間隙尺寸的變化對接觸碰撞過程中的能量損失幾乎沒有影響。

2.2恢復系數影響分析

恢復系數是改變含間隙轉動副運動過程的重要元素之一，為了進一步深入研究含間隙轉動副接觸碰撞過程，本文進行不同恢復系數c_e（0.5，0.7，0.9，1）對接觸碰撞過程的影響分析，計算結果如圖4所示。

由計算結果可知，隨著恢復系數的增加，接觸力和變形量明顯增大。雖然接觸碰撞的時間有所減小，但達到最大變形量的時間卻有所增加，這是由于恢復系數的增加會促使接觸碰撞中恢復過程加快。此外，恢復系數的增加會引起碰撞阻尼力的減少，從而加大接觸碰撞過程中能量的損耗。

2.3初始碰撞速度影響分析

為了更好地研究含間隙轉動副非線性接觸碰撞過程，將不同初始碰撞速度v₀（1m/s，3 m/s，5 m/s，10 m/s）代人到計算模型中，計算結果如圖5所示。由計算結果可知：初始碰撞速度的增加會引起接觸力和變形量的增大，當初始碰撞速度為1 m/s時，最大接觸力為2.321 9×10⁴N，最大變形量為4.950 8×10^-5m;當初始碰撞速度增大到10 m/s時，最大接觸力為2.418 9×10⁴N，而最大變形量為5.116 8×10^-5m。除此之外，初始碰撞速度的增加會加快含間隙轉動副的接觸碰撞過程，降低其過程的能量損耗。

3含間隙機構動態特性分析

如圖6所示，本文采用曲柄滑塊機構作為分析對象來研究含間隙精密機構動力學行為特征。該機構包含曲柄、連桿、滑塊三個主要部件，其幾何參數為：R=0.165 m，L=0.38 m，c_e=0.9，E=210 GPa，曲柄質量0.3 kg，連桿質量0.21 kg，滑塊質量0.148 kg，摩擦系數0.03。轉動副間隙存在于連桿與滑塊連接處。根據前述數學模型表達式，將已知參數代人到式（1）至式（12）中，并采用Runge-Kutta對其方程進行求解。

3.1轉速對機構動態特性的影響

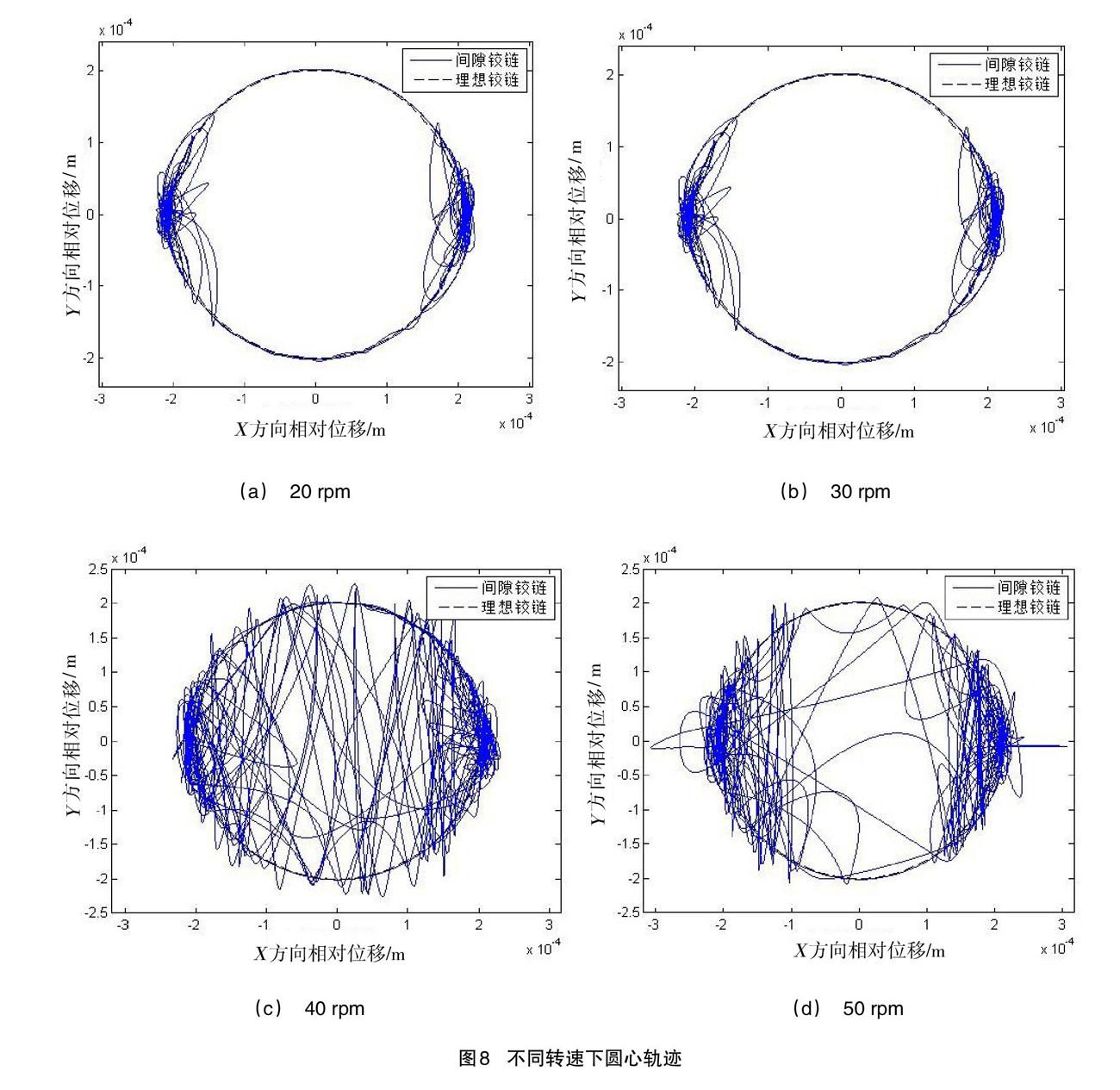
圖7和圖8研究了在間隙尺寸為0.2 mm時，轉速（20 rpm，30 rpm，40 rpm，50 rpm）對機構動態特性的影響，從計算結果可以發現：（1）轉速的增加對滑塊位移影響較小，但隨著轉速的增加，滑塊速度與加速度軌跡增幅較大，且加速度曲線出現明顯的振動現象，轉速越高振動現象越明顯。產生該現象是由于隨著機構運行速度的提高，會引起含間隙轉動副接觸碰撞頻率和接觸碰撞速度的增加，從而引起機構產生較大的振動。（2）相比位移和速度結果來說，加速度曲線對機構振動現象反映更加明顯，可以更好地顯示機構振動現象。（3）從圓心運動軌跡可以看出含間隙轉動副在運動過程中的狀態變化，在低轉速時主要以接觸運動為主，圓心運動軌跡貼近理想曲線。隨著轉速的增加，碰撞頻率、運動狀態明顯發生變化，且在50 rpm時出現較大的變形量。

3.2間隙尺寸對機構動態特性的影響

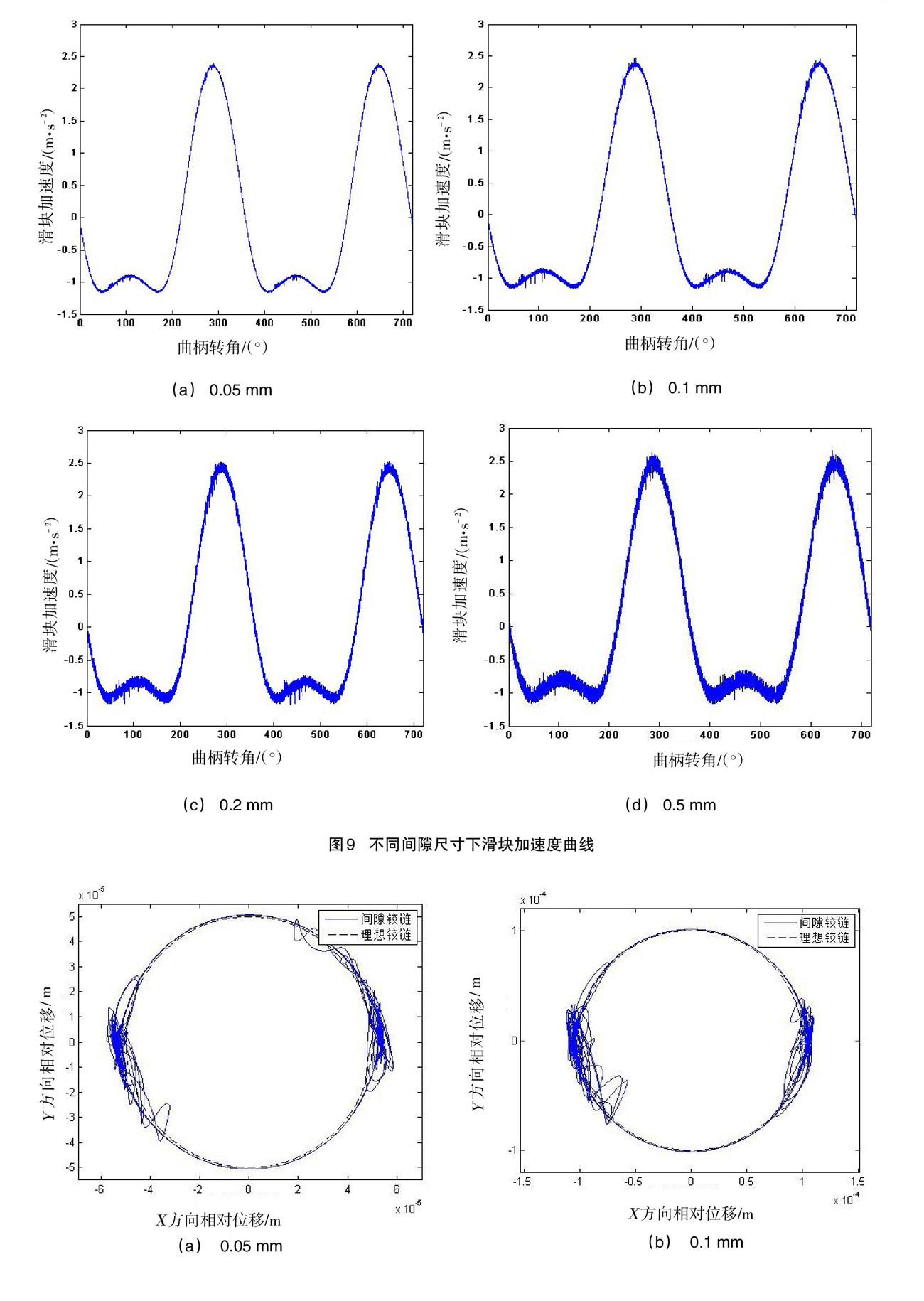
圖9給出了不同間隙尺寸（0.05 mm，0.1mm，0.2 mm，0.5 mm）下，當轉速為40 rpm時的滑塊加速度變化曲線。從計算結果可以發現：隨著間隙尺寸的增加，滑塊加速度振動逐漸增大，尤其是在極限位置區域時滑塊產生較大的振動現象，但滑塊加速度極值并未產生較大的波動。這是由于間隙尺寸的增加促使接觸力和變形量明顯增大，這將會引起含間隙轉動副圓心距的增加，從而增大機構的振動效應。

如圖10所示為不同間隙尺寸下圓心軌跡，可以看出：不同間隙尺寸下轉動副元素均會產生分離狀態、接觸狀態、接觸變形狀態三種特征，但每種狀態所在周期并不相同;隨著間隙尺寸的增加，碰撞頻率、變形量都有所增加，尤其是當間隙尺寸達到0.2 mm以后，穿透深度明顯增強，這將會引起機構運動的不穩定，甚至發生混沌和分岔現象。

4結論

基于多體動力學理論、Hertz接觸理論和庫倫摩擦理論，本文提出一種含間隙非線性的多體動力學建模方法。基于該方法，以含間隙精密機構為對象，進行了動態特性響應分析。研究結果表明：

（1）間隙尺寸、恢復系數、初始碰撞速度對含間隙轉動副接觸碰撞過程均會產生明顯的影響，特別是間隙尺寸的改變會引起明顯的阻尼滯后現象。

（2）從動件加速度對轉速增加較敏感，隨轉速的增加，轉動副的碰撞力增加，出現高頻振蕩等特點，對機構的運動精度影響較大。

（3）本文建立的含間隙非線性柔性碰撞多體動力學模型，能夠較好地描述機構運動的動態特性，為機構動態特性研究提供了一種有效的方法。

參考文獻：

[1]王尚斌，孫宇，彭斌彬.曲柄滑塊機構轉速波動與動態靜力綜合分析[J].華中科技大學學報（自然科學版），2014，42（1）：28-33.

[2]俞成濤，劉聰，徐龍祥.三支承磁懸浮軸承的不對中特性[J].機械設計與研究，2018，34（3）：94-99.

[3]聶飛飛，周金宇，曹清林.高速經編機槽針機構運動精度可靠性優化[J].機械設計與制造，2019，12（12）：40-44.

[4]陳修龍，陳天祥，李躍文，等.3-PRR并聯機器人機構運動學建模與分析[J].山東科技大學學報（自然科學版），2018，37（5）：79-87.

[5] BAI Z F，ZHAO Y.Dynamicbehaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model[J]. International Journal of Mechanical Science，2012，54（1）：190-205.

[6] LI Y Y，WANG Z L，WANG C，et al. Planar rigid-flexible coupling spacecraft modeling and control considering solar array deployment and joint clearance[J]. Acta Astronautica，2018，142：138-151.

[7] ERKAYA S，UZMAY I. Effects of balancing and link flexibility on dynamics of a planar mechanism having joint clearance [J]. Scientia Iranica，2012，19（3）：483-490.

[8] YU C T，ZHU Y，SHI F，et al. Modeling and experimental validation of transient response of magnetic suspension rotor contacting with auto- reducing clearance auxiliary bearing [J]. Journal of Sound and Vibration，2020，481：115419.

[9]郭嘉楠，何鵬，劉占生，等.粗糙接觸面旋轉鉸間隙碰撞動力學建模與仿真[J].振動與沖擊，2019，38（11）：132-139.

[10]李發家，朱如鵬，靳廣虎，等.多間隙高重合度齒輪傳動系統動力學分岔與穩定性分析[J].華南理工大學學報（自然科學版），2015，43（6）：63-69.

[11]鄭延豐，楊超，劉磊，等.基于有限質點法的含間隙鉸平面機構動力分析[J].工程力學，2020，37（3）：8-17.

[12]趙波，戴旭東，張執南，等.柔性對多體系統中鉸接副磨損的影響[J].摩擦學學報，2014，33（6）：705-714.

[13] TIAN Q，LOU J，MIKKOLA A. A new elastohydrodynamic lubricated spherical joint model for rigid-flexible multibody dynamics[J]. Mechanism and Machine Theory，2017，107：210-228.

Analysis of the Influence of Revolute Clearance Joint on Nonlinear Dynamics of Precision Mechanism

CHEN Yu，XI Shengxian，QIU Rui，XIAO Yuting

（School of Mechanical Engineering，Jiangsu University of Technology，Changzhou 213001，China）

Abstract：In order to investigate the dynamic characteristics of revolute joint mechanism with clearance in detail，a dynamic modeling method of mechanism with clearance is proposed based on multi-body dynamics theory，Hertz contact theory and Coulomb friction theory. The nonlinear dynamic model of multi-body system with clearance is established by combining the dynamic equation of multi-body system with nonlinear contact collision model and considering the tangential friction between collision bodies. The different nonlinear contact collision processes are simulated under the action of gravity field，and the influence of model parameters on the contact collision process is detailedly discussed. On this basis，the response relationship between clearance and dynamic characteristics of mechanism is compared and detailedly analyzed. The research shows that the multi- body dynamics model of nonlinear collision with clearance can effectively describe the dynamic characteristics of the mechanism with clearance，which is conducive to the performance evaluation and structural design optimization in practical application of engineering.

Key words：revolute clearance joint;continuous contact;energy loss;dynamic characteristic