基于AHP聚類分析的中國區域經濟協調發展評價

李娜

(榆林學院 政法學院， 陜西 榆林 719000)

0 引言

改革開放三十年,伴隨著中國經濟增速不斷穩步提高，社會、生活和環境等多方面均發生了翻天覆地的變化。同時，地區發展不均衡，經濟發展差異也尤為突出。主要表現在：(1)經濟方面，社會主義市場經濟體制初步建立，但是經濟結構性矛盾和粗放式增長依然存在，人均生產力水平無法與發達國家相比。(2)社會方面，雖然人民生活達到了基本小康，但是存在十分明顯的城鄉發展不平衡，區域發展不平衡和收入分配不平衡問題，改變城鄉和區域社會發展差距任務十分艱巨。(3)環境發展方面，北方部分省份經濟發展過程中環境犧牲過大，帶來較為嚴重的空氣污染問題，東部省份各種高投入、低產出的產業模式導致大量的水環境污染。

如何實現區域經濟協調發展是世界各國均十分重視的課題，關于這方面的研究開始于上個世紀80年代，例如：Baumol(1986)提出最小命題論[1]，認為發展中國家經濟要想發展，必須首先沖破低水平均衡狀態，讓一部分區域先獲得發展；Harald(2002)提出了馬爾薩斯經濟發展理論[2]，將數學模型融入到發展中國家的資本收入評價中，該理論認為發展中國家會在低水平收入中反復輪回，才能慢慢達到平衡。

關于中國區域經濟的協調發展研究,目前研究成果較多，例如范敬雅等[3]利用EM算法改進高斯混合模型，對中國31個省份的GDP進行了分類擇優，驗證了該模型在特定情況下的可靠性；其他研究學者例如李澤宇、樊星和倪鵬飛等[4-7]從地理學角度、經濟學角度和傳統聚類分析角度對我國的GDP發展情況、物流產業發展情況和城市競爭力情況等進行了研究和實踐，均取得了較好的效果。本文依據改進的DEA聚類分析方法，對中國各地區的經濟發展狀況進行了分析和研究，提出了針對性評價建議。

1 基于改進聚類分析法

聚類算法是一種可以用于尋找數據之間內在聯系的計算方法，同時該方法也被稱為無監督學習法，在計算過程中聚類分析可以分成若干類別，主要為Q型聚類和R型聚類。考慮到中國區域地方經濟的相似性與經濟結構體系的復雜性和系統性，本文的研究采用聚類分析中的系統聚類法。系統聚類法主要采用如下步驟進行,如圖1所示。

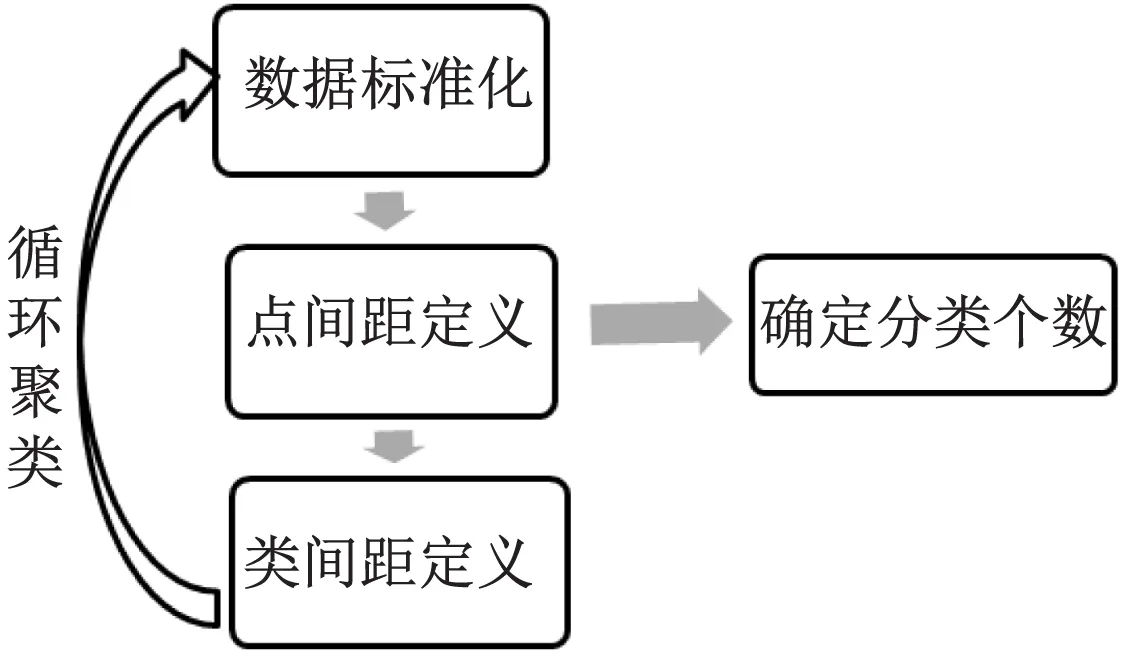
圖1 系統聚類法工作步驟

一般數據樣品中，假定該樣品具有m個特性指標，那么將該樣品作為一個矩陣來進行觀測。數據標準化過程中，n個樣品，每個樣品具有m個特性指標，因為無法進行直接分類處理，需進行標準化轉換,如式(1)。

(1)

經過數據變換后可以消除樣品內部的不同指標單位的差異，對于每個樣品的特征值，其平均值為0，標準差是1。

點間距指的是兩個樣品之間的絕對值距離，假定樣品A和樣品B的特征值分別為一個n維向量空間，對于A和B的距離進行定義，如式(2)。

(2)

類間距的計算過程與點間距類似，不再贅述。

本研究的聚類過程采用中間距離法，基于SAS軟件進行相關數據的融合分類，進行聚類分析時所采用的算法,如圖2所示。

圖2 聚類分析時采用的算法

2 區域協調發展評價指標建設

2.1 評價指標建設

依據經濟協調發展過程中的內涵問題，本文將經濟、社會、資源以及可持續發展能力作為協調發展的首要位置，尤其是城鄉區域發展協調性問題，并將其納入經濟協調性整體發展體系中。最后，提出了基于4個1級指標和15個2級指標的評價體系，如表1所示。

表1 區域經濟協調發展評價指標分類

2.2 數據處理

利用聚類分析中的AHP分析法(層次分析法)，該方法首先由美國運籌學家所提出來的一種多層次權重因子決策方法[8-9]，后來逐步被應用到經濟學分析中。基于層次分析的經濟協調發展評價步驟如下。

(1) 階梯層次結構建立。從一級指標開始，對每一級指標的下級分層情況進行分解至最后一層可以量化的指標，根據目標層級進行矩陣式排列，標明相近層級直接的邏輯關系，從而形成一個清晰的層次結構圖。

(2) 判斷矩陣建立。采用專家打分或者決策者回答，將目標層對于下一層級的影響程度進行量化打分，并賦予重要程度為1—9層級的標準值。

(3) 求解判斷矩陣。利用積分法進行求解判斷矩陣的向量和特征根，并將判斷矩陣進行歸一化處理。

(4) 各指標層的權重求解。根據判斷矩陣所求解出來的成果，對每一層次元素的重要性全脂進行一致性檢驗并求出量化標準值。

(5) 協調度計算。將五個一級指標的協調度以協調度系數進行表征，式如式(3)。

(3)

式中，C代表經濟協調度系數；A代表一級指標的權重量化標準值；N代表調節系數。本文中N取值為4，只有當A1—A5協同發展時C才能夠取得最大值，某一個指標偏低均會影響協調度系數C的大小。本文所劃定的經濟發展協調度等級，如表2所示。

表2 經濟協調性分級標準劃分

3 基于聚類分析法的成果分析

通過查閱中國2018年的各省級機構經濟發展基本狀況，采用本文第2節所擬定的4個一級指標，15個二級指標均衡發展評價指標體系，利用AHP法獲取不同省市的經濟發展協調度,如圖3所示。

圖3 全國經濟發展協調度指標(按%換算)

然后利用聚類分析法對其發展狀況進行評估,如表3所示。

表3 全國各省級城市經濟協調性聚類分析表

其中，由于香港、澳門和臺灣的經濟發展模式與政策導向與內陸省份差別較大，資料不容易收集，本文并未將其納入評價范圍。

從表3可以看出，經濟協調發展能力最為突出的是深圳、上海，其次為北京和廣州，同時還可以發現處于經濟發展失調類別的省份大多為西北部地區(約占47.2%)，處于失調和協調臨界范圍內的省份多為中東部省份，目前來看僅有15%左右的省份經濟發展處于協調狀態。說明我國目前在經濟發展協調性上依然處于低位，尤其是西部地區依然有很大改善空間。

為驗證該模型計算結果的準確性，本文對比2017年中國省市經濟發展的綜合得分情況以及基于PSO聚類分析方法的分析成果[4]，可以看出本文的研究成果與2017年中國經濟發展均衡性成果基本一致，說明本文的研究模型基本合理，如表4所示。

4 總結

我國目前存在的經濟發展不協調問題極大阻礙了我國社會主義現代化進程，如何對經濟發展過程中的平衡性進行合理評價是十分重要的課題。基于這一問題，本文提出基于AHP層次分析結合聚類分析的方法，對我國各省市五個方面的經濟均衡性發展指標進行了綜合評價并量化分析，得出如下結論。

表4 2017年中國區域經濟聚類分析發展水平

(1) 將聚類分析方法和AHP層次分析法結合為中國地區經濟協調發展的評價提供了一種更為精確和合理的評價方法，相比較傳統方法具有明顯優勢。

(2) 從分析結構來看，中國目前區域經濟協調性依然不容樂觀，大型直轄市經濟發展協調性良好，基本能夠實現社會、經濟、文化和生態等同步發展；中東部雖然處于協調和失調的臨界位置，但是具有非常好的經濟良性發展勢頭；西北部地區產業結構單一，經濟發展協調性差，統籌協調發展任務緊迫。

(3) 本文的研究基于歷史數據的反演，考慮的指標因此具有一定局限性，基本能夠合理評價中國區域經濟協調性中的狀態，希望今后的研究應從模型降維和算法智能化方向進一步深入。