基于多屬性的電力通信網節點重要度評價

彭舜杰， 張志海

(廣西電網公司 電力調度控制中心， 廣西 南寧 530023)

0 引言

在智能電網中，電力通信網承載著控制電網運行的狀態數據、調度數據和監控數據。電力通信網和電網緊密耦合，電力通信網的規模逐漸增大，節點眾多，拓撲復雜。為了保證電力系統的穩定運行，需要識別出電力通信網的重要節點。這些少量而重要的節點受到攻擊后，可能會對整個電網的結構和功能造成毀滅性的打擊。因此，電力通信網絡中節點的重要性評估一直是電力通信運維的重要工作之一[1]，也受到研究者的廣泛關注[2]。

電力通信網絡可以抽象為一種復雜網絡，利用復雜網絡的研究理論和算法分析電力通信網的節點重要性是一種切實可行的方式。文獻[3]分別從度中心性、中介中心性和結構中心性這三個角度分析網絡中節點的重要度。文獻[4]研究了網絡節點的局部關鍵性指標，考慮了相鄰節點及次相鄰節點的拓撲結構對網絡中節點重要性排序的影響。

以上文獻中僅考慮單一的指標，并對網絡中的節點重要性進行排序。然而分析節點重要性應綜合考慮多個指標對節點重要性的影響，從而降低節點重要度計算的片面性。文獻[2]通過綜合衡量節點傳輸能力和承載的業務重要度，并將其與網絡拓撲指標加權得到節點重要度。文獻[5]針對無向加權網絡提出了加權改進節點收縮法的節點重要性排序算法，使用熵權法為網絡邊賦權值，計算得到網絡的凝聚度值，將其作為原始網絡節點重要性度量。文獻[6]分析了度中心性、介數中心性、接近中心性、結構洞四個評價指標，利用基于層次分析法的TOPSIS算法對復雜網絡中的節點重要性進行了排序。但是引入層次分析法來確定節點重要性指標的權重，具有較強的主觀性。文獻[7]選取度中心性、介數中心性、緊密度、結構洞、K-核五個屬性指標，利用基于熵權法的TOPSIS算法來對節點重要性進行排序。雖然熵權法可以客觀地確定各個指標的權重，但是其只考慮單個指標之間的離散性，未考慮各個指標之間的相關性，最終會出現指標權重和節點重要性排序不符合實際情況的問題。

本文提出了一種基于多屬性決策的電力通信網節點重要性評價算法，該算法在確定指標的權重時，使用最大離差來計算指標的對比強度，并使用Kendall相關系數來評價指標之間的相關性。由于同時考慮了指標的對比度和相關性，使得指標權重更加客觀。接著將多個指標進行融合，通過計算各個方案與理想方案之間的逼近程度得出節點重要性的評價結果。仿真分析表明，本文所提方法能夠有效評價電力通信網絡節點的重要性。

1 節點重要度指標

電力通信網中的通信設備可以看作網絡節點，通信設備間的物理鏈路作為邊，把電力通信網絡抽象為一個無向網絡圖。圖中的每個節點具有局部和全局屬性，其中局部屬性僅表示一個節點在其相鄰的小區域網絡內的重要度，但是計算時間復雜度低；而全局屬性表示一個節點在整個網絡內的重要度，具有準確率高但計算復雜度高的特點。僅使用單一指標不能綜合地評價節點的重要性，因此本文分別選取局部、全局重要度和PageRank值作為節點重要性評價指標。在本文中約定：電力通信網絡的拓撲圖記為G(V,E)，其中V={v1,v2,…,vn}是節點集合，E={e1,e2,…,em}是邊的結合，n為節點數，m為邊數。

1.1 局部重要度

節點的局部重要度指的是節點在其局部區域的重要度，選取度中心性作為節點局部重要度。度中心性(Degree Centrality，DC)表示節點i相關的邊數與節點i可能存在的最大邊數的比值，如式(1)。

(1)

式中，di為節點i的度，即網絡中與該節點相連的邊數；N為網絡節點總數；N-1為任意節點可能存在的最大度。度中心性描述了一個節點與網絡中其它節點的直接連接的程度，其值越大，節點越重要。

1.2 全局重要度

全局重要度指標主要考慮網絡全局信息。介數中心性(Betweenness Centrality，BC)是通過假設信息僅沿著最短路徑來傳播，節點i的介數中心性,如式(2)。

(2)

式中，njk為連接節點j和k的最短路徑；njk(i)為節點j和k間最短路徑中包含節點i的路徑數目。介數中心性反應的是一個節點連接其他兩個節點的中介能力，其值越大，說明經過該節點的最短路徑數量越多，其在網絡中必具有重要的地位。用介數中心性代表節點的全局重要度。

1.3 PageRank值

PageRank算法認為某節點的重要性依賴于和它相鄰節點的重要性。如果一個節點和其他很多節點連接，那么該節點有較高的重要性。初始狀態，給每個節點設定相同的PageRank值。然后開始迭代，每一輪迭代把每個節點的PageRank值平均分配到它所指向的所有節點。每個節點的新PageRank值為其所獲得的所有PageRank值之和。經過若干輪迭代后，各節點的PageRank值會進入一個穩定的狀態。PageRank值越大的節點，表明越重要。第t次迭代時節點i的PageRank值,如式(3)。

(3)

式中，inputi為節點i的入度；|j|output為節點j出度；ε為阻尼系數，用于消除自環導致的影響，通常取ε=0.85。

2 基于多屬性的節點重要性綜合評價方法

評價節點重要性如果采用單一指標，會導致評價結果過于片面。對于電力通信網中的通信設備,其承載業務具有多樣性，評價重要性時需要綜合多方面因素。本節提出了一種基于多屬性決策的復雜網絡節點重要度的綜合排序方法，克服了單一指標的片面性。本算法在確定指標的權重時，不僅考慮了指標的對比強度，同時考慮了評價指標之間的相關性，計算得到的權重更加貼近實際。通過計算各個方案與理想方案之間的貼近度,得出節點重要性的排序結果。

2.1 指標規范化

設某待評價電力通信網共有N個節點，每個節點包含M個重要度指標，第i個節點的第j個指標值記為aij，分別計算各節點對應的多個指標值，得到節點指標矩陣,如式(4)。

A=(aij)N×M

(4)

由于選取的評價指標類型各不相同，可分為效益型指標和成本型指標，對不同類型的指標按照式(5)標準化處理，得到標準化指標矩陣H,如式(5)。

(5)

2.2 指標權重計算

本文算法從指標之間的對比度和相關性綜合決定指標權重。

指標之間的對比度用最大離差ζm表示,如式(6)。

(6)

式中，ζm的范圍為[0,1]，該值越大，說明在對應指標的區分度越大。

指標之間的相關性通過Kendall系數計算。第m個指標與其他指標的Kendall系數ηm,如式(7)。

(7)

式中，ηmt表示指標m與指標t之間的Kendall系數,如式(8)。

(8)

式中，D=2N/(N-1)；Nc和Nd分別為指標m與指標t組成的兩個N維列向量中變量排序值相等的變量對數目和不相等的變量對數目；s和k分別為矩陣H中指標m與指標t中相同元素分別組成的集合的個數；ui和vi分別為指標m與指標t中相同元素分別組成的集合中每個集合的元素個數。

若一個指標的對比強度越高，說明該指標分辨出各節點重要性的能力越強，權重應越大；若一個指標與其他指標之間的相關性越大，說明指標間的相似程度越高，應降低關聯性高的指標權重。依此得到指標m的客觀權重向量ωm的表達式,如式(9)。

(9)

2.3 節點重要度計算

將標準化矩陣H與權重向量ω相乘得到加權矩陣R,如式(10)。

R=(rij)N×M=(hij×ωj)N×M

(10)

確定正理想方案R+和負理想方案R-,如式(11)。

(11)

(12)

節點i的重要度就是其與正理想方案的貼近度Zi,如式(13)。

(13)

Zi值越高的節點，其重要程度越高。

3 仿真分析

為了驗證本文所提算法方法的有效性，以某省電力通信骨干網為例進行分析，如圖1所示。

圖1 某省電力通信網絡抽象拓撲圖

圖中隱去了節點實際位置，以序號代替。該網絡規模較小，各節點位置信息清晰，易于對各節點指標進行分析。其中2號節點為省級調度中心，1號節點為地區調度中心，14號節點為220 kV變電站，其余節點均為500 kV變電站。

本文采用文獻[8]中的算法NIAC作為對比算法。為了進一步驗證本文方法的有效性，使用網絡效率(Network Efficiency，NE)量化移除節點對網絡中物理拓撲的影響，進而分析網絡的魯棒性變化情況，其計算公式,如式(14)。

(14)

式中，N為網絡G的節點個數；V為網絡G的節點集合；dij為節點i與節點j的距離。

首先移除網絡中重要度排序靠前的節點，并計算網絡的拓撲結構的破壞程度的高低來評價節點重要度排序結果的有效性。根據本文和NIAC算法分別得到該電力通信網絡中的節點重要性排序，如表1所示。

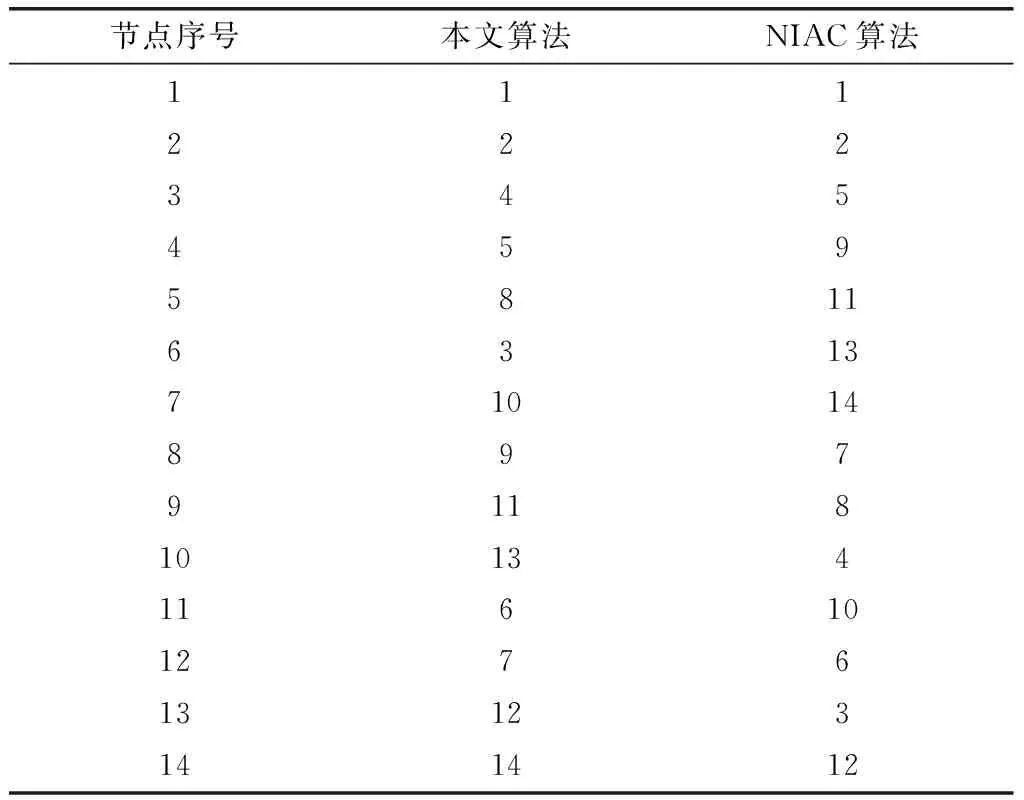
表1 節點重要性排序結果

按照節點重要性排序結果從大到小刪除該電力通信網絡中前30%的節點，得到網絡拓撲子圖，如圖2、圖3所示。

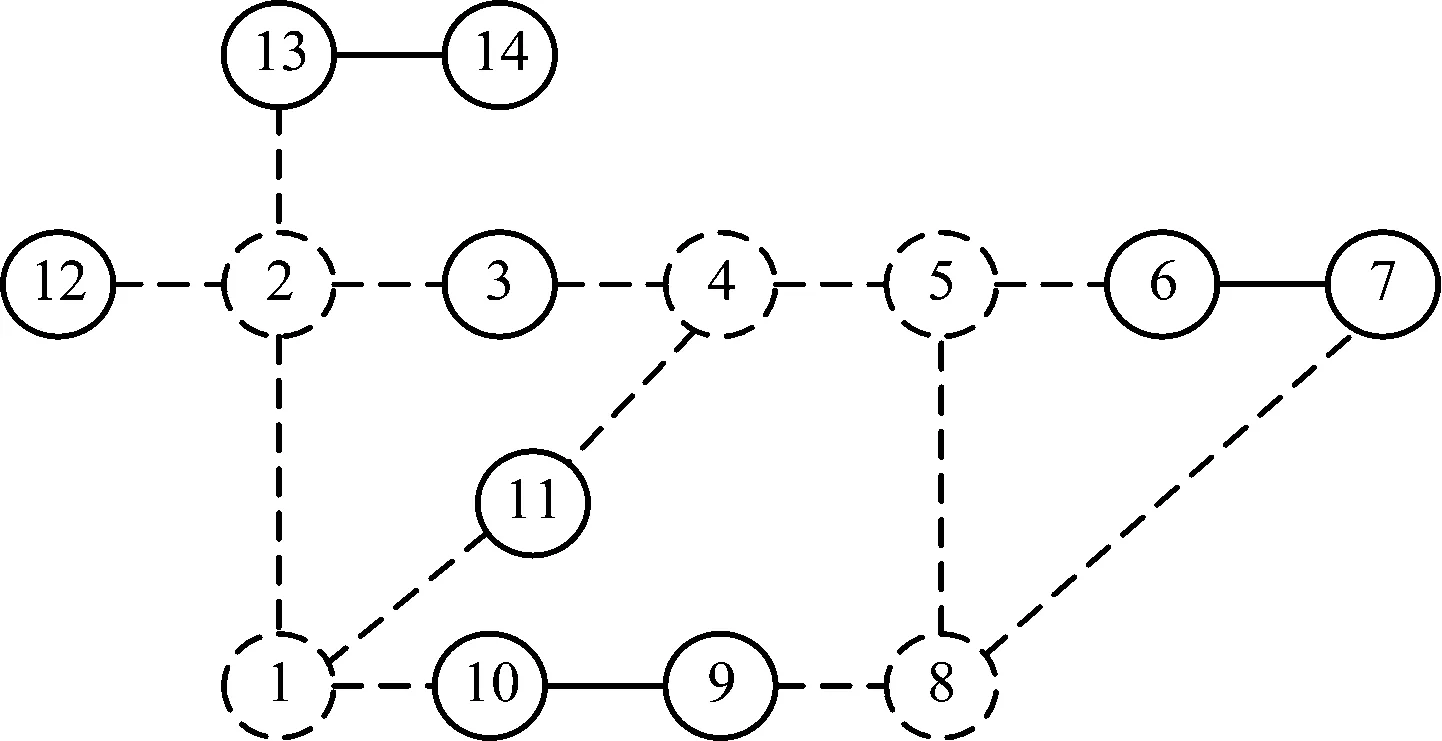
圖2 本文算法刪除前30%節點后的拓撲圖

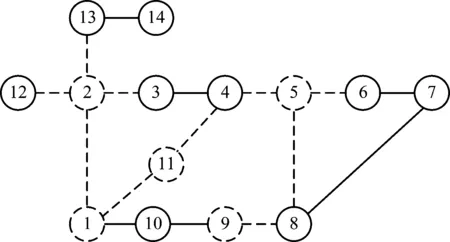
圖3 NIAC算法刪除前30%節點后的拓撲圖

通過刪除節點后的網絡拓撲子圖，可以看到本文使原網絡分解3個孤立點和3個孤立團體，網絡遭受到較嚴重的破壞；而對比算法最終得到2個孤立節點和3個團體，最大連通子圖數較大，網絡遭受的破壞程度較輕。

移除節點后網絡的效率變化情況，如圖4所示。

從圖4可以看出，由于本文算法采用多個指標對節點重要進行評價，網絡效率按照本文算法移除節點下降速度比NIAC算法較快，本文算法移除節點對網絡物理拓撲影響明顯優于NIAC算法。

4 總結

在分析電力通信網網絡中節點重要度時，使用單一重要度指標具有一定的片面性，因此需要綜合考慮多個指標來對節點進行評價。本文提出了一種基于多屬性決策的電力通信網節點重要度的辨識方法，綜合考慮節點度中心性、介數中心性、PageRank三個指標進行融合，通過計算各個方案與理想方案之間的逼近程度得出節點重要性的排序結果。本文算法在確定指標權重時考慮了各指標的對比性和相關性，使得得到的權重更加貼近實際。根據所得結果與相關文獻結果進行仿真分析，結果表明本文方法更加準確，能更好地識別電力通信中的重要節點。

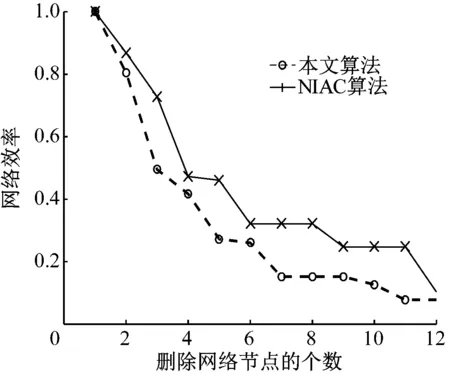
圖4 刪除節點后NE值比較