基于等價地貌參數的地貌單位線在羊昌河流域的構建與應用

張程玥 朱少成

摘 要：基于霍頓-斯特拉勒河流分級法建立的傳統地貌單位線（GIUH）廣泛應用于缺資料山區的匯流計算中，然而該法確定的地貌參數隨選取面積閾值的改變并不唯一，進而使得生成的GIUH出現較大隨意性。本文采取獨立于面積閾值的等價地貌參數確定方法，使用90M分辨率DEM數據提取羊昌河黃貓村控制站以上流域，建立地貌單位線匯流模型，并結合新安江模型的產流、分水源計算方法，在1985到2012年間選取8場實測洪水過程進行模擬與實測值進行比較。結果表明，基于等價地貌參數的地貌瞬時單位線在次洪的峰洪峰及峰現時間的模擬均取得了較好的模擬結果，可推廣至無資料山區應用。

關鍵詞：等價地貌參數;GIUH;產匯流分析;羊昌河流域

1 緒論

流域水文響應和流域地貌特征緊密相關，在流域匯流過程中，需要區別對待大小河流不同的匯流特性，而通過寬度函數[1，2]描述地貌擴散作用或通過霍頓-斯特拉勒河流分級法所確定的地貌單位線能結合數字高程模型（DEM），相對于基于某場洪水而確定的單位線具有明確的物理依據，且對水文資料的依賴也較小。盡管基于霍頓-斯特拉勒河流分級法的地貌單位線因為計算較簡單，在水文地貌學及山區缺少資料地區的匯流計算中應用廣泛，然而在實際應用的過程中，該分級法對低級河流的數目十分敏感，導致定量引入的地貌因子極易改變。例如由Ocallaghan和Mark提出的目前廣泛應用的河網提取方法[3，4]，其中引入了集水面積閾值的概念。天然河網中的每一個水道都有自己的匯水范圍，對同一個流域，選取不同的集水面積閾值將得到不同的河網，進而對流域寬度函數分布及河流分級均造成較大影響，使得計算出的地貌單位線結果具有較大的差異[5]

本文利用獨立于面積閾值的等價地貌參數確定方法[6]，通過建立河源數、總河長與集水面積閾值的函數關系，提取RBe、RLe、RAe、Le四個參數，排除了在利用DEM提取流域水系時確定集水面積閾值的主觀性，并選取羊昌河黃貓村控制站以上流域提取地貌單位線，結合新安江模型的產流、分水源計算方法，模擬1985—2012年間的8場洪水過程，并與不同面積閾值下得到的洪水過程進行對比。計算分析表明，基于等價地貌參數的地貌單位線在羊昌河流域的匯流中取得了良好的模擬效果，可推廣至無資料山區進行應用。

2 基于等價地貌參數的單位線原理

2.1 集水面積閾值的確定對GIUH影響

由霍頓-斯特拉勒河流分級法確定地貌單位線計算公式，GIUH的確定僅與RB、RL、RA、LΩ四個源于地貌的參數[7]及匯流速度v有關，而四個地貌參數受提取河網時面積閾值影響較大。

合理的面積閾值范圍下提取的河網能與地形圖上的“藍線”河網相吻合，而“藍線”與實際河網相比幾乎永遠是不完整的。然而，人為方法增加河道后，斯特拉勒分級法不可避免地使得最高級河流的河長短于實際長度[6];而依據實驗中出現的增加集水面積閾值河網密度變化趨緩的現象確定坡地網鏈全部消失的閾值點作為集水面積閾值也具受到一定的人為主觀判斷影響，所以集水面積閾值的確定既復雜又無精確的方法。

以羊昌河黃貓村水文站以上流域為例，分別取不同集水面積閾值，經河網分級后由得到的地貌參數值表1可知，當面積閾值由2km2增加至7.2 km2時，河網數由4減少到3。由于低級河流數量減少明顯，但對應的控制面積增加較高級河流快，因此RB、RA分別出現增大、減小的趨勢，給單位線的計算結果帶來很大的不確定性。

2.2 等價參數確定的地貌單位線

針對這一問題，Moussa提出了等價地貌參數替代原有的地貌因子[6]，公式如下：RBe、RLe、RAe、Le分別為等價的分叉率、河長率、面積率、最高級河流長度：

將上一步得到的三個參數值代入，此時確定的a、k值是唯一的，進而求出唯一GIUH。

3 研究區概況及應用實例

3.1 研究區概況

羊昌河流域位于云貴高原苗嶺山脈北坡，發源于安順市西秀區頭鋪，至平壩縣焦家橋附近入紅楓湖，為烏江水系貓跳河的一級支流[9]。研究利用2000年普查得到的土地利用矢量數據，對羊昌河流域土地利用進行統計，流域土地利用主要以山區耕地為主，所占面積為365.02km2，約占整個流域面積的48%;其次林地面積最大，為250.72km2;研究選擇黃貓村水文站點以上集水流域作為研究區域，利用分辨率90m的DEM獲取流域地形圖，面積為719.45km2。黃貓村水文站位于東經106°26′，北緯26°23′，為羊昌河控制站。水系由面積閾值取5.4km2時產生的河網進行柵格化得到，此時的水系與地形圖上“藍線”較為吻合。

3.2 等價地貌單位線提取

3.2.1 等價地貌參數

為了確定式（6）（7）中的三個參數，首先利用ArcGis導入羊昌河黃貓村站以上DEM數據，集水面積閾值取2～72km2間多個值，分別提取對應河網得到河源數n及總河長T。不斷增加面積閾值發現S取到130.5km2時，流域只剩一條河流，此時對應的河長即為m1=44.08km。其次以面積閾值為自變量，分別點繪河源數n及總河長T，擬合得到參數λ、α、b分別為0.412、0.9809、0.3976，符合一般河流取值范圍;最后將以上三個參數直接代入公式（6）（7）得到唯一的a=3.242177、k=32.86805。

3.2.2 流速v的確定

地貌單位線假設水流點相關而非獨立，即認為水流是線性的。流域面積越小，匯流的非線性作用越大，則越需要考慮到流域地貌特征以及凈雨強度對流速的影響，考慮到羊昌河流域面積超過300km2不屬于小流域，忽略凈雨強度，只考慮地貌特征對流速的影響。

選取1982年R.L.Bras建立的基于運動波理論的經驗流速公式[10]。糙率取0.055，坡降取1.2%，計算得流速v為269m/s。

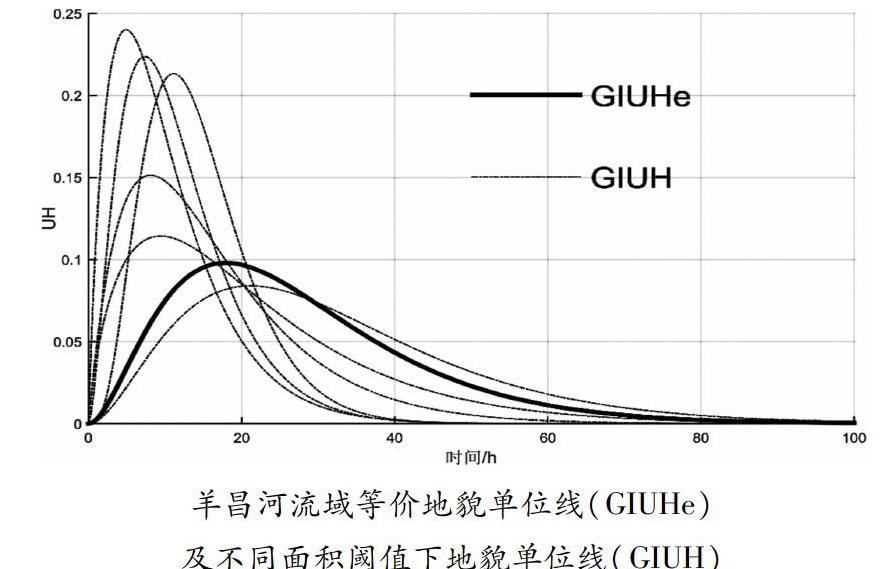
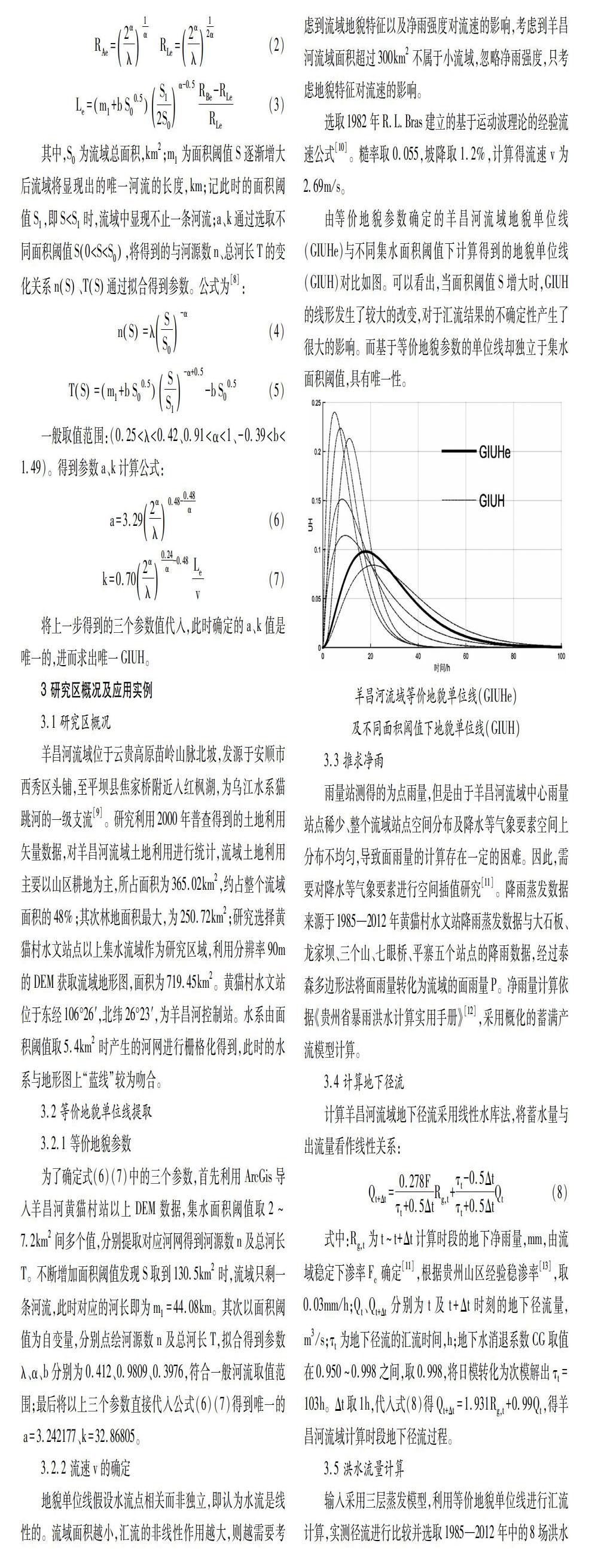
由等價地貌參數確定的羊昌河流域地貌單位線（GIUHe）與不同集水面積閾值下計算得到的地貌單位線（GIUH）對比如圖。可以看出，當面積閾值S增大時，GIUH的線形發生了較大的改變，對于匯流結果的不確定性產生了很大的影響。而基于等價地貌參數的單位線卻獨立于集水面積閾值，具有唯一性。

3.3 推求凈雨

雨量站測得的為點雨量，但是由于羊昌河流域中心雨量站點稀少、整個流域站點空間分布及降水等氣象要素空間上分布不均勻，導致面雨量的計算存在一定的困難。因此，需要對降水等氣象要素進行空間插值研究[11]。降雨蒸發數據來源于1985—2012年黃貓村水文站降雨蒸發數據與大石板、龍家壩、三個山、七眼橋、平寨五個站點的降雨數據，經過泰森多邊形法將面雨量轉化為流域的面雨量P。凈雨量計算依據《貴州省暴雨洪水計算實用手冊》[12]，采用概化的蓄滿產流模型計算。

3.4 計算地下徑流

計算羊昌河流域地下徑流采用線性水庫法，將蓄水量與出流量看作線性關系：

3.5 洪水流量計算

輸入采用三層蒸發模型，利用等價地貌單位線進行匯流計算，實測徑流進行比較并選取1985—2012年中的8場洪水資料進行檢驗;同樣輸入情況下，分別利用面積閾值2km2、54km2、7.2km2生成的地貌單位線進行匯流計算與實測洪水進行比較，結果如表2、表3所示：

由表2、3可知，無論是洪峰還是峰現時間，基于等價地貌參數的地貌單位線所得的結果都更接近實測值，且易觀察到集水面積閾值取值對洪水預報的影響很大。

4 結論

本文采用等價地貌參數，以羊昌河流域為研究對象構建了以地貌單位線為基礎的流域匯流模型，并采用該模型對1985—2012年間8場次洪過程進行流域匯流演算對比分析。計算的分析結果表明，基于等價地貌參數的地貌單位線在羊昌河流域的匯流應用取得了良好的效果。

通過對等價地貌單位線在羊昌河流域的模擬結果分析，存在以下問題：盡管數值上更接近實測值，基于等價參數地貌單位線模擬洪峰整體偏小，考慮到可能的原因有a.等價地貌參數的計算過程中雖然避免了面積閾值S的選取對結果的影響，但是以等價公式確定的α、k值計算的GIUHe線型較坦化，某些次洪過程出現洪峰偏小的情況。b.羊昌河流域所屬地區喀斯特地貌發育，地下常年存在巖溶裂隙水，按一般線性水庫法算出的地下徑流量偏小。c.不同降雨雨型對峰量影響較大，羊昌河流域降雨雨峰多集中在前中時段，帶來的洪峰量更大。

參考文獻：

[1]A.J.Surkan.Synthetic Hydrographs：Effects of Network Geometry[J].Water Resources Research，1969，5（1）：112-128.

[2]I.Rodríguez-Iturbe，M.González-Sanabria，R.L.Bras.A geomorphoclimatic theory of the instantaneous unit hydrograph[J].Water Resources Research，1982，18（4）：877-886.

[3]J.F.O′Callaghan，D.M.Mark.The extraction of drainage networks from digital elevation data[J].Computer Vision Graphics & Image Processing，1984，28（3）：323-344.

[4]孔凡哲，李莉莉.利用DEM提取河網時集水面積閾值的確定[J].水電能源科學，2005，23（4）：65-67.

[5]A.Tribe.Automated recognition of valley lines and drainage networks from grid digital elevation models：a review and a new method[J].Journal of Hydrology，1992，167（s1-4）：393-396.

[6]R.Moussa.Definition of new equivalent indices of Horton-Strahler ratios for the derivation of the Geomorphological Instantaneous Unit Hydrograph[J].Water Resources Research，2009，45（9）：63-69.

[7]芮孝芳.地貌瞬時單位線研究進展[J].水科學進展，1999，10：345-350.

[8]陳穎冰，石朋，胡健偉，等.基于等價地貌參數的地貌單位線確定方法[J].水電能源科學，2017，35（5）：18-20.

[9]梁瑞駒，潘永新.推求無資料地區設計洪水的一種方法[J].水科學進展，1997，8：65-72.

[10]徐韜，高益輝，俞祎波，等.缺資料山丘區的洪水模擬與情景分析[J].中國農村水利水電，2015，2015（11）：173-177.

[11]鄭鑫，楊濤，師鵬飛，等.缺資料地區日降雨空間插值方法研究[J].中國農村水利水電，2017，13-16.

[12]貴州省水利電力廳.貴州省暴雨洪水計算實用手冊[M].貴陽：貴州省水利電力廳，1983.

[13]成小松，劉宗義.淺析貴州省地下水資源評價中的基流分割[J].貴州水力發電，2006，20：11-14.