壓電宏纖維驅動的仿生尾鰭微推進力測量系統?

孟浩鋒，楊依領，2， 婁軍強，2， 馬劍強， 崔玉國，陳特歡，2

（1.寧波大學機械工程與力學學院 寧波，315211）（2.浙江大學浙江省先進制造技術重點實驗室 杭州，310027）

引言

魚類在長期的自然選擇中形成了獨特的外形和出色的游動能力。根據魚類的身體形狀和游動模式可將其推進方式簡單地分為身體/尾鰭（body or caudal fin，簡稱BCF）和中鰭/對鰭（media or paired fin，簡稱MPF）兩種。鲹科魚類的BCF推進模式更是公認的效率較高、游速較快的游動模式［1］。與傳統螺旋槳推動的水下航行裝置相比，模仿鲹科魚類BCF推進模式的水下仿生推進器具有較好的水下運動能力，在海洋資源勘探、軍事監視、生物觀察及水下工程等領域展現出了廣闊的應用前景和巨大的潛在價值［2］。

智能材料與結構的發展為水下仿生推進器提供了新的驅動方式，有助于實現推進器系統的小型化、集成化和智能化［3］。Nguyen等［4］利用4組壓電陶瓷片驅動4桿機構模擬魚尾往復擺動，設計了壓電陶瓷驅動的水下機器魚。Coral等［5］采用多條形狀記憶合金絲驅動柔性仿魚脊柱結構彎曲變形，提出一種仿鱸魚水下推進器。Cheng［6］設計了一種離子基聚合物驅動的仿生尾鰭，并用于水下機器魚的推進。近年來，美國Smart Material公司商業化了美國NASA研發的新型纖維基壓電復合材料（MFC）。基于環氧樹脂復合和指叉電極技術的MFC具有柔性好、驅動力大、動態響應好、變形能力強且防水性好的優點［7］。Shahab等［8］研究了MFC驅動的柔性懸臂梁結構的水下動態響應，并建立了結構-電-流體 耦 合動力 學 模 型。Lou等［9］提出 的MFC驅動的仿魚形水下推進器的游動速度可達174 mm/s（0.58身長比/s），證實了MFC驅動器在柔性結構變形控制及水下仿生驅動領域的巨大優勢和有益效果。

推進力的變化情況是反映推進器推進性能的重要 指標。Nguyen等［10］采用ATI的6軸力傳 感 器測量了壓電陶瓷驅動的水下仿生機器魚在不同驅動頻率下產生的平均推進力變化結果。Gao等［11］利用懸臂式微型力傳感器測量了形狀記憶合金絲驅動的仿生墨魚噴射式推進器在不同驅動電壓下的推進力變化情況。同樣采用ATI的六軸力傳感器，Hubbard等［12］測到離子基聚合物驅動的水下仿生尾鰭擺動過程產生的最大平均推進力為0.4 mN，但是所采用傳感器分辨率僅為0.149 mN。由于智能材料驅動的水下仿生推進器產生的推進力大多在毫牛級別，如何設計出測量精度較高、結構簡單可靠且安裝方便的水下微推進力測量系統，是研究水下仿生推進器動態推進特性的基礎，也是分析改善其推進性能的重要手段［13］。

筆者模仿錦鯉的尾部特征及BCF推進方式，設計了一種MFC驅動的柔性仿錦鯉尾鰭，并結合柔性尾鰭水下擺動過程的受力情況，推導計算了懸臂式微推進力測量機構的特性指標參數，設計出用于柔性仿生尾鰭推進力動態精密測量的懸臂式微推進力測量系統。文中搭建了柔性仿生尾鰭微推進力測控系統，并進行了參數標定擬合實驗，通過測試得到了MFC驅動的柔性仿生尾鰭的水下擺動特性。基于設計的推進力測量裝置，開展了MFC驅動的柔性仿生尾鰭在不同驅動條件下的微推進力動態測量實驗。

1 MFC驅動的柔性仿生尾鰭結構描述

MFC將矩形截面壓電宏纖維和環氧樹脂以特定的排列方式粘貼在一起，并采用特殊工藝將指叉電極蝕刻在包銅聚酰亞胺薄膜上。壓電纖維和環氧樹脂的排布方式提高了復合物的柔韌性，不容易出現脆性斷裂，顯著提高提高了MFC的使用壽命；指叉電極使得沿著纖維軸向方向的施加電場鋪滿整個壓電纖維層，能夠在d33工作模式下較傳統壓電陶瓷片產生更大的驅動力和輸出位移。因此，MFC驅動器具有質量輕、柔性好、驅動力大且防水性能好等優點，是水下柔性仿生結構較為理想的驅動元件。其基本結構及實物如圖1所示。

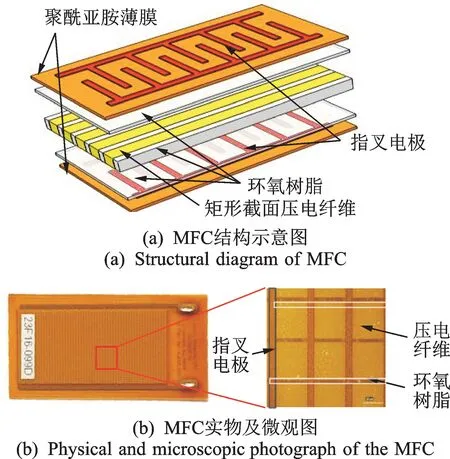
圖1 MFC結構示意圖及實物圖Fig.1 Structure diagram and photograph of the MFC actuator

錦鯉身體細長，呈紡錘形，具有優美的游動姿態，是一種遍布全世界的高檔觀賞魚類［14］，其實體見圖2（a）。從形態學和運動學特征上分析：錦鯉屬于典型的鲹科BCF模式，主要依靠身體兩側肌肉帶動尾鰭往復擺動實現推進。對錦鯉尾柄和尾鰭進行形態輪廓提取，設計出MFC驅動的柔性仿生尾鰭結構（見圖2（b）），其尾柄寬度bs、尾鰭展長le、尾鰭弦長lh分別為20，46.6，66 mm，其總體長度ls為89.6 mm，基體厚度為0.2 mm。以仿錦鯉尾鰭形狀的1100鋁合金柔性薄板為基體，并留出夾持域。采用美國Smart Material Corp.生產的d33模式的壓電宏纖維復合材料MFC 2814-P1（其尺寸為38 mm×20 mm×0.6 mm，其中有效尺寸為28 mm×14 mm×0.3 mm）為驅動器，兩片MFC驅動器通過環氧樹脂膠DP460對稱地粘貼在柔性基體的根部位置。當MFC受到正向電壓時，在d33模式的逆壓電效應下，MFC沿著基體纖維長度方向產生伸長形變，帶動柔性仿生尾鰭向上擺動；而當MFC受到負向電壓時，相應地產生收縮形變，進而帶動柔性尾鰭向下擺動。在交變電壓作用下，柔性基體在MFC致動下產生往復擺動，模仿錦鯉尾鰭BCF擺動推進模式如圖2（c）所示。

圖2 MFC驅動的柔性仿生尾鰭結構和工作模式圖Fig.2 Structure diagram and working mode of the flexible biomimetic fin driven by MFC actuators

2 懸臂式微推進力測量結構設計

2.1 水下仿生柔性尾鰭擺動過程受力分析

在柔性仿生尾鰭推進過程中，MFC驅動器在驅動電壓下主動變形帶動柔性尾鰭產生擺動動作，柔性尾鰭在擺動過程中將周圍水體排開，而周圍水體在擺動方向接觸面上對柔性仿生尾鰭產生壓力作用，整個尾鰭結構的受力情況如圖3所示。柔性仿生尾鰭從上極限位置擺動到中間位置過程中，驅動力矩MMFC、尾鰭擺速v以及周圍流體對擺動尾鰭作用壓力及合力F見圖3。考慮到柔性尾鰭的推進方式，將水壓力合力F分解為沿前進方向的推進力FT以及與推進力方向垂直的側向力FL。顯然仿生柔性尾鰭在FT作用下產生沿著x軸正方向的推進運動。

圖3 水下柔性仿生尾鰭受力示意圖Fig.3 Force diagram of the underwater flexible biometric fin

需要指出的是，受MFC驅動器本身的驅動能力及流體環境阻力的影響，柔性仿生尾鰭的水下擺動幅度較小，從而導致水壓力合力F分解產生的側向力FL遠大于推進力FT，因此在MFC驅動的柔性仿生尾鰭推進力測量過程中，必須采取一定措施減小側向力干擾的影響。

2.2 懸臂式微推進力測量裝置設計

推進力是研究柔性仿生尾鰭推進性能的一個重要指標。為了測量MFC驅動的柔性仿生尾鰭在擺動過程中產生的推進力大小，設計懸臂式微推進力測量裝置如圖4所示。

仿生柔性尾鰭在MFC驅動下的擺動過程中，柔性尾鰭在推進力FT作用下產生沿著x軸正方向的推進運動，測力構件產生相應的彈性變形。由于測力構件為典型的細長梁構件，在假設測力構件純彎曲變形的情況下，其撓曲線的近似微分方程為

其 中：EAl，I，L和b分別為測力構件的 彈性模量、截面慣性矩、長度和寬度；w（z）為構件上任意一點的變形撓度。

圖4 微推進力測量系統示意圖Fig.4 Diagram of the micro-thrust measurement system

由測力構件上端滿足固定邊界條件，可得在推進力FT作用下，測力構件末端的變形位移為

其中：Kw為測力梁構件在推進力FT作用下彎曲剛度，單位為mN/mm。

由于仿生柔性尾鰭在擺動過程中還受到側向力FL的作用，從而發生垂直于截面的自由扭轉變形。對于矩形截面的測力構件，根據經典彈性力學理論的變形協調方程［15］

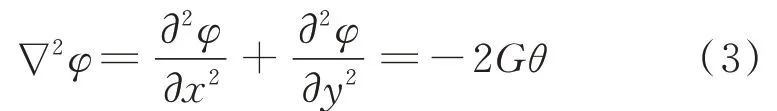
其中：φ為矩形截面的應力函數；G和θ分別為測力構件的剪切模量和單位長度的相對扭轉角。

由于應力函數φ在矩形截面邊界上的切應力分量為零，滿足如下邊界條件

測力構件矩形截面滿足單連通區域條件，式（3）常系數線性微分方程的解滿足Poisson方程特解加上對應的Laplace方程通解的形式。計算可得單位長度的相對扭轉角θ為

其中：α為取決于矩形截面長寬比的常量，當b＞10t時，α約為0.312；ML為測力構件受到的側向力扭矩。

結合式（5），可得測力梁構件在側向力FL作用下扭轉產生的變形位移為

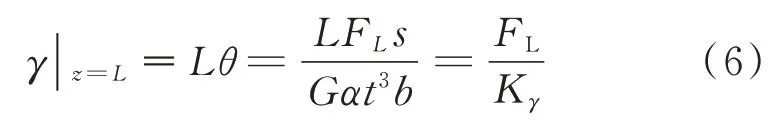
其中：s為側向力FL到測力構件扭轉中心的力臂；Kγ為測力梁構件在側向力FL作用下的扭轉剛度，單位為mN/mm。

由于測力構件為典型的細長梁構件，根據歐拉-伯努利梁理論，其固有頻率計算公式為

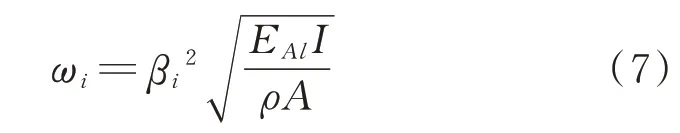
其中：β，ρ和A分別為測力梁構件的特征頻率、彈性模量和橫截面積。

選用輕質、彈性好的鋁合金1100作為測力構件材料。綜合考慮柔性仿生尾鰭推進力測量精度及測力構件變形位移檢測精度需求，并盡量減少柔性尾鰭擺動過程中側向力引起的測力構件扭轉變形對推進力作用下彎曲變形的干擾。考慮到MFC驅動的仿生尾鰭產生的周期力，必須避免推進力在測力構件上引起測量系統的共振，需盡量提高測力構件的固有頻率。提出測力梁構件尺寸參數的指標為

根據式（8）確定的設計指標，初步確定懸臂式測力梁構件的尺寸參數。基于測力梁構件的實測尺寸計算得到其彎曲剛度Kw和扭轉剛度Kγ分別為298.7和60.95 mN/mm，一階固有頻率ω為235.7 rad/s。測力構件的實測尺寸和特征參數計算結果見表1。

表1 測力梁構件參數表Tab.1 Parameters of the force measurement cantilever

3 MFC驅動的柔性仿生尾鰭微推進力測量

3.1 柔性仿生尾鰭微推進力測控系統搭建

搭建柔性仿生尾鰭微推進力測控系統如圖5所示。測試過程中，PC機發出的控制信號經嵌入在NI-cDAQ9178機箱上的D/A模塊NI-AO9263轉換為模擬電壓輸出，并通過功率放器Trek-ZD700A放大200倍后施加到MFC驅動器上，從而驅動柔性仿生尾鰭產生往復擺動。測力梁構件在柔性仿生尾鰭推進力作用下產生變形，利用安裝在梁構件末端的激光位移傳感器（Keyence，LK-G80，分辨率為0.15μm）檢測測力梁構件的變形位移，該信號經控制器調理后，通過嵌入在機箱上的A/D模塊NIAI9205轉換為數字信號傳輸到PC中。同時利用安裝在仿生柔性尾鰭端部的激光位移傳感器（Micro-Epsilon，ILD2200-10，分辨率為0.3μm）實時采集柔性尾鰭的擺動位移。整個測試系統控制平臺通過LabVIEW軟件程序完成。

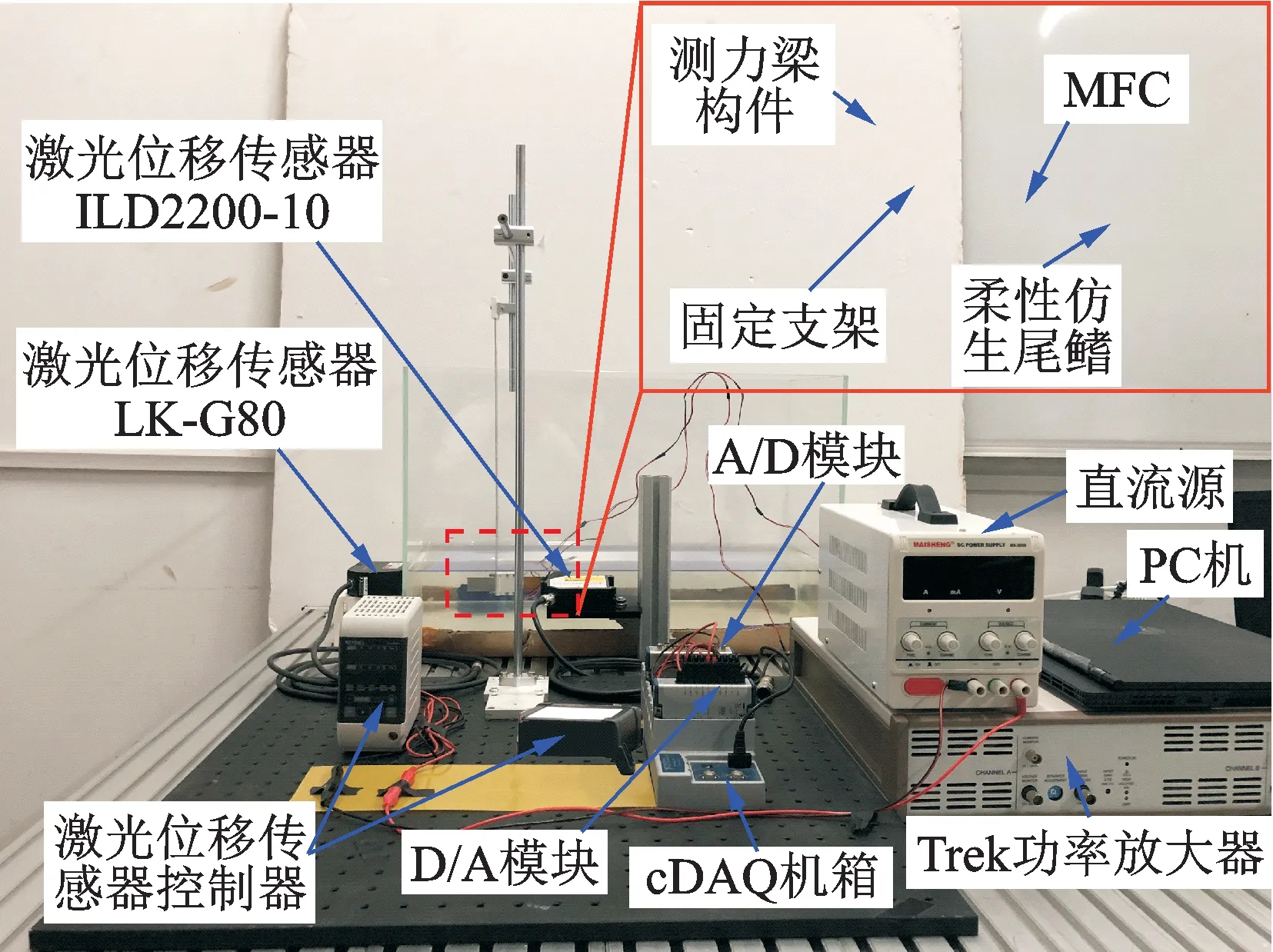
圖5 柔性仿生尾鰭微推進力測控系統實物裝置圖Fig.5 Experimental setup of the micro-force measurement system for the flexible biomimetic fin

3.2 測力梁構件彎曲剛度標定

對測力構件進行敲擊實驗，得到其功率譜密度函數曲線如圖6所示，其實測固有頻率為235.5 rad/s（37.5 Hz），與設計指標基本一致。由于水下仿生尾鰭的擺動頻率一般低于10 Hz，遠離測力梁構件的共振區，且測力梁構件在低頻段的響應輸出變化較為平緩，故可認為測力梁構件的動態特性滿足實驗要求。

圖6 測力梁構件功率譜密度函數曲線Fig.6 Power spectral density of the cantilever

為了標定測力梁構件的實際彎曲剛度，將測力梁構件水平放置，實驗測定空氣中的梁構件在標準砝碼重力作用下的末端變形位移。標定過程中，以梁構件在自身重力作用下的變形位置為初始位置，以100 mg的標準片狀砝碼增量，得到砝碼質量與測力梁構件變形位移之間關系如表2所示。

表2 砝碼與測力梁構件變形位移關系表Tab.2 Relationship between the weights and cantile?ver deflection

以砝碼重力xi為自變量，測力梁構件變形位移yi為因變量，采用最小二乘法對二者進行線性擬合，計算擬合直線斜率k和截距f為

其中：xˉ和yˉ為砝碼重力xi和梁構件變形yi的期望。

計算得到斜率k（即彎曲剛度Kw）和截距f分別為298.7 mN/mm和0.005 2 mN，相關標定實測數據和擬合直線如圖7所示。顯然，擬合直線斜率即為測力梁構件的彎曲剛度，其實際擬合值為298.7 mN/mm，略小于理論設計值310.2 mN/mm，這是由于梁構件的標稱結構參數與實際略有差異所致。而0.005 2 mN的零點漂移現象由擬合誤差及測力梁構件重力的影響產生。

4 柔性仿生尾鰭動態性能測試

4.1 柔性仿生尾鰭擺動性能測試

圖7 砝碼重力與梁構件變形擬合直線Fig.7 Fitting line between the weight gravity and cantilever deflection

將柔性仿生尾鰭固定在水箱中部位置，盡量避免箱體壁面效應對仿生尾鰭結構水下動態特性的影響。由于MFC驅動的柔性仿生尾鰭在諧振模式下可獲取較好的擺動性能，考慮到MFC驅動器的受控電壓范圍-500～1 500 V，故采用頻率范圍0.1～15 Hz、幅值為400 V的正弦掃頻激勵電壓信號施加到MFC上。得到MFC驅動的柔性仿生尾鰭末端的水下擺動位移頻率響應曲線如圖8所示，可以看出柔性仿生尾鰭的水下一階固有頻率在7 Hz附近。

圖8 柔性仿生尾鰭末端的水下擺動位移頻響曲線Fig.8 Underwater frequency response of the oscillation displacement of the fin

掃頻過程中激勵頻率連續變化，導致柔性仿生尾鰭擺動過程中引起的周圍流體運動處于不穩定狀態，因此掃頻測試只能粗略獲取柔性仿生尾鰭一階固有頻率范圍。為了獲取MFC驅動下柔性仿生尾鰭的水下動態特性，進行了仿生尾鰭在單一頻率正弦信號激勵下的穩定擺動測試。測試中選取頻率范圍3～9 Hz（頻率間隔0.1 Hz）、共60組正弦激勵電壓信號，激勵信號幅值為400 V，激勵時間為20 s。得到柔性仿生尾鰭末端的穩定擺動位移幅值（峰峰值）與擺速幅值隨著激勵信號頻率的變化曲線如圖9所示。測試結果表明：MFC驅動的柔性仿生尾鰭在7 Hz時取得最大擺幅峰峰值5.08 mm，由于柔性尾鰭的擺速與其擺幅及擺頻有關，故在略高于固有頻率的8 Hz處取得最大擺速83.12 mm/s。

圖9 柔性仿生尾鰭的水下擺幅與擺速曲線Fig.9 Oscillation displacement and velocity of the fin

4.2 柔性仿生尾鰭微推進力測量

基于Lighthill細長體理論，對于截面一致的細長結構，周圍流體以虛擬附加質量形式作用到往復擺動的結構上，進而產生推進效果。不考慮水流速度，細長體結構在一個擺動周期內產生的平均推進力［16］為其中：β為虛擬質量系數；ρw為流體密度；b為細長結構截面寬度；vavg為細長體結構末端平均擺速。

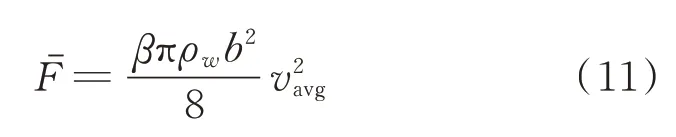
類比截面一致的細長體結構，柔性仿生尾鰭產生的推進力大小也與其末端擺速正相關，故選取柔性仿生尾鰭在獲取最大擺速104.3 mm/s時的激勵條件（激勵頻率為8 Hz，電壓幅值為400 V，激勵時間為20 s）進行了推進力測量實驗。從柔性仿生尾鰭產生的推進力變化過程（圖10）中可以看出：初始階段，周圍流體在柔性尾鰭的帶動下由靜止狀態逐漸流動起來，低速流體較大的黏滯力相應地導致柔性尾鰭產生較大的推進力；穩定階段，周圍流體在柔性尾鰭擺動過程中逐漸形成穩定的渦流狀態，使得柔性尾鰭產生的推進力也基本趨于穩定狀態；停止階段，MFC驅動信號停止后，柔性尾鰭的擺動行為在周圍流體阻力作用下迅速停止，相應產生的推進力也很快減小到零。

圖10 8 Hz下柔性仿生尾鰭擺動產生的推進力變化Fig.10 Variation of the thrust generated by the oscillation fin with the excitation frequency of 8 Hz

圖11 進一步給出了在柔性尾鰭穩定擺動階段，7 Hz頻率時MFC驅動電壓信號、尾鰭末端擺動位移以及產生推進力的對比變化情況。從圖中可以看出柔性尾鰭產生的推進力變化周期是其擺動周期的一半，這是由于仿生尾鰭在外擺和回擺過程中交替產生一對旋向相反的流體渦環結構所致［17］。在一個穩定的擺動周期內，尾鰭擺動產生的推進力在65.6%周期內取值均大于零（沿著x正方向），從而產生推進效果；而在34.4%周期內沿著x負方向，產生拖拽作用。尾鰭擺動產生的瞬時最大推進力和拖拽力分別為6.26和-2.5 mN。

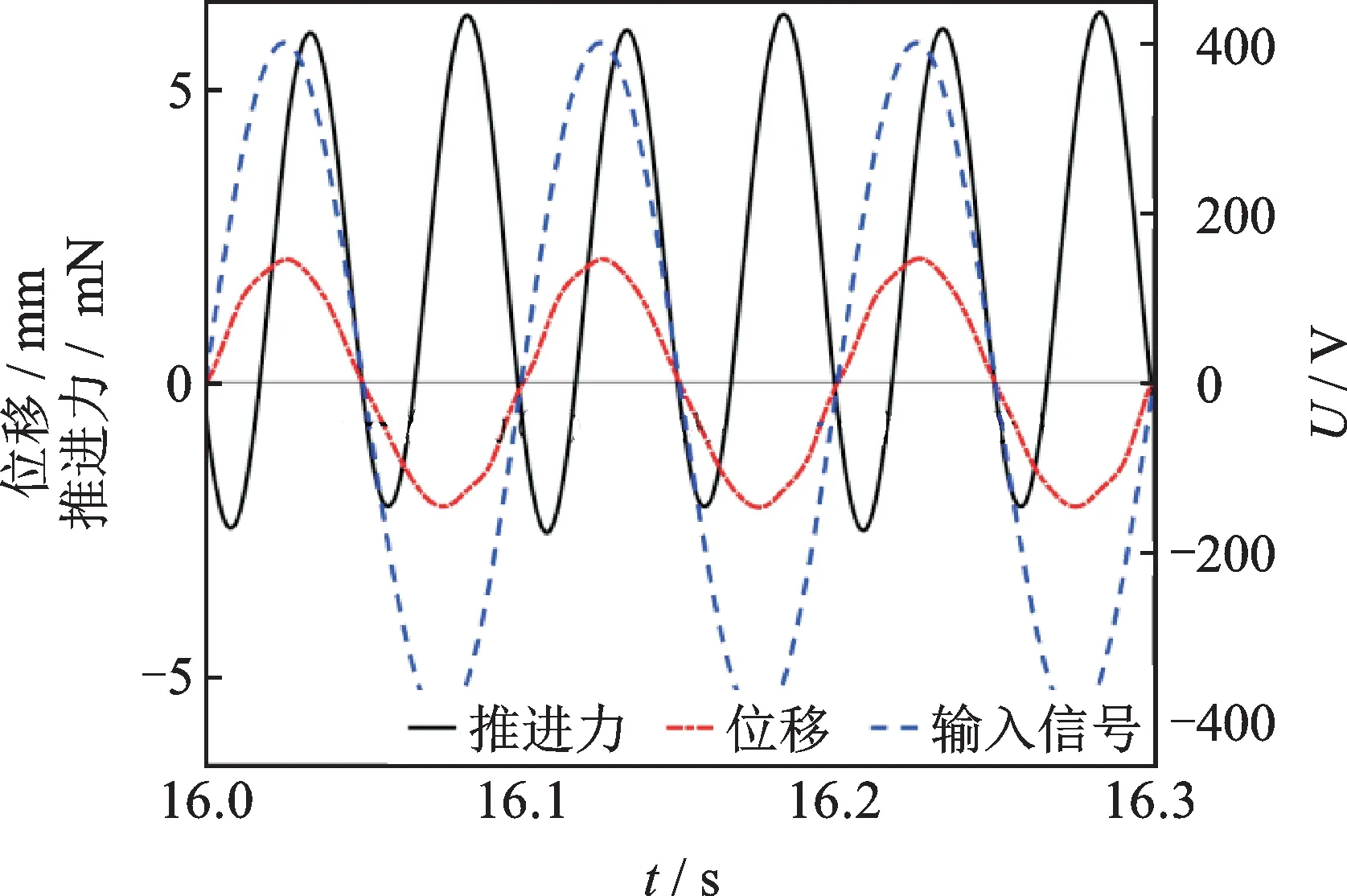
圖11 8 Hz時MFC驅動電壓、尾鰭擺動位移及推進力對比圖Fig.11 Comparisons among the input voltage,oscillation displacement and thrust with the excitation frequency of 8 Hz

為了定量分析柔性仿生尾鰭在MFC驅動下的推進效果，采用數值積分法計算柔性尾鰭在一個擺動周期內的平均推進力，其計算公式為其中：a～b為時間間隔；T為周期；N為等距點的個數；f(x)為推進力曲線。

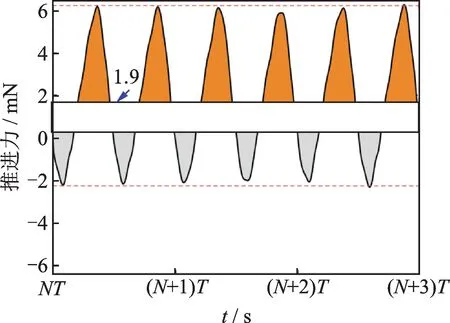
圖12 8 Hz下柔性尾鰭產生的單位周期平均推進力Fig.12 Mean thrust per oscillation period generated by the fin with the excitation frequency of 8 Hz

顯然，式（13）的計算結果就是圖12中橫軸以上推進力曲線圍成的面積（圖中橙色部分）與橫軸以下拖拽力曲線圍成的面積（圖中灰色部分）之差。計算得到柔性仿生尾鰭在最大擺速激勵條件下產生的單位周期平均推進力為1.9 mN。

為了比較不同激勵條件下柔性仿生尾鰭產生的推進力變化情況，研究了柔性仿生尾鰭在獲取最大擺幅峰峰值5.08 mm的激勵條件（激勵頻率為7 Hz，電壓幅值為400 V，激勵時間為20 s）下的推進力變化情況。圖13給出了7 Hz激勵頻率下驅動電壓信號、尾鰭擺動位移以及穩定推進力的對比變化情況。圖14則給出了相應的單位周期平均推進力結果。

類似地，7 Hz激勵頻率下柔性尾鰭產生的推進力在一個穩定擺動周期內出現兩次波峰起伏，且在51.5%的周期內產生推進效果，而在48.5%的周期內起到拖拽作用。產生的瞬時最大推進力和拖拽力分別為5.02和-4.74 mN。數值積分計算得到柔性仿生尾鰭在最大擺幅激勵條件下產生的單位周期平均推進力為0.26 mN。

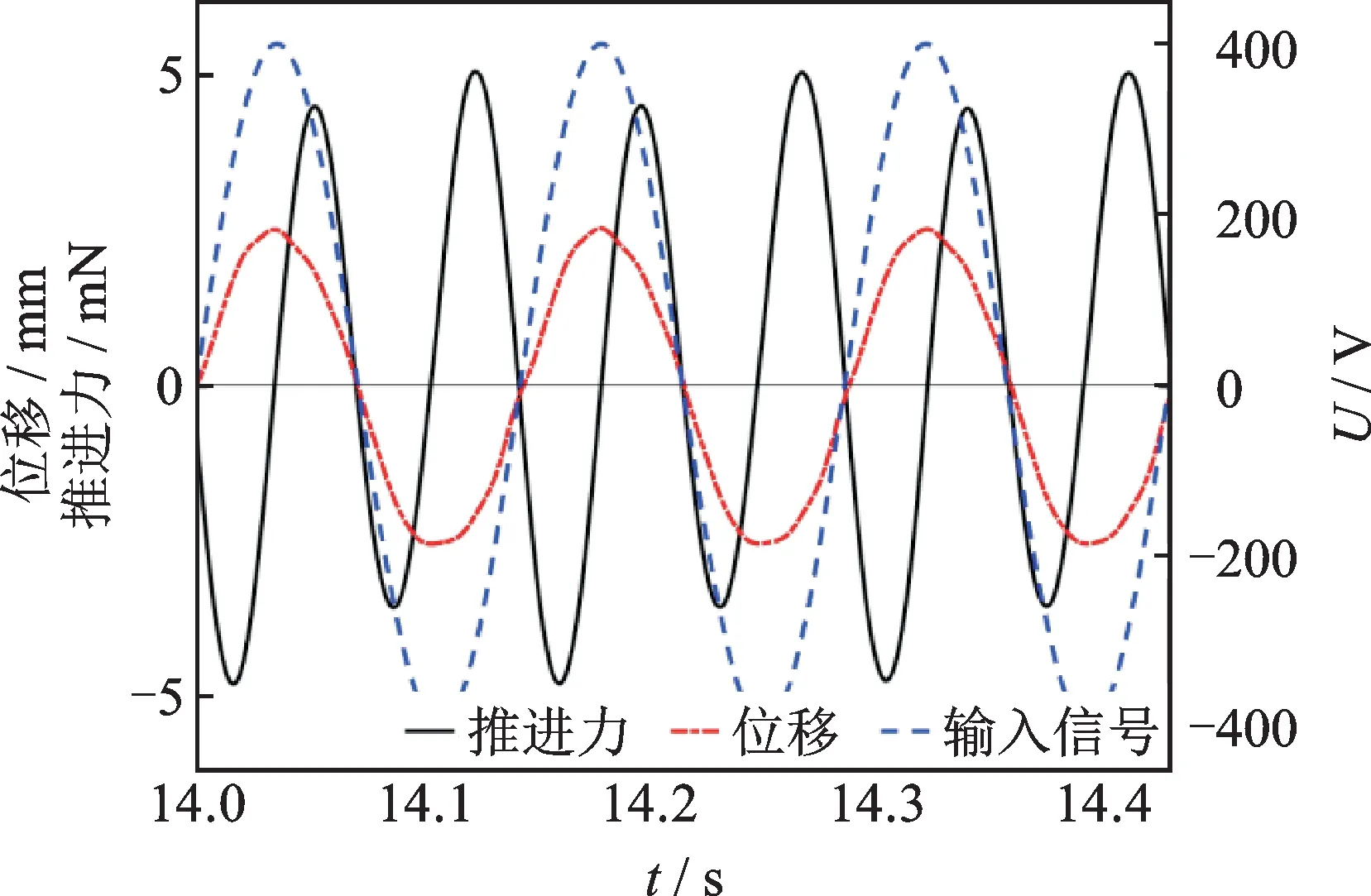
圖13 7 Hz時MFC驅動電壓、尾鰭擺動位移及推進力對比圖Fig 13 Comparisons among the input voltage,oscillation displacement and thrust with the excitation frequency of 7 Hz

圖14 7 Hz下柔性尾鰭產生的單位周期平均推進力Fig.14 Mean thrust per oscillation period generated by the fin with the excitation frequency of 7 Hz

表3 給出了兩種激勵條件下MFC驅動的柔性仿生尾鰭推進性能比較情況。可以看出：柔性尾鰭在取得最大擺速時產生的最大瞬時推進力是最大擺幅激勵條件下的7.3倍；且最大擺速激勵條件下的最大瞬時推進力與拖拽力之比也大于最大擺幅激勵條件的結果。因此，MFC驅動的柔性仿生尾鰭在最大擺速激勵條件下具有更好的推進性能，符合Lighthill的細長體理論。

表3 不同激勵條件下尾鰭推進性能比較Tab.3 Comparisons of thrust performances of the oscillation fin with different excitations mN

5 結束語

筆者分析了MFC驅動的柔性仿錦鯉尾鰭水下擺動過程中的受力情況，提出了用于柔性仿生尾鰭推進力動態精密測量的懸臂式微推進力測量系統，給出了相應的設計指標和計算方法。標定實驗表明懸臂式微推進力測量裝置的實測擬合彎曲剛度與設計指標基本一致。通過測量得到了MFC驅動的柔性仿生尾鰭在不同激勵條件下的推進力動態變化過程。測量結果顯示，仿生尾鰭穩定擺動過程中產生的推進力變化周期是其擺動周期的一半，并存在著推進和拖拽兩種狀態。對比了柔性仿生尾鰭在最大擺幅、最大擺速兩種狀態下產生的瞬時推進力、拖拽力及周期平均推進力結果。本研究給出了一種簡單的微推進器測量系統設計方法，對智能材料驅動的水下仿生推進器的推進性能分析具有一定參考和借鑒作用。