課堂導入要架起“舊知”與“新知”的橋梁

周強

摘要：小學數學的內容是中學數學的基礎，而中學數學的內容則是在小學數學基礎上的延伸與拓展。作為一名中學數學教師，我認識到，在教學過程中，老師要充分發掘教學內容與學生已有的知識與經驗的聯系，根據學生已經掌握的認知規律實施課堂教學，做好中小學數學知識的銜接工作，讓學生從已有的數學知識自然地過渡到中學數學的學習中來，從而為有效的課堂教學打下基礎。

關鍵詞：教學方案? 經驗? 知識銜接

《義務教育數學課程標準（2011年版）》提出“教學方案是教師對教學過程的預設，教學方案的形成依賴于教師對教材的理解、鉆研和再創造”。在七、八年級的數學教學工作中，我們發現有些中學課本中的教學內容在小學階段就已經有過介紹，學生們也有所了解和掌握。這給我們的教學工作帶來了一些困惑：如果按部就班地利用課本內容進行教學，那勢必會讓部分學生感到枯燥，甚至是不耐煩，老師也會感到有些多余，新課導入也會存在困惑。這時，在備課環節上，對中學老師的要求就會提高，老師既要去了解小學數學與初中數學在內容方面有哪些共性與聯系，了解學生已有的知識經驗，又要在此基礎上對教學內容進行有目的的拓展與延伸，對教學方案、課前導入進行有效的創造。

現結合自己的教學工作，從以下幾個課例談起：

一、乘法規律與整式加減

本節課的內容是滬科版數學教材《整式加減》中的“合并同類項”知識點。在備課時，我想到，如果直接從介紹形如a與-7a，1/2xy與-3xy，-6與2等的同類項入手，再去給出同類項的定義，那么學生也是可以理解的。經過思考，學生對同類項的定義的理解與掌握是為了后面學習合并同類項奠定基礎的，于是我想到了小學數學中的乘法運算律——乘法分配律（a+b+c）·m=am+bm+cm，只要將等號左右兩邊的多項式交換一下位置就變為：am+bm+cm=（a+b+c）·m，觀察可得，左邊每一項中都含有因式m，這時可將am，bm，cm看成是同類項，而將a，b，c看成各項前的系數，這不就是合并同類項嗎？合并同類項的規則也就更明了了。

于是，這節課我從簡便計算算式：23×3.14-3.14×7-6×3.14入手，讓學生利用已有的經驗快速地計算結果，學生利用小學已學的乘法分配律便可以進行簡便計算。接著我再追問如果將算式中的3.14變為ab或x2y，即23ab-7ab-6ab或23x2y-7yx2-6x2y（將第二項這樣寫是為了考查學生的觀察能力）能否快速算出結果，學生們也能輕松說出答案。最后我讓同學們去觀察這兩個多項式中的每一項有怎樣的聯系，此時，他們發現了式子中每一項的特點，并歸納出了同類項的定義。

此例通過學生掌握的小學數學運算律，為中學課堂中的新知導入創設了情境，做了較好的鋪墊，讓學生感到不陌生，過渡自然，學生能較為容易地進行理解、掌握及運用。

二、乘法運算與整式乘法

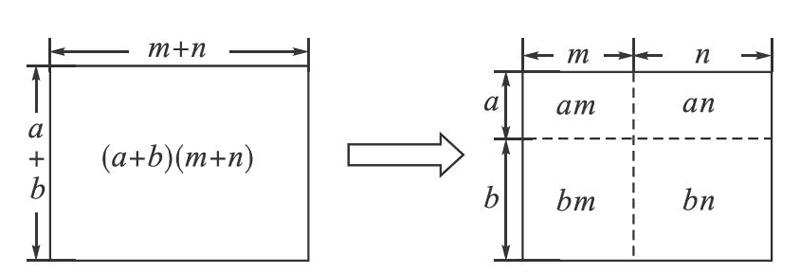
本節課的內容是滬科版數學教材《整式乘除與因式分解》中的《多項式乘以多項式》一節。備課時，我通過整體與部分的思想，利用計算圖形面積的方法去歸納，總結得出多項式乘以多項式的運算法則，這也是中學數學中經常強調的數形結合的思想，即（a+b）（m+n）的結果可以看成是求邊長分別為（a+b）與（m+n）的長方形的面積，如圖所示：

通過將邊長分別為（a+b）與（m+n）的長方形分為四個獨立的小長方形，并分別求出它們各自的面積，根據圖形在分割前與分割后面積相等的等量關系，我們便總結、歸納出多項式乘以多項式的運算法則，即（a+b）（m+n）=am+an+bm+bn。

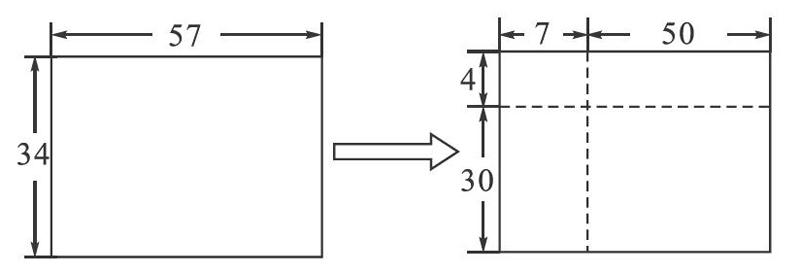
如果把上述的知識與小學中學習的乘法運算相聯系，如計算34×57，其運算結果便可以看成是求邊長分別為34與57個單位長度的長方形的面積，再利用與上面相類似的分解方法，將34分解成（4+30），57分解成（7+50）。

將圖形進行分解后的四個小長方形的面積分別為：4×7=28;4×50=200;30×7=210;30×50=1500。只要將上述運算的四個結果加在一起就可以得出邊長分別為34與57個單位長度的長方形的面積，即34×57=4×7+4×50+30×7+30×50的結果。

這類問題從安排上來看，是中學知識依托在小學知識的基礎上。在小學數學中，把兩數的乘法運算通過數形結合的思想來進行教學是具有一定的難度，但對學生思維能力的拓展是十分有利的。數形結合的思想是初中數學學習中的一個重要的知識點，在教學過程中，通過先設置計算兩數的積的數形結合的情境，再由一般到特殊，轉換為兩多項式的乘積，會讓學生更加容易地理解和運用。

三、三角形內角和

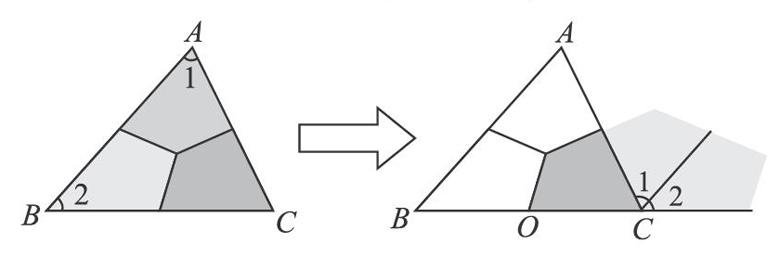
本節內容是滬科版數學教材《三角形中的邊角關系、命題與證明》中的《命題與證明》的第二課時，三角形內角和的教學內容，對小學數學與中學數學而言都是十分重要的組成部分。在中學數學的課堂教學中，學生對“三角形內角和為180°”的結論記憶深刻，在小學階段，學生們通過量角器測量度數，折紙拼接成平角，這種根據觀察、實驗的結果，大膽猜想三角形內角和為180°，讓學生在原有知識的基礎上參與其中，既改善了學生的學習方式，也調動了學生學習的積極性。

在初中階段，三角形內角和為180°是通過演繹推理證明的方法得出的。相比于小學數學所得結論的過程，是嚴謹合理的，由于在小學階段得出過相同的結論，所以學生在課堂上會感覺到枯燥無味，缺乏學習熱情，學生更多的時候是在配合老師上課。

于是課堂上我借助于幾何畫板動態演示學生們在小學進行過的操作，將三個內角拼接成一個角，同時計算三角形三個內角∠1+∠2+∠ACB的和，這與變換后組合成的平角一致。這時學生會對已有的知識重新煥發學習的熱情。之后嚴格的推理證明也就水到渠成了。

從以上三個課例中可以看出，如果僅僅基于中學數學課本進行教學，那會造成與小學數學在知識銜接上的脫節。這也就說明了為什么小學生剛上了中學后，會有一段時間感到不適應。除了因為中學數學的知識點較多，難度較大，教學進度較快之外，與小學的教學方法是強調直觀演示，偏重形象思維，而中學的教學方法是強調推理論證，偏重抽象思維是分不開的。作為中學教師，我們在研究和選擇教學方法時，要去尋找學生已經掌握的知識點，讓教學的過程順暢一些，知識的銜接緊密一些，問題的坡度小一些，讓學生能夠在熟悉的情境中去獲得新知，感受成功帶來的喜悅與歡樂。這便要求中學教師熟悉中小學數學知識在教學內容上的聯系，注重采取學生已了解、已掌握的知識點去導入新課，為學生架起“舊知”與“新知”的橋梁。

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2]夏永立.數學課堂教學探索[M].合肥：安徽科學技術出版社，2017.