面向類不平衡網(wǎng)絡(luò)流量的特征選擇算法

唐 宏 劉 丹* 姚立霜 王云鋒 裴作飛

①(重慶郵電大學(xué)通信與信息工程學(xué)院 重慶 400065)

②(移動通信技術(shù)重慶市重點實驗室 重慶 400065)

1 引言

網(wǎng)絡(luò)流量分類技術(shù)廣泛應(yīng)用于網(wǎng)絡(luò)管理和網(wǎng)絡(luò)安全領(lǐng)域[1]。基于端口號的流量分類方法[2,3]在開放端口、偽裝端口號等技術(shù)出現(xiàn)之后，分類準確率大大降低。基于特征字段的流量分類方法擺脫了對端口號的依賴，可以取得較高的分類準確率，但該方法只能對明文傳輸?shù)臄?shù)據(jù)包進行解析，難以適用于加密流量的分類[4-6]。基于傳輸層主機行為的流量分類方法不依賴于端口號，也不需要解析報文，但該方法對外界環(huán)境異常敏感，多變的網(wǎng)絡(luò)環(huán)境可能導(dǎo)致分類效果不夠穩(wěn)定。因此，基于機器學(xué)習的網(wǎng)絡(luò)流量分類方法得到了研究人員的青睞[1,7]。

數(shù)據(jù)預(yù)處理是基于機器學(xué)習的網(wǎng)絡(luò)流量分類過程中的重要步驟，該過程通常采用特征選擇算法對特征進行降維。Moore等人[8]使用快速相關(guān)濾波器去除冗余和無關(guān)的特征。Dai等人[9]利用卡方和C4.5算法進行特征選擇。Xu等人[10]將二進制螢火蟲算法與反向?qū)W習相結(jié)合進行特征選擇。張震等人[11]通過定義基于信息熵的“用戶行為模式”來分析各個行為子簇背后表現(xiàn)出的業(yè)務(wù)特征，能有效降低算法的計算復(fù)雜度。Shafiq等人[12]提出了一種基于機器學(xué)習的混合特征選擇算法，該算法利用了加權(quán)互信息度量和受試者工作特征曲線(Receiver Operating Characteristic, ROC)下面積兩個指標，使用該算法選擇出的特征能夠表現(xiàn)出很好的性能。Shi等人[13]提出了一種新的基于深度學(xué)習和特征選擇技術(shù)的特征優(yōu)化方法，為流量分類提供具有強區(qū)分能力的特征。Wang等人[14]提出一種基于多重過濾權(quán)重和多重特征權(quán)重的混合特征選擇方法，能有效提高分類精度。王勇等人[15]在特征提取過程中引入卷積神經(jīng)網(wǎng)絡(luò)，可以在避免復(fù)雜顯式特征提取的同時達到提高分類精度的效果。Ren等人[16]使用深層神經(jīng)網(wǎng)絡(luò)挑選數(shù)據(jù)的固有特征，利用樹結(jié)構(gòu)的遞歸神經(jīng)網(wǎng)絡(luò)處理大規(guī)模流量分類問題，可以在更少的訓(xùn)練時間內(nèi)獲得更高的性能。

現(xiàn)有的特征選擇算法多數(shù)情況下選擇出來的特征在多數(shù)類(大類)上表現(xiàn)良好，分類器對少數(shù)類(小類)的預(yù)測精度卻很低，這就是類不平衡導(dǎo)致的問題。然而，在現(xiàn)實生活中，人們通常更關(guān)注小類的分類效果，錯誤地識別小類所帶來的后果往往很嚴重。如在入侵檢測中[17-19]，攻擊類相對于正常流量就屬于小類，錯分攻擊類可能會引起網(wǎng)絡(luò)的癱瘓。

為了減輕類不平衡問題帶來的不良影響，本文提出一種基于加權(quán)對稱不確定性(Weighted Symmetric Uncertainty, WSU)和近似馬爾科夫毯(Approximate Markov Blanket, AMB)的網(wǎng)絡(luò)流量特征選擇算法。該算法首先根據(jù)類別分布信息定義偏向于小類別的度量，使得識別小類別的特征更容易被選擇出來，并基于加權(quán)信息熵計算特征與類別間的加權(quán)對稱不確定性，利用特征排序算法刪除不相關(guān)特征；然后，充分考慮特征與類別間、特征與特征間的相關(guān)性，利用近似馬爾科夫毯條件刪除冗余特征；最后，根據(jù)特征評估準則函數(shù)和序列搜索算法從候選特征集合中選出滿足合適維數(shù)的特征子集。

2 特征選擇

特征選擇的流程圖如圖1所示，它主要包含4個基本環(huán)節(jié)：生成特征子集(搜索策略)，評價準則，停止準則和結(jié)果驗證[20]。在原始特征集上運用搜索策略得到生成子集，利用評價準則對第1步選擇出來的子集進行評估，最后根據(jù)停止準則結(jié)束搜索，并選擇出來的最優(yōu)特征子集進行檢驗，判斷所選特征子集是否滿足標準。

3 基于WSU_AMB的特征選擇算法

基于加權(quán)對稱不確定性和近似馬爾科夫毯(WSU_AMB)的網(wǎng)絡(luò)流量特征選擇算法主要包含兩個步驟。第1步，根據(jù)類別分布信息定義偏向于小類別的權(quán)值，基于加權(quán)信息熵計算出特征與類別間的加權(quán)對稱不確定性，利用特征排序算法刪除不相關(guān)特征，這一步可以過濾掉大多數(shù)特征；計算特征與特征之間的加權(quán)對稱不確定性，利用近似馬爾科夫毯刪除冗余特征，確定候選特征集合。第2步，計算特征準則評估函數(shù)值，利用序列搜索算法選擇出滿足合適維度的特征子集。WSU_AMB算法的總體框架如圖2所示。

3.1 加權(quán)對稱不確定性

加權(quán)對稱不確定性可以用來衡量特征與類別以及特征與特征之間的相關(guān)性，它是在加權(quán)信息熵的基礎(chǔ)上計算出來的[21]。加權(quán)對稱不確定性可由式(1)進行計算

其中

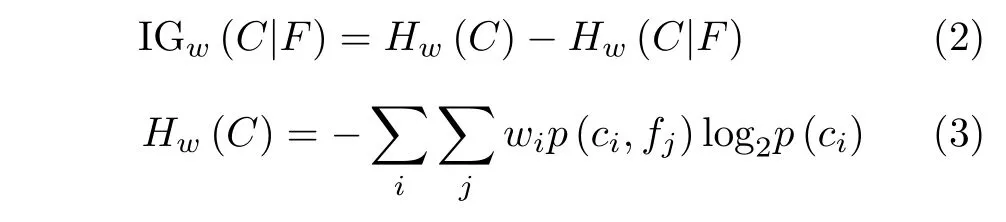
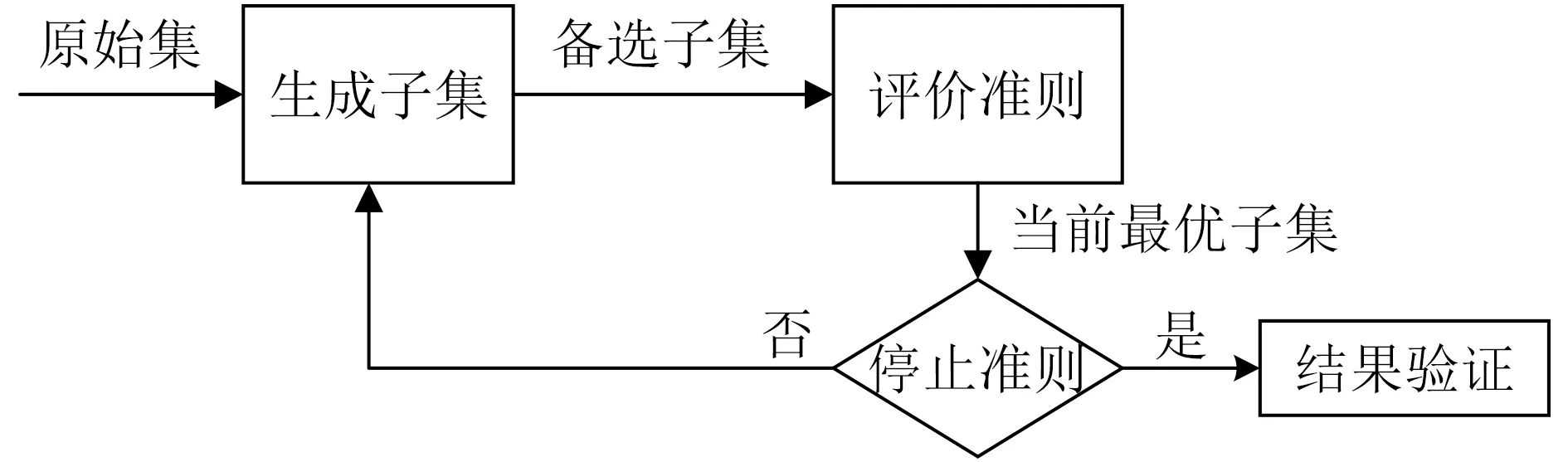
圖1 特征選擇流程圖

圖2 WSU_AMB特征選擇算法的總體框架

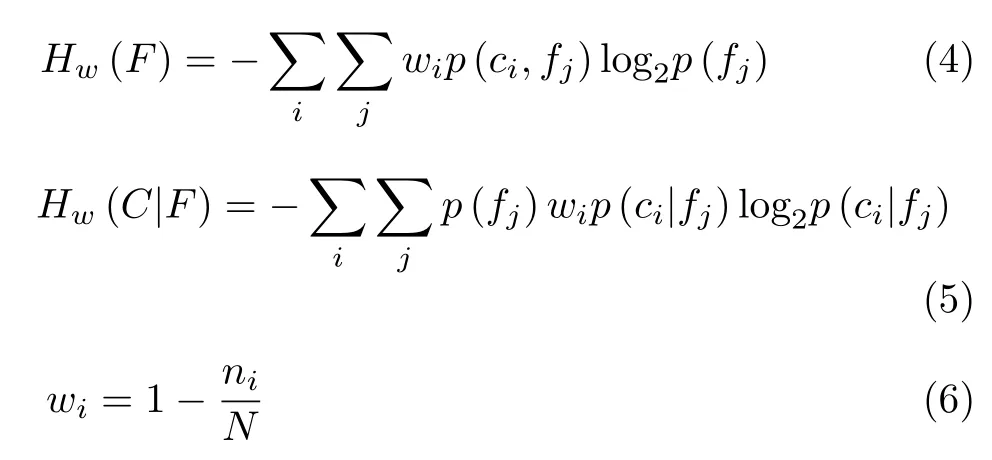
wi表 示權(quán)值，p (ci,fj)表示類別C與特征F的聯(lián)合概率， p(ci) 表示類別C的先驗概率，p (fj)表示特征F的先驗概率， p (ci|fj)表示F發(fā)生的條件下C的后驗概率， ni表示屬于類別ci的樣本數(shù)，N表示樣本總量。

通過加權(quán)對稱不確定性，可對相關(guān)特征進行定義，具體表述為：計算每個特征與類別之間的加權(quán)對稱不確定性W SU(fi,C)，對該值進行降序排列，排在最前面、值越大所對應(yīng)的特征與類別的相關(guān)性越 強。

3.2 近似馬爾科夫毯

通常對特征與特征之間的相關(guān)性進行分析來判定某一特征是否冗余。根據(jù)馬爾科夫毯思想可以形式化地給出冗余特征的定義，但是馬爾科夫毯的條件過于嚴格，現(xiàn)實數(shù)據(jù)難以達到要求，需要對該條件進行近似假設(shè)[22]，基于此，本節(jié)提出了近似馬爾科夫毯來刪除冗余特征。

所謂馬爾科夫毯，需滿足以下條件。假設(shè)屬性類別為C，特征集合為F，對于給定的特征fi?F和特征子集M ?F(fi∈/M)，若有

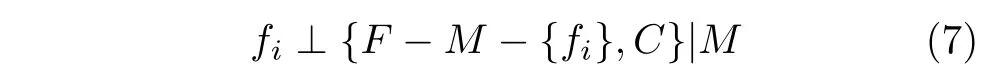
則稱能滿足上述條件的特征子集M為fi的馬爾科夫毯。其中，符號“⊥”表示獨立，“|M”表示在給定M的條件下。

假設(shè)屬性類別為C，特征集合為F，特征 fi為冗余特征的充要條件為當且僅當存在特征子集M為fi的馬爾科夫毯，其中，fi?F , M ?F(fi∈/M)。在特征集合F中，由于在特征 fi的馬爾科夫毯M條件下，fi與其他非馬爾科夫毯變量獨立，因此，對于特征 fi而言，所有非馬爾科夫毯變量都是冗余的。

特征 fi是特征fj的 近似馬爾科夫毯( i/=j)，需要滿足式(8)的條件

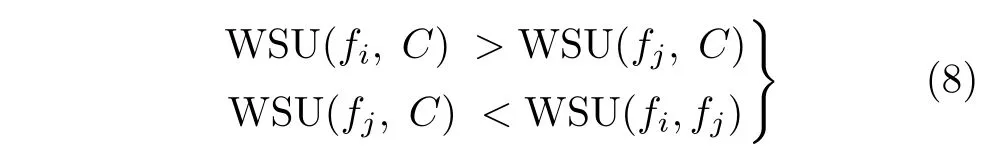
特征與類別之間的WSU可由式(5)得到，特征與特征之間的WSU的計算方法略有差別，此時需要 將其中一個特征看成類別屬性。

3.3 相關(guān)性特征度量

在充分考慮特征的相關(guān)性的前提下，有效減少特征維數(shù)，提出一種特征準則評估函數(shù)

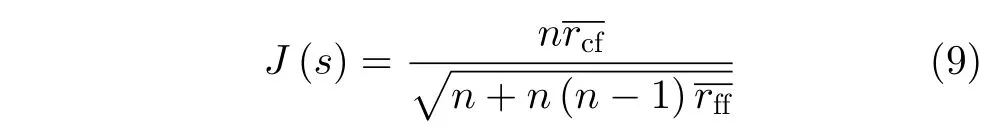
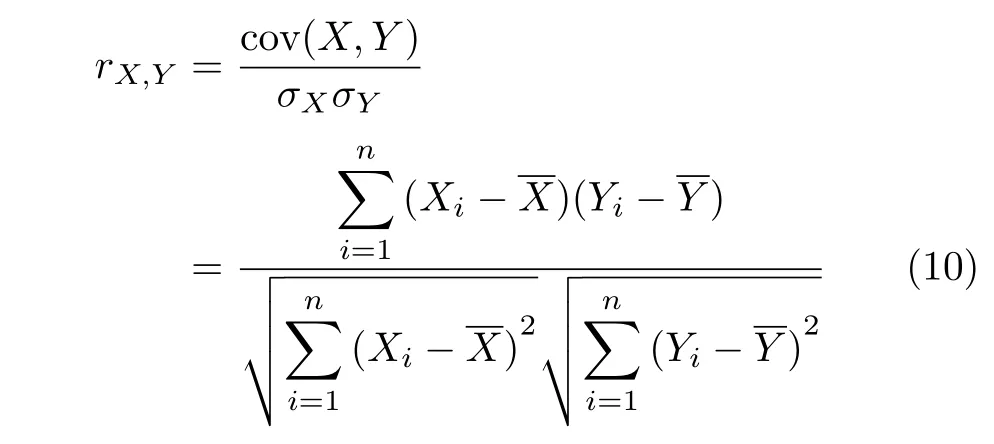
3.4 算法流程描述

WSU_AMB算法的實現(xiàn)過程如表1所示。第1階段((1)～(9)行)利用加權(quán)對稱不確定性和近似馬爾科夫毯條件刪除不相關(guān)特征和冗余特征，得到候選特征集合；第2階段((10)～(20)行)利用特征評估準則函數(shù)和序列搜索算法找到最優(yōu)特征子集。

4 實驗驗證

4.1 實驗數(shù)據(jù)集

本實驗使用Moore數(shù)據(jù)集[23]來驗證算法的性能，表2展示了該數(shù)據(jù)集的統(tǒng)計信息。

4.2 性能評價指標

本實驗采用整體精確率(accuracy)，小類別的準確率(precision)、召回率(recall)和F1值作為算法的性能評價指標。整體精確率可以反映多分類模型的綜合預(yù)測能力，準確率、召回率和F1值可以反映分類模型對單個應(yīng)用的預(yù)測能力。

4.3 實驗方案

利用Moore數(shù)據(jù)集的10個數(shù)據(jù)子集(DataSet1,DataSet2, ···, DataSet10)進行訓(xùn)練和預(yù)測，每個子集中訓(xùn)練集的比例為70%。選用C4.5決策樹作為分類器進行所提算法的最優(yōu)參數(shù)選擇。

在對網(wǎng)絡(luò)流量進行分類時，一般4～8個特征就能得到較好的分類效果。本文對10個數(shù)據(jù)子集進行實驗，可以發(fā)現(xiàn)相似的變化趨勢，只選取2個數(shù)據(jù)子集進行展示，如圖3，經(jīng)驗證，選取特征數(shù)L=6。

閾值δ的設(shè)置對算法的性能有重要影響。因為δ值越高，篩選特征的速度越快，但會遺漏某些重要特征，降低分類系統(tǒng)的性能；δ值越低，會把訓(xùn)練樣本自身的某些特點當成共性來學(xué)習，會導(dǎo)致分類器泛化性能下降，出現(xiàn)“過擬合”的現(xiàn)象。同樣地，利用10個數(shù)據(jù)子集進行閾值選擇實驗，分類器的整體精確率變化趨勢相似，如圖4所示，本文選取了2個數(shù)據(jù)子集進行實驗展示。通過實驗驗證，選取閾值δ=0.55。

表1 基于WSU_AMB的特征選擇算法

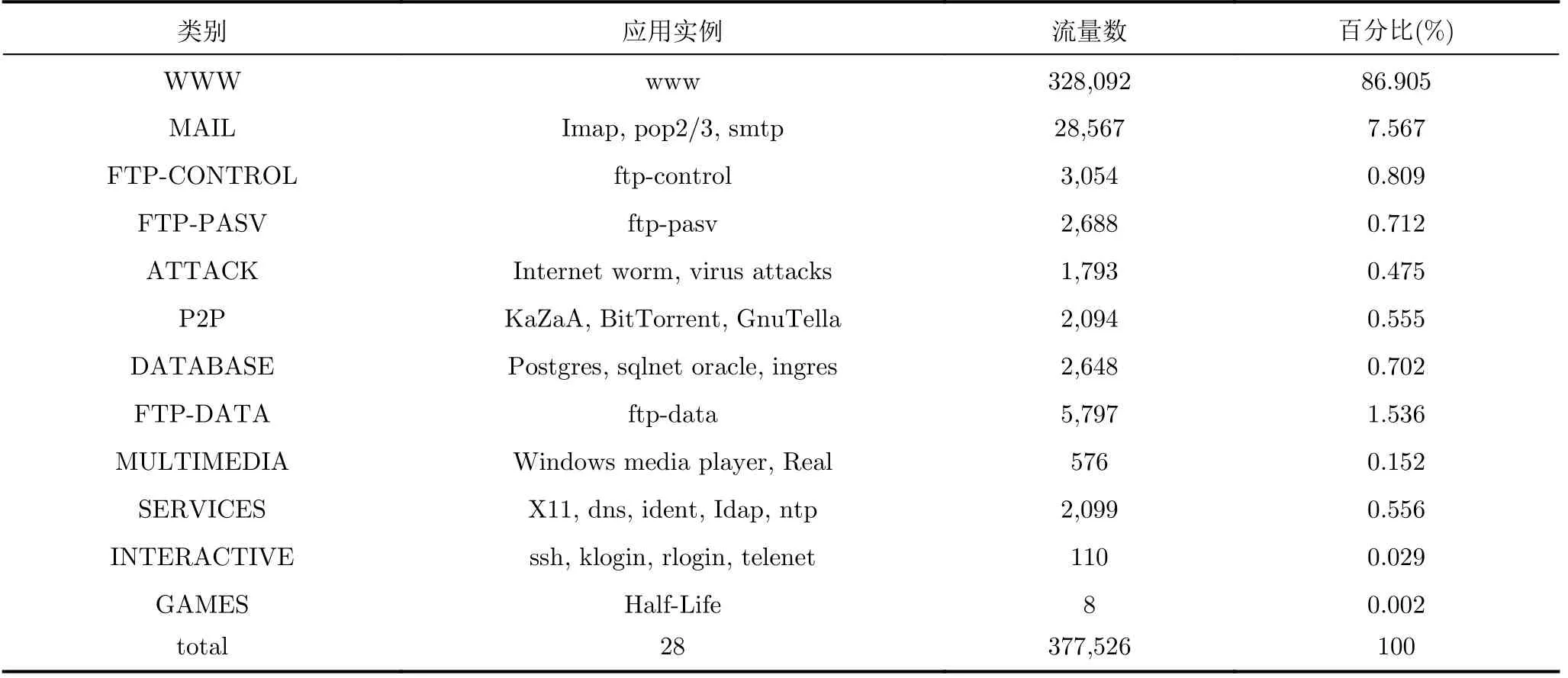
表2 Moore數(shù)據(jù)集的統(tǒng)計信息

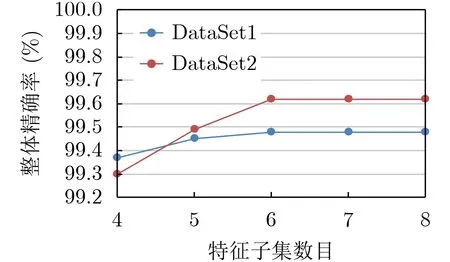
圖3 特征子集數(shù)目L對算法的影響

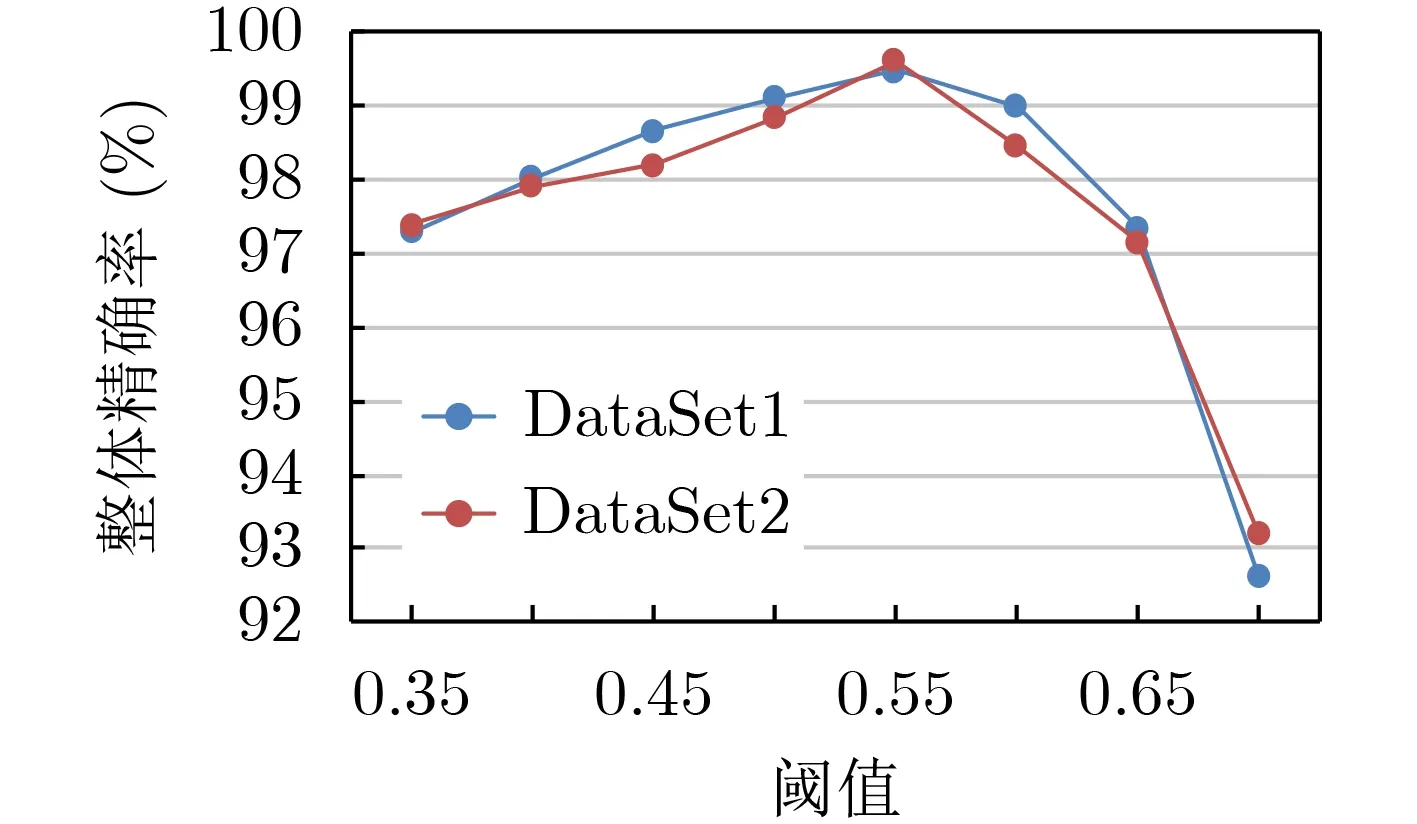
圖4 閾值δ對算法的影響

在實驗過程中，利用4種分類器：樸素貝葉斯(Naive Bayes, NB)、邏輯斯蒂回歸模型(Logistic Regression, LR)、K近鄰算法(K-Nearest Neighbour,KNN)和C4.5決策樹(Decision Tree, DT)，將未進行特征選擇的數(shù)據(jù)集(fullset)、基于相關(guān)的快速過濾器(Fast Correlation-Based Filter, FCBF)[8]、卡方?jīng)Q策樹算法(Chi-Square and Decision Tree,CSDT)[9]、高效的特征優(yōu)化方法(Efficient Feature Optimization Approach, EFOA)[13]以及基于多重過濾權(quán)重和多重特征權(quán)重的混合特征選擇方法(Hybrid Feature Selection based on Multi-Filter weights and Multi-Feature weights, MFHFS)[14]與所提算法(WSU_AMB)進行對比。

4.4 實驗結(jié)果與分析

4.4.1 所選特征集合

選用C4.5決策樹作為分類器，在不同的數(shù)據(jù)子集下，F(xiàn)CBF, CSDT, EFOA, MFHFS和WSU_AMB算法選擇出來的特征數(shù)目如表3所示。選出的特征子集規(guī)模顯示，總體上WSU_AMB算法所選特征數(shù)較少，CSDT算法所選的特征數(shù)較多，其他3種算法的降維能力相當。WSU_AMB算法的停止準則是基于搜索策略設(shè)定的，一旦所選特征達到指定個數(shù)即停止搜索，所以在不同的數(shù)據(jù)子集上，WSU_AMB算法選擇的特征個數(shù)都相同。而其他4種算法的停止準則是基于評價準則設(shè)定的，需要在評價價值達到最高時才停止搜索，故每個數(shù)據(jù)子集所選特征個數(shù)會有所不同。

4.4.2 算法復(fù)雜度對比

表4對各算法的時間復(fù)雜度進行了定性分析，其中，N為特征總數(shù)，M為數(shù)據(jù)集的實例數(shù)目，L為候選特征集合中的特征數(shù)量，D為隱層數(shù)，t為當前所在的層，Nt為 該層的特征數(shù)，Ct為該層的類別數(shù)，K為選擇的特征數(shù)。

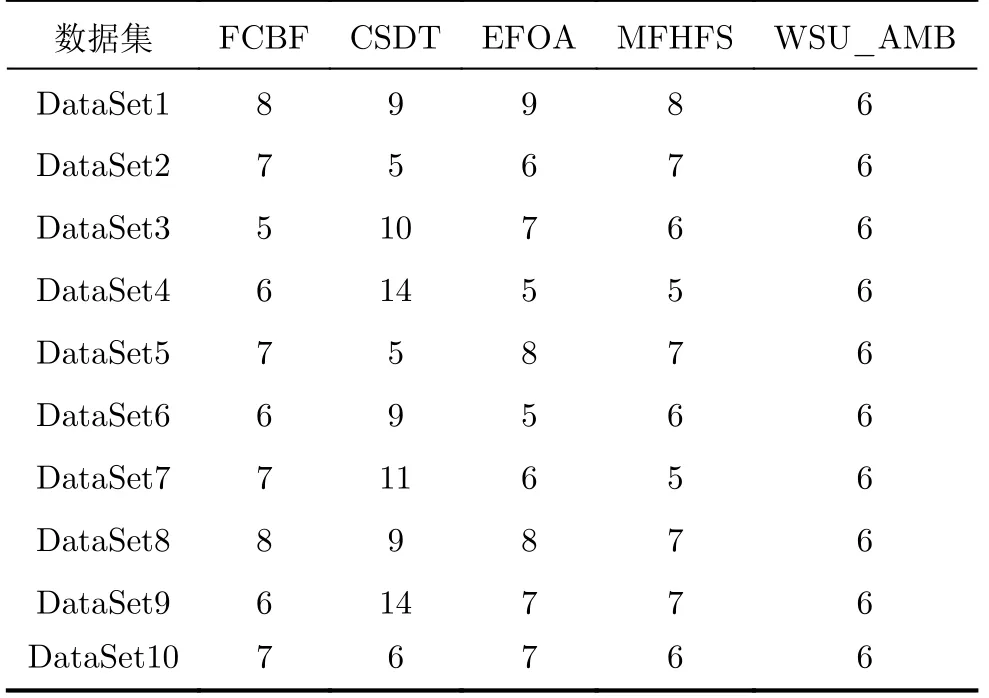
表3 不同特征選擇方法所選特征數(shù)目

表4 不同特征選擇方法的時間復(fù)雜度分析

為了進一步對算法的復(fù)雜度進行定量分析，利用Moore數(shù)據(jù)集的10個特征子集對各算法的特征選擇時間進行統(tǒng)計，如圖5所示。從圖5中可看出算法運行時間與算法復(fù)雜度的定性分析基本保持一致，WSU_AMB算法的特征選擇時間少于EFOA算法，MFHFS算法的特征選擇時間最短；因DataSet7～DataSet10的數(shù)據(jù)量較大，是前6個數(shù)據(jù)子集的2倍多，故EFOA算法的特征選擇時間出現(xiàn)了明顯的增長。

同時，選用C4.5決策樹作為分類器，對各算法的分類時間進行了測試，如表5所示。很明顯，使用基于CSDT算法和EFOA算法選擇出來的特征進行C4.5分類器的訓(xùn)練，分類時間較長，而C4.5使用WSU_AMB算法選擇出來的特征進行分類時，分類速度優(yōu)于FCBF算法和MFHFS算法。雖然WSU_AMB算法在特征選擇階段的運行時間較長，但經(jīng)過特征選擇之后所選特征的特征值數(shù)目較小、數(shù)量較少，減少了分類過程中的計算開銷，縮短了系統(tǒng)在分類階段的耗時，提升了系統(tǒng)的分類效率。

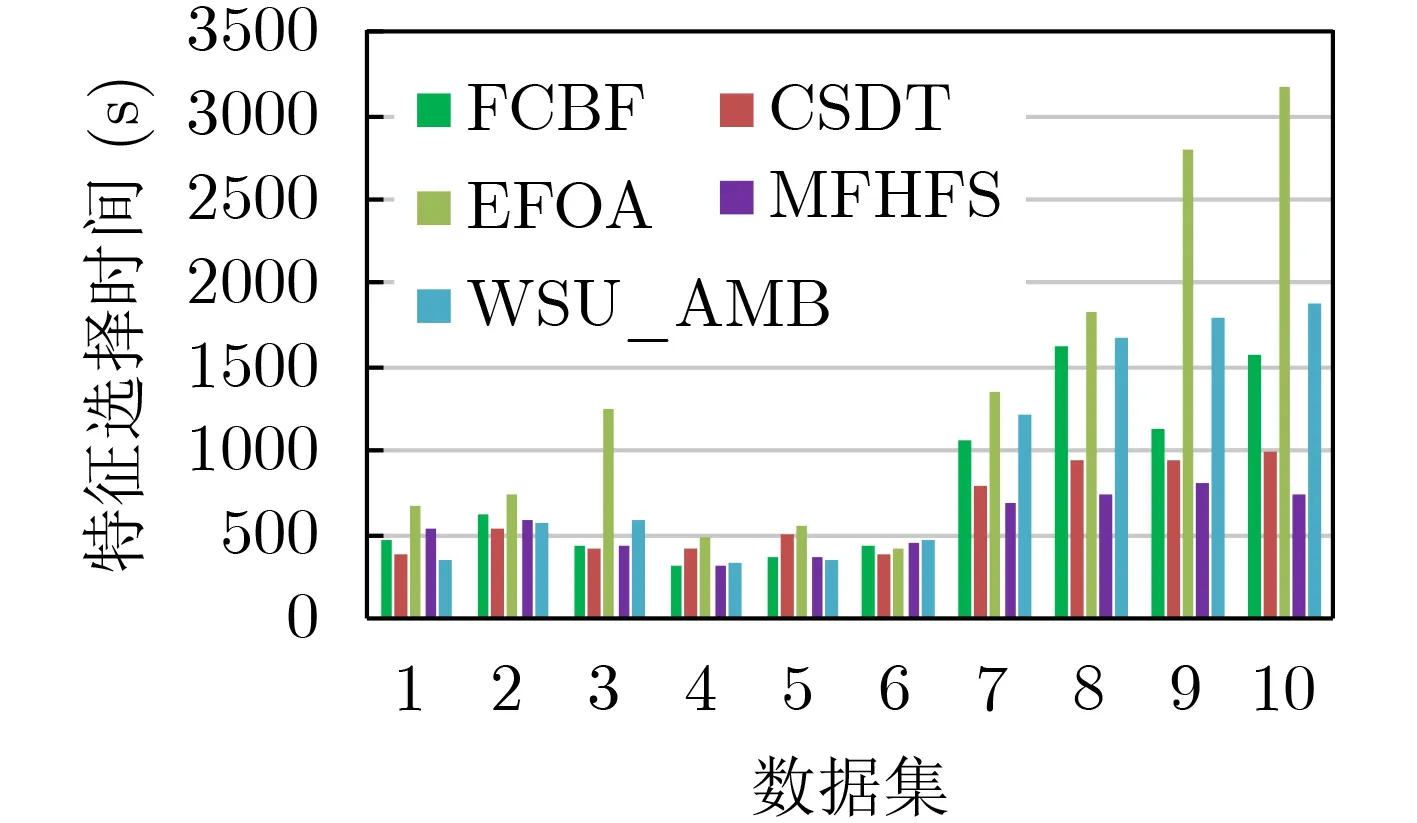
圖5 不同算法在各數(shù)據(jù)集上的特征選擇時間對比

4.4.3 分類性能對比

(1) 整體分類精確率。按照4.3節(jié)的實驗方案進行實驗，可以得到各特征選擇算法在不同數(shù)據(jù)子集上的整體精確率。如圖6所示，當NB, LR, 6NN和DT作為分類器時，WSU_AMB算法的平均整體精確率均高于對比算法。使用6NN作為分類器時，各特征選擇算法的分類性能更加穩(wěn)定，當使用DT分類器時，5種特征選擇算法均能取得較高的整體分類準確率。

表5 分類時間的比較(ms)

(2) 小類準確率。選擇ATTACK類和FTPPASV類對5種特征選擇方法在小類別上的性能進行分析。圖7為基于不同數(shù)據(jù)子集，5種特征選擇算法在DT分類器上的小類準確率對比。相比FTPPASV類，ATTACK類在各個數(shù)據(jù)子集上的波動比較大。因為ATTACK類屬于攻擊類型，它通常會模仿其他流量的特征來躲避網(wǎng)絡(luò)監(jiān)測系統(tǒng)，故ATTACK類的分類結(jié)果呈現(xiàn)不穩(wěn)定的特性。相比于其他4種對比算法，WSU_AMB算法對ATTACK類和FTP-PASV類的準確率提升明顯，MFHFS算法的小類準確率性能僅次于WSU_AMB算法。

圖6 不同數(shù)據(jù)子集下各特征選擇算法在4種分類器上的整體精確率對比

圖7 各特征選擇算法的小類準確率對比

(3) 小類召回率。由于網(wǎng)絡(luò)流量中的WWW類占絕大多數(shù)，所以在訓(xùn)練分類器時，往往對WWW類有利，容易把其他類別錯分為WWW類，降低小類別的分類性能。而WSU_AMB算法為小類別選擇出強相關(guān)性的特征，能夠有效減少小類別被錯分為WWW類的數(shù)量，提高小類別的召回率。圖8為使用DT分類器，5種算法在各個子集上的小類召回率，可以看出，WSU_AMB算法的小類召回率好于對比算法。

(4) 小類F1值。圖9為基于不同數(shù)據(jù)子集，5種特征選擇算法在DT分類器上的小類F1值對比。WSU_AMB算法在對每個特征進行度量時，識別小類別的特征權(quán)重更大；在對特征進行選擇時，保證所選的特征具有較強的區(qū)分能力，即特征與類別之間高度相關(guān)，特征之間彼此不相關(guān)。因此，WSU_AMB算法的小類平均F1值能夠高于其他4種方法。

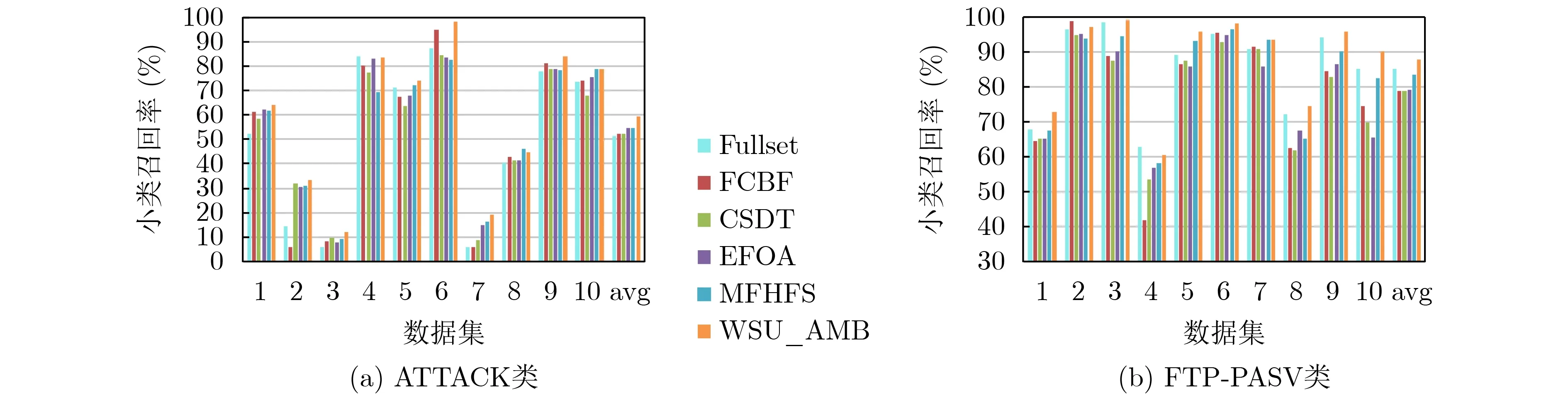
圖8 各特征選擇算法的小類召回率對比

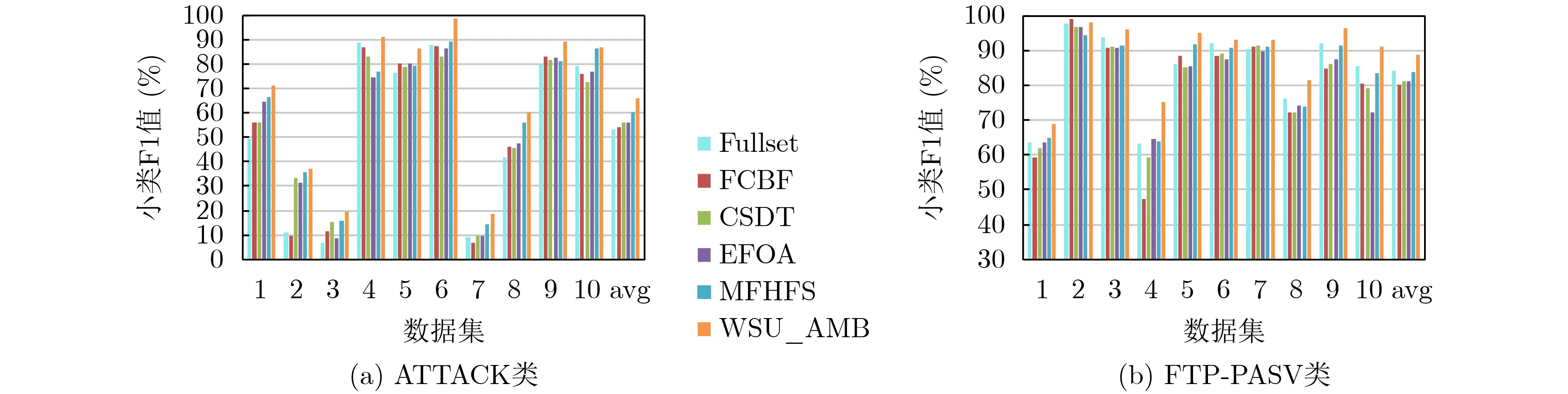
圖9 各特征選擇算法的小類F1值對比

5 結(jié)束語

針對網(wǎng)絡(luò)流量分類技術(shù)存在的類不平衡問題，本文提出一種基于加權(quán)對稱不確性和近似馬爾科夫毯的特征選擇算法。充分考慮特征的相關(guān)性，利用偏向于小類別的加權(quán)對稱不確性和特征排序算法來濾除不相關(guān)特征，通過近似馬爾科夫毯條件刪除冗余特征；再根據(jù)特征評估準則函數(shù)和序列搜索算法進一步降低特征維數(shù)。實驗表明，服務(wù)器的端口號和初始窗口中發(fā)送的字節(jié)總數(shù)是識別網(wǎng)絡(luò)流量的兩個重要特征，所提算法能夠在不犧牲分類器整體精確率的前提下，有效提高小類別的準確率、召回率和F1值。進一步研究工作主要在以下幾個方面：(1)減小數(shù)據(jù)漂移現(xiàn)象的影響；(2)有效降低算法在搜索最優(yōu)特征子集時的時間消耗；(3)新應(yīng)用的識別與分類。