K頻段斐波那契網(wǎng)格稀疏陣列分析與設計*

溫 劍，陽 昆，姚亞利，侯祿平

(中國西南電子技術研究所，成都 610036)

0 引 言

在國內外近年來蓬勃發(fā)展的K/Ka頻段(大約20～30 GHz，非嚴格定義)低軌衛(wèi)星通信網(wǎng)絡有源相控陣天線領域，由于衛(wèi)星軌道高度較低(1 000 km左右)，要求采用高增益波束寬角掃描(≥±60°)形成對地球覆蓋。采用均勻網(wǎng)格排布(矩形、正方形、三角形)的常規(guī)陣列受到柵瓣條件的嚴格限制，其陣間距接近半波長。而目前國內受射頻芯片技術的限制，在高成本高可靠性的衛(wèi)星平臺上仍主要采用具有高輸出功率、低噪聲系數(shù)、抗輻照特性的砷化鎵(GaAs)芯片，但GaAs工藝集成度不高，射頻芯片尺寸與陣間距相當。另外衛(wèi)星平臺資源緊缺，對K/Ka頻段相控陣天線提出多波束、多功能化的要求，常規(guī)陣列難以在5～8 mm的間距下排布多波束芯片及合成網(wǎng)絡。K/Ka頻段常規(guī)陣列電路布局設計和加工制造帶來非常大的困難，嚴重制約了K/Ka頻段衛(wèi)星通信有源相控陣天線向多波束、低剖面、數(shù)字化、低成本化發(fā)展，工程中對陣列大間距稀疏設計提出了迫切的需求。

K/Ka頻段有源相控陣高密度的電路、芯片集成，也要求稀疏陣列網(wǎng)格具有宏觀上的均勻性，便于陣元與芯片位置匹配。K/Ka頻段通信大瞬時帶寬要求各射頻通道長度差異小，盡量減少高成本高損耗的延時器的使用。在稀疏陣布局設計時應全局考慮以上通信用有源相控陣的特殊要求。

滿陣的副瓣和柵瓣是由于陣元的周期排布形成的。稀疏陣設計的核心，就是采用密度加權(規(guī)則網(wǎng)格點隨機采樣)、位置隨機等手段破壞周期性，達到降低副瓣峰值、抑制柵瓣的效果，同時保證增益等核心指標達到門限值。工程中常采用遺傳算法、粒子群算法等全局優(yōu)化算法尋找的最佳的隨機陣列分布，由于沒有明顯的數(shù)學物理對應關系，導致在設計陣元數(shù)超過幾百的大規(guī)模陣列時，未知量大、計算量大、收斂慢[1-4]。為了減少計算未知量常常對陣列做簡化，如子陣塊隨機布陣[5],但子陣化也會造成附加的周期性，使柵瓣和旁瓣惡化。

圓環(huán)陣是另一種常用的稀疏陣列設計方案[6]。圓環(huán)陣在極坐標中以一定的規(guī)律排布，所以優(yōu)化調整參數(shù)較少，設計較為方便快捷，易于形成在直角坐標中無序的排列，達到柵瓣抑制效果，但是平均副瓣電平較高。環(huán)形稀疏陣的優(yōu)化參數(shù)有圓環(huán)半徑遞增量、單圈圓環(huán)上等角分布的單元數(shù)量、每圈單元起始位置角度等。對于小規(guī)模圓環(huán)陣，可使用遺傳算法優(yōu)化對上述參數(shù)進行搜索尋優(yōu)。由于在每一步優(yōu)化過程中要對多個指向的方向圖積分再計算代價函數(shù)，其計算量巨大，優(yōu)化效率仍相對較低。如要獲得更低的副瓣則半徑遞增量較大[7]，導致陣元密度不均勻，不適合K/Ka頻段寬帶通信相控陣天線的要求。

如能跳出全局優(yōu)化算法的框架，利用數(shù)學、物理、仿生學等理論，尋找稀疏陣列輻射特性與陣列布局的映射關系，將大幅提高稀疏陣列的設計效率。這種思想在電磁場及微波學科已有多種成功案例，比如螺旋天線的非頻變超寬帶效應[8]，分形幾何的自相似性賦予天線的超寬帶特性[9]。文獻[10]介紹了一種斐波那契網(wǎng)格稀疏陣列設計方案，用于實現(xiàn)大間距陣列的柵瓣抑制。這種布陣方案由解析公式給出，無需使用如遺傳算法這類大規(guī)模的數(shù)值計算，所以非常高效，在工程中可以大幅簡化陣因子設計流程，直接跨入三維電磁場仿真。該文獻在標準的斐波那契網(wǎng)格上疊加徑向擴展因子構成密度加權陣，對旁瓣電平進行控制。

本文從積分變換和數(shù)論等數(shù)學原理上對斐波那契網(wǎng)格稀疏陣列的柵瓣抑制特性進行分析和解釋。相比現(xiàn)有文獻，增加了斐波那契網(wǎng)格的均勻性和無序性的理論分析，解釋了斐波那契網(wǎng)格用于相控陣工程中天然具有柵瓣抑制特性的機理。另外，利用輕微的幅度加權進一步抑制旁瓣的分析，這和現(xiàn)有文獻采用的密度加權稀疏化抑制旁瓣的方式相比有創(chuàng)新，也更匹配寬帶K/Ka頻段通信相控陣天線的需求。本文設計出的斐波那契網(wǎng)格稀疏陣列具有大間距、網(wǎng)格均勻、低副瓣、無柵瓣、寬角高增益的特性，在K/Ka頻段有源相控陣工程中應用前景廣闊。

1 基于斐波那契網(wǎng)格的稀疏圓陣設計

以上列舉的衛(wèi)星通信K/Ka頻段相控陣天線稀疏化柵瓣抑制布局要求可總結為陣列網(wǎng)格無序、宏觀均勻，在數(shù)學中被稱為Tammes問題，即二維三維的裝箱問題(Packing Problem)。用數(shù)學語言描述為：將點在平面或曲面上均勻鋪開以達到各點的最小距離最大化[11]。六邊形網(wǎng)格是平面Tammes問題的最優(yōu)解，但網(wǎng)格有序，應用在大間距平面相控陣中時會出現(xiàn)柵瓣。

1.1 斐波那契網(wǎng)格定義

斐波那契網(wǎng)格是使用黃金分割比為角度增長系數(shù)的密繞螺旋，可以在球面或圓平面上生成無序且宏觀均勻分布的點云[11-13]。

斐波那契網(wǎng)格具有簡單的表達式[11]，以平面陣為例：

(1)

1.2 斐波那契網(wǎng)格均勻性解釋

圓可以用極坐標和直角坐標表示[13]，其變換式為

(2)

直角坐標和極坐標進行積分變換的雅可比行列式為

(3)

則積分元為

(4)

(5)

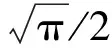
1.3 斐波那契網(wǎng)格無序性解釋

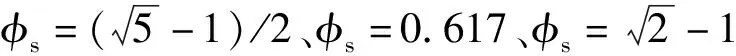
可以用數(shù)論的連分式展開理論[12，14]解釋以上圖形的周期性螺旋條紋。

任意一個實數(shù)a都可以展開為連分式：

(6)

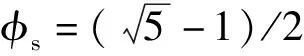
圖1 斐波那契網(wǎng)格詳圖

把a的連分式在某一項截斷，得到a的有理逼近，稱為丟番圖逼近(Diophantine Approximation)。如果截斷到ak，化簡后得到的最簡分數(shù)為pk/qk。pk和qk可以有以下遞推公式求得

pk=akpk-1+pk-2,

(7)

qk=akqk-1+qk-2。

(8)

式中：p0=a0，q0=1，p-1=1，q-1=0。定義逼近誤差k=|qka-pk|。

φs=0.617的連分式為[0;1,1,1,1,1,1,3,21]，各階丟番圖逼近項與誤差如表1所示。

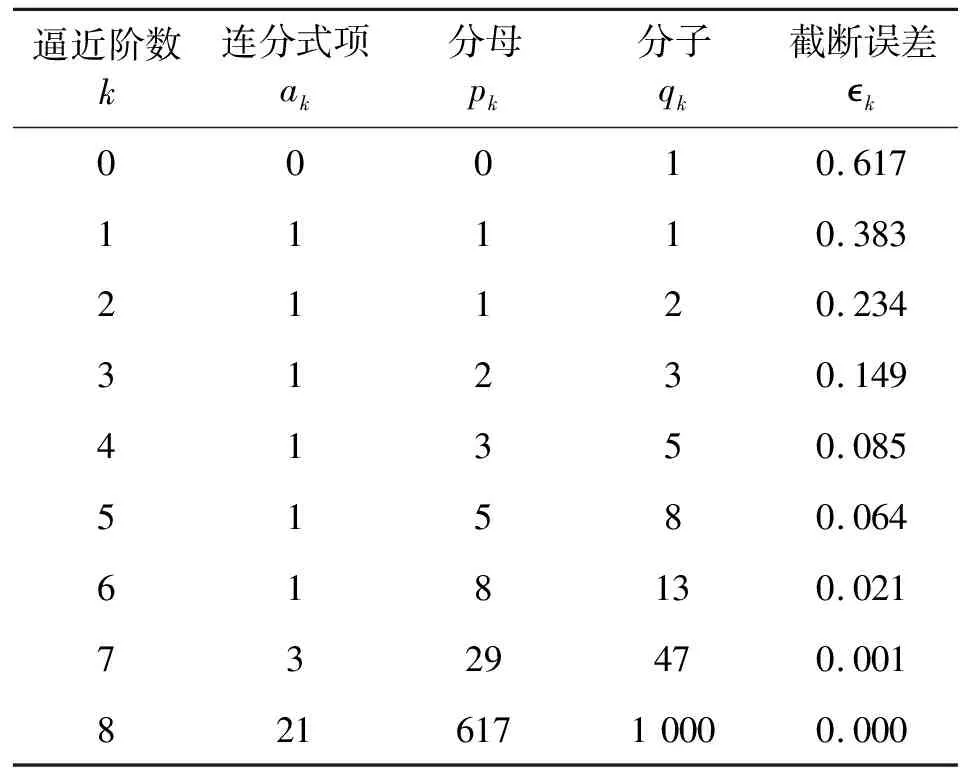
表1 0.617的各階丟番圖逼近項與誤差

圖2畫出了φs=0.617時1～400點圖形，可以看出，在原點附近點云形成較明顯的13條螺旋臂，而在外圍點云呈47條射線狀，13和47是丟番圖逼近的分母。將螺旋臂和射線的這種顯著的排列稱為模式，本圖中的模式編號為8/13模式和29/47模式。

圖2 φs=0.617的密繞螺旋詳圖

利用丟番圖逼近，將無理數(shù)連分式截斷，如產(chǎn)生截斷項ai的激增，點云圖中就會出現(xiàn)十分顯著的模式。

黃金分割比的連分式項全為1，非常穩(wěn)定，模式切換頻繁但沒有較大的突變，這種特性正是形成無序但宏觀均勻分布點云的原因：均勻是因為在任何半徑處各模式的差異非常小，不會出現(xiàn)大的間距；無序是因為每種模式都不會持續(xù)很久。

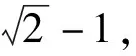
圖的密繞螺旋詳圖

1.4 576元陣列數(shù)值算例

基于以上分析，斐波那契網(wǎng)格完美解決了平面點的均勻且無序地排列問題。根據(jù)陣列天線的柵瓣產(chǎn)生的機理[2]，我們認為采用斐波那契網(wǎng)格能對大間距陣列的柵瓣進行有效抑制。以下進行數(shù)值仿真，分析斐波那契網(wǎng)格及另外幾種具有類似幾何特性的網(wǎng)格對陣列的柵瓣、副瓣等指標的影響，找到其關鍵設計參數(shù)。

首先對工作在20 GHz的576元陣進行數(shù)值仿真[15]，分析其陣因子方向圖。取不同的φs，并調整縮放比例使576元分布在半徑0.3 m的口徑中，等效間距DE≈1.48λ。陣列數(shù)值仿真結果如圖4～6所示，采用天線工程中的uv空間投影方向圖形式，便于觀察整個上半空間的副瓣，其中心為法向，徑向為俯仰角，周向為方位角，幅度采用歸一化增益值，單位為dB。由于陣列規(guī)模較大，可以看出能實現(xiàn)相當于圓口徑等副加權的-17 dB副瓣電平。

圖陣列uv空間歸一化方向圖

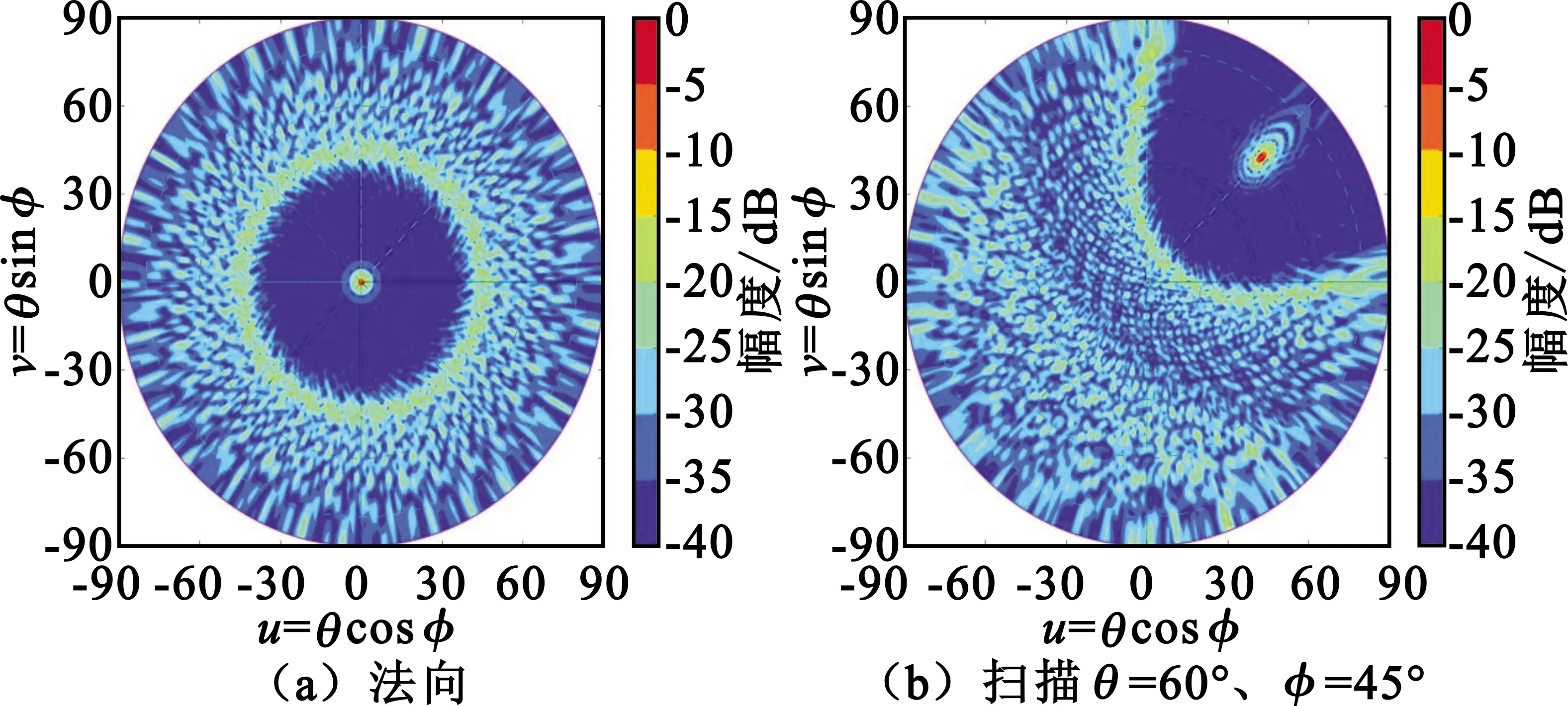
圖5 φs=0.617陣列uv空間歸一化方向圖

圖陣列uv空間歸一化方向圖

從前面三組方向圖可見，副瓣區(qū)域能量分配很均勻、無序。三個參數(shù)得到的副瓣電平相當，φs=0.617最好。但根據(jù)圖形特性，黃金分割點云分布最為均勻、緊湊，可以任意等比縮放，較適合于分析相控陣不同間距(即寬頻帶)的特性。

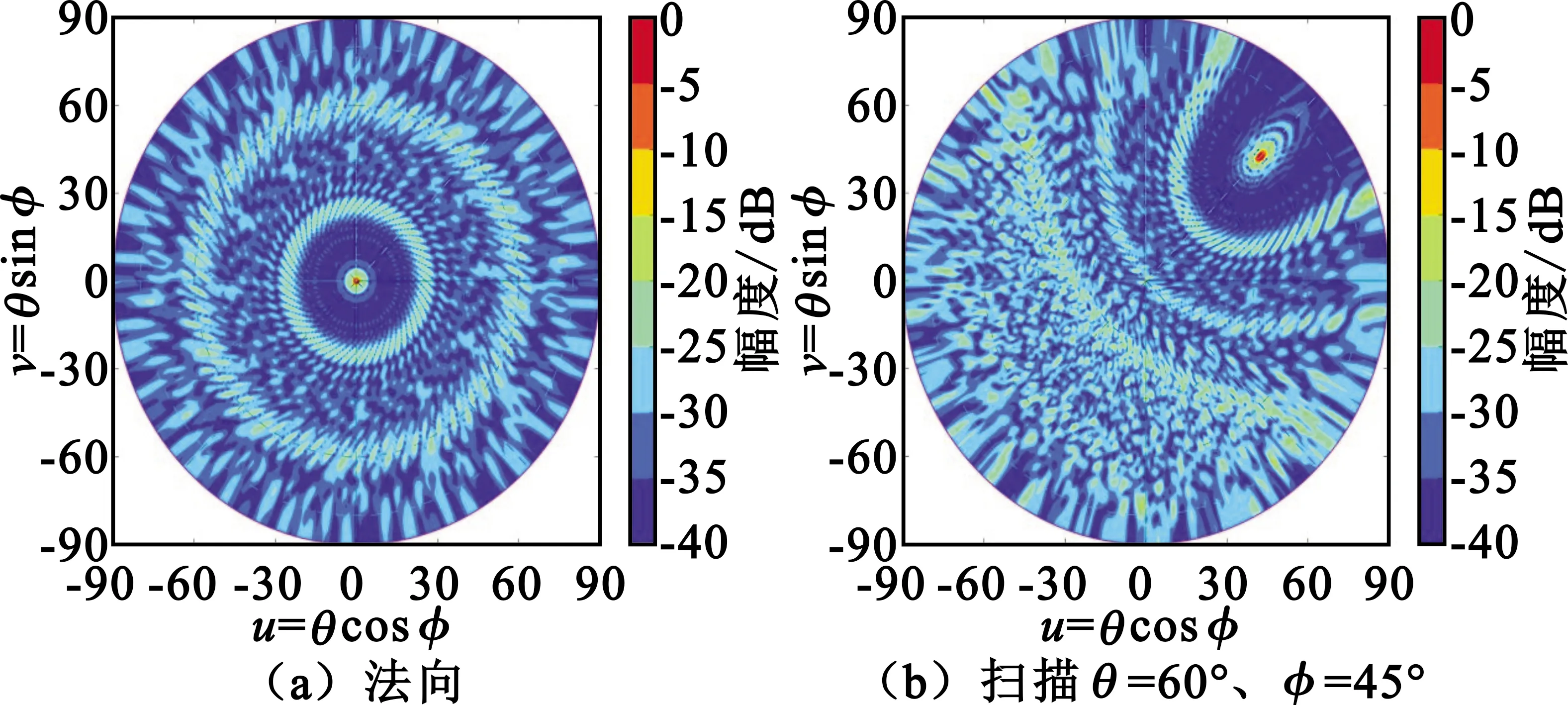
表2給出了576單元按不同縮放比例的形成陣列的副瓣電平計算結果。陣列半徑相差2倍以上，副瓣電平無明顯差異，均能達到-16 dB以上，可見這種陣列具有穩(wěn)定的寬帶副瓣特性。

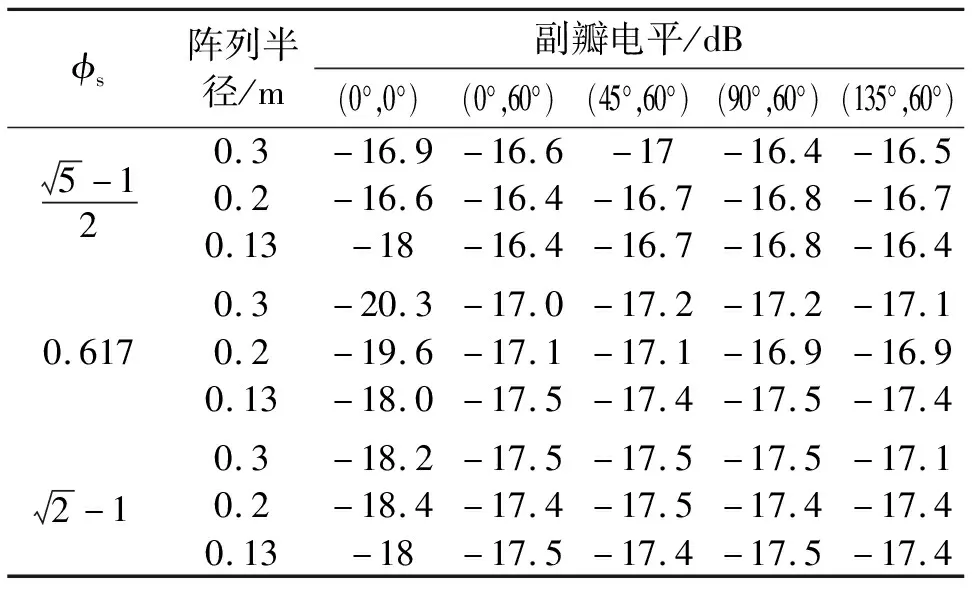
表2 不同φs和半徑的網(wǎng)格陣因子副瓣

下面詳細分析斐波那契網(wǎng)格陣列的副瓣特性。圖7列出了576元陣列在不同方位面的方向圖，可看出，最高副瓣為第一副瓣，其電平值約為-17.3 dB，接近等功率分布的圓口徑副瓣理論值。而遠副瓣分布較為平均，指向為法向時遠副瓣電平達到-25 dB，指向大角度(掃描θ=60°、φ=45°)時，遠副瓣抬高至約-20 dB。實際遠副瓣電平與陣元數(shù)量和單元方向圖有很大的關系，結合下文的156元陣列分析和電磁場仿真可得出結論，斐波那契網(wǎng)格稀疏陣列的副瓣電平隨單元數(shù)的增加而改善，天線單元因子及結構件也能顯著抑制副瓣。

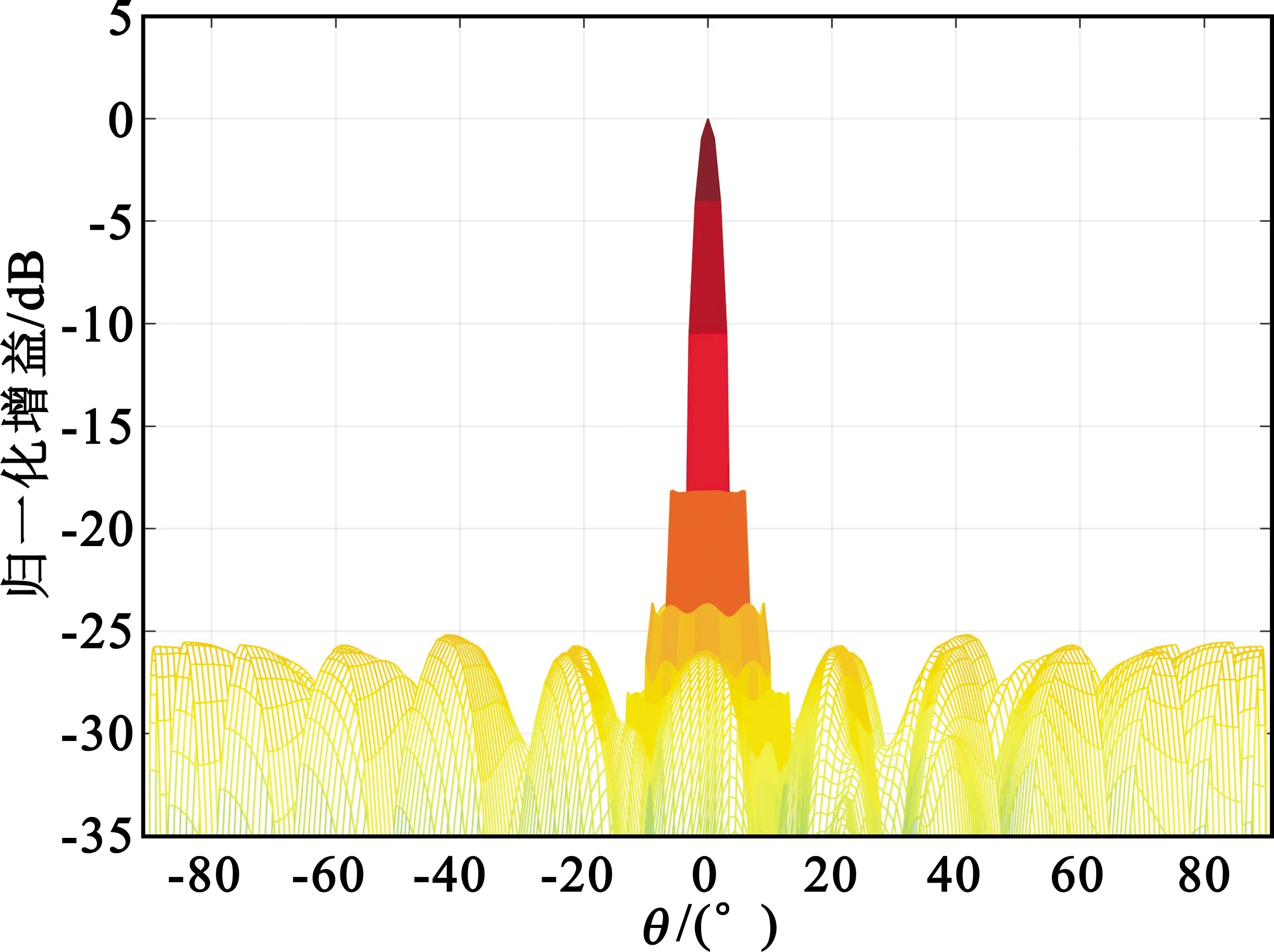
(a)法向

在K/Ka頻段通信中，考慮到功放芯片的效率較低并簡化控制芯片的設計，一般情況下-20 dB的副瓣電平已完全滿足系統(tǒng)需求，所以未對有源相控陣天線的副瓣做進一步的抑制。文獻[8]采用密度加權方式進行副瓣抑制，這樣造成陣元間距沿徑向逐漸擴展，陣列網(wǎng)格不均勻，TR組件芯片與陣元位置及各射頻通道的時延難以匹配。

近來低軌衛(wèi)星寬帶網(wǎng)絡提出了相控陣天線多波束復用的要求，各波束間需滿足頻域和空域的隔離度，所以副瓣電平在天線指標體系中的重要性逐步提升。為了克服密度加權方式在K/Ka頻段有源相控陣中的不足，本文采用幅度加權抑制副瓣技術。

圖8算例中，幅度加權采取從1～576元逐漸衰減地漸變加權，電壓幅度歸一化加權系數(shù)wn=n-0.15，中心和邊緣功率加權相差約8 dB，第一副瓣電平可以抑制到-23 dB。當電壓幅度歸一化加權系數(shù)wn=n-0.05，中心和邊緣功率加權相差約3 dB，第一副瓣電平可以抑制到-18.5 dB。

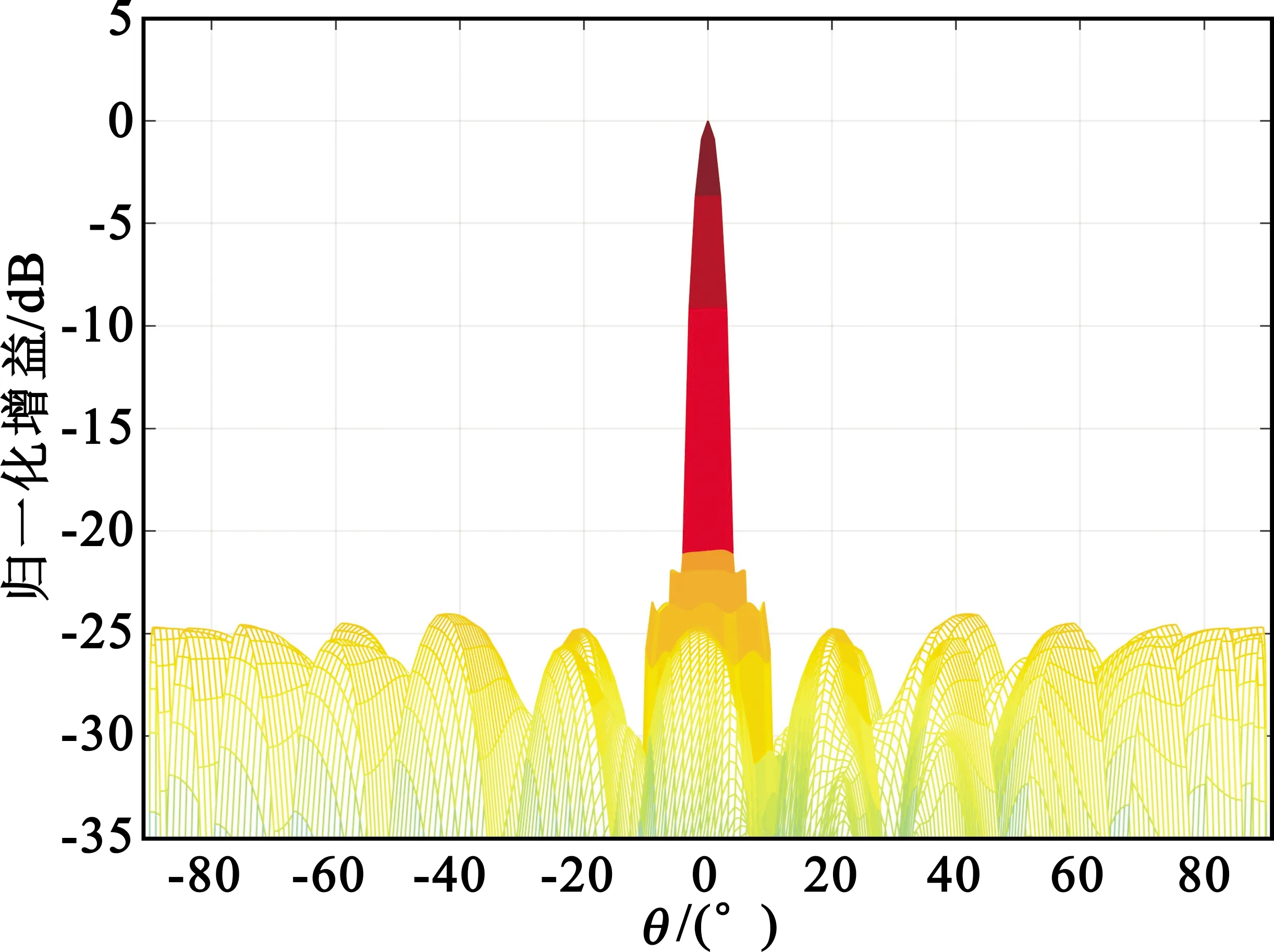
(a)法向

圖9算例中，幅度加權采取1～576元1、0.707兩檔位衰減的階梯量化加權，電壓幅度歸一化加權系數(shù)wn=1,n∈(1,288),wn=0.707,n∈(289,576)，副瓣電平可以抑制到-19.5 dB。

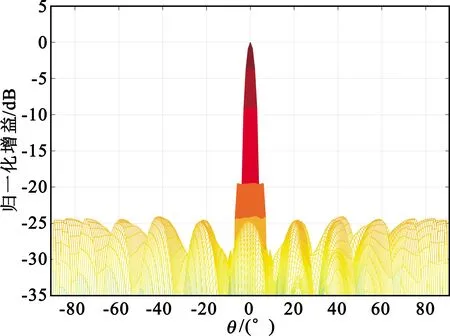
(a)法向

從以上幾個算例可看出，采用輕微的幅度加權，即可將第一副瓣電平抑制。工程中，K/Ka頻段相控陣控制芯片中配置有高精度數(shù)控移相器和衰減器，幅度加權易于實現(xiàn)。

采用幅度加權后，陣列口徑增益損失LGain由下式得到：

(9)

式中：N為陣元數(shù)。以上幾種輕微幅度加權，對天線的增益影響不超過0.2 dB，所以對接收天線品質因數(shù)(增益噪聲比，G/T值)不會產(chǎn)生明顯影響，只是對于發(fā)射天線來說要維持等效全向輻射功率(Equivalent Isotropic Radiation Power，EIRP)不變，總的有源功率輸出應為等功率加權的N/∑wn2倍。

1.5 156元陣列數(shù)值算例

對工作在20 GHz的156元陣進行計算，取不同的φs，并調整縮放比例使156元分布在半徑0.15 m的口徑中，實現(xiàn)約1.48λ的等效間距；或使其分布在半徑0.075 m的口徑中，實現(xiàn)約0.7λ的等效間距。

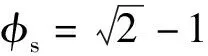
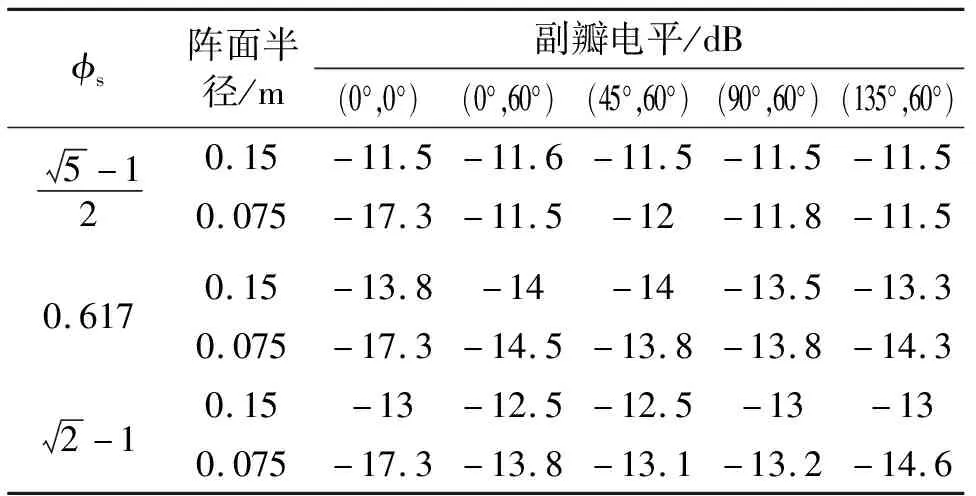
表3 156元陣陣因子副瓣

2 陣面三維電磁場仿真設計

2.1 陣面仿真

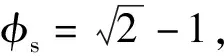
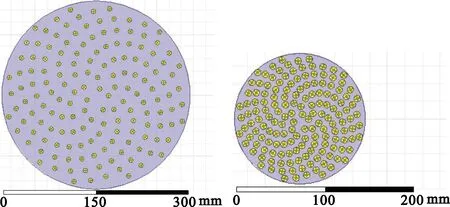
圖10 陣面的HFSS仿真模型圖

由于陣列的宏觀均勻性，各掃描角度均沒有顯著的副瓣，所以只列出0°方位切面的方向圖，見圖11、圖12、表4、圖13、圖14和圖15所示。

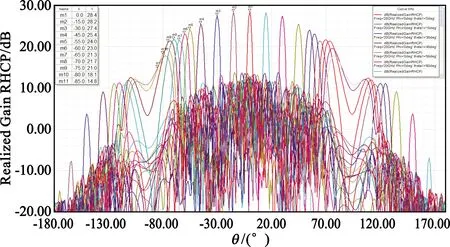
圖11 半徑0.15 m陣列HFSS仿真方向圖(0°方位切面掃描)

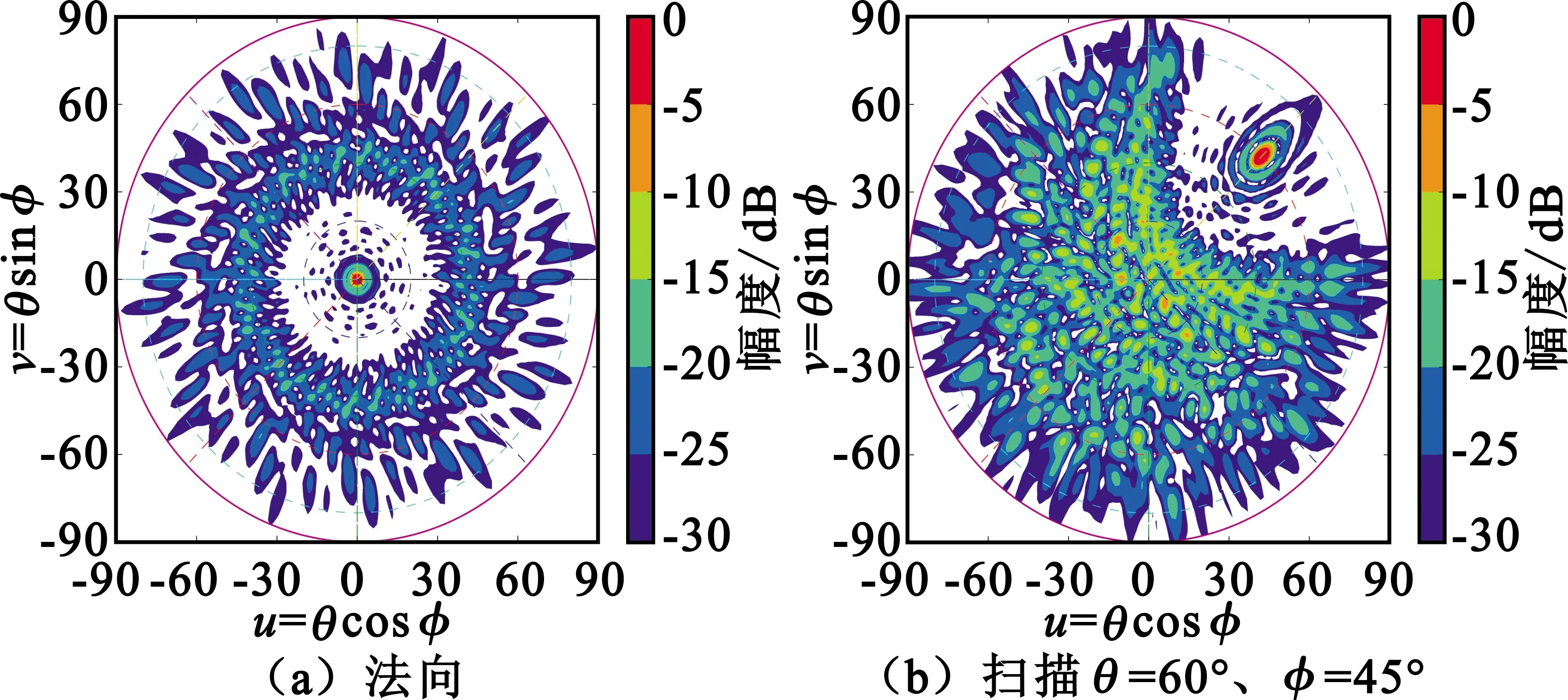
圖12 半徑0.15 m陣列HFSS仿真uv空間歸一化方向圖

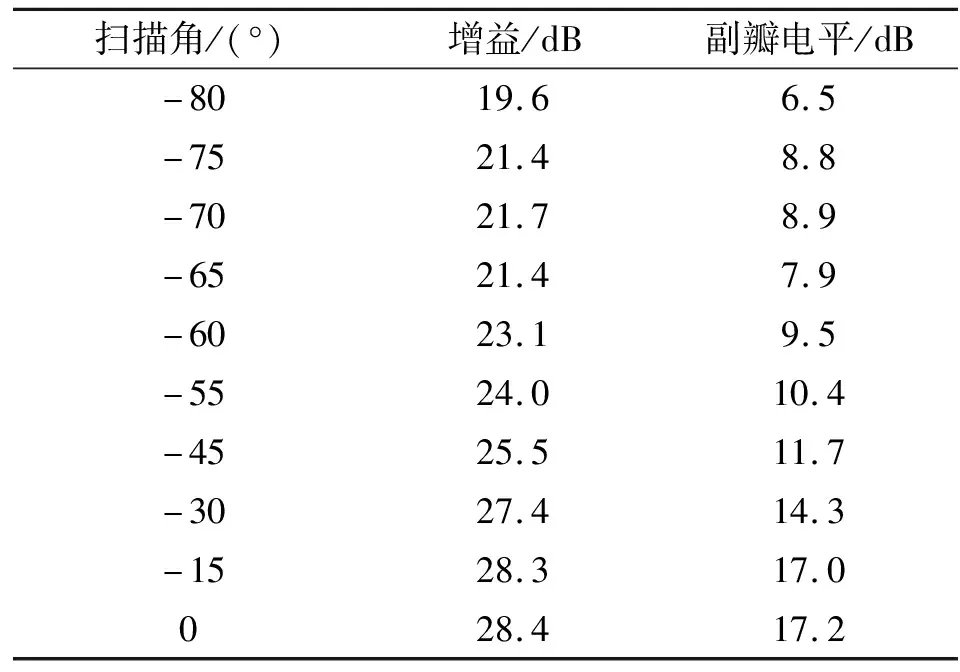
表4 半徑0.15 m陣列HFSS仿真結果

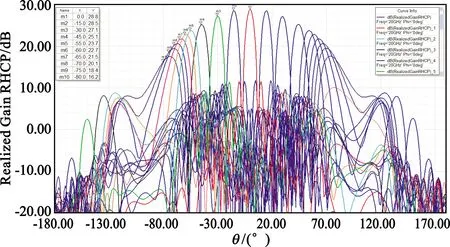
圖13 半徑0.075 m陣列HFSS仿真方向圖(0°方位切面掃描)

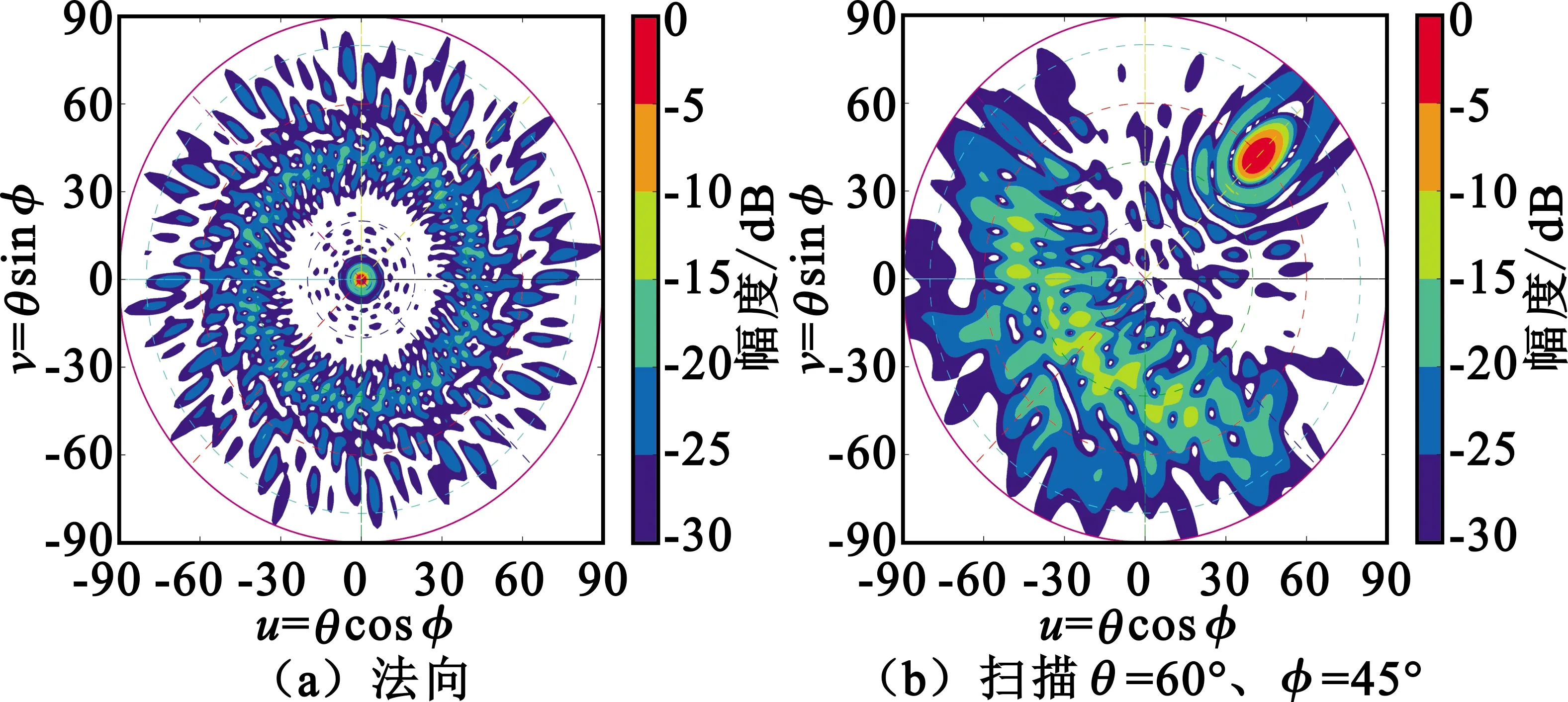
圖14 半徑0.075 m陣列HFSS仿真uv空間歸一化方向圖

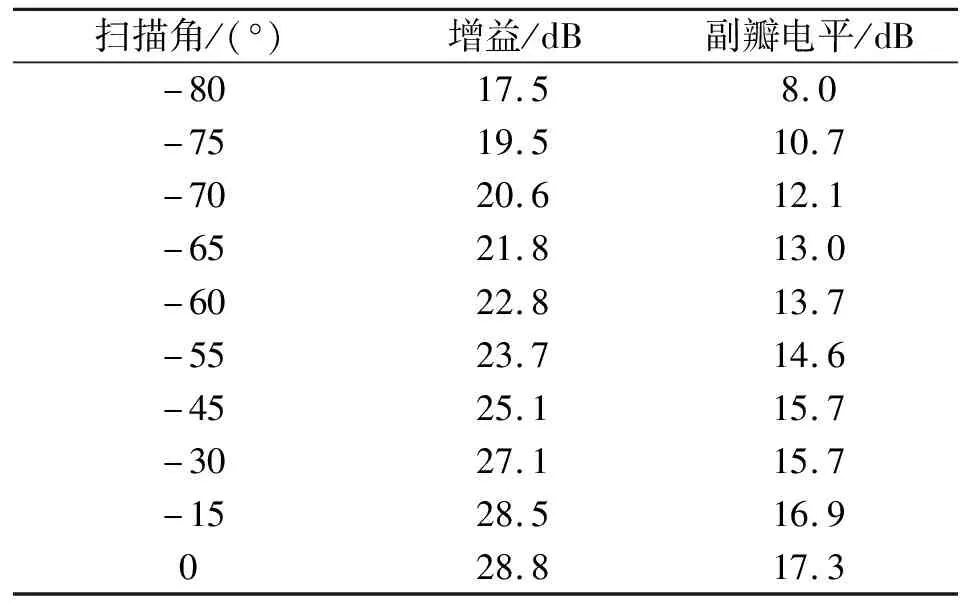
表5 半徑0.075 m陣列HFSS仿真結果

根據(jù)以上仿真結果可看出，在不同的陣列元間距條件下，掃描方向圖呈現(xiàn)不同的特性。半徑0.15 m陣列掃描至75°增益可達21.4 dB，而掃描角大于60°時副瓣電平抬高；半徑0.075 m陣列掃描至65°增益可達21.8 dB，掃描至75°時副瓣電平仍維持在10.7 dB的水平。進一步分析可知，掃描角超過40°的情況下，最大副瓣均出現(xiàn)在90°以外，屬于相控陣掃描特有的后瓣，實際中由于天線安裝在面積遠大于輻射口徑的金屬平臺中，這種副瓣能被有效抑制。可繼續(xù)深入優(yōu)化陣列半徑，尋求副瓣的最優(yōu)結果。

下面分析斐波那契網(wǎng)格大間距稀疏陣列的寬角掃描特性機理。相控陣天線口徑增益可表示為

(10)

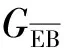
2.2 陣面與TR組件互連設計

針對工作在20 GHz半徑為0.15 m的156元陣，按照工程化的要求，對陣元和均勻排布的TR組件進行了接口匹配設計，如圖15所示。圖中正方形邊長為0.5λ，代表一般的諧振式陣列單元占據(jù)的面積；將所有單元分成4個象限，用四種顏色區(qū)分，是工程中為了避免電路面積過大造成加工成本高、焊接變形等問題的手段；2×2一組的紅點表示TR芯片輸出至天線單元的接口，間距為20 mm，則集成化的2×2通道TR芯片可利用面積為40 mm×40 mm，給工程化實現(xiàn)提供了相當大的自由度。陣元與鄰近的TR通道一一配對形成鏈表，就可以使用布板軟件進行轉接層圖紙自動化設計。

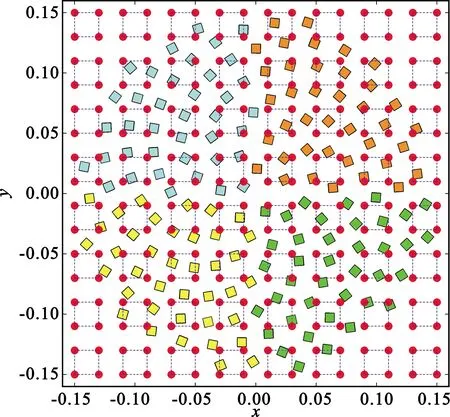
圖15 稀疏陣列單元與TR組件接口示意圖

3 結束語