車門限位器主臂曲線方程及力學性能變化規律研究

潘毓濱 代世磊 張敏

（1.廣汽蔚來新能源汽車科技有限公司，廣州 511434；2.申雅密封件（廣州）有限公司，廣州 511434）

主題詞：車門限位器 限位臂曲線 解析方程 迭代法 設計優化 力學性能

1 前言

隨著汽車的大量普及，消費者越來越注重用戶體驗。車門開閉感（用戶開關車門的體驗感）作為潛在用戶考察車輛時最先產生的操作體驗，逐漸成為汽車生產廠商的重點研究內容[1-5]。車門開閉感的影響因素眾多，主要包括車門總成、限位器、鉸鏈、密封條、門鎖和外開手柄等。限位器不僅為車門提供保持功能，而且影響著車門的關門能量和開、關車門時的操作手感，在提升車門開閉感時需要重點研究[6-14]。限位器主臂曲線對車門開閉感和空間布置都存在很大影響，其設計過程貫穿車型前期概念設計至后期詳細設計多個階段，是限位器設計的重點內容[15-16]。目前，一般采用迭代作圖法[17-18]，或者基于迭代作圖法原理編程的方法[19]設計限位器主臂曲線。但是傳統的迭代作圖法精度較差，而編程的方法門檻較高，不便于廣泛采用，因此，亟需尋找一種便于使用且具有較高精度的方法。限位臂曲線的設計往往不是一蹴而就的，一般需要經過反復優化，才能得到形狀、尺寸和力學性能均理想的結果。目前，行業內還沒有關于限位臂曲線及力學性能變化規律的系統性研究成果[20-21]，限位臂的優化過程效率較低。在研究限位臂曲線及力學性能變化規律時，如何選定分析參數非常重要，分析角度、坐標系和布置方案不同，可以定義不同的分析參數。本文在大量設計布置經驗基礎上，結合理論分析分別研究不同設計參數對限位臂曲線和力學性能的影響規律。

2 限位器主臂曲線解析方程求解

2.1 限位臂-車門運動分析模型建立

如圖1 所示，限位臂與限位盒中的滑塊在A0處嚙合，A為曲線中的某一點。車門開啟角度為θ時，限位臂曲線上A點運動到A′處，同時，限位盒（固定在車門上）上A0也運動到A′處，此時，限位臂與限位盒中的滑塊在A′處嚙合。

圖1 限位器示意

如圖2所示，過A′點且垂直于鉸鏈軸線的平面與鉸鏈軸線、限位器軸線分別相交于O、O′，記該平面為OO′A′。設θ為OA′與OA0的夾角，代表車門開啟角度，在初始狀態位置，θ=0°；設ξ為OA0與OO′的夾角；設φA、φA′分別為O′A、O′A′與OO′的夾角。車門開啟角度為θ時，限位臂對應轉過的角度為φ=φA′-φA。需要說明的是，在任意狀態下，限位臂中心線上每個點對應的φA和φA′均不一定相同，但轉過的角度φ卻是相等的。

圖2 限位器運動分析示意

記車門開啟角度為θ時，限位臂中心線在A′點處的切線單位向量為n，法向單位向量為m，n和m的方向均指向車身外側。n與A′O、A′O′以及O′O的夾角分別為α、β、δ，車門開啟過程中α始終為定值，一般地，0＜α＜π/2，且有δ=θ+ξ+α。記限位器盒在A′點處的運動速度為v1，車門開啟角速度為ω1，限位臂在A′點處的運動速度為v2，限位臂運動角速度為ω2。

2.2 限位器主臂曲線解析方程推導

在平面OO′A′上，以OO′為縱軸，建立平面坐標系x′Oy′，本文以x′Oy′為基準坐標系進行推導。

記O=(0,0)、O′=(0,l)、A=(x,y)、A′=(x′,y′)，令r1=OA=(x1,y1)，r2=O′A=(x2,y2)，r1、r2的模長分別為r1、r2，則有：

由于限位塊與限位臂在平面OO′A′上沿垂直于限位臂中心線方向上是相對靜止的，即v1與v2在m方向分量相等，故有：

由于m、v1與v2都是平面向量，根據向量的運算關系，可得：

所以有：

式中，a=l/(r1cosα)，且1-acos(θ+ξ+α)＞0。

可以看出，φ是關于θ的函數，通過積分運算化簡可得：

3 迭代法的驗證及優化

3.1 迭代法驗證

工程上，普遍采用迭代作圖法在軟件上設計限位臂曲線。將車門最大開啟角度均分成若干等份步長Δθ，逐步求解每步對應的限位臂曲線上的位置，從而近似擬合出整條曲線。迭代作圖法可分為前迭代法和后迭代法，如圖3 和圖4 所示，為限位臂曲線運動到處的切線。Si為直線與以O′為圓心且過點的圓的交點，車門從運動到過程中，前、后迭代法中限位臂分別對應轉過O′Si、∠Si-1O′。前迭代法和后迭代法原理相同，通過設計算法編寫程序[19]，便可求解出對應曲線。

圖3 前迭代法

圖4 后迭代法

分別采用限位臂曲線方程和迭代法求解限位臂曲線，參數設置如表1所示。前、后迭代法分別采用1°、5°和10°3個步長進行計算，求解結果如圖5所示。由圖5可知：前迭代法與后迭代法求解出的曲線均分列在理論曲線（通過曲線方程求得）兩側；在步長較大時，前、后迭代法求得的曲線差別較大；步長越小，2 種迭代法求得的曲線越接近理論曲線；當步長為1°時，2 條曲線較為接近，但仍然存在肉眼可見的差異。

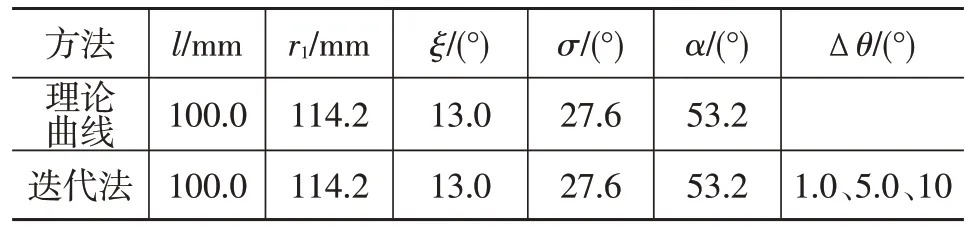
表1 采用解析方程和迭代法求解限位臂曲線的相關參數

對前、后迭代法的研究表明，前、后迭代法只有在步長小于1°時，才能求得比較接近理論曲線的結果，用手工繪圖的方式實現如此小的步長幾乎是不可能的。采用同樣步長，分別用前、后迭代法求得A11、A21、A31、……、AN1和A12、A22、A32、……、AN2，如圖6所示。分別取A11和A12的中點A1、A21和A22的中點A2、……、AN1和AN2的中點AN，將A0、A1、A2、……、AN連接成曲線，得到平均迭代法曲線。

圖5 前、后迭代法與理論曲線結果對比

3.2 平均迭代法

采用平均迭代法分別按步長為1°、5°和10°，求得相應曲線如圖7所示。從圖7中可以看到，以10°步長求得的平均迭代法曲線比以1°步長求得的前、后迭代法曲線都更加接近理論曲線，以1°步長求得的平均迭代法曲線與理論曲線幾乎完全貼合。顯然，采用平均迭代法，采用較大的步長、較少的步數，即可獲得精度較高的限位臂近似曲線。

4 布置參數對限位臂曲線的影響規律分析

在車門及附件系統的前期布置過程中，需要保證限位器運動包絡與車門密封條、車門玻璃、玻璃導軌、車門內板等零件之間有足夠的運動間隙，如圖8所示。

圖6 平均迭代法曲線構造方法

圖7 前、后迭代法和平均迭代法求解結果與理論曲線對比

4.1 布置參數定義

在設計限位臂曲線時，為了獲得最優方案，一般需要分析多種設計方案。如圖9所示，O′和A0分別為限位器旋轉中心和初始嚙合點位置，n0和m0為限位臂中心線在A0點的切線單位向量和法向單位向量。O″和分別為優化方案中的限位器旋轉中心和初始嚙合點位置，和為優化方案限位臂中心線在點的切線單位向量和法向單位向量。分別以平行于和并指向整車坐標系X和Y軸正方向為H軸和V軸，建立參考坐標系VA0H。在新坐標系下，O″相對O′的坐標變化為（ΔHO′,ΔVO′），相對A0坐標的變化為(ΔHA0,ΔVA0)，相對m0的夾角為η（以逆時針角度為正）。顯然，任意調整ΔHO′、ΔVO′、ΔHA0、ΔVA0和η、l、r1、ξ、α和σ都會對應發生變化。本文將分別研究改變ΔHO′、ΔVO′、ΔHA0、ΔVA0和η取值對限位臂曲線的影響規律。

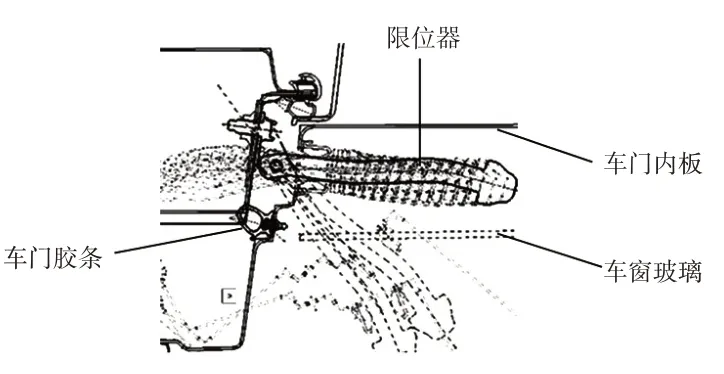
圖8 車門限位器包絡及周邊零件

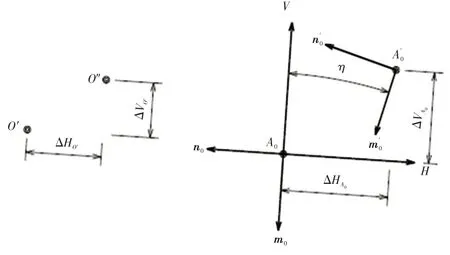
圖9 限位器布置參數定義

4.2 η對限位臂曲線的影響規律分析

設η為相對于m0轉過的角度，由于m0和一般平行于限位器安裝面，故η與沖壓工藝性和布置空間關系較大。取η分別為0°、-3°和-6°，設置曲線參數，求得對應的曲線如圖10 所示。由圖10 可知，相對m0繞順時針方向轉過的角度越大，限位臂曲線偏向車身外側方向越明顯，而曲線長度變化不明顯。

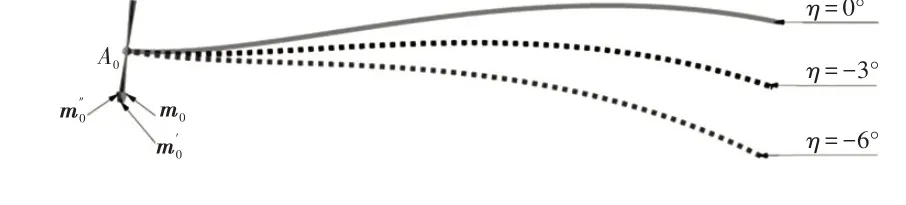
圖10 不同η對應的中心曲線

4.3 ΔHO′和ΔHA0對限位臂曲線的影響規律分析

分別設置ΔHO′和ΔHA0為±5 mm，求得對應曲線如圖11所示。從圖11中可知：當O″和沿H軸方向靠近對方，即ΔHO′＞0 或ΔHA0＜0 時，限位臂曲線偏向車身內側；當O″和沿H軸方向遠離對方，即ΔHO′＜0 或ΔHA0＞0 時，限位臂曲線偏向車身外側。ΔHO′的變化對曲線形狀位置的影響較ΔHA0顯著。

4.4 ΔVO′和ΔVA0對限位臂曲線的影響規律分析

分別設置ΔVO′和ΔVA0為±5 mm，求得對應曲線如圖12所示。從圖12中可知，ΔVO′和ΔVA0對限位臂曲線影響規律完全不同：ΔVA0對限位臂曲線位置影響較大，對曲線形狀和長度影響不明顯，改變ΔVA0，限位臂曲線的嚙合段幾乎都隨平行移動；ΔVO′對限位臂曲線的長度影響較為明顯，對限位臂曲線位置的影響不明顯，ΔVO′越大，限位臂曲線越長。

任何限位器布置優化方案均能通過ΔHO′、ΔVO′、ΔHA0、ΔVA0和η進行表征，因此，在限位器布置方案優化過程中，可以結合上述規律，快速判斷出限位臂曲線發生的變化，提高設計效率。

圖11 O′和A0在H方向不同相對位置對應的中心曲線

圖12 O′和A0在V方向不同相對位置對應的中心曲線

5 布置參數對限位器力學性能的影響規律分析

5.1 限位器力學分析

對限位臂進行受力分析，如圖13 和圖14 所示。限位臂受到限位盒沿中心曲線切向作用力Fx、法向作用力Fy以及平衡旋轉軸摩擦力矩Tf的作用，其中Fx和Fy可以分別分解為限位臂正面和側面受到沿中心曲線切向作用力Fx1、Fx2和法向作用力Fy1、Fy2。

限位器運動過程中，滑塊始終沿著限位臂曲線切向滑動（α為常數），在法向近乎相對靜止，所以|Fy1|≈0，故：

圖13 限位器主臂受力情況

圖14 限位器主臂對車門作用力分析示意

Fx1為限位器正面對滑塊沿中心曲線方向的切向作用力，可以根據限位臂正面幾何參數、滑塊結構參數、摩擦因數以及滑塊壓荷等參數計算得到。

令μc為限位臂側壁與滑塊間的摩擦因數，則有：

Fx和Fy的合力Fh沿著O′A′方向，一般地，Fh與Fx夾角較小，與Fy夾角較大，|Fy|明顯小于|Fx|，所以|Fx2|＜＜|Fx|，故：

定義限位器布置參數如表2所示，通過Adams建立限位器仿真分析模型，如圖15 所示。分析得到Fx1、Fx2及Fy1、Fy2隨車門開啟角度θ的變化曲線，如圖16 所示。從分析結果可知，|Fy1|＜＜|Fy2|，|Fx2|＜＜|Fx1|，說明上述力學分析和假設成立。

表2 限位器仿真分析模型參數定義

Fh可分解為沿r1方向的分力Fr和垂直與r1方向的分力Ft，由于Fh平行于r2，所以：

圖15 限位器仿真分析模型

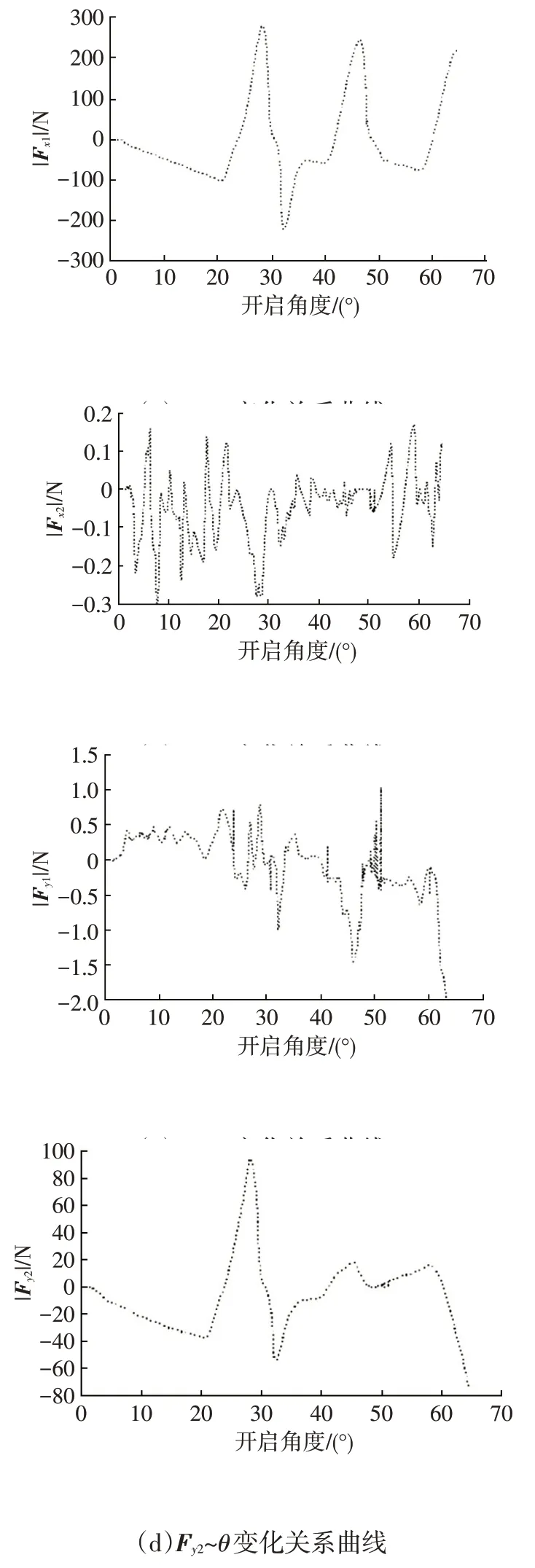
圖16 限位器主臂受力仿真分析結果

根據三角形幾何關系可求得：

令

限位器作用于車門的力矩T為：

聯立式（12）～式（15）可得：

從式（16）可以看出，d(θ)代表限位力的真實力臂，它是受ξ和α影響的、與θ相關的函數。通過式（16）和前述Adams仿真分析模型可以分別得到d(θ)隨θ的變化關系曲線，如圖17所示。從圖17中可知，由于是按動力學過程仿真，運動過程存在非平衡擾動，仿真結果圍繞理論值存在一定波動，但總體變化規律一致。

圖17 d(θ)隨θ變化的理論和仿真分析曲線

5.2 d(θ)的幾何含義

過O做n的垂線與O′A′或其延長線相交于B′，OB′與n交于BC′，則∠C′B′A′+β=π/2，可得：

顯然，|OB′|=d(θ)，所以OB′即為限位力的真實力臂。工程上，可以通過作圖法測出不同開啟角度下OB′的長度，從而快速求得不同車門開度下的限位力矩。

5.3 布置參數對d(θ)的影響規律研究

從式（16）可知，d(θ)的變化影響著限位力矩的變化。由式（14），分析l和r1對d(θ)的影響如下：

a.令r1=114 mm、ξ=13°、α=53.2°，取l分別為130 mm、114 mm、100 mm 和85 mm，得到d(θ)隨θ的變化曲線，如圖18所示。從圖18中可知，d(θ)隨l單調變化，l越大，d(θ)越大。

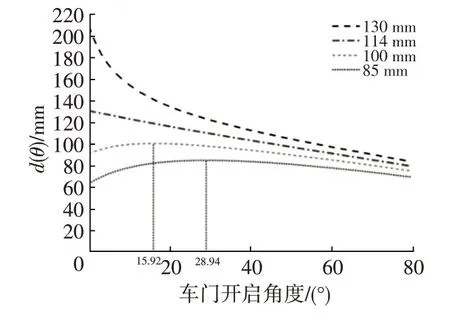
圖18 不同l取值下d(θ)隨θ的變化曲線

b.令l=100 mm、ξ=13°、α=53.2°，取r1分別為90 mm、100 mm、114 mm 和120 mm，得到d(θ)隨θ的變化曲線，如圖19 所示。從圖19 中可知，r1對d(θ)的影響與(θ+ξ+α)有關：0＜θ+ξ+α＜π/2 時，r1越大，d(θ)越小；π/2＜θ+ξ+α＜3π/2 時，r1越大，d(θ)越大；θ+ξ+α=π/2時，d(θ)不受r1影響。

圖19 不同r1取值下d(θ)隨θ的變化曲線

從上述分析可以發現，l和r1不僅影響d(θ)大小，也影響著d(θ)隨θ的變化規律。對d(θ)求導可得：

由于0＜α＜π/2，從式（18）可知，d(θ)隨θ的變化規律為：當l/r1≥1 時，d′(θ)≤0 恒成立，d(θ)隨著開啟角度θ增大而減小；當l/r1＜1 時，d(θ)隨著開啟角度先增大后減小。在θ=arccos(l/r1)-ξ時，d′(θ)=0，此時d(θ)最大，d(θ)max=l/sin[arccos(l/r1)+α]。d(θ)max也與α有關，當α=arcsin(l/r1)時，d(θ)max最小，等于l/r1，如圖20 所示。從圖20中可知，α不影響d(θ)的總體變化趨勢，但影響其變化幅度，α越大，d(θ)變化幅度越小。

圖20 不同α取值下d(θ)隨θ的變化曲線

5.4 布置參數對β(θ)的影響規律研究

對限位臂進行受力分析可知：

一般地，為了保護限位臂及滑塊，以及能夠更加準確地設計限位力，優化限位器布置方案時通常盡量減小Fy和Fx2，因此，需要盡量減小β。

因為γ=α+β，由式（19）可得：

所以β也是關于θ的函數，記為β(θ)，從式（20）可知，l和r1對β(θ)的影響都是單調的，l越大，β(θ)越大（見圖21）；r1越大，β(θ)越小（見圖22）。

圖21 不同l取值下β(θ)隨θ的變化曲線

圖22 不同r1取值下β(θ)隨θ的變化曲線

可以證明，β(θ)與d(θ)具有相同單調性：當l/r1≥1時，β(θ)隨θ增大而減小；當l/r1＜1 時，β(θ)隨θ先增大后減小。當θ=arccos(l/r1)-ξ時，β(θ) 最 大，此 時β(θ)max受α的影響如圖23 所示：當α＜arcsin(l/r1)時，β(θ)max＞0；當α=arcsin(l/r1)時，β(θ)max=0；當α＞arcsin(l/r1)時，β(θ)max＜0。從圖23中可知，α越小，β(θ)越大，改變α，能整體改變β(θ)。

圖23 不同α取值下β(θ)隨θ的變化曲線

從上述分析可知：l和r1均對β(θ)存在影響，l越大，r1越小，β(θ)將越大；通過調節l/r1，可以改變β(θ)隨θ的變化規律，以及β(θ)的變化幅度。一般建議l/r1＜1，且適當減小l/r1，增大β(θ)最大值對應的角度，以減小β(θ)的變化幅度。通過合理調節α，將α設計成適當小于arcsin(l/r1)的角度，可以使得β(θ)始終在0°附近的較小角度內變化。工程上，一般建議將|β(θ)|設置在15°以內。

6 結論

a.當車門及限位器布置參數l、r1、ξ、α和σ確定后，根據限位器主臂曲線方程即可求解出限位器主臂曲線；

b.相較于前、后迭代法，更建議采用平均迭代法進行手工繪制高精度限位器主臂中心曲線；

c.ΔHO′、ΔVO′、ΔHA0、ΔVA0和η對限位臂曲線有著不同的影響規律，在優化限位器曲線時，可結合相應規律，提高設計效率；

d.設計限位器時，目標是使得d(θ)盡量大，而|β(θ)|盡量小，l、r1、α對d(θ)和β(θ)的影響規律較為復雜，設計中應結合其影響規律進行反復優化。一般建議適當減小l/r1，使得l/r1＜1，同時，應使α＜arcsin(l/r1)。