基于連通域的復雜背景下粘連單元分割算法

姚夢潔

（山東科技大學測繪與空間信息學院，山東青島 266590）

0 引言

20 世紀70 年代計算機性能提升，可處理圖像等大規模數據，研究者可利用計算機代替人類視覺器官認識世界，計算機視覺逐漸受到關注。通過計算機實現自動讀取、識別客觀世界，代替人腦進行處理，實現人工智能是該學科探索方向［1］。近年來計算機視覺技術飛速發展，在醫學、工業等方面應用廣泛，如何實現生活生產過程自動化成為研究焦點［2］。計算機具有機械性特點，一方面可快速批量進行大數據處理，另一方面根據機械命令運轉。因此需將人腦機能通過冗長、復雜的程序轉化為計算機機械性語言［3］。

在工業生產中，產品質檢必不可少，利用計算機實現生產過程自動化是目前工業生產研究熱點［4］。在工業質檢中，需要檢查產品組成成分數量是否達標，但這些組成成分往往粘連嚴重且背景復雜，因此粘連單元數量檢測成為工業生產中計算機視覺應用難點［5-6］。現有處理粘連單元的主要方法是通過分割算法將粘連單元分離開來。葉明等［7］對粘連顆粒圖像中心點進行識別，利用先驗圖像前景輪廓對圖像進行檢測確定中心點；蘆念加等［8］先進行粘連物體中心核提取，根據中心核進行極限腐蝕并分割圖像；何磊等［9］利用自適應極大值方法對分水嶺過分割問題進行改進；李永鋒等［10］通過距離變換改進分水嶺算法，對粘連大米進行分割；高揚等［11］基于模糊距離變換改進了顆粒分割算法；魏瑾等［12］將模糊距離與分水嶺算法相結合。上述方法研究對象只有小部分粘連，粘連單元粘連程度較低，且粘連單元之間有空隙，部分算法只適用于特定形狀，因此在實際生產中實用性不強，并不適用于粘連嚴重背景復雜的分割，所以研究粘連單元分割算法具有重要意義。

一般通過檢驗纖維產品組成單元數量判斷其是否符合生產標準。目前通過計算機進行自動數量檢測主要借助連通域計數。該方法先對待檢測的圖像進行二值化，然后利用種子算法形成多個連通域，通過檢測連通域數量得到纖維粘連單元數量。但是在實際生產中，高清纖維單元照片往往背景復雜且存在粘連現象，復雜的背景難以去除且多個單元粘連容易被錯認為是1 個連通域，所以數量檢測難度較大。針對纖維粘連單元數量檢測難點，本文采用波段運算解決背景復雜問題，采用邊緣檢測與連通域標記的方法解決纖維單元粘連問題。

1 數據預處理

工業生產圖像背景復雜，后續操作容易造成很大誤差，因此需將前景從復雜背景中提取出來，進行前景、背景分離，所檢測的前景往往與背景在顏色或亮度等方面存在較大差異。針對粘連單元和背景差異，本文利用波段運算方法去除背景，通過觀察各波段圖像之間的關系進行波段間加減運算，最終去除背景。

本文實驗圖像是從工廠直接拍攝得到的樣本圖，由于相機相位及各項校正參數等可控，所以在進行粘連物體數量檢測時可忽略位置、相機拍攝等客觀條件的影響。

原始實驗圖像如圖1（彩圖掃描OSID 碼可見）所示。圖1（a）、圖1（b）分別為同一相機位拍攝的不同纖維圖像。中間顆粒狀物體為纖維單元，周圍藍色和白色部分均為雜亂背景。連通域進行數量檢測是根據像元亮度值進行判斷，將像元在一定亮度范圍之內的纖維單元二值化后進行數量檢測。圖1 中纖維單元和復雜背景像元范圍沒有明確界限，甚至是相互交叉的關系，因而利用連通域進行數量檢測時需先將纖維單元與雜亂的背景分離。

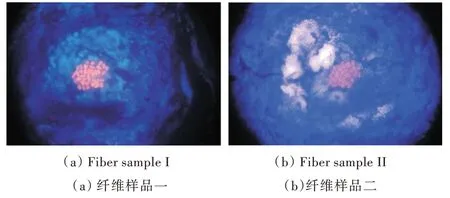
Fig.1 Fiber adhesion unit samples圖1 纖維粘連單元樣品

為了找到纖維單元與背景的分離方法，本文利用ENVI軟件統計R、G、B 3 個波段圖像元亮度值，其分布如圖2 所示。圖3 是紅光波段圖像，亮度值高的區域是需檢測的纖維單元；圖4 是綠光波段圖像，亮度值較高的區域是纖維單元及其周圍背景；圖5 為藍光波段，圖中亮度值相對較高的地方主要是背景部分。本文利用波段運算的方法去除背景，從圖2 可以看出，利用紅光波段或綠光波段與藍光波段作差可得到纖維單元，但對3 個波段亮度值分布進行分析可知，紅光波段亮度值較高的像元非常多，作差以后容易產生纖維單元，導致整個區域高亮、看不出邊緣，而采用綠光波段與藍光波段做差則能取得較好的檢測結果。

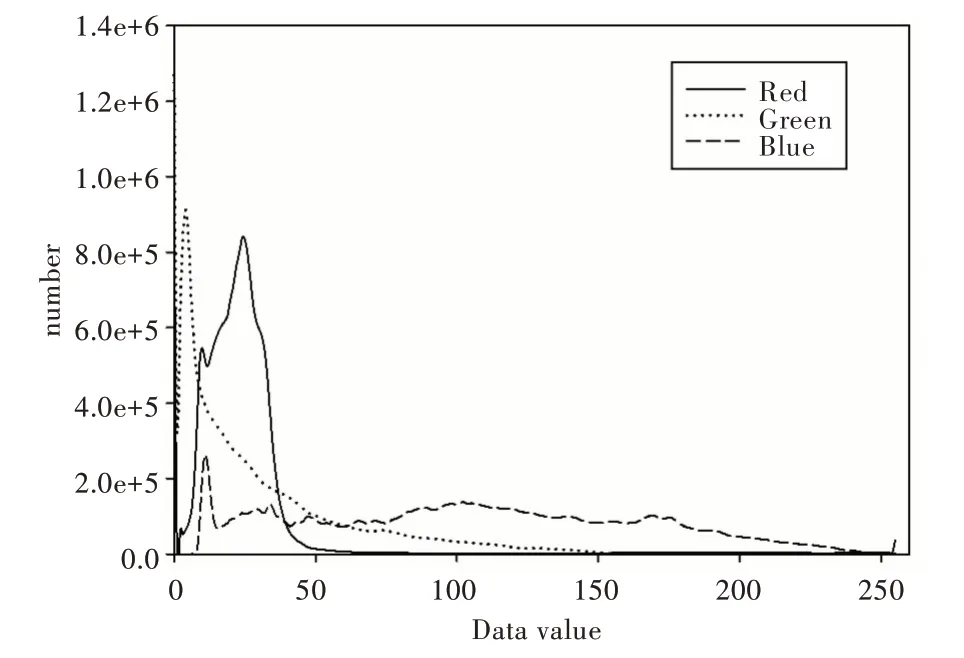
Fig.2 Distribution of brightness valus圖2 像元亮度值分布

Fig.3 R-band image圖3 R 波段圖像

Fig.4 G-band image圖4 G 波段圖像

Fig.5 B-band image圖5 B 波段圖像

在進行波段運算時，在部分背景區域出現像元值相減之后小于0，本文將這些小于零的值均賦為零。但由于波段運算得到的纖維單元圖存在亮度較暗的雜質，所以將去除背景后的圖像進行高斯濾波，以提高纖維單元提取純度。本文運用該波段運算方法對40 多個纖維樣本圖進行背景提取，其中4 個樣本圖背景去除后的結果如圖6 所示。

2 原理與方法

經過數據預處理得到的纖維單元仍存在粘連，本文通過邊緣檢測得到纖維粘連單元邊界，然后將去除背景纖維單元圖與邊緣檢測圖做差得到獨立纖維單元，從而利用連通域與種子算法進行檢測即可得到纖維單元數量。

Fig.6 Results after background removal圖6 背景去除后的結果

2.1 邊緣檢測

計算機視覺應用中最常用的兩種邊緣檢測技術是閾值法與邊緣連接法。在閾值法中，利用鄰域算子對圖像灰度進行不連續性增強［13］。邊緣檢測是一種基于物體與背景間灰度或紋理特性中某種不連續性或突變性的檢測技術。目前在計算機視覺中，常用邊緣檢測算法主要有拉普拉斯邊緣檢測、基于模板的邊緣檢測和基于方向梯度法進行的邊緣檢測［14］。本文將3 種算法運行結果進行對比分析，發現利用方向梯度法對纖維單元進行邊緣檢測獲得的邊緣更為流暢清晰。

方向梯度法的思想是若邊緣處于梯度方向最大值處，并且預計在沿著邊緣梯度垂直方向出現下一個梯度點，即將圖片看作二維函數，每個x、y 對應1 個函數值，每個像素點均有梯度方向，這樣使邊緣檢測加入方向性，每個像素點均有梯度方向，檢測效果更好［15］。

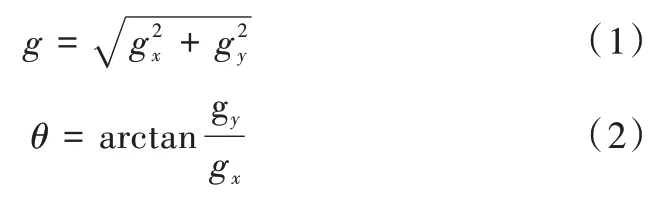
如式（1）所示，gx表示x 方向梯度變化，gy表示y 方向梯度變化，g 表示梯度變化值，θ表示梯度方向。利用方向梯度法對去掉背景后的粘連單元進行邊緣檢測得到邊緣，為了增加邊緣連貫性，對得到的邊緣圖進行膨脹，膨脹后的邊緣檢測結果如圖7（a）所示，放大后結果如圖7（b）所示。

Fig.7 Edge detection results圖7 邊緣檢測結果

2.2 基于連通域的數量檢測

連通域是基于圖像二值化進行的。在圖像分割中，圖像投影釋放出潛在和有用信息。圖像分割方法應用包括背景分離、故障識別、疾病預測、基于內容的圖像檢索、目標識別等。數字圖像分割是檢測和識別給定圖像中目標的關鍵環節［16］，大多將圖像進行二值化，即圖像中像素只有兩種可能，一般默認為非黑即白。利用種子算法將二值化后的圖像進行連通域檢測，最終對連通域進行計數得到連通域數量，即待測纖維粘連單元個數［17］。

二值圖像指圖像中的每個像素只有兩種可能的取值或灰度等級狀態，通常用黑白、B＆W表示。圖像二值化是對圖像進行數據處理和壓縮的過程，通過設置閾值，將像素值劃分為兩部分，分別賦予兩個固定的像素值，一般設置成非黑即白，即二值化后的圖像像素值只有0 和255兩種，二值化后的圖像可反映圖像整體和局部特征，有利于在對圖像進一步處理時，不再涉及像素多級值，簡化處理過程。本文進行圖像二值化時將纖維單元點亮度值標記為255，非纖維單元點亮度值標記為0［18-19］。

二值化后的圖像需進行連通域標記，連通域標記采用區域增長算法［20］。首先，從圖像的第1 個像素點開始遍歷，找到第1 個像素值為0 作為種子點；然后遍歷種子點周圍的點，看像素值是否為0，如果為0，則將其合并到種子像素集合中；最后將集合所有像素作為新的種子像素，如此反復，直到再沒有像素可被合并。在遍歷過程中所有遍歷過的像素均被標記，此時種子像素所在整體構成1 個連通域，然后繼續遍歷其他沒有標記過的像素，找到新的種子點，最終找到所有連通域。

將邊緣檢測得到的邊緣圖和去除背景后的圖像進行做差，可以得到分離的纖維單元，為了獲取更高精度的結果，對做差圖進行腐蝕，防止某些區域有細微連通，得到分離的纖維單元如圖8（a）所示，圖8（b）為左圖中的局部區域的放大顯示。

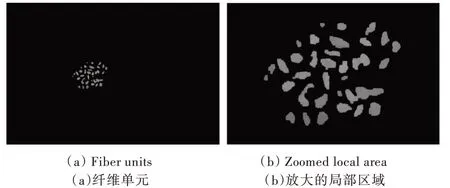
Fig.8 Separated fiber units圖8 分離的纖維單元

對做差得到的纖維單元圖進行數量檢測，數量檢測結果如圖9（彩圖掃描OSID 碼可見）所示，每個紅色框標識檢測出的1 個連通域，對該圖像進行計數得到的纖維單元個數為36，檢測結果為33，除個別單元粘連嚴重以外，大多數纖維單元均可檢測，即使亮度較暗的纖維單元也可被全部檢測出來。

Fig.9 Quantity test result of fiber units圖9 纖維單元數量檢測結果

3 實驗結果與對比分析

3.1 實驗結果

采集尺寸為5 472×3 648 的纖維圖像作為實驗數據。通過對纖維單元進行人工計數作為檢驗數據。實驗過程中，一共選取10 幅圖像進行檢測，10 幅圖像相機位、相機參數固定，其纖維單元大小形狀等有微小差異，但并不會影響檢測效果。

在實驗過程中，為了獲取純凈的纖維單元，采用波段運算的方法去除背景，通過分析多幅圖像RGB 波段圖像，最終確定通過綠光波段和藍光波段做差，然后過濾較低亮度的暗像元以去除纖維單元背景。為了將粘連單元分離開來，本文采用方向梯度法進行邊緣檢測，將去除背景的纖維圖像與檢測到的邊緣做差，以達到去除粘連單元邊緣的目的，從而將粘連單元分離，然后利用連通域標記算法進行纖維單元數量檢測。從檢測結果可以看出，所有纖維單元均可被提取出來，包括亮度值較暗的纖維單元，整體檢測結果檢測誤差較小，僅極個別纖維單元在做差后存在粘連現象。

目前進行粘連單元分離的方法主要有兩種：①對圖像進行銳化，通過調節對比度等方法使單元邊緣弱化，中心較亮的部分突出，但是該方法只適用于邊緣和粘連單元亮度值有明顯差異的圖像，且不適用于粘連單元本身亮度值分布不均勻的情況；②對圖像進行分割，主要方法是分水嶺算法，目前對分水嶺算法的研究較多，但是分割不完全和過分割問題始終沒有得到解決，而且大多數算法研究對象僅為部分粘連單元，對于粘連嚴重的單元始終沒有很好的分割方法。

進行粘連單元數量檢測的關鍵是將粘連單元分成獨立的連通域，然后對所有連通域進行計數，最終得到的數量即為粘連單元個數。為把粘連單元變為獨立單元可將粘連的模糊邊緣變清晰，從而使粘連單元分離開來。本文基于該思想直接進行邊緣檢測，將邊緣提取后去除，從而分離粘連單元。本文利用已發展較成熟的邊緣檢測算法，針對被檢測物體粘連程度較高的特點，采用方向梯度法進行邊緣檢測，同時沿x、y 方向邊緣進行檢測，最后對檢測結果進行合成。方向梯度法是基于物體與背景間灰度或紋理特性上某種不連續性或突變型的一種檢測技術，通過對亮度值發生突變的區域檢測得到邊緣，可有效獲取邊緣信息，對于不發生突變的暗像元區域不會發生誤判，還可完整檢測出粘連程度嚴重的整個區域邊緣，實驗中檢測多幅圖像均獲得了完整的邊緣。通過將粘連單元前景圖減去其邊緣檢測結果可得到獨立的檢測單元，最后基于連通域標記的算法對纖維單元進行數量檢測。

3.2 對比分析

本文提出的粘連單元數量檢測方法在對粘連單元分割研究的基礎上，針對傳統分水嶺圖像分割缺點，對圖像分割進行有效優化。

傳統圖像分割方法基于分水嶺算法。該算法將圖像中的邊緣轉化成“山脈”，將均勻地區轉化為“山谷”，其基本思想是把圖像看作是測地學上的拓撲地貌，圖像中每一點像素灰度值表示該點海拔高度，每一個局部極小值及其影響區域稱為集水盆，而集水盆邊界則形成分水嶺。分水嶺算法根據找到兩個局部極小值區域的交界線求得邊界，所得邊緣是一條由極大值點組成的連貫曲線。但是在實際生產生活中，物體之間的粘連并不是簡單的一條線，往往是由很多最大值點組成的帶狀結構，此時利用分水嶺算法進行邊緣檢測無法找到可連成線的極大值點，因此無法得到準確的邊界檢測結果。

本文提出基于方向梯度法的邊緣檢測算法，圖像像素值變化情況可由像素值分布梯度反映，給定連續的圖像f（x，y），其方向倒數在邊緣方向上取得局部最大值。圖像中1 點邊緣被定義為1 個矢量，模為當前點最大的方向導數，方向為該角度代表的方向。通常只考慮模大小而忽略其方向，但實際情況中邊緣一般是連續變化的點。分水嶺算法可求取兩個局部最小值中間的極大值點（標記為邊界點），但實際生產中邊界往往不是由點連成的線，而是細長的條帶狀結構，所以該方法在實際生產中并不適用。利用方向梯度法相對于分水嶺算法進行的邊緣提取既可兼顧像素點變化大小又能考慮像素點方向變化，從而提高邊緣檢測準確度。

4 結語

本文采用方向梯度法進行邊緣檢測，該方法是目前公認的可較好獲取圖像邊緣的檢測算法。但目前進行粘連單元數量檢測時大都采用將粘連單元分割開來再計數的方法，分割算法僅針對粘連程度較輕且邊界清晰明顯的圖像有較好的分割效果，運用現有算法處理粘連程度較嚴重的圖像時存在嚴重的過分割或分割不足等問題，往往產生較大的影像。實驗證明，本文方法可有效解決過分割或者分割不足的問題，精確分離后的計數誤差在10%以內，效果有明顯改進，在工業生產質檢中具有較強的實用性。

為了將粘連單元分離，本文采用邊緣檢測法，但是該方法僅適用于單元不太小的情況，如果粘連單元太小，則去掉邊緣后單元在濾波過程中可能被過濾掉，因此在盡可能保證邊緣檢測效果好的情況下，如何保證較小粘連單元不被過濾掉，是下一步研究內容。