指數平滑法在鐵路運輸指標預測分析中的應用

馬 力 杭良文 中國鐵路上海局集團有限公司南京東機輛段

1 研究背景

在鐵路運輸管理中，各級領導經常會要求統計部門提供在未來一段時間內運輸指標完成情況預測，以便領導在調整運力、技術改造、新線建設等決策時參考。影響鐵路運輸指標完成情況的因素較多，例如：宏觀經濟政策、工業生產景氣程度、節假日、天氣變化、春運、學生客流等，這些因素包含長期趨勢影響、季節性變化、隨機性等變化特點，數據變化復雜不能簡單用公式描述。對于運輸數據預測擬合，是數據分析的重要目的之一，也是運輸數據發展趨勢預測的重要手段。傳統的時間序列數據分析模型較多，本文主要針對指數平滑法模型在擬合鐵路運輸數據的作用效果進行研究。

2 分析模型

指數平滑法是分析數據的常用方法。主要分為單參數指數平滑法、雙參數指數平滑法等。本文分別使用兩種方法進行分析。為了更好評價數據擬合結果的優劣，定義評價指標平均誤差比例、估計標準誤差。

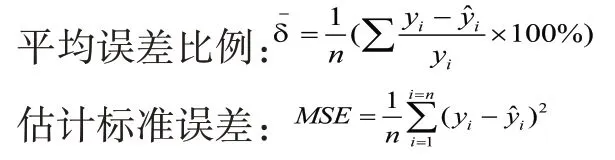
2.1 單參數指數平滑模型

單參數指數平滑法是將一段時期的預測值與實際值的線性組合作為i+1期的預測值，其預測模型為：

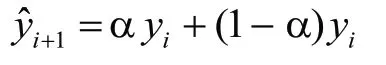
式中，yi表示第i期的實際值；表示第i期的一次指數平滑值（預測值）；a表示平滑系數（0＜a＜1）。

2.2 雙參數指數平滑模型

雙參數指數平滑法又稱Holt 方法，常見的雙參數指數平滑法有加法模型和乘法模型。乘法模型可以看成是在加法模型基礎上取對數，所以乘法模型是加法模型的特殊形式。本文選用加法模型，得到雙參數指數平滑法計算公式為：

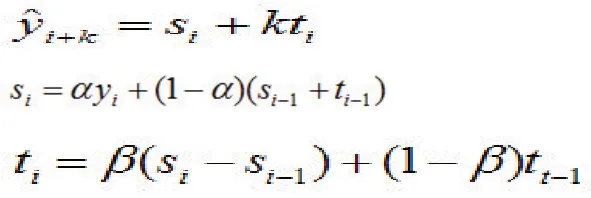
3 數據預測分析

3.1 鐵路運輸數據特點分析

如圖1所示為南京東機務段2017年-2019年全段機車總走行數據變化。機車總走行是反映運輸工作量的基本指標之一，也是反應各類運用機車本務走行公里與輔助走行公里之和的重要數據。從圖中可以看出，機車總走行數據主要有長期趨勢變化、季節性周期波動以及隨機性變化的特點。從長期來看，南京東機務段機車總走行公里呈上升趨勢，主要是因為長三角地區人口居住密集、工業基礎較好、商品貿易發達，受到地方經濟輻射，市場需求較大，鐵路線路里程不斷增加，鐵路運輸量不斷增加。運輸數據季節性波動主要體現在每年2 月（春運）、9 月（學生開學季）以及10 月（國慶黃金周）會出現運輸高峰，而在每年4月、6月、11月運輸數據則相應較低，進入運輸淡季。此外受到市場經濟波動和國家政策調整的影響（例如：鋼鐵去產能、煤炭減產等），運輸數據也存在一定隨機性變化。

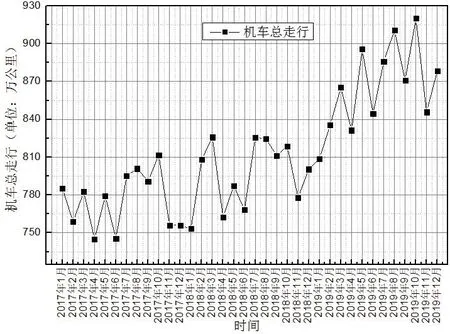
圖1 2017年—2019年機車總走行數據變化

3.2 單參數指數平滑法分析

單參數指數平滑法是對時間序列數據由近及遠采取具有逐步衰減性質的加權處理。每一期預測值都是上一期實際值與預測值的加權平均。其權數由近及遠按照幾何級數的衰減，特點是近期權數較大，遠期權數較小。加權系數符合指數規律，又具有平滑數據的作用。但是不能區分長期趨勢和季節變化，而是將長期趨勢、季節變化 、隨機變化等因素都看成一個整體進行處理。

使用指數平滑法時數據處理的關鍵是確定一個合適的平滑系數，本文對平滑系數分別取0.2、0.5、0.8 工況下，分別擬合機車總走行數據，得到結果如圖2 所示。從圖中可以看出不同指數平滑系數下，都能對機車總走行數據進行擬合且與實際值間都存在一定誤差。同時，隨著平滑系數增加，數據波動性越弱，數據衰減較強。

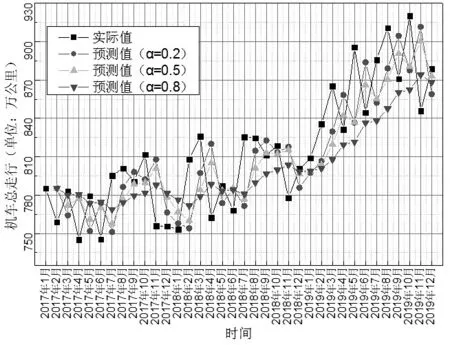
圖2 不同平滑系數下單參數指數平滑預測值與實際值對比

為了具體分析不同平滑系數a情況下數據擬合的效果，對不同平滑系數a情況下實際值與預測值間的平均誤差比例、估計標準誤差進行計算，將數據匯總得到表1。

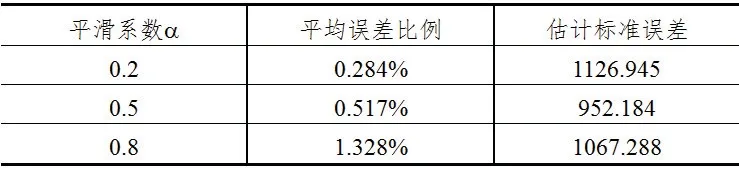
表1 不同平滑系數a下的誤差情況

從表1 可以看出，當平滑系數a=0.5 時估計標準誤差最小，當平滑系數a=0.2 時平均誤差比例最小。考慮平均誤差比例是每一期誤差比例的平均數，平均數易受到極值影響，不如估計標準誤差更具有統計學的穩定性。所以認為估計標準誤差小的平滑系數更佳。如果平滑系數取值接近1 時，數據變化幅度較大適用于時間數列數據變化劇烈的情況，以便很快跟隨其變化。取值接近0 時，則各期數據的作用緩慢減弱，呈比較平穩的狀態。而運輸數據的變化具有長期趨勢增加、短期波動較大的特點，則不能反應數據的波動性。在實際應用中擬合機車總走行數據，平滑系數的取值需要反復比較確定，數值偏大或偏小都會增加估計標準誤差。

通過EXCEL規劃計算，當平滑系數取值0.61時平均誤差比例和估計標準誤差分別為0.692%、934.7，此時計算得到的各期預測值與實際觀測值之間的誤差最小，效果最佳。平滑系數的取值直接影響過去各期數據對預測值的作用，當使用單參數指數平滑法時近期數據作用最大，遠期各數據的作用迅速衰減，所以單參數指數平滑法適合短期數據預測，預測數據期數越多準確性越低。

3.3 雙參數指數平滑法分析

雙參數指數平滑法將數據的影響因素分解為“平滑值+趨勢值”，然后通過對數據的平滑值和趨勢值分別進行加權處理。由于兩個參數加權作用，數據衰減程度不會較快遞減，避免了單參數指數平滑法中近期權數較大遠期權數較小情況，強化了數據平滑的作用。

使用指數平滑的關鍵點是：①初始平滑值和趨勢值的確定，②確定兩個合適的平滑系數a、β。如果確定的平滑值和趨勢值不能很好的代表數據特點，后期的數據發展趨勢會偏離實際值。平滑系數a、β代表后期數據的衰減和加權變化，其特點是反應季節變化和趨勢變化的影響因子在數據發展中所占的加權比例。對于初始平滑值和趨勢值的處理，常規做法是運用線性方程法確定數據的初始平滑值和趨勢值。因為回歸方程的特點就是利用最小二乘法對參數進行估計，擬合的平滑值和趨勢值保持偏導數為零的特點。本文也采用回歸方程法確定初始平滑值和趨勢值。而對于平滑系數a、β 處理，采用枚舉法確定。利用EXCEL 進行規劃求解，以估計標準誤差最小為主要目標，查找分析最佳的平滑系數a、β 取值。通過計算發現當a=0.082，β=0.013 時，此時平均誤差比例和估計標準誤差分別為0.223%、735.89，估計標準誤差達到最小值。雙參數指數法預測值和實際值對比結果如圖3所示，預測值過濾了一定的隨機波動，使得數據結果更加平滑，同時也能反應出數據的季節變化和長期趨勢變化的特點。

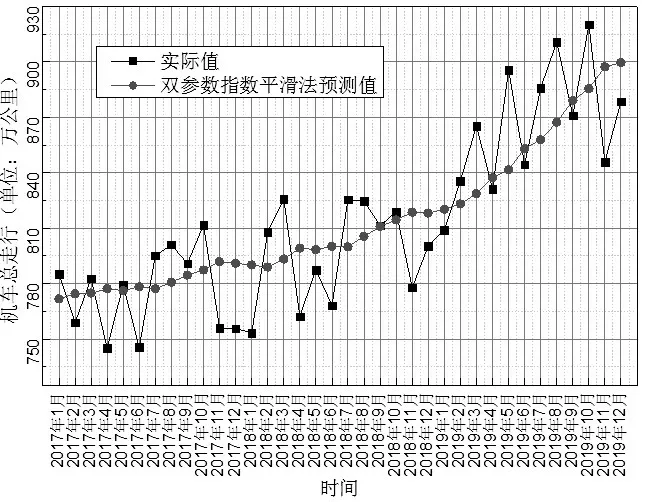
圖3 雙參數指數平滑預測值與實際值對比

3.4 結果對比

針對本文涉及的兩種指數平滑法，分別取估計標準誤差最小時的預測數據，將主要評價指標對比得到表2。

從表2可以看出雙參數指數平滑法預測結果比單參數指數平滑法預測結果的誤差更小。單參數指數平滑法通過擬合使得數據中短期偶然性因素的影響被削弱，從而顯示出數據在較長時間的基本發展趨勢。對預測結果的準確性會隨著期數增加逐級降低，使得觀察值離預測值時期越久遠權數變得越小，雙參數指數平滑法其基本原理是把具有長期趨勢、季節性變化的時間序列進行分解，通過數據處理可以過濾掉隨機波動的影響。雙參數指數平滑法克服了單參數指數平滑法不能區別長期趨勢和循環變動的缺點，也解決了一個參數權數比重逐漸變小的問題。所以從預測結果看雙參數指數平滑法比單參數指數平滑法更好，更適合鐵路運輸指標預測分析。

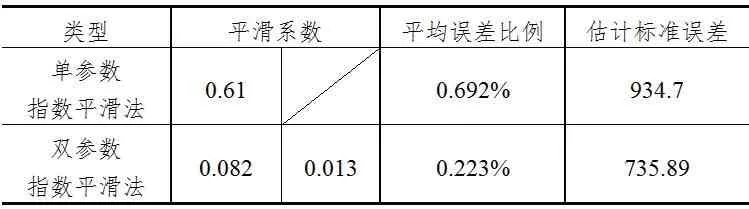
表2 單參數和雙參數指數平滑法的誤差情況對比

4 結論

通過單參數和雙參數指數平滑法模型在預測鐵路運輸數據的作用效果進行研究分析，得到的結論有：

（1）指數平滑法可以過濾數據隨機性變化，使得預測數據能夠在一定誤差范圍內反應周期性（季節性）和長期趨勢變化特點。

（2）單參數指數平滑法在預測數據時，數據期數越多衰減越大準確性降低，不適合長期預測。

（3）雙參數指數平滑法在預測數據時，可以分解平滑值和趨勢值，通過兩個參數加權作用使數據變化更加平滑，降低數據衰減帶來的誤差，更貼近實際值。

（4）通過兩種方法對鐵路運輸數據的擬合，從誤差結果分析，雙參數指數平滑法更適合用于數據的預測分析。