典型壓水堆堆芯物理-熱工耦合穩態計算軟件的開發與驗證

李治剛，安 萍，潘俊杰，盧 川，蘆 韡,*，楊洪潤

(1.中國核動力研究設計院，四川 成都 610213； 2.核反應堆系統設計技術重點實驗室，四川 成都 610213)

在壓水堆中燃料溫度、慢化劑密度、冷卻劑溫度等熱工參數會影響中子的截面，進而影響堆芯中子通量和功率分布，而功率又反過來影響堆芯燃料溫度、冷卻劑溫度等熱工參數，即壓水堆中子物理與熱工之間存在強烈的反饋現象[1]，因此目前在壓水堆的設計和安全分析中均須考慮物理-熱工耦合計算，以便更加真實地模擬堆芯穩態和瞬態過程。自20世紀80年代以來，國內外針對壓水堆物理-熱工耦合現象開展了大量研究，提出了較多有效的耦合計算方法，如Picard迭代法[2]、JFNK迭代法[3]，并研發了大量三維物理-熱工耦合計算軟件，如CRONOS/FLICA4、PARCS/TRACE[4]、CSSS[5]、DYN3D/ATHLET[6]、NALSANMT/CORBA-Ⅳ[7]等。

目前典型的堆芯物理-熱工耦合計算程序常采用外耦合方式實現，且常采用1種中子物理或熱工水力計算方法求解守恒方程。為研究不同中子物理、熱工水力計算方法對壓水堆物理-熱工耦合計算的影響，本文通過內耦合方式實現物理-熱工耦合計算，研制典型壓水堆堆芯物理-熱工耦合計算軟件ARMcc，其中采用節塊展開法(NEM)[8]和格林函數節塊法(NGFM)[9]求解中子擴散方程，分別采用單通道計算模型[10]和一維圓柱導熱計算[11](采用有限差分法或有限體積法求解)冷卻劑溫度和燃料溫度，并采用典型壓水堆耦合基準題NEACRP[12-13]彈棒初始參數對軟件穩態計算功能進行驗證。

1 理論模型

1.1 穩態中子擴散方程求解方法

多群穩態中子擴散方程[14-15]可表達為：

(1)

式中：χg為裂變譜；Dg為第g群中子擴散系數；Σfg′為第g′群裂變宏觀截面；φg為第g群中子注量率；υg′為第g′群平均裂變中子數；Σsg′→g為第g′群到第g群的散射截面；ΣRg為第g群的移除截面；k為特征值或有效增殖因數。

目前式(1)的典型求解方法包括有限差分法、節塊法、有限元方法等，其中節塊法由于具有較高的效率和精度，在商業軟件中被廣泛應用。節塊法的重要特點是對式(1)進行橫向積分，將三維問題的求解變成聯立求解3個一維問題。在網格m內，對給定的坐標方法u(交替等于x,y,z)，對式(1)沿與u方向垂直的另兩個方向v和w進行積分，得到3個一維方程(為便于描述，全文略去節塊編號m)：

g=1,…,G;u=x,y,z;u≠v≠w

(2)

式中，φgu、Qgu和Lgu分別為橫向積分通量、源項(包括裂變源項和散射源項)和橫向泄漏項。

典型的節塊法有NEM、解析節塊法(ANM)和NGFM等，不同節塊法的差異在于φgu、Qgu和Lgu等近似處理方式。本文將采用四階NEM和第二類邊界條件NGFM進行多群穩態中子擴散方程的求解，具體的理論詳見文獻[8-9]。

1.2 熱工水力計算方法

1) 單通道計算模型

冷卻劑單相單通道的守恒方程為：

(3)

式中：ρ為冷卻劑密度，kg/m3；h為冷卻劑焓，J/kg；u為冷卻劑流動速度，m/s；q為體積熱流密度，W/m3。

對式(3)在網格m進行z方向的積分得到：

(4)

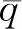
根據入口邊界條件，采用式(4)可依次計算得到每個網格出口焓hout，則網格m的平均焓為:

(5)

2) 一維圓柱導熱模型

一維圓柱導熱穩態模型的守恒方程為：

(6)

式中：λ為導熱系數，W/(cm·℃-1)；T為溫度，℃。

典型的壓水堆燃料元件幾何形式如圖1所示。在徑向上燃料芯體劃分為n個網格，氣隙為1個網格，包殼劃分為2個網格。

圖1 典型壓水堆燃料元件幾何形式Fig.1 Geometry of fuel element in typical PWR

(1) 有限差分法

采用有限差分法(DIF)對式(6)在網格i處進行離散，得到網格i的溫度計算關系式：

(7)

式中：λ為材料的導熱系數；ri為第i個網格的半徑；Δri為第i個網格的間距。關于燃料中心、芯體外表面、包殼內外表面的處理方式參見文獻[16]。

(2) 有限體積法

采用有限體積法對式(6)進行離散，表達形式如下：

(λi-1/2ri-1/2+λi+1/2ri+1/2)·

(8)

式中，ri+1/2和ri-1/2分別為第i個網格左右邊界的半徑。

式(7)、(8)均為三對角矩陣，采用高斯-賽德爾迭代計算得到燃料元件的徑向溫度分布，采用羅蘭公式加權計算燃料有效溫度。

2 驗證與分析

基于上述中子物理和熱工水力計算理論，采用C/C++語言開發了反應堆堆芯多物理耦合計算軟件(ARMcc)。本文分別采用三維LWR基準題[17]和NEACRP-L-335基準題[12-13,18]對程序中子擴散方程求解和物理-熱工耦合計算進行驗證。

2.1 中子擴散方程求解驗證

三維LWR基準題的幾何布置及材料截面參數見文獻[17]。采用NEM和NGFM對三維LWR基準題進行模擬，堆芯有效增殖因數keff結果及偏差列于表1，三維LWR基準題相對功率分布及偏差如圖2所示。

表1 keff結果及偏差Table 1 Result and deviation of keff

由表1和圖2可知，本軟件采用的NEM和NGFM方法模擬三維LWR基準題均具有較高的精度。keff與參考結果相比，NEM和NGFM方法計算的keff偏差均在10 pcm以內；堆芯徑向相對功率與參考結果相比，采用NEM方法的最大偏差為0.553%，采用NGFM方法的最大偏差為1.03%。

圖2 三維LWR基準題相對功率分布及偏差Fig.2 Relative power distribution and deviation of 3D LWR benchmark

2.2 物理-熱工耦合計算驗證

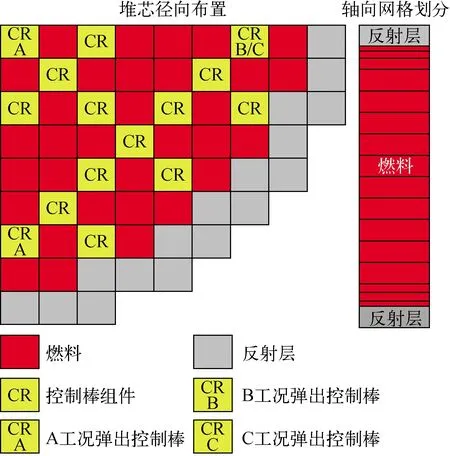
圖3 PWR NEACRP彈棒基準題堆芯模型Fig.3 Core model of PWR NEACRP rod ejection benchmark

NEACRP彈棒基準題是1991年由Finnemann等[12-13]建立的，包含壓水堆和沸水堆兩種堆型，主要用于輕水堆堆芯三維物理-熱工耦合軟件的驗證。其中壓水堆基準題參考了典型壓水堆的幾何尺寸和運行狀態，堆芯布置了157個燃料組件和1圈徑向反射層，軸向分為18層，如圖3所示[18]。根據初始功率水平和控制棒彈出位置的不同，共包含6種工況：A1，1/4堆芯、中心控制棒在熱態零功率(HZP)彈出；A2，1/4堆芯、中心控制棒在熱態滿功率(HFP)彈出；B1，1/4堆芯、外圍1組控制棒在熱態零功率彈出；B2，1/4堆芯、外圍1組控制棒在熱態滿功率彈出；C1，1/2堆芯、外圍1組控制棒在熱態零功率彈出；C2，1/2堆芯、外圍1組控制棒在熱態滿功率彈出。

關于NEACRP基準題幾何尺寸劃分及材料截面參數可詳見文獻[12]，基準題的參考結果由PANTHER程序采用精細時空網格計算，在1993年發布初版、1997年發布修訂版，計算結果包括穩態和瞬態關鍵結果參數。本文將采用1997年修訂版的穩態計算結果對本軟件物理-熱工穩態耦合計算模塊進行驗證，而對于PANTHER未提供的結果參數(如堆芯組件徑向功率分布等)將采用PARCS軟件計算結果作為參考。2種物理計算方法和2種熱工計算方法組合后形成4種計算模式(NEM+VOL對應節塊展開法和有限體積法，NEM+DIF對應節塊展開法和有限差分法，NGFM+VOL對應格林函數法和有限體積法，NGFM+DIF對應格林函數法和有限差分法)。

1) 臨界硼濃度

采用ARMcc針對NEACRP基準題計算的臨界硼濃度對比結果列于表2。與PANTHER(1997)相比，4種模式計算的6種工況的臨界硼濃度與參考結果符合較好，最大相對偏差在0.5%以內，其中在A2和C2工況中，NEM方法計算臨界硼濃度的精度高于NGFM方法，而在剩余4個工況中，NGFM方法計算臨界硼濃度的精度高于NEM方法。

2) 堆芯組件徑向相對功率最大值

徑向相對功率最大值Fxy,max列于表3。與PARCS結果相比，ARMcc計算的堆芯組件徑向相對功率最大值與參考結果符合較好，相對偏差在0.5%以內。采用NEM方法計算的最大相對偏差-0.39%出現在A2算例中，而采用NGFM方法計算的最大相對偏差0.27%出現在C2算例中。采用有限體積法或有限差分法對Fxy,max的影響較小。

B1算例堆芯組件徑向功率分布如圖4所示，其中在同一種物理方法中采用VOL和DIF的相對功率分布基本相同。從圖4可知，相對功率<0.9的組件功率最大偏差情況為：NEM方法為2.09%，NGFM方法為-0.14%，相對功率>0.9的組件功率最大相對偏差情況為：NEM方法為-1.48%，NGFM方法為-0.06%。

表2 不同工況下的臨界硼濃度Table 2 Critical boron concentration of different cases

表3 不同工況下的堆芯組件徑向相對功率最大值Table 3 Maximum radial relative power of core assembly of different cases

圖4 B1算例堆芯組件徑向功率分布(1/8堆芯)Fig.4 Radical power distribution of B1 case (1/8 core)

3) 堆芯軸向相對功率最大值

堆芯軸向相對功率峰值Fz,max列于表4。與PARCS結果相比，4種計算模式得到的堆芯軸向相對功率最大值與參考結果符合較好，最大相對偏差不超過0.1%。采用NEM+VOL模式計算時在滿功率工況A2、B2和C2中相對偏差達到最大，為0.1%。

4) 堆芯燃料最高溫度

表5列出不同工況下的堆芯燃料最高溫度。與PARCS結果相比，因零功率算例(A1、B1和C1)堆芯功率較小，燃料最高溫度與初始溫度相同，相對偏差為0.0%；在滿功率算例中，不同計算模式得到的燃料最高溫度存在明顯差異：1) 采用相同物理計算方法時，采用有限體積法得到的燃料最高溫度低于采用有限差分法；2) 采用相同熱工計算方法時，NEM方法計算的結果低于NGFM方法；3) NEM+VOL模式相對偏差最小(B2算例中為0.77%)，NGFM+DIF模式相對偏差最大(C2算例中為1.33%)。

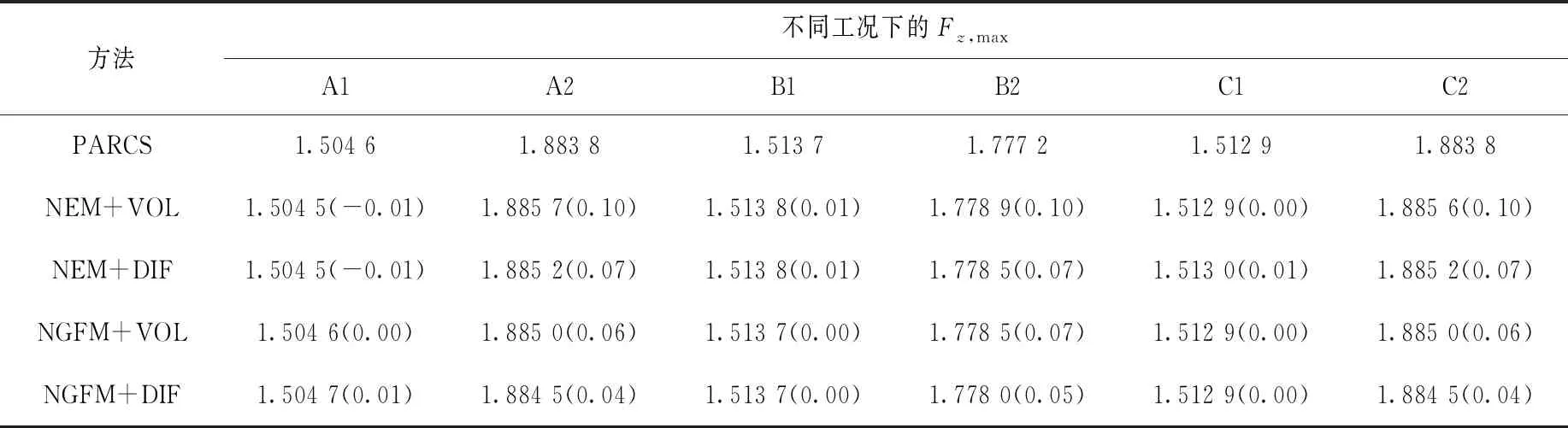
表4 不同工況下的堆芯軸向相對功率峰值Table 4 Core axial relative power peak of different cases

表5 不同工況下的堆芯燃料最高溫度Table 5 Core maximum fuel temperature of different cases

5) 堆芯燃料多普勒溫度

堆芯燃料多普勒溫度影響中子截面參數，表6列出不同工況下的堆芯燃料多普勒溫度。與PARCS結果相比，零功率算例相對偏差為0.00%；在滿功率算例中，4種計算模式的最大相對偏差在0.5%以內，有限差分法較有限體積法更接近參考結果。

6) 堆芯出口冷卻劑最高溫度

堆芯出口溫度體現了熱量在軸向上的積分效果。堆芯出口冷卻劑最高溫度列于表7。與PARCS結果相比，零功率算例相對偏差為0.00%；在滿功率算例中，4種計算模式的最大相對偏差在0.2%以內，而NGFM方法的相對偏差小于NEM方法的，更接近參考結果。

表6 不同工況下的燃料多普勒溫度Table 6 Core fuel Doppler temperature of different cases

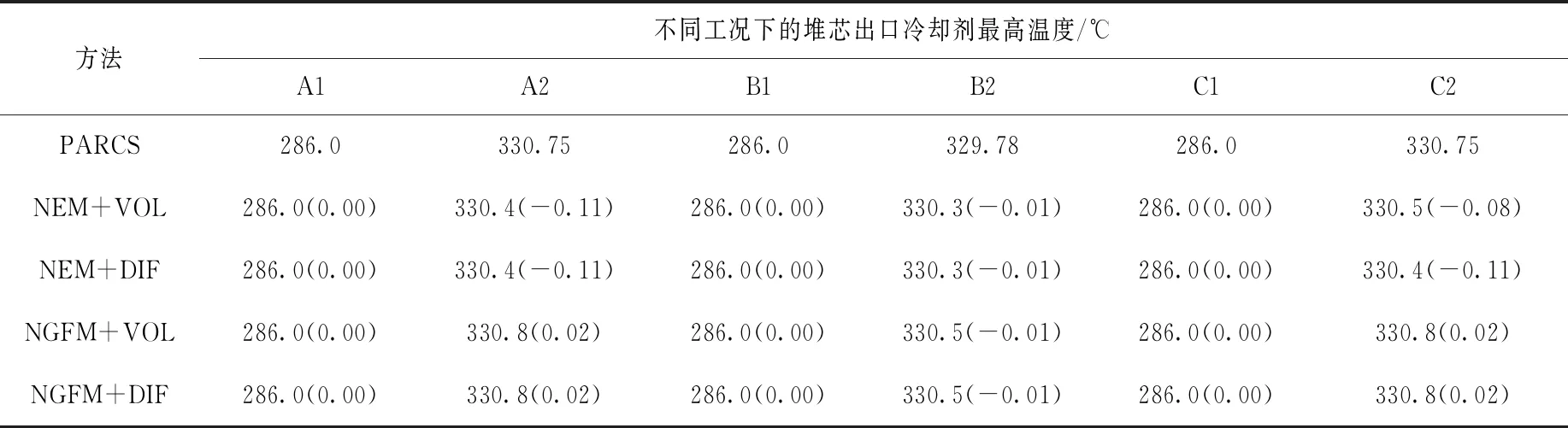
表7 不同工況下的堆芯出口冷卻劑最高溫度Table 7 Maximum temperature for core coolant outlet temperature of different cases

3 結論

本文針對壓水堆堆芯物理-熱工耦合計算現象，基于2種典型節塊法和一維圓柱導熱計算方法，研制了堆芯物理-熱工耦合穩態計算程序，采用三維LWR基準題對中子物理求解模塊進行了驗證，采用LWR彈棒基準題NEACRP-L-335的穩態結果對物理-熱工耦合穩態計算模塊進行了驗證，分析了中子物理、熱工水力計算方法對物理-熱工耦合計算的影響，得到如下結論。

1) 采用NEM方法和NGFM方法在求解中子擴散方程時具有良好的精度，對三維LWR基準題模擬結果與參考結果符合較好。

2) 4種計算模式均能較為準確地模擬堆芯物理-熱工耦合過程，但不同計算模式對關鍵參數的影響程度不同：對堆芯出口溫度和堆芯軸向相對功率最大值的影響較小，對堆芯臨界硼濃度、堆芯燃料最高溫度和堆芯多普勒溫度影響較大。

3) NGFM+DIF模式能更加準確地模擬堆芯燃料多普勒溫度和堆芯功率分布；NGFM+VOL模式能更加準確地模擬臨界硼濃度；NEM+VOL能更加準確地模擬堆芯燃料最高溫度。