VVER機組LBLOCA始發嚴重事故工況下堆芯出口溫度BEPU分析

陳仁宗，王 輝，孫曉暉

(1.清華大學 核能與新能源技術研究院，北京 100084；2.中國核電工程有限公司，北京 100840)

1988年，美國核管會(NRC)修訂了美國聯邦法規10CFR50.46允許使用最佳估算方法進行大破口事故的認證級分析，但必須考慮不確定性，并加以量化計算，以保證分析結果在驗收準則之內具有較高的概率[1-4]。最佳估算方法應符合以下3個條件：應根據選定的驗收準則，事故分析不引入有意的悲觀性；使用最佳估算程序；包含不確定性分析[5]。最佳估算方法利用盡可能詳細的模型而非簡單模型來保證結果更為接近物理現實，用最佳估算結果的不確定性來量化分析結果與物理現實之間的差距[6]。

目前，最佳估算加不確定性(BEPU)方法主要應用于設計基準事故的安全分析[7-9]。與設計基準事故相比，嚴重事故現象更加復雜，涉及堆芯裸露升溫、燃料包殼氧化升溫失效、堆芯熔毀和裂變產物釋放等諸多過程。復雜的嚴重事故現象導致了嚴重事故更大的不確定性和更為復雜的不確定性分析計算過程。嚴重事故現象復雜，其不確定性較大，目前尚無官方發布的嚴重事故現象識別排序(PIRT)表。本文采用的方法是結合設計基準事故PIRT表中參數和與嚴重事故現象相關的參數進行嚴重事故輸入參數的不確定性分析。

堆芯出口溫度(CET)是核電廠安全運行的重要監測參數，在嚴重事故管理導則(SAMG)中作為堆芯狀態的重要表征參數，可作為堆芯損傷評價和簡化源項評估的整定值，并可作為嚴重事故管理導則的入口條件。同時，考慮堆芯裸露后復雜的嚴重事故現象，文中并未針對包殼破裂后的嚴重事故進程進行不確定性分析。包殼破裂通常被作為裂變產物氣隙釋放過程的開始，在堆芯損傷評估和簡化源項評估過程中扮演重要的角色。

本文以VVER1000壓水堆核電廠為研究對象，選取大破口失水事故(LBLOCA)始發嚴重事故進行包殼破裂對應堆芯出口溫度的BEPU分析。

1 計算模型

本文以VVER1000壓水堆核電廠為研究對象，BEPU計算流程如圖1所示。第1步，建立VVER1000的最佳估算模型，并對模型進行驗證；第2步，選取不確定性分析的輸入參數，并對輸入參數進行取樣，根據取樣結果進行計算；第3步，整理計算結果，進行不確定性和敏感性分析。

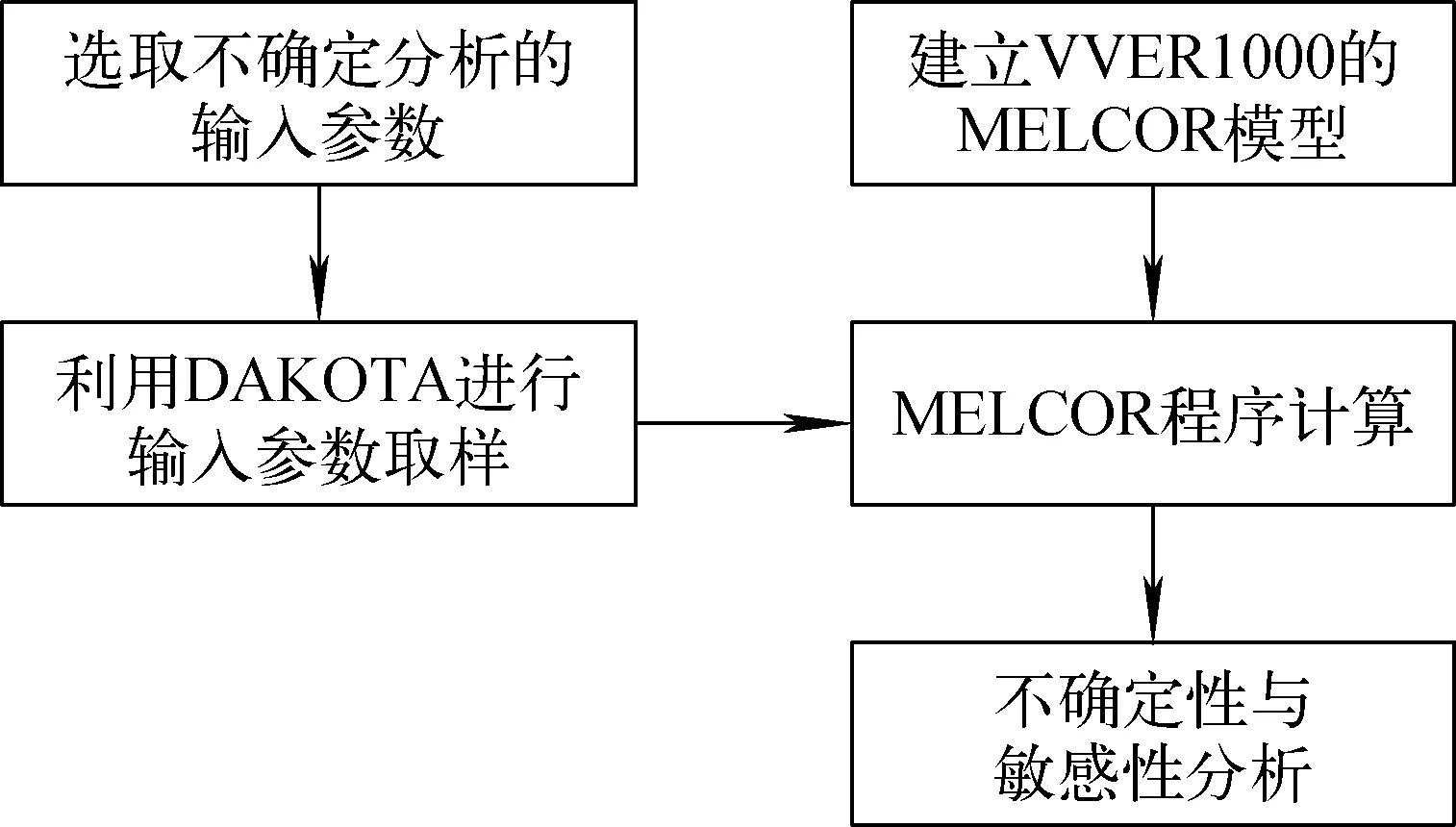
圖1 BEPU計算流程Fig.1 Flowchart of BEPU calculation

本文采用的最佳估算程序為MELCOR。MELCOR是NRC委托桑迪亞國家實驗室開發的用于概率風險評估的程序[10]，主要用于嚴重事故分析，如SAMG中時間窗口的計算、氫氣風險和源項評估等，目前也是監管機構主要的安全評審工具。MELCOR的運行需要兩步，第1步執行MELGEN進行輸入檢查，第2步啟動MELCOR進行迭代計算。

1.1 VVER1000模型建立與瞬態計算

VVER1000壓水堆核電廠是由俄羅斯研發的第3代核電技術[11]。核電廠主回路系統包括4個環路，每個環路有1臺主泵和1臺直流式蒸汽發生器，共用1臺穩壓器。反應堆熱功率為3 000 MW，堆芯出口處壓力為15.7 MPa，入口冷卻劑溫度為291 ℃。采用MELCOR對VVER1000壓水堆核電廠的設計特點建立最佳估算模型，系統節點圖如圖2所示。建模對象包括反應堆壓力容器、穩壓器、直流式蒸汽發生器、主泵、主給水系統和主管道等。其中壓力容器包括下降段、下封頭、下腔室、堆芯區域、旁通段和上腔室的模擬。

在進行瞬態計算前要對模型進行穩態調試，確保模擬值與設計值一致。冷卻劑流量、堆芯入口溫度、堆芯出口溫度、堆芯壓力的模擬值與設計值對比如圖3所示，模擬值與設計值的相對誤差列于表1，由圖3和表1可知，模擬值與設計值之間的誤差較小，相對誤差均在1%以內，說明所建模型可信，可用于進一步的計算。

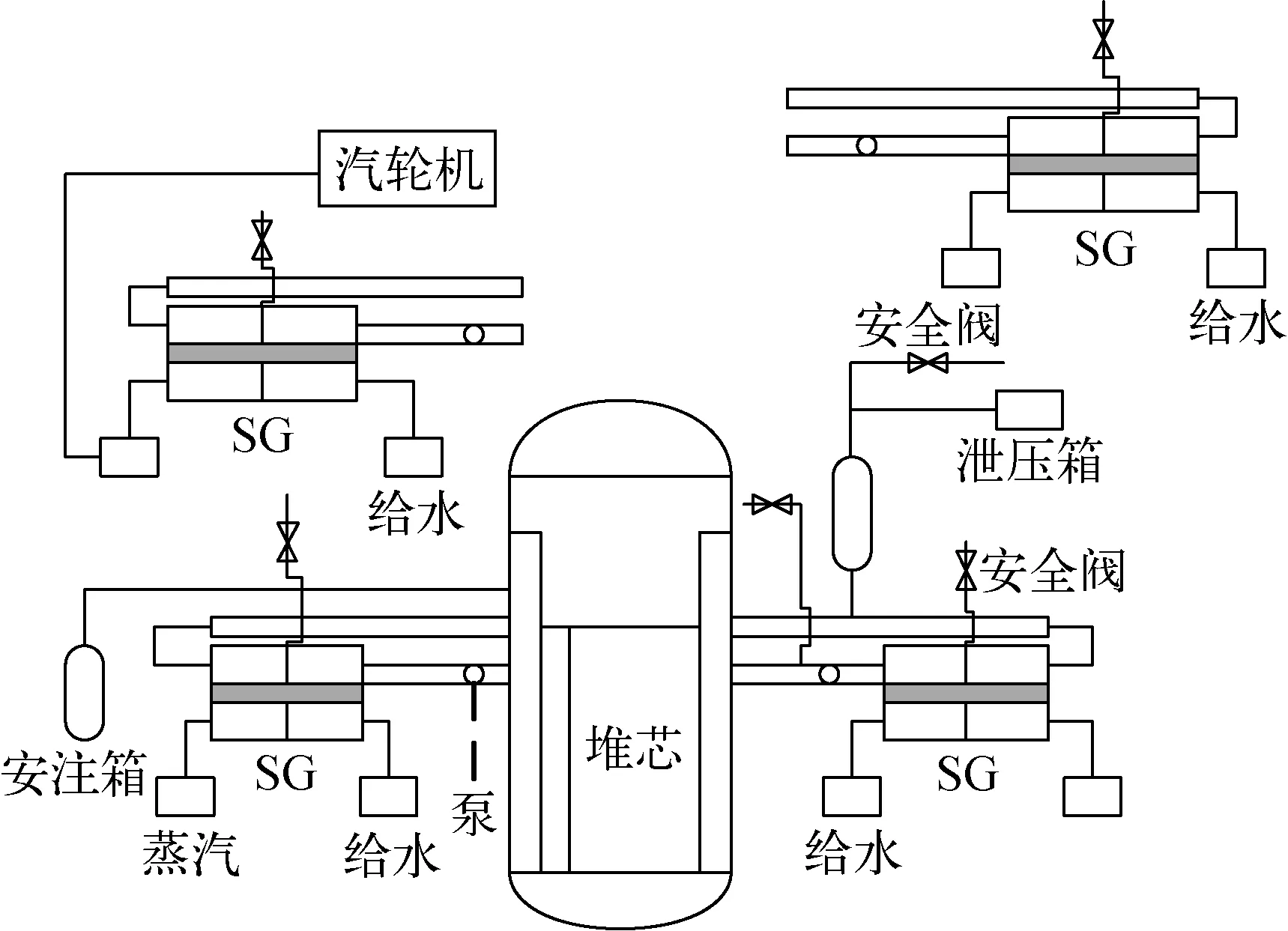
圖2 主回路系統節點圖Fig.2 Node diagram of main circuit system

LBLOCA是輕水堆安全設計的基準事故[12]。國際原子能機構把LBLOCA始發嚴重事故作為計算簡化源項的基準事故[13]，國內及美國NRC將NUREG-1465報告中LBLOCA始發嚴重事故的源項作為核應急的參考源項[14]。本文選取LBLOCA作為始發事故，事故假設條件如下：0 s時刻，反應堆冷管段發生當量直徑為30 cm的破口；余熱排出系統不可用；安注箱的非能動部分可用，能動部分失效；蒸汽發生器二次側輔助給水喪失。

事故發生后，大量冷卻劑泄漏至安全殼內，導致安全殼內壓力升高，同時一回路壓力迅速降低，從而觸發反應堆緊急停堆及主泵停運。壓力降低到一定值時，安注箱非能動部分開始向堆芯注水，隨著應急冷卻水的不足，堆芯開始裸露升溫，然后包殼破裂，開始氣隙釋放。大破口失水事故序列列于表2。

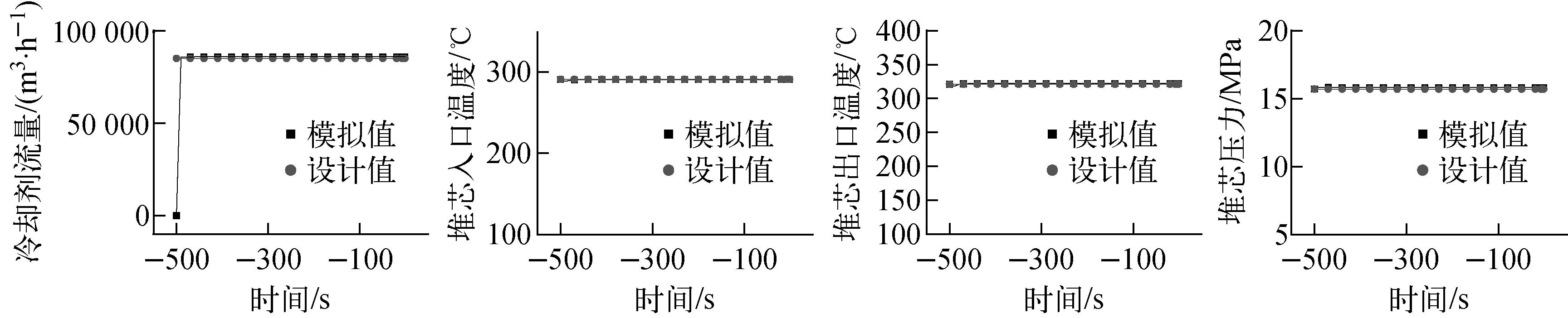
圖3 不同參數的模擬值與設計值對比Fig.3 Comparison of simulation value and design value of different parameters

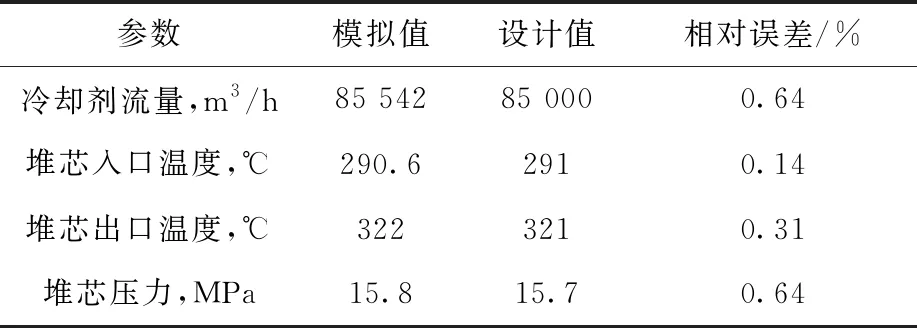
表1 模擬值與設計值的相對誤差Table 1 Relative error between simulation value and design value

表2 事故序列Table 2 Accident sequence

1.2 不確定性分析方法

本文采用拉丁超立方抽樣方式對輸入參數進行抽樣。與簡單隨機抽樣相比，拉丁超立方抽樣具有更高的抽樣維度，抽取的樣品參數更具代表性。拉丁超立方抽樣的實現步驟如下：1) 將參數按其范圍進行等概率劃分，劃分為很多子范圍；2) 用隨機數產生器產生指定數量的[0，1]范圍內的隨機數；3) 根據均勻分布或正態分布將隨機數映射為實際范圍內的參數。

本文采用Wilks非參數統計方法[15-16]進行不確定性量化計算，此方法廣泛應用于BEPU統計分析中。其基本思想是通過Wilks公式根據選定的置信水平和概率水平獲取最小的計算次數，通過對響應參數的有序統計理論來獲取統計容忍區間。Wilks公式為：

β=1-γN

(1)

式中：β為置信水平；γ為概率水平；N為計算次數。

基于Wilks公式，對于單側統計容忍限值(95/95)，樣本數決定了限值的選取原則：樣本為59組，則許用限值為59組計算結果的最大值；若樣本為93組，則許用限值為93組計算結果中的第2大值；若樣本為124組，則許用限值為124組計算結果中的第3大值。本文選取的樣本數為59。

2 輸入參數選取與抽樣

2.1 輸入參數選取

結合用于設計基準事故的LBLOCA PIRT表[17-18]、與鋯包殼破裂相關的嚴重事故現象和專家判斷進行輸入參數的確定。綜合考慮核電廠設計文件、工程經驗判斷和相關文獻資料中的參考值進行輸入參數范圍和概率密度分布的判定。不確定性輸入參數及其范圍、分布列于表3。

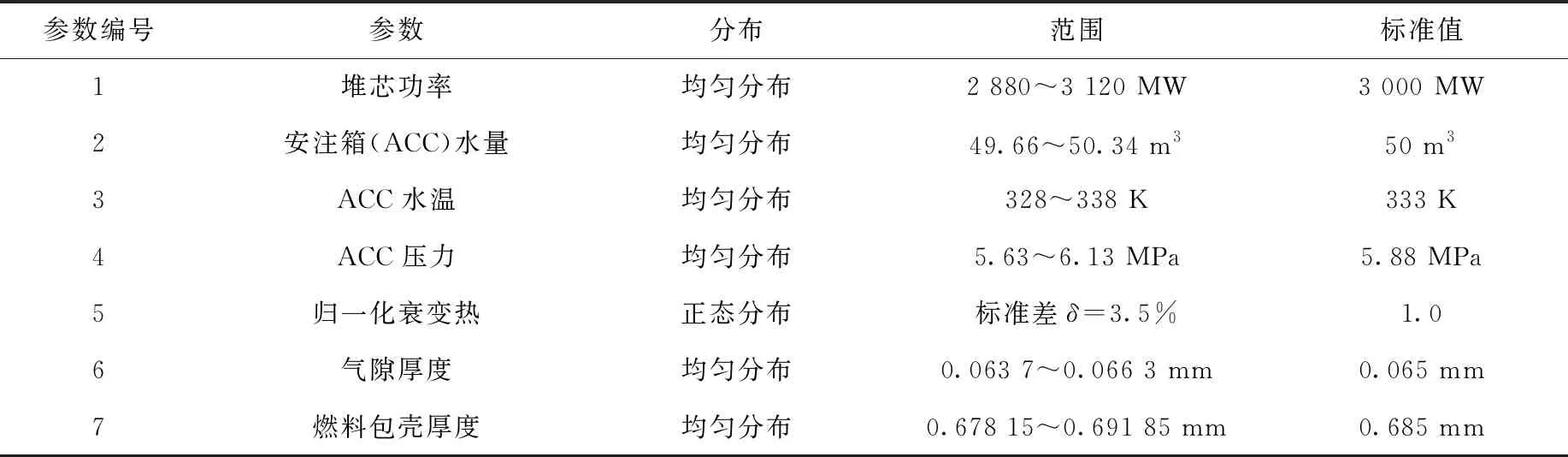
表3 不確定性輸入參數Table 3 Uncertainty input parameter

2.2 輸入參數抽樣

輸入參數的抽樣采用DAKOTA程序[19]實現，選用Mersenne Twister隨機數產生器，種子設定值為98 765。對不確定性輸入參數分別進行59次拉丁超立方抽樣，歸一化結果如圖4所示。

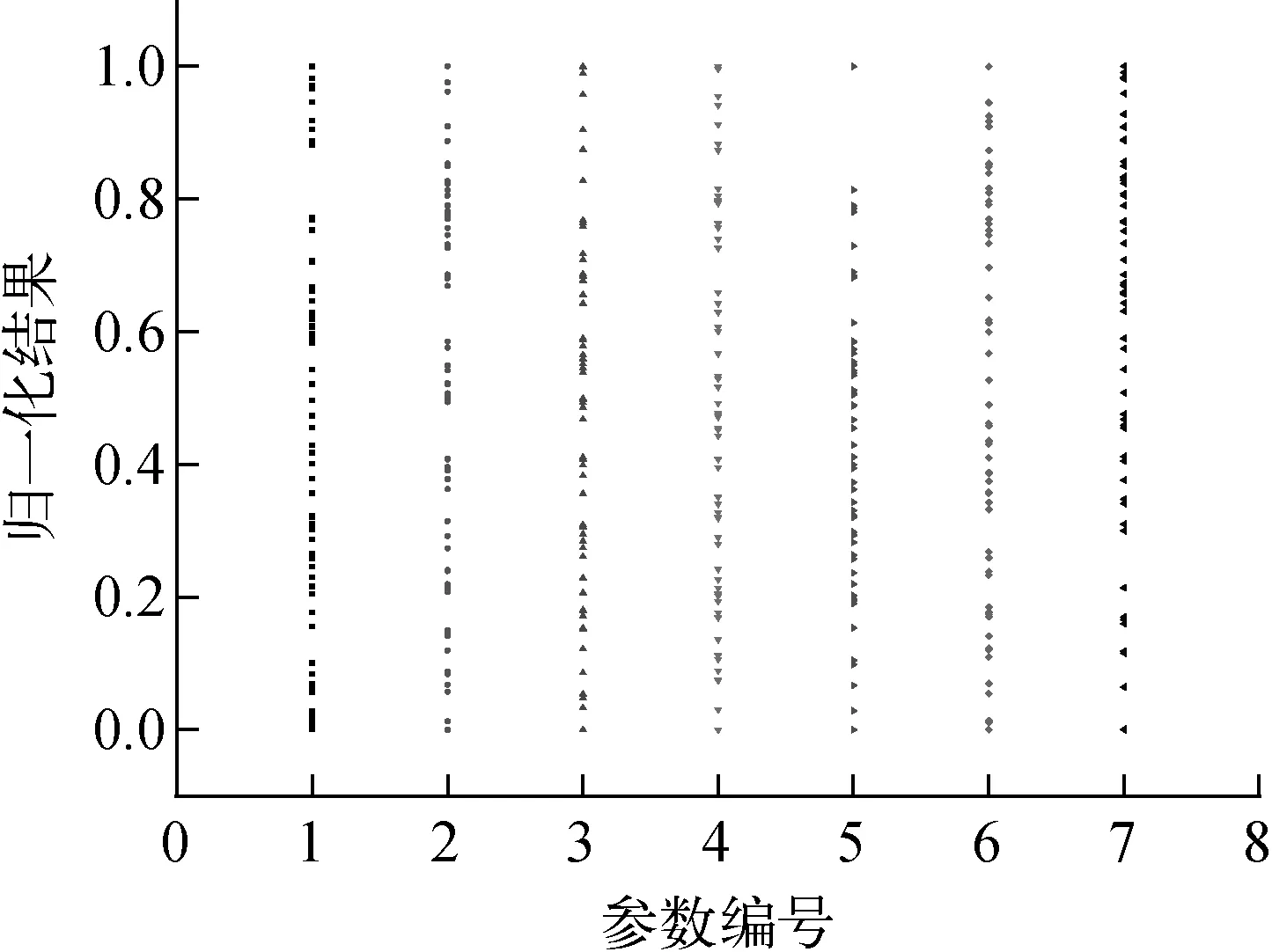
圖4 不確定性輸入參數歸一化分布Fig.4 Normalized distribution of uncertainty input parameter

由圖4可看出，參數的歸一化結果與參數分布形式有關，均勻分布參數的歸一化結果呈現均勻分布，正態分布參數的歸一化結果呈現中間聚集效應。輸入參數抽樣結果達到了預期的效果。

3 結果分析

3.1 不確定性量化

對59組MELCOR計算結果進行分析整理，得到氣隙釋放時間和堆芯出口溫度，如圖5所示。根據Wilks非參數統計方法，對于單側統計容忍限值(95/95)，樣本為59組，則許用限值為59組計算結果的最大值。據此得到的氣隙釋放時間和堆芯出口溫度單側統計容忍限值分別為1 905.71 s和430.85 ℃。

3.2 敏感性分析

Spearman秩相關系數法是全局敏感性方法，可檢驗多個輸入參數對響應參數的全局影響。采用Spearman秩相關系數法作為輸入參數對堆芯出口溫度敏感性進行分析，相關系數取值范圍為[-1，1]，絕對值的大小表示敏感性的強弱；數值的正負號表示正負相關性，正號表示正相關性，負號表示負相關性，零表示不相關，其表達式如式(2)所示。

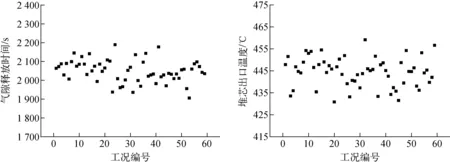
圖5 氣隙釋放時間和堆芯出口溫度Fig.5 Gas release time and CET

ρ=

(2)

式中：RXi為Xi在X中的大小排序；RYi為Yi在Y中的大小排序；ρ為秩相關系數；n為樣本數。

輸入參數與堆芯出口溫度間的Spearman秩相關系數如圖6所示，計算結果表明，氣隙釋放對應的堆芯出口溫度對衰變熱系數和包殼厚度較為敏感。

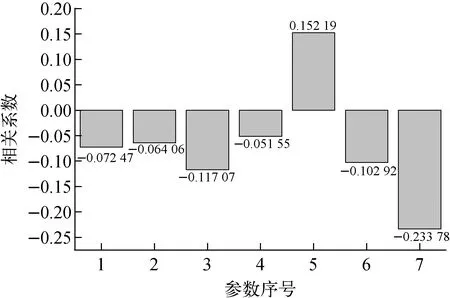
圖6 輸入參數與堆芯出口溫度的 Spearman秩相關系數Fig.6 Spearman rank relational coefficient of input parameter and CET

4 結論

以VVER1000壓水堆核電廠LBLOCA始發嚴重事故為研究對象，MELCOR為研究工具，開展了輸入參數對堆芯出口溫度的不確定性和敏感性研究，得到的結論如下：1) 氣隙釋放時間和堆芯出口溫度單側統計容忍限值(95/95)分別為1 905.71 s和430.85 ℃；2) 氣隙釋放對應的堆芯出口溫度對衰變熱系數和包殼厚度較為敏感。