深部巖體水力劈裂分析及臨界水壓力計算

左擁軍

（萬年縣水利局，江西萬年335500）

0 引言

水力劈裂是指巖體或者其他脆性材料在高水頭作用下，其內部裂紋發生擴展及貫通現象[1]。巖體內部結構因水力劈裂作用而改變，導致滲透性增加，同時，滲透性的增加又會導致滲流速度增加，使得水力劈裂作用進一步增強，如此循環，最終使得整個巖體結構發生破壞。深埋水工隧洞施工時出現涌水、高壓輸水構筑物發生破裂滲漏等均是水力劈裂造成工程事故的典型例子[2]。

水力劈裂最初是應用于石油行業，隨著水利水電工程的迅速發展，越來越多的工程建設中均涉及到水力劈裂問題。崔少英等[3]通過對水工隧洞中水力劈裂臨界孔隙水壓力進行了研究，并得出了3 種類型裂縫和無裂縫情況下的臨界孔隙水壓力計算方法。黃潤秋等[4]對圍巖發生水力劈裂時，隧道出現涌水現象進行了研究，認為當裂紋面受到法向壓應力時，其裂紋的擴展多表現為Ⅱ裂紋問題，并給出了臨界水壓力的計算判據。本文針對深部巖體出現的水力劈裂現象進行分析，利用斷裂力學理論，在拉剪、壓剪復合型破壞模式下，深部巖體原裂紋方位角和側壓力系數對臨界水壓力的影響規律進行深入研究。

1 巖石斷裂破壞模式

關于陶瓷、金屬等材料的裂紋擴展問題，最早是采用經典斷裂力學進行研究的。裂紋附近遠場應力主要是拉力和剪力，而自然界中巖體內裂紋在構造應力和地應力作用下多處于受壓狀態，加上巖體自身結構構造的特殊性，大量文獻表明，巖石類材料與金屬材料之間的斷裂力學行為有很大差別。若當巖體處于地下深部時，此時還會受到孔隙水壓力的作用，其斷裂破壞模式更為復雜。因此，遠場地應力、垂直和水平地應力的相對值及孔隙水壓力是影響深部巖體內裂紋失穩擴展的主要因素。由此可知，要進行深部巖體臨界水壓力的計算，必須先判別其破壞模式。

1.1 力學模型的建立

巖體內裂紋的分布是不均勻的，為方便計算，本文建立了含閉合單裂紋巖體的計算模型，如圖1所示，其目的是研究孔隙水壓力對深部巖體斷裂模式的影響及臨界水壓計算。圖中σ1和σ3為閉合裂紋受到的遠場地應力，α為閉合裂紋與垂直方向上的地應力σ1之間的夾角（裂紋方位角），閉合裂紋內作用有孔隙水壓力p。假設孔隙水壓力沿裂紋各個方向的作用力是相同的，巖體為脆彈性，則根據應力狀態分析可知，此時裂紋面上的正應力σα和剪應力τα分別為：

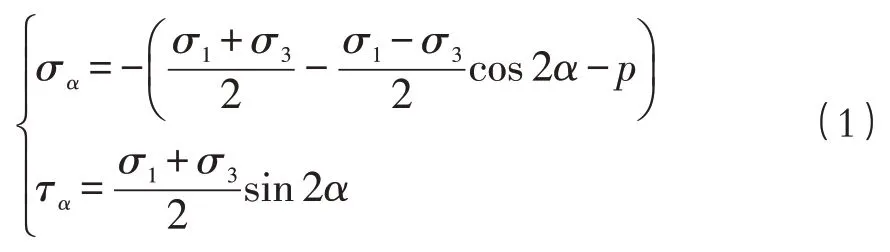
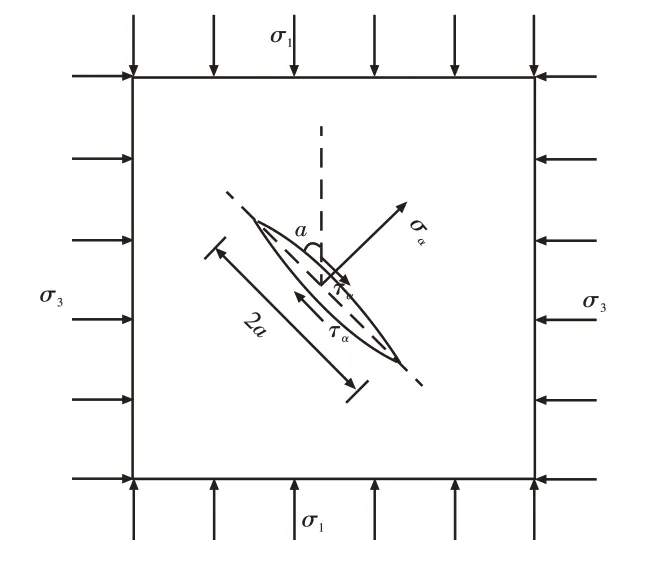
圖1 含單裂紋巖體計算模型

1.2 裂紋失穩擴展模式

由于裂縫面上的應力在斷裂力學中規定受拉為正、受壓為負，而巖石力學中的規定與之相反，所以需在式（1）前面加上負號。由式（1）可知，裂縫面上既存在正應力又存在剪應力，因此，裂紋失穩擴展問題應屬于Ⅰ-Ⅱ復合型裂紋問題。此時裂縫面上的正應力σα有兩種情況。

1）當裂縫面上的正應力σα為拉應力時，裂紋的失穩擴展問題應屬于拉剪復合型問題。目前，對于拉剪復合型裂紋斷裂準則，有最大周向應力理論、應變能密度因子理論及能量釋放率理論，這些準則由于在計算中比較繁瑣，使得工作量較大，且不易得到臨界水壓力的計算顯示。基于此，本文采用近似斷裂準則，得到拉剪復合型裂紋失穩準則：

式中：KⅠc為Ⅰ型斷裂韌度；KⅠ為Ⅰ型應力強度因子；KⅡ為Ⅱ型應力強度因子。

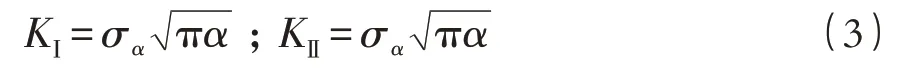
式中：α為閉合裂縫半長。

2）當裂縫面上的正應力σα為壓應力時，裂紋的失穩擴展問題應屬于壓剪復合型問題。關于巖體的壓剪斷裂機制，大量研究表明[3，4]，巖體內的裂紋在壓剪復合應力狀態下，裂紋會逐漸閉合直至壓緊，隨后裂縫面間會發生相對滑動，受巖體的節理構造及組成晶格等因素影響，裂縫面在發生滑動時其裂紋尖端會出現明顯的剪脹現象，而圍壓又會抑制這種現象。因此，巖體在壓剪復合應力狀態下的斷裂機理十分復雜，導致關于壓剪斷裂破壞機理還未形成一套完整的、被工程所認可的準則。基于此，本文就文獻［5］提出的經驗準則對巖體的壓剪特性進行研究，計算公式如下：

式中：λ為壓剪參數，可由試驗獲取；為處于壓縮狀態下巖體的Ⅱ斷裂韌度。式（4）中，當KⅡ為0 時，則為Ⅰ型斷裂，即：

由式（5）可知，λ反應了處于壓縮狀態下的巖體材料Ⅱ斷裂韌度與其Ⅰ斷裂韌度的比值。

2 巖體裂紋失穩臨界水壓力計算

2.1 拉剪狀態下的臨界水壓力

假設巖體內裂紋失穩擴展時的孔隙水壓力為臨界水壓力，將式（1）代入式（3），再代入式（2）即可得到巖體在拉剪狀態時的臨界水壓力，計算公式如下：

式（7）中m為側壓力系數，反映了裂紋周圍圍壓的大小，而圍壓關系著巖體內裂紋失穩擴展方向。因此，分析側壓力系數對臨界水壓力的影響是有必要的。

根據式（7），可得到在不同側壓力系數下的廣義臨界水壓力與裂紋方位角的關系，如圖2 所示。由圖2 可知，隨著側壓力系數的增加，廣義臨界水壓力也在逐漸增加。當m＜1.0和α=0°時，廣義臨界水壓力取得最小值，由此可知，當原裂紋處于垂直方向時，易發生水力劈裂現象；當m=1 時，廣義臨界水壓力為一定值，與原裂紋方位角無關，此時裂紋各個方向的受力狀況相同；當m＞1.0和α=0°時，廣義臨界水壓力取得最小值，即當原裂紋在水平方向時，易發生水力劈裂現象。

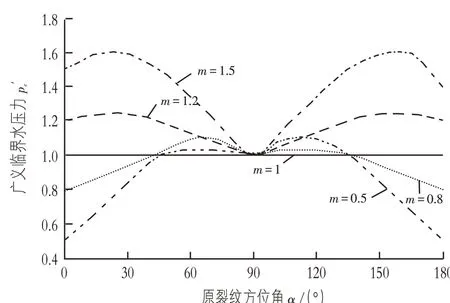
圖2 拉剪狀態下廣義臨界水壓力與原裂紋方位角的關系

2.2 壓剪狀態下的臨界水壓力

據上文分析可知，壓剪狀態下，裂縫面最終會發生相對滑動現象，此時裂縫面間的有效剪應力τe是導致裂紋失穩的主要因素，其計算公式為：

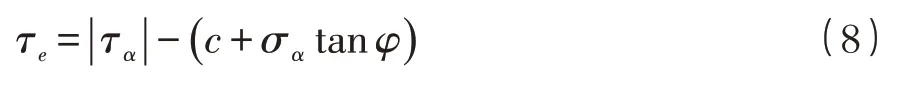
式中：φ為裂縫面間的內摩擦角；c為裂縫面間的粘聚力。

根據公式（4）得到壓剪狀態下裂紋失穩擴展時的廣義臨界水壓力：

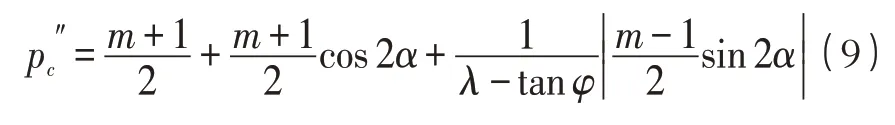
式中：所表示的含義同拉剪狀態下的一樣，但其具體表達式不同，即：

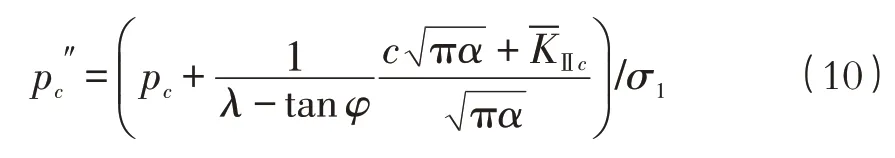
其中需注意：1）公式（4）需在壓應力為正的條件下方可得到，所以式（8）～（10）中，σα也需在壓應力時取正；2）由于莫爾-庫侖準則表示的是極限狀態時的關系，式（8）中的有效剪應力需大于0 才能使式（9）成立；3）在計算中得到的臨界水壓力還需滿足式（1）小于0，否則表示在該條件下裂紋失穩擴展時不會發生壓剪復合斷裂。

不同側壓力系數下的廣義臨界水壓力與裂紋方位角的關系，如圖3 所示。由于式（9）中（λ-tanφ）的正負號未確定，得到的廣義臨界水壓力會有差異。因此，在計算過程中引入文獻［7］的數據：1）當（λ-tanφ）＜0 時，取λ=0.3，tanφ=0.365；2）當（λ-tanφ）＞0 時，取λ=0.7，tanφ=0.365。由圖3（a）可知，當（λ-tanφ）＜0 時，所有曲線（m= 1 時除外）均在45°和135°時取得極小值。側壓力系數越接近1，廣義臨界水壓力越大，并在m= 1 時取最大值；當（λ-tanφ）＞0 時，其廣義臨界水壓力的分布規律基本同拉剪復合斷裂模式下的一致。

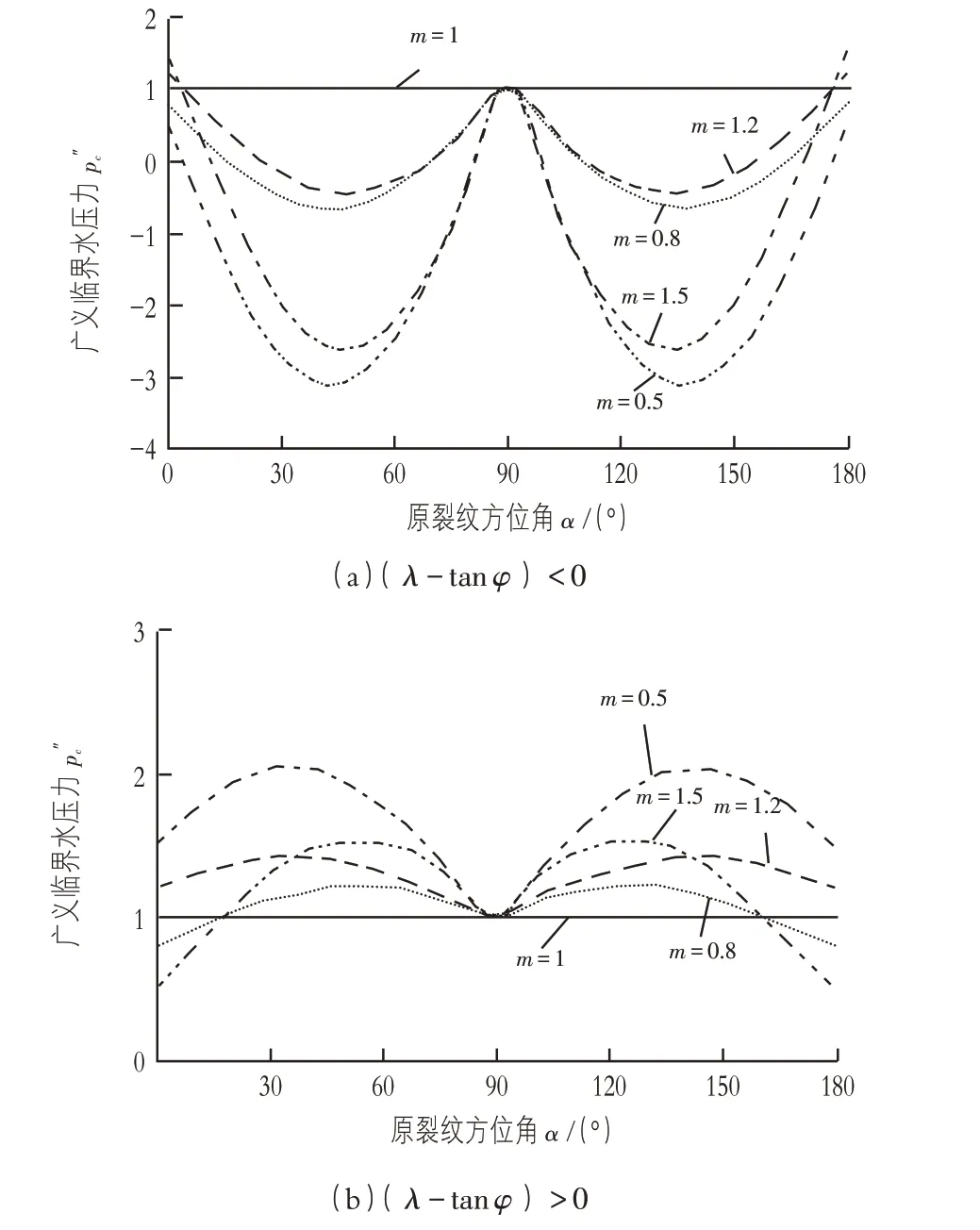
圖3 壓剪狀態下廣義臨界水壓力與原裂紋方位角的關系

3 結語

由于深部巖體內裂紋會受到孔隙水壓力的作用，其失穩擴展時會發生拉剪復合斷裂或壓剪復合斷裂。因此，對于不同情況下的破壞模式，需進行分別討論。上文針對深部巖體，對其內部裂紋失穩擴展的破壞模式進行的研究，得出以下結論：

1）深部巖體內裂紋的擴展無論是壓剪復合型還是拉剪復合型，只要當側壓力系數為1 時，其臨界水壓力均不會因原裂紋方位角的改變而改變。

2）當裂紋的擴展屬于拉剪復合斷裂問題時，臨界水壓力會隨著側壓力系數的增加而增加。當側壓力系數m＜1.0 和原裂紋方位角α=0°時，原裂紋在垂直方向最容易發生水力劈裂現象；當側壓力系數m＞1.0 和原裂紋方位角α=90°時，原裂紋在水平方向最容易發生水力劈裂現象。

3）當裂紋擴展屬于壓剪復合斷裂問題時，臨界水壓力的分布規律受（λ-tanφ）的正負號的影響。當（λ-tanφ）＞0時，其臨界水壓力的分布規律與拉剪復合斷裂時的基本一致；當（λ-tanφ）＜0時，原裂紋在方位角為45°和135°時，最容易發生水力劈裂現象。