定形相變蓄熱單元周期性釋熱實驗分析

李 偉 劉向農 楊 磊 仰 葉 牛玉龍 吳 濤

(1 合肥工業大學汽車與交通工程學院 合肥 230009；2 中國電子科技集團公司第十六研究所 合肥 230088)

隨著熱存儲技術在工業余熱、太陽能蓄存、電力儲能等能源領域中的地位日益提高，具有能量密度高、污染性低、使用場合靈活等優勢的相變材料(phase change material，PCM)在儲熱技術中得到廣泛的應用。相變材料利用加熱時的物態變化，使用潛熱吸收大量熱能，之后在需求端釋放熱量，實現熱能的有效使用。然而，相變材料尤其是有機相變材料的導熱系數低，同時，材料固-液相變時液態具有流動性，這大大制約了相變蓄熱技術的發展。因此蓄熱材料的傳熱強化以及綜合應用場景的開發都是亟需解決的問題。

傳熱強化方面，A.Karaipekli等[1]使用膨脹石墨和硬脂酸混合制備了定形相變復合材料，它是將高分子材料與有機相變材料混合，使高分子材料形成網格結構包裹有機相變材料，有效遏制了相變流動，提高了導熱系數。J.Gasia等[2]使用正十八烷為相變材料，在傳熱管外使用翅片及管間填充金屬棉，提高了蓄熱器蓄放熱性能。張靖馳等[3]將正十八烷分別填充到泡沫銅和泡沫碳中，對比得出正十八烷與泡沫碳復合更有利于提升其傳熱能力及溫控性能。程友良等[4]通過模擬不同導熱系數的傳熱流體，得到了導熱系數對放熱速率的影響規律。郭紹振等[5]使用硬脂酸和癸酸制作梯級組合蓄熱裝置，驗證得出相變復合材料進行梯級組合時蓄熱裝置的最佳蓄熱工況。更多的研究從材料性能與蓄熱結構方面強化傳熱，而缺少從釋熱方式上研究蓄熱裝置的傳熱性能。

相變材料的綜合應用方面，T.Laclair等[6-8]開發了PCM與PTC加熱器共同作用的電動汽車加熱系統，改善了低溫環境運行下的車室內供熱問題。Qi Lingfei等[9]提出一種基于相變材料的車用太陽能風冷系統，有效解決了夏季車室內溫度過高的問題。R.Anish等[10]研究了赤藻糖醇殼管式多翅片蓄熱單元不同運行工況對其蓄放熱特性的影響。Ling Ziye等[11]用PCM復合材料包裹電動汽車鋰電池，提高了它在低溫工況下的放電性能。研究人員開發新的相變材料使用場景，但忽略了相變材料在實際應用時蓄放熱是間歇性的。

因此，考慮到相變蓄熱的實際應用中，釋熱是非連續的，而目前對于周期性釋熱性能的研究還較少。本文采用響應面分析的實驗設計方法，在一定范圍內改變相變蓄熱單元運行時間，對蓄熱材料釋熱量、釋熱動力、釋熱火用效率進行分析，得到最佳的運行時間。

1 實驗設計及方法

1.1 實驗材料與裝置

實驗所用復合相變材料是由純赤藻糖醇粉末添加質量分數為3.5%的膨脹石墨混合，經由模具壓實為黑色環狀固體。在293～413 K的溫度區間內加熱，吸附在膨脹石墨孔隙內的赤藻糖醇會發生相態變化，但由于膨脹石墨的包裹，宏觀上表現為固-固相變。使用DSC、激光導熱儀測試其熱物性，如表1所示。

表1 赤藻糖醇復合相變材料熱物性

相變材料制作完成后，需要搭建相變蓄熱單元模塊。如圖1所示，相變蓄熱單元從外到內依次為絕熱層、電加熱膜、相變材料、傳熱管。絕熱層使用氣凝膠保溫棉，平均導熱系數約為0.02 W/(m·K)。電加熱膜包圍于相變材料外，使用扎帶固定。傳熱管采用光滑銅管。本實驗中，傳熱管外半徑R1=4 mm，相變環外半徑R2=40 mm，模塊整體半徑R3=80 mm，蓄熱單元的長度為350 mm。

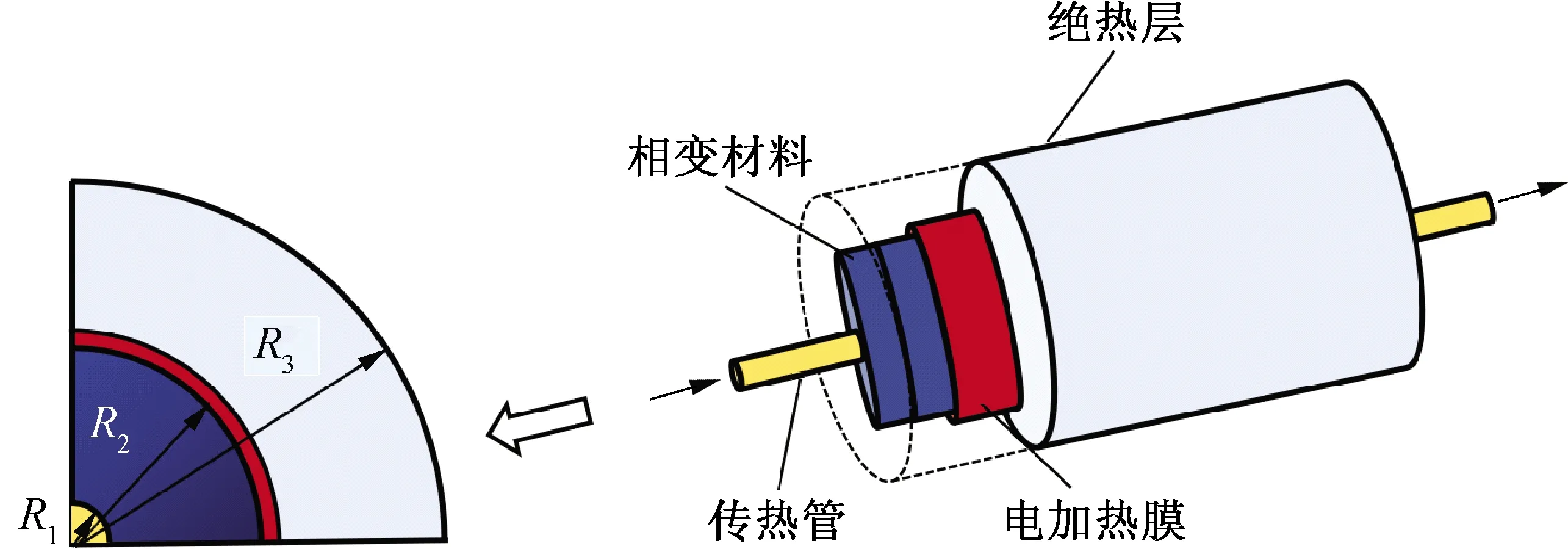
圖1 相變蓄熱單元模型

對相變蓄熱材料進行加熱與釋熱的實驗系統如圖2所示，恒溫水箱和中轉水箱設定為303 K，恒溫水箱在釋熱時，提供穩定恒溫流體，中轉水箱為實驗系統提供工作流體的補給同時平衡管路壓力。兩個水泵分別從恒溫水箱和中轉水箱中抽出工作流體，水泵1為可調速水泵。流量計用來監測相變蓄熱單元入口流量。相變蓄熱單元加熱部分由電加熱膜、示功儀和調壓器組成，后兩者主要負責監測和控制加熱數據，實驗采用85 W穩定功率對材料外壁進行加熱。根據加熱測試，當材料溫度達到相變溫度區間上限以上5 K，此時蓄熱完成，開始釋熱實驗。當系統運行時，打開所有水閥和水泵，而系統間歇時，需要依次關閉水閥1、水閥2、水閥3、水泵，將相變蓄熱單元內傳熱流體排出，累計釋熱時間達到40 min時，停止實驗。

圖2 周期性釋熱實驗系統

為了對相變蓄熱單元周期性釋熱性能進行分析，實驗系統中的數據采集模塊負責采集壁面平均溫度和傳熱管進出口溫度。相變材料外壁溫度由均勻放置的4個熱電阻獲取，進出口傳熱流體溫度由管口放置的熱電阻獲取。具體的熱電阻安裝圖如圖3所示。

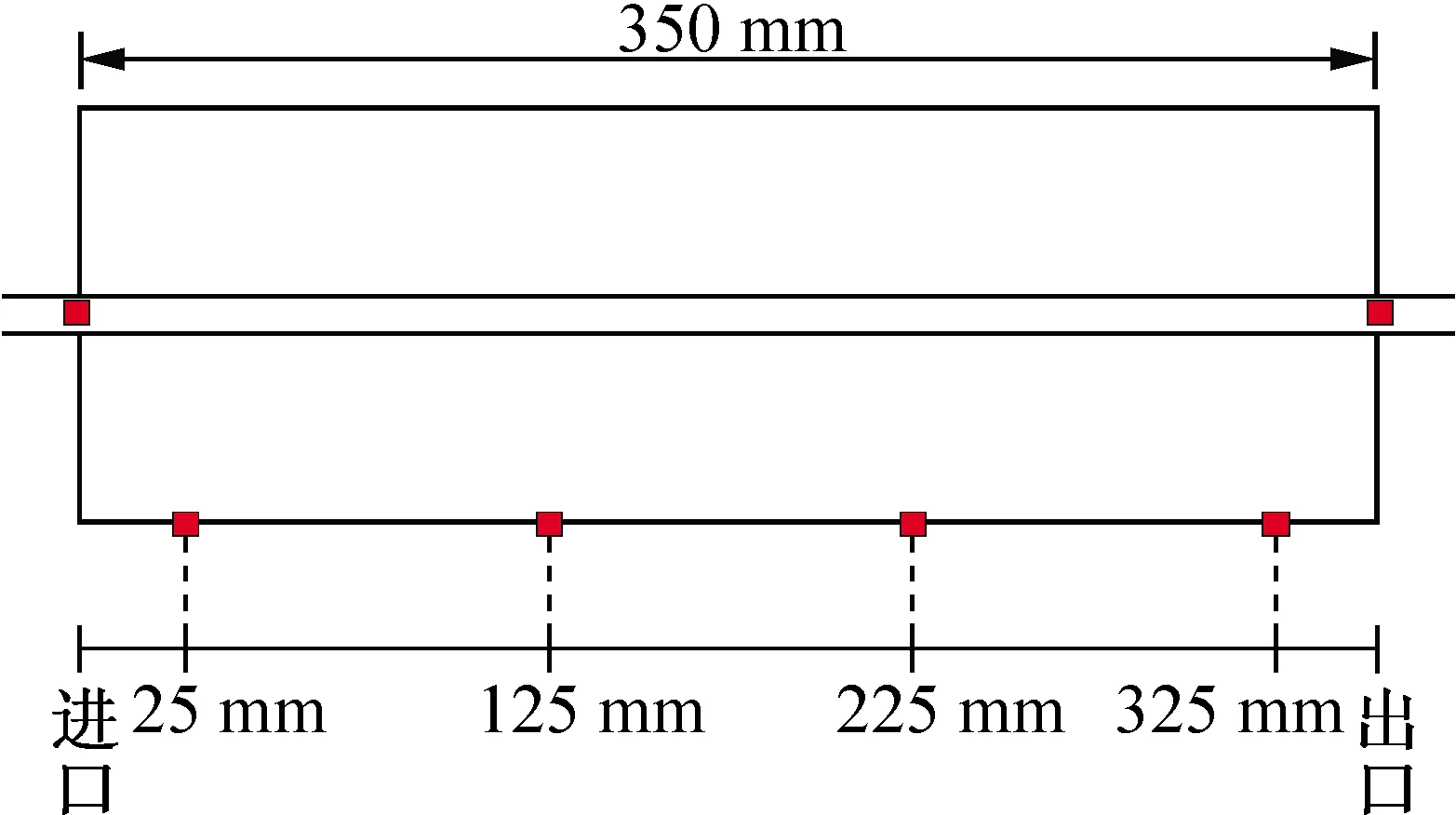
圖3 相變蓄熱單元熱電阻分布

1.2 實驗評價指標

實驗采用定形相變材料的總釋熱功率、無量綱材料溫度-斯蒂芬數以及釋熱火用效率作為評價指標。這3個評價指標數值均可由采集的原始溫度數據推導得到。

首先，當忽略傳熱熱阻損失時，單位時間內傳熱流體通過傳熱管從相變材料中獲取的熱量等同于蓄熱材料的逐時釋熱功率，而總釋熱功率是由逐時釋熱功率求和而成，反映了總釋熱量的大小，計算式如式(1)所示。

(1)

式中：Qi為單個溫度采集周期內，傳熱流體吸收的熱量，kJ，通過熱量計算式可以求得；Δx為數據采集儀設置的采集周期，Δx=2 s。

其次，由于復合相變材料和傳熱流體之間的溫差越大，它們之間的傳熱動力越大，由于傳熱流體的溫度變化相對于相變材料溫度而言較小，所以本文使用相變材料外壁平均溫度反映釋熱動力的大小。為了使研究更具普遍性，引入斯蒂芬數(Stm)，它包含了潛熱和顯熱兩方面，如式(2)所示。

(2)

式中：cp為相變材料比熱，kJ/(kg·K)；Tw為累計釋熱40 min時相變材料外壁平均溫度，K；Tm為相變材料平均相變溫度，K；L為相變潛熱，kJ/kg。此外，Stm越小表明相變材料溫度越高，說明與傳熱流體的溫差越高，即釋熱動力越大。

最后，為了對周期性釋熱系統的回收能量品質進行完備的的分析與評價，針對其在不同運行時間下的釋熱火用進行分析，對比不同運行時間的釋熱完成時火用效率大小。

在此，忽略泵功和傳熱流體的壓力損失，相變蓄熱單元的釋熱火用效率ε定義如下[12]：

(3)

其中，

(4)

(5)

式中：t為釋熱總時間，s；Tin和Tout分別為傳熱管進出口溫度，K；T為傳熱流體溫度，K；qm為傳熱流體質量流量，kg/s；cf為流體比熱容，kJ/(kg·K)；式(5)中，等式右側第一項表示相變材料固態顯熱火用，第二項表示其潛熱火用，第三項表示液態顯熱火用，其中，cp,s和cp,l分別為相變材料固態和液態比熱容，kJ/(kg·K)；mpcm為相變材料的質量，kg；Tini為材料初始溫度，K；Tpcm為材料加熱完成時的平均溫度，K；T0為環境溫度，K。

1.3 響應面實驗設計

響應面分析法是使用響應面等值線的分析尋求最優工藝參數，通過回歸擬合因素與響應值之間函數關系的一種統計方法。包括實驗設計、建模、檢驗模型的適應性、尋求最佳的組合條件等眾多實驗和統計技術[13]。對過程數學建模和回歸擬合后，可以求出對應因素的響應值。

采用實驗設計軟件Design Expert中RSM(response surface methods)中的單因子設計模塊。實驗條件是間歇時間固定為20 min，運行時間變化范圍為2.5～12.5 min。同時，實驗采用累計釋熱時間為40 min時，定形相變材料的總釋熱功率、無量綱材料溫度-斯蒂芬數以及釋熱火用效率為響應參數。

根據原始溫度數據計算響應參數的數值，并在Design Expert中設置實驗條件和響應值，得出實驗設計方案，如表2所示。

表2 響應面實驗設計與結果

2 結果與分析

2.1 釋熱量分析

當相變材料釋熱時，采用恒定進口溫度為30 ℃，恒定流量為1 L/min的傳熱流體從相變蓄熱單元中吸收熱量，其逐時釋熱功率和進出口溫差均可反映相變材料的釋熱量。在此，先使用響應面分析的方法，研究不同運行時間對于其總釋熱功率的影響。

使用最小二乘法，利用表2中的數據擬合響應曲線，得到運行時間to(min)與總釋熱功率P(kW)的函數關系：

P=166.136 +13.857to-9.731×10-3to2-

0.684to3

(6)

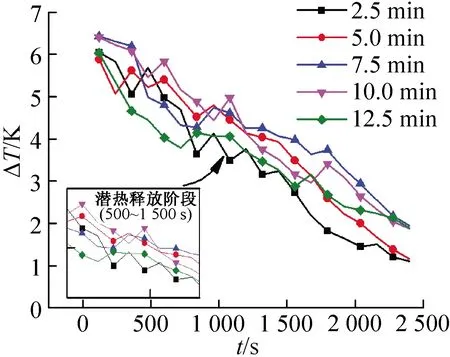
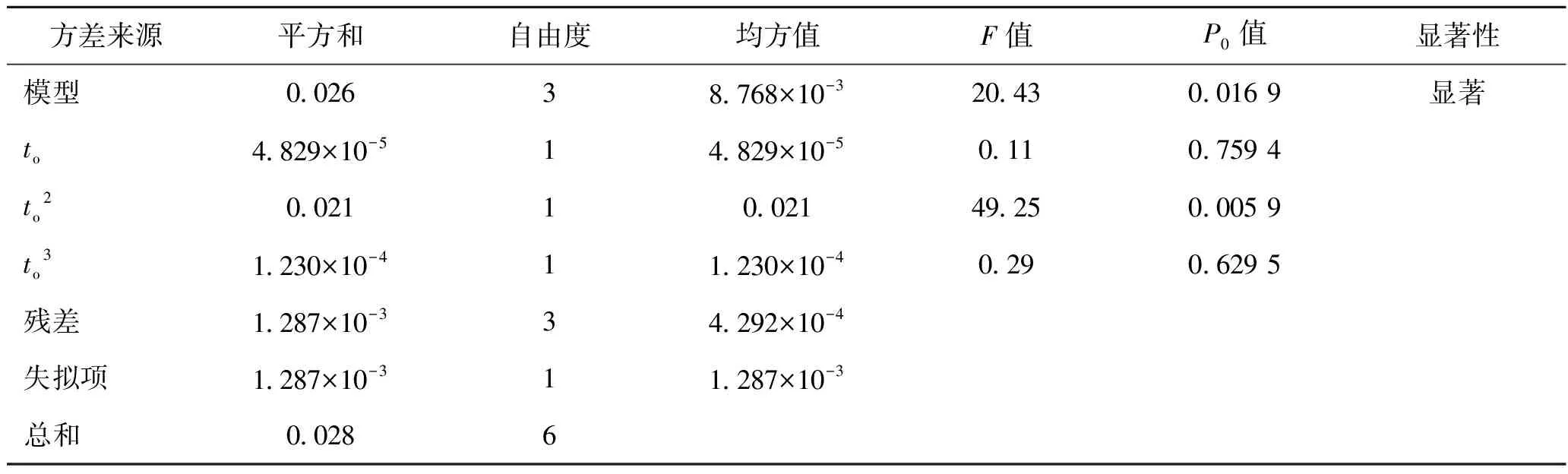
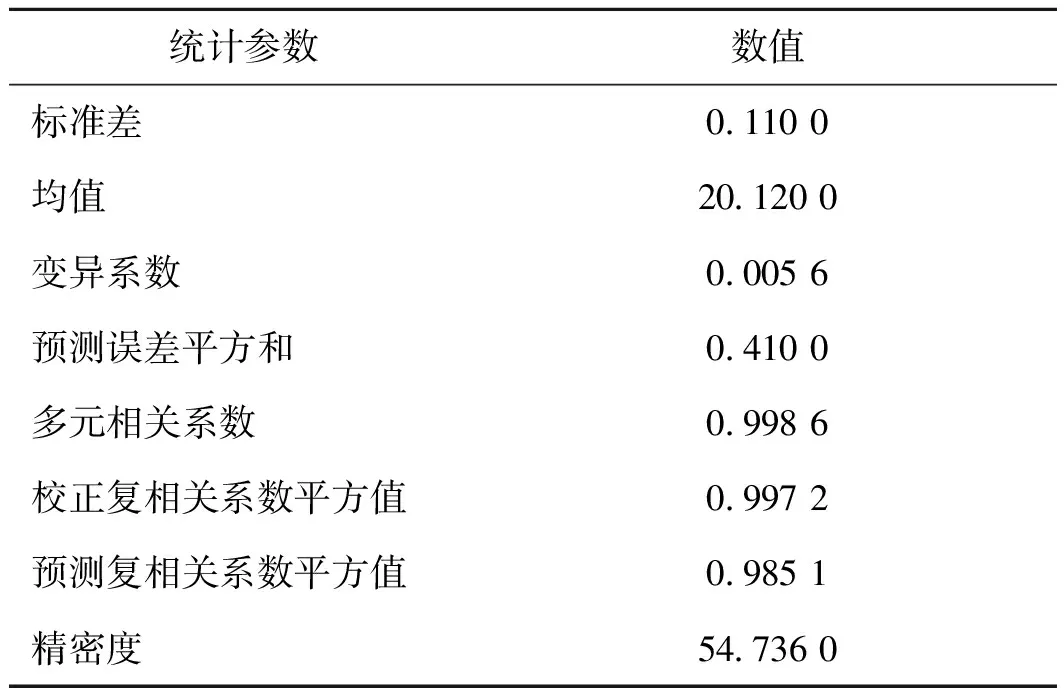
通過方差分析和誤差統計分析評價建立的響應曲線模型的適應度。表3所示為釋熱總功率的方差分析結果。表中的統計特征量F表示模型引起的均方與殘差均方的比值。若F超過某一臨界值Fα,k,n-k-1時，則拒絕原假設H0。而P0值為特征量F

表3 釋熱總功率方差分析結果

釋熱總功率的擬合回歸方程誤差統計分析如表4所示。表中多元相關系數表征數據相關性，值越大說明相關性越好；校正復相關系數平方值和預測復相關系數平方值高且接近，一般認為兩者之差小于0.2，則表示對響應參數的解釋是充分的；變異系數小于0.1即可表明實驗的可信度和精確度高；精密度是有效信號與噪聲的比值，若大于4視為合理[15]。由表4可知，該模型的擬合回歸方程的相關統計參數符合校核標準，具有很好的適應性。

表4 釋熱總功率回歸方程誤差統計分析

根據式(1)的函數關系，作運行時間對總釋熱功率P的響應曲線，如圖4所示，可以看出隨著運行時間的增加，總釋熱功率P呈現先上升后下降的趨勢。由于累計釋熱時間相同，總釋熱功率越大，則總釋熱量越大，相變蓄熱材料的平均釋熱速率也就越快。原因是圓環形相變蓄熱單元在釋熱時，靠近傳熱管的相變材料由于先發生熱量傳遞，所以溫度較低，遠離傳熱管的一側，后發生熱量傳遞，溫度較高，在同一時刻，材料內部存在溫差。系統間歇時，相變材料自均衡內部溫差，靠近傳熱管處相變材料溫度提高，當系統再運行時，釋熱功率也會相對提高，這是曲線后半段下降的原因。

同時考慮到材料溫度越高，與環境溫差越大，熱耗散越多。此時，由于間歇時間均為20 min，為了保持總釋熱時間相同，運行時間越短，則間歇次數越多，這加劇了相變蓄熱單元在環境溫度下的熱損失。所以運行時間較短時，總釋熱功率反而較小。因此，蓄熱單元在間歇時的溫度自均衡程度和它在環境溫度下的熱損失大小是影響釋熱功率的關鍵因素。由圖4可知，運行時間約為8.5 min，釋熱功率達到峰值，此時溫度均衡程度與熱損失達到了相對優化的平衡。

圖4 運行時間對總釋熱功率響應曲線

為了全面分析釋熱量，還應研究不同運行時間的進出口溫差ΔT隨著釋熱時間t的變化規律，為了便于對比，將間歇時間段溫度數據剔除。相同間歇時間不同運行時間進出口溫差變化如圖5所示。由圖5可知，在釋熱開始階段，進出口溫差維持相對較高的水平，且下降速度較快，這是因為相變材料初始溫度高，且前期是將存儲的液態顯熱傳遞給溫度較低的傳熱流體。隨著液態顯熱的逐步釋放，相變材料進入潛熱釋放階段，由于潛熱存儲熱量占據總熱量的60%以上[16]，此時，傳熱流體吸收相變材料潛熱，進出口溫差下降趨勢變得相對緩和。同時從圖中可以得出，由于周期性釋熱，有機相變材料釋熱時固有的過冷現象得到了很大的改善。最后，溫差下降速度增大，因為相變材料又進入固態顯熱釋放階段。

圖5 相同間歇時間不同運行時間進出口溫差變化

對比不同運行時間的ΔT可以發現，在潛熱釋放階段，運行時間為5.0、7.0、10.0 min組，溫差較高。2.5 min組前期溫差高，中后期均為最低的，原因在于2.5 min組有著更多的間歇時間，因此，隨著釋熱時間增加，熱損失也在增加。12.5 min組一直維持相對較低的溫差。在顯熱釋放階段，7.5 min組溫差一直處于最高，2.5 min組溫差最低，其他3組互有交替。溫差交替的原因在于，材料溫度相對較低，各組熱損差異較小，但由于運行時間不同，雖處于同一釋熱時間，卻在不同的釋熱階段。考慮到實際應用，熱損失不可避免，因此考慮整體的溫差，可見7.5 min組的整體進出口溫差相對最高。綜合考慮總釋熱功率和進出口溫差，相對優化的運行時間出現在約8.0 min。

2.2 釋熱動力分析

釋熱動力使用無量綱材料溫度-斯蒂芬數的數值反映其大小。先使用最小二乘法，利用表2中數據擬合響應曲線，得到運行時間to與斯蒂芬數Stm的函數關系：

Stm=0.778-0.111to+9.232×10-3to2-1.775×

10-4to3

(7)

采用與2.1節中相同的方法，得到如式(7)所示的關于斯蒂芬數的擬合回歸曲線。其方差分析與誤差統計分析的結果如表5和表6所示。可以得到，各項參數的值均符合相關的檢驗原則，說明關于斯蒂芬數的模型是可靠的。

表5 斯蒂芬數方差分析結果

表6 斯蒂芬數回歸方程誤差統計分析

根據式(7)繪制運行時間對斯蒂芬數Stm的響應曲線，如圖6所示，隨著運行時間的增加，斯蒂芬數先減少后增加，即相變材料的釋熱動力先增大后減小。當蓄熱系統運行時，圓環形相變蓄熱材料近傳熱管側熱量釋放快，其傳熱方式主要包括相變材料的導熱與傳熱流體的對流換熱，而遠離傳熱管側主要通過熱傳導向內側傳遞熱量。這直接導致了系統運行時，相變材料內外側溫差維持在高位，且運行時間越長，本身所具有的釋熱動力越小。當系統間歇時，材料內部徑向與軸向發生導熱，使得內部溫差變小，整體釋熱動力上升。所以曲線后半段釋熱動力隨運行時間降低，是因為此時熱損失都相對較少，但累積間歇時間越來越少。而前半段釋熱動力增加是因為運行周期較小時，間歇次數多，熱損失較大，隨著運行周期的增加，熱損減少，釋熱動力表現為上升趨勢。經綜合考量，針對釋熱動力，最優的運行時間出現在7.5 min附近。

圖6 運行時間對斯蒂芬數響應曲線

2.3 火用效率分析

在相變蓄熱系統中，傳遞給傳熱流體的熱量即是回收的有用能，它的利用效率由火用效率表示。使用最小二乘法，利用表2中數據擬合響應曲線，得到運行時間to與釋熱火用效率ε的函數關系：

ε=17.604-0.342to+0.302to2-0.021to3

(8)

重復前兩節的方法，獲得火用效率擬合回歸方程，如式(8)所示。其方差分析結果和誤差統計分析結果分別如表7、表8所示。由表可以得出，擬合回歸方程結果可以通過相關檢驗，適應性很好。

表7 釋熱火用效率方差分析結果

表8 釋熱火用效率回歸方程誤差統計分析

根據式(8)得出釋熱火用效率ε的響應曲線，如圖7所示。由圖7可知，隨著運行時間在給定范圍內增加，火用效率先增加后減少。首先，相變蓄熱單元在加熱時所蓄存的火用分別轉換成傳熱流體蓄存火用、相變材料換熱火用損、材料相變火用損以及環境火用損。其次，相變材料與傳熱流體的溫差越大，火用損越少[17]，說明在潛熱釋放階段，傳熱流體所積累的火用是最多的。因此，曲線后半段火用效率減少的原因在于，運行時間在一定范圍內增加，釋放潛熱的時間短，此時各種火用損均隨運行時間的增加而增大，釋熱火用效率就會較低。

當運行時間過小時，系統間歇次數多。其一，造成環境火用損多；其二，由于圓環形蓄熱材料內側先釋放完潛熱，外側后釋放完，在系統間歇時，內側相變材料會經歷再加熱，會發生反復相變，這也造成材料的相變火用損較大。所以，運行時間過小時的火用效率也較低。通過圖7中響應曲線上升速度小于下降速度可知，釋放潛熱時間短造成的火用損是影響較大的。從火用效率來看，最佳的運行時間在9.5 min附近，相對于釋熱功率與斯蒂芬數極值出現的時間滯后約22%。

圖7 運行時間對釋熱火用效率響應曲線

3 結論

本文對赤藻糖醇/膨脹石墨相變蓄熱單元的周期性釋熱特性進行實驗研究與評價分析，得到如下結論：

1)采用響應面法的單因子設計法設計實驗，進行模擬，建立了總釋熱功率、斯蒂芬數、火用效率與運行時間的回歸方程，通過Design Expert軟件對3個評價指標綜合分析后，得到當間歇時間為20 min時，運行時間為7.7 min為最優化的結果。

2)釋熱過程中，隨著運行時間在范圍內增加，總釋熱量、釋熱動力與有用能量回收率均為先增加后降低，存在極值，且火用效率極值出現時間相對于總釋熱功率和斯蒂芬數要滯后22%。這是由于熱耗散和系統間歇時相變蓄熱單元內部熱量自均衡聯合影響的結果。

3)在實際的周期性釋熱應用中，適當增加潛熱釋熱區間運行時間，減少顯熱釋熱區間運行時間，同時提高蓄熱材料的保溫性能，可以有效提高蓄熱系統運行效率。

對于相變蓄熱單元在間歇時間、傳熱流體流量和進口溫度等參數變化時的性能還可以采取本文提供的研究模式進一步探索。

本文受安徽省自然科學基金(JZ2019AKZR0018)項目資助。(The project was supported by the Natural Science Foundation of Anhui Province(No.JZ2019AKZR0018).)