基于發動機吊耳材料非線性的有限元仿真研究

王俊然，曾超，程市，劉倫倫，沈琳清，謝永勝

(1.內燃機可靠性國家重點實驗室，山東 濰坊 261061；2.濰柴動力股份有限公司，山東 濰坊 261061)

0 引言

發動機吊耳是發動機在吊裝及轉運過程中必不可少的部件，當其強度不滿足要求時，發動機在吊裝或轉運過程中，就會發生吊耳變形，甚至斷裂，進而導致發動機從空中墜落，造成嚴重安全事故和重大的經濟損失[1]。現在對吊耳強度的校核主要以現場吊裝驗證為主。這樣既費時費力，還存在一定危險。目前有限元方法較少應用在校核發動機吊耳強度上，且主要集中在船舶[2]、集裝箱以及航天航空[3]等大型設備的吊裝強度分析等應用上。發動機吊耳與大型設備吊耳有所不同，因此需要建立發動機吊耳強度的有限元仿真分析。

通過拉伸試驗獲取發動機吊耳材料的應力應變數據，考慮材料的非線性[4]行為，建立有限元模型對發動機吊耳進行有限元分析，并結合主機廠實際吊裝情況，證實基于非線性材料對發動機吊耳進行有限元仿真方法的準確性。

1 獲取材料屬性

1.1 測試方法

發動機吊耳的常用材料為Q235和Q345，其應力-應變性能如圖1所示[5]。在小應力和應變情況時表現出近似線彈性的性質[6]，材料剛度即彈性模量是一個常數；在高應力和應變情況下，開始具有非線性的行為，稱其為塑性。從彈性到塑性行為的轉變發生在材料應力-應變曲線上的屈服點。金屬在到達屈服點之前屬于彈性階段，只產生彈性變形，在卸載后可以完全恢復。當應力超過了屈服應力，則進入塑性階段，此時產生的既有彈性形變也有塑性形變，卸載后彈性形變可以完全恢復，但塑性形變將永久保持。當應力達到強度極限時，金屬開始出現頸縮現象，并最終達到破壞。

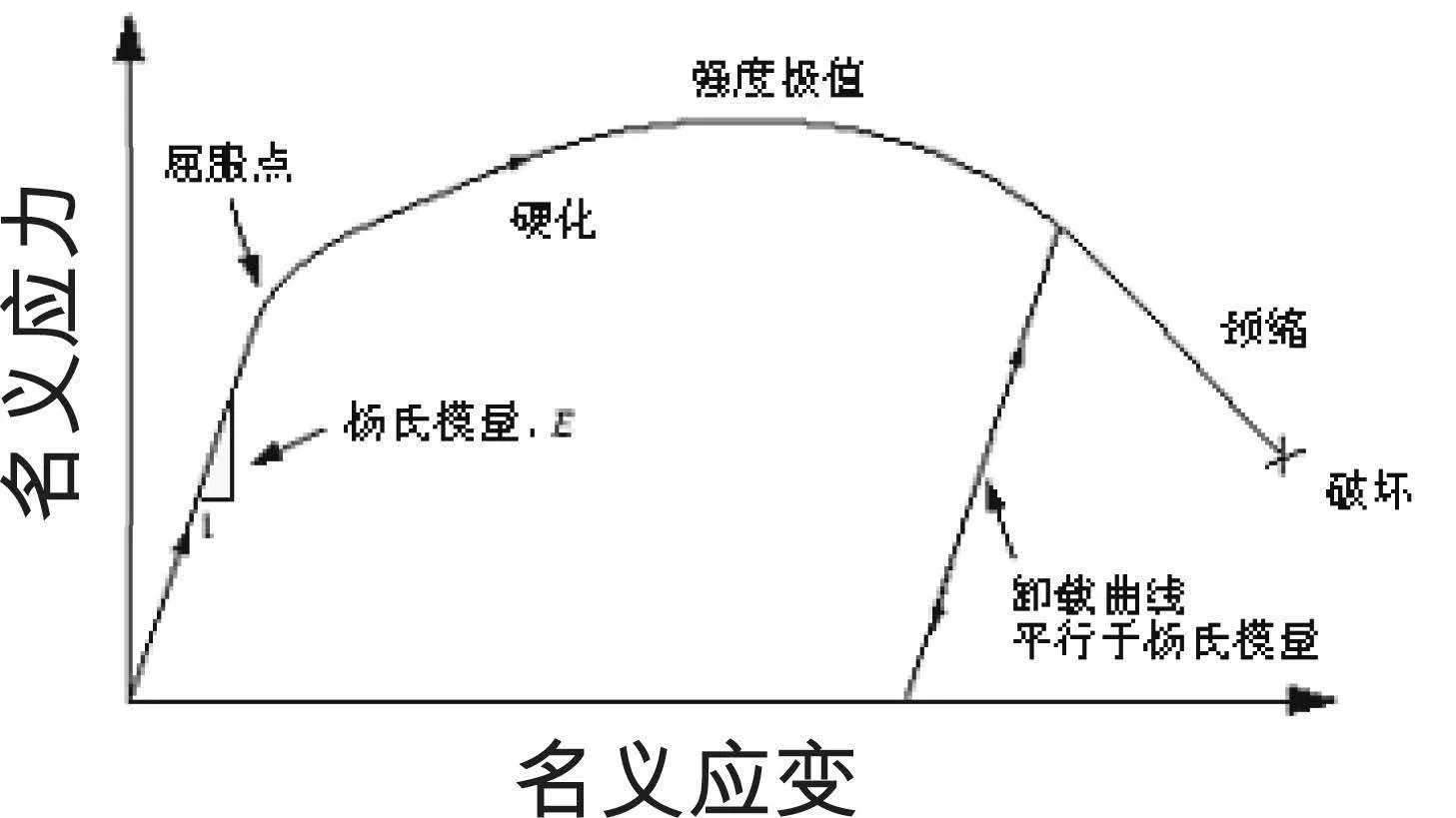
圖1彈塑性材料的應力-應變行為

為獲取發動機吊耳常用的材料屬性，參考國家標準GB/T228.1-2010《金屬材料 拉伸試驗》第1部分：室溫試驗方法。利用深圳萬測試驗設備有限公司的ETM305D-TS拉伸試驗機，對標準的板材拉伸樣件進行拉伸試驗。樣件拉伸試驗前、后如圖2所示。

圖2樣件

1.2 數據處理

通過拉伸試驗，獲取了Q235和Q345的名義應力應變數據，但是在有限元分析中需采用真實應力應變數據，因此要對名義應力應變數據進行轉化，具體公式如下：

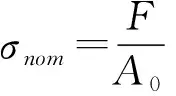
(1)

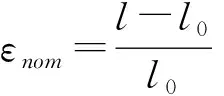
(2)

式中，A0和l0樣件的初始橫截面積和長度；

A和l為某一時刻樣件的橫截面積和長度。由于樣件體積不變，即A0×l0=A×l。

則真實應力：σt=σnom(1+εnom)

(3)

真實應變：εt=ln(1+εnom)

(4)

通過上述公式轉換后得到的材料的真實應力應變和原始的名義應力應變曲線，如圖3、圖4所示。

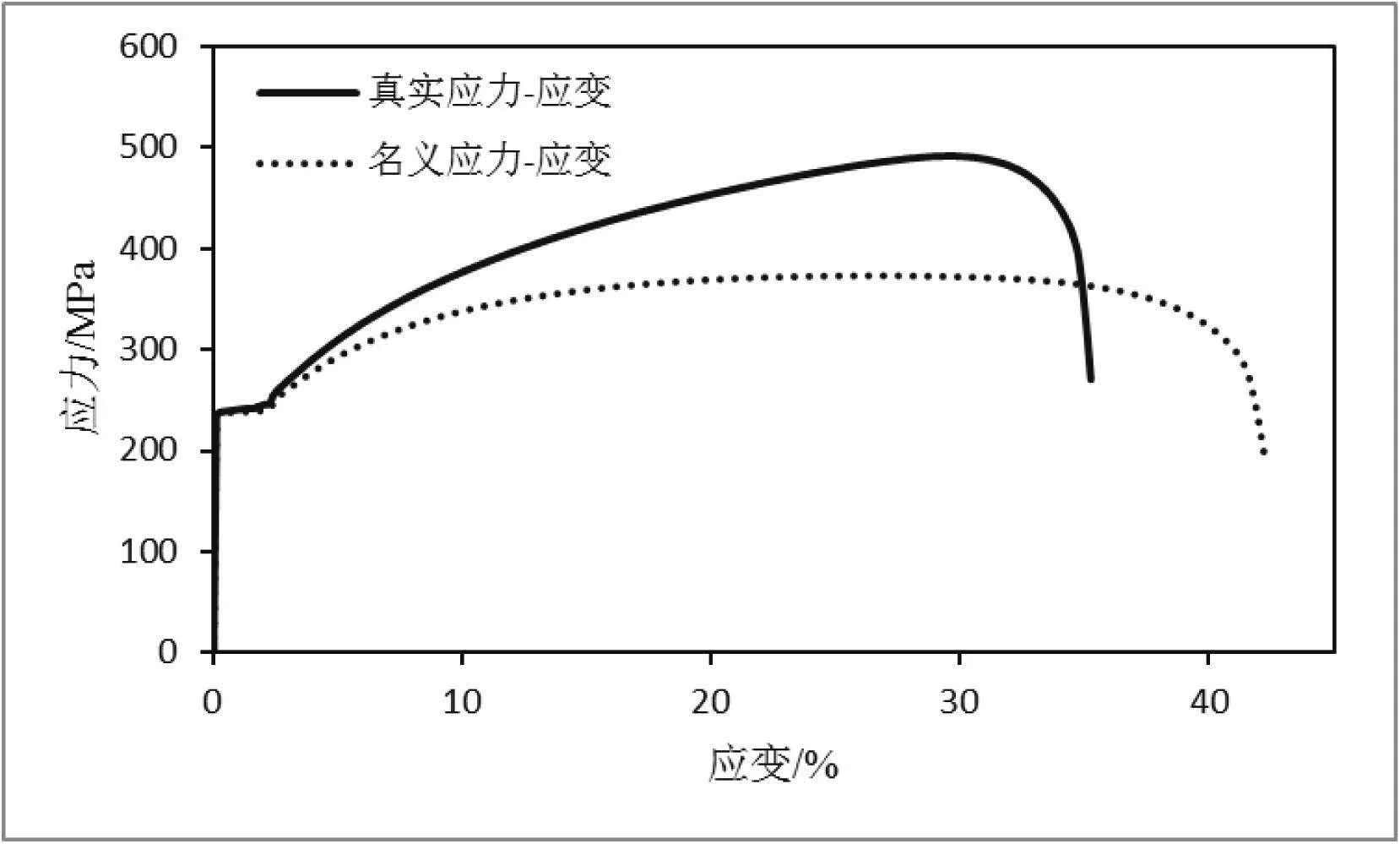
圖3Q235的應力-應變曲線

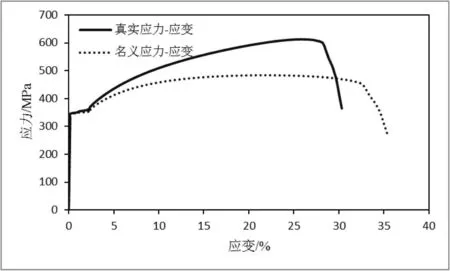
圖4Q345的應力-應變曲線

2 發動機吊耳原結構仿真分析

由于主機廠的條件限制，不能采用垂直起吊，只能采用斜拉起吊，繩索與發動機的水平方向夾角θ=60°，如圖5所示。吊裝過程中后吊耳發生明顯變形，并與消音器發生干涉，結構不滿足要求。

圖5發動機斜拉起吊工況

2.1 發動機吊耳受力分析

發動機斜拉工況受力如圖6a所示，發動機質心不在中心，將導致發動機偏轉。偏轉后的受力如圖6b所示，該工況下吊環受到沿繩索方向的拉力，可將其分解為垂直向上和水平方向的拉力。

起吊過程中，以n倍的發動機重力模擬沖擊載荷，按照兩端吊耳的受力對發動機(動力總成)質心取矩平衡和受力分解關系，得到如下公式：

(5)

(6)

(7)

(8)

上式中：

Gy=G×cosα

(9)

(10)

式中，F1y為前吊耳垂直方向所受的力，F2y為后吊耳垂直方向所受的力，F1x為前吊耳水平方向所受的力，F2x為后吊耳水平方向所受的力，θ為繩索與水平方向的夾角，α為發動機偏轉角度，h為吊耳受力點距質心P的垂直距離，G為發動機重量，L為兩吊環水平距離，a為前吊環距質心P的水平距離，b為后吊環距質心P的水平距離，n為沖擊系數(1-2)。

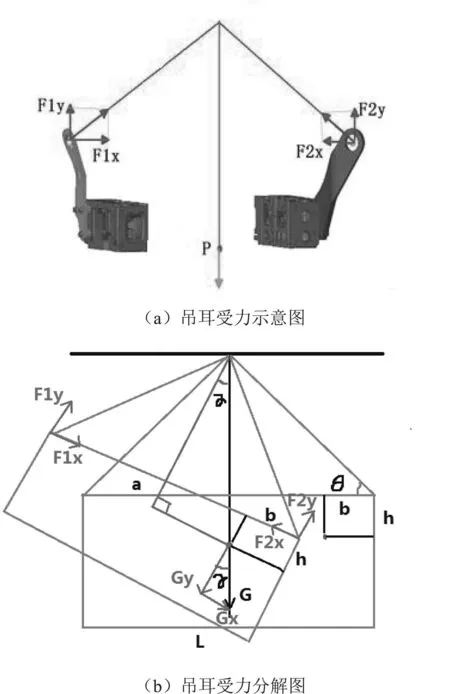
圖6發動機斜拉起吊受力圖

該發動機總成的質量為660 kg，在斜拉工況下，繩索與水平方向的夾角θ=60°，經計算發動機的偏轉角度α=12°，前后吊耳所受的力分別為：F1y=751.5 N；F1x= 43 4N；F2y=8 650 N；F2x=4 994 N。

2.2 彈性材料有限元分析

原結構發動機吊耳的材料為Q235，采用彈性材料進行有限元分析時，材料的彈性模量為212 000 MPa、泊松比為0.288、密度為7 800 kg/m3。發動機吊耳有限元模型，如圖7所示。

圖7發動機吊耳有限元模型

經計算：發動機前吊耳所受最大Mises應力為180 MPa，小于Q235的屈服極限235 MPa，滿足要求；后吊耳所受最大Mises應力為1 400 MPa，遠超屈服極限和強度極限，不滿足要求。但由于僅采用材料的彈性階段屬性，當應力值超過屈服極限后，所產生的應力均為虛假應力，且遠大于吊耳實際所受的應力。因此，當吊耳所受應力超過屈服極限，仍采用彈性階段屬性進行分析，這與實際情況不符，應采用非線性材料屬性進行分析，應力云圖如圖8所示。

圖8彈性材料-原發動機吊耳應力云圖

2.3 非線性材料有限元分析

原結構發動機吊耳采用非線性材料屬性進行有限元分析時，不僅設置材料的彈性階段屬性，還設置材料的塑性階段屬性。經計算發動機前吊耳所受最大Mises應力為180 MPa，小于Q235的屈服極限235 MPa，因為其未超過屈服極限，仍處于彈性階段，所以采用彈性材料和非線性材料計算的結果相同；后吊耳所受最大Mises應力為500.7 MPa，遠小于采用彈性材料的結算結果，但仍大于屈服極限和強度極限，因此力不滿足設計要求，應力云圖如圖9所示。

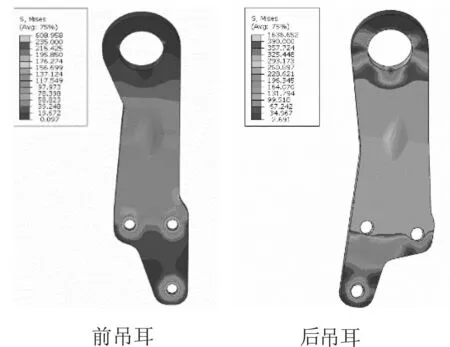
圖9非線性材料-原發動機吊耳應力云圖

通過有限元計算，發動機后吊耳強度不滿足要求，與主機廠反饋的吊裝情況一致，故需要對現有結構進行優化。

3 發動機吊耳優化結構仿真分析

原結構在主機廠吊裝過程出現了變形，為了安全起見對前后吊耳同時進行優化，將原有的向外側折彎結構，優化為直板結構，并對后吊耳進行翻邊處理，來提高其抗彎強度，并將材料由Q235更改為Q345。具體優化數模，如圖10所示。為校核優化后結構是否滿足要求，對其進行有限元分析。

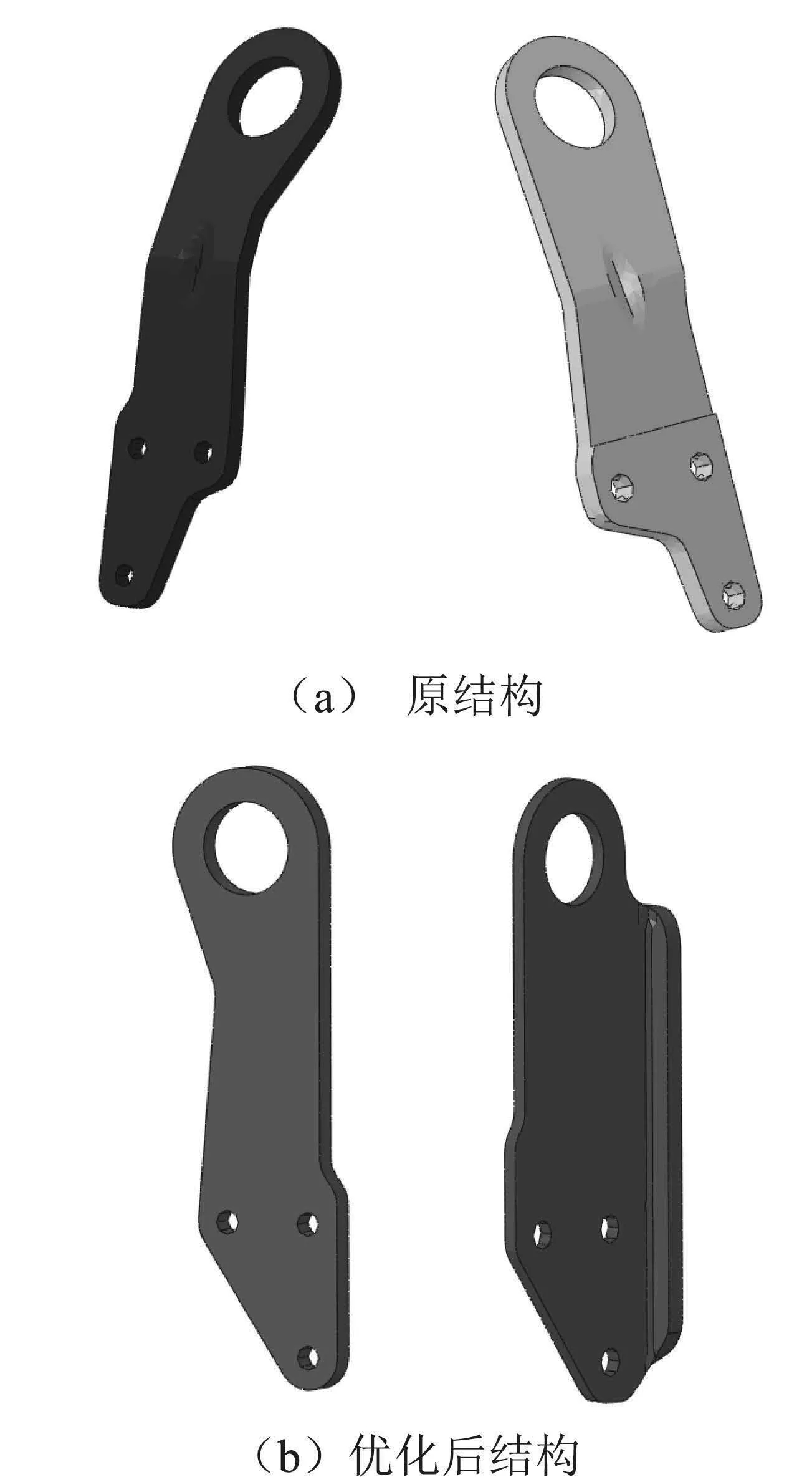
圖10發動機吊耳結構

3.1 彈性材料有限元分析

優化結構發動機吊耳的材料為Q345，采用彈性材料進行有限元分析時，僅設置材料的彈性模量為206 000 MPa，泊松比為0.28和密度為7 850 kg/m2。經計算發動機前吊耳所受最大Mises應力為90 MPa，小于Q345的屈服極限345 MPa，滿足要求；后吊耳所受最大Mises應力為618 MPa，超出屈服極限和強度極限，不滿足要求。應力云圖如圖11所示。

圖11彈性材料-優化后發動機吊耳應力云圖

3.2 非線性材料有限元分析

對優化后的發動機吊耳采用非線性材料屬性進行有限元分析，經計算發動機前吊耳所受最大Mises應力為90 MPa，前吊耳滿足要求；后吊耳所受最大Mises應力為346.5 MPa，超過屈服極限345 MPa，但遠小于強度極限470 MPa。其變形量最大值為4 mm，此變形量不會與周圍零部件發生干涉，滿足設計要求。應力云圖如圖12所示。

圖12非線性材料-優化后發動機吊耳應力云圖

主機廠采用優化后結構進行吊裝，發動機前后吊耳均無明顯變形，滿足要求。主機廠反饋情況與采用非線性材料的仿真結果一致，故證實采用非線性材料進行有限元分析的準確性。

僅采用材料的彈性階段屬性進行有限元分析時，當發動機吊耳所受應力超過屈服極限后，其所產生的應力均為虛假應力，遠大于發動機吊耳實際所受應力，不具有實際參考價值。因此需要采用非線性的材料屬性進行有限元分析，這樣得到結果更符合實際情況，有利于指導產品的開發與設計。

發動機吊耳僅在廠內發動機轉運和主機廠裝機時使用，在發動機全生命周期內使用次數有限，當其所受應力超過屈服極限，但未達到強度極限時，且與周邊零部件不干涉的情況下，均可正常使用。采用非線性材料分析時，當其應力超過屈服極限，但未超過強度極限時，可參考其變形量是否會與周圍零部件干涉來判斷是否滿足要求。

4 結論

通過對某發動機吊耳的強度進行有限元分析，可得到以下結論：

(1)采用彈性材料進行有限元分析時，當發動機吊耳所受應力超過屈服極限后，其所產生的應力均為虛假應力，遠大于發動機吊耳實際所受應力，不具有實際參考價值。

(2)采用非線性材料屬性得到的有限元仿真結果與主機廠反饋情況一致，證實采用非線性材料進行有限元分析的有效性。

(3)采用非線性材料分析時，當其應力超過屈服極限，但未超過強度極限時，可參考其變形量是否會與周圍零部件干涉來判斷發動機吊耳是否滿足要求。