如何利用多元表征幫助學生思維從形象向抽象過渡

李春華

中高年級學生在理解抽象的概念、公式時，常常因為缺乏直觀的形象輔助而止步不前，慢慢感覺數學越來越枯燥乏味，久而久之，容易失去數學學習的興趣。人的思維發展是由形象思維慢慢向抽象思維過渡的，小學中高年級的孩子正處于這個過渡階段，如果我們一味地割裂孩子的形象思維與抽象思維，顯然是不符合學生發展規律的。本文結合小學中高年級常見的培養孩子抽象思維的題型，以形象直觀的思維圖加以輔助，使形象與抽象相結合，力爭幫助孩子輕松突破知識難點，提高孩子學習數學的興趣，為孩子今后的長足發展夯實基礎。

形象思維是一種在人的腦海中運用具體的形象進行思考的過程。孩子的思維特點是形象思維優先。在小學數學教學中，低年級數學教材的編排主要是圖文結合的形式，比較形象，便于學生理解；中年級以后，為培養孩子的抽象思維，教材簡練了一些，如果教師還只是照本宣科，學生對抽象的概念、公式難以理解，會感覺數學越來越枯燥乏味，漸漸失去對數學的興趣。這時，我們應該怎樣繼續利用孩子形象思維優先的特點，通過圖形、圖像、符號或描述性的文字等多元表征來幫助孩子完成從形象思維到抽象思維的過渡呢？簡單來說，就是盡量做到“能畫圖的就畫圖，能舉例的就舉例。”

比如：

1.比一個數的4倍多0.1的數是1.7，這個數是多少？請列式計算。

很多學生習慣性地看到多0.1就用1.7先加0.1，再去除以4。這時，如果要求學生根據題意畫出線段圖，問題就能迎刃而解了。

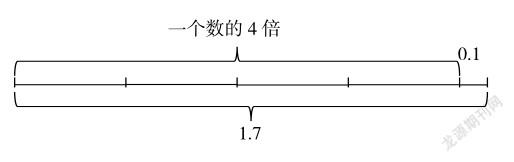
左邊部分=總數-右邊部分，即一個數的4倍=1.7-0.1，這個數的4倍是1.6，這個數就是1.6÷4=0.4。

2.（桶裝油問題）一桶油連桶重31.6千克，用去一半油后，還剩16.6千克，桶和油各重幾千克？

很多老師也知道學生理解這類題有難度，于是，找來實物在課堂上進行演示。可是，反復地演示了很多遍，會解的學生還是寥寥無幾，感覺形象思維這時候也幫不上忙了。怎么突破呢？我想，學生看老師演示，雖然明白了是怎么回事，但并不能直觀地看出桶和油之間的數量關系。如果能用一幅圖直觀地揭示它們之間的關系，學生應該也不難理解。如圖所示：

一半油：31.6-16.6=15（千克）

油：15×2=30（千克）

桶：31.6-30=1.6（千克）

是不是很直觀，簡單得多呢？

假設得數為1，那么，甲數就是10，乙數就是0.1，因此，甲數>乙數。

4.四、五年級的學生對記憶乘法分配律有困難，能不能利用形象思維來加強記憶呢？我們可以嘗試用“蜜蜂采花”或“蘋果法”來加強學生的理解。

如：2.83×2.5+2.5×1.17

這里，出現次數最多的2.5就是勤勞的小蜜蜂，花前花后采花忙，它先采了2.83這朵花，又采了1.17那朵花，把它采的兩朵花用（ ）捆起來，它就采了（2.83+1.17）這束花。這束花共4，4×2.5=10，結果就是10。

再比如：2.08×102-2.08×2

把出現次數最多的2.08看作蘋果，原有102個蘋果，減去2個，還剩100個。100個蘋果即100個2.08，就是208。

我們有些老師還根據學生特點，用“警察抓小偷”等生活事件來解釋乘法分配律，因為貼近生活，便于學生理解，也取得了顯著的效果。

我們知道，孩子的抽象思維水平越高，孩子就越優秀。但思維在從形象到抽象的過渡中，有研究表明，即使是優秀的學生也經常用直觀的方式（意象、表象等）表達抽象的概念。因此，我們可以利用多元表征使直觀與抽象形影不離，加強學生的理解，讓學生自己經歷建構概念的過程，培養學生的形象思維，讓其更好地提升教學效果教學服務。