基于力學特性量化第五腰椎受力研究

彭茂軍 任 金 周顯武 張玉友 戶佳琪 武 龍 曹明亮 賈冠偉

（1．河南大學物理與電子學院，河南 開封 475004； 2．黃河水利委員會機關服務局，河南 鄭州 450000）

0 引言

腰椎間盤突出癥（Lumbar Disc Herniation，LDH）是常見的骨科疾病，近些年發(fā)病群體逐漸趨于年輕化。由于患者一般都有腰痛、下肢活動受影響的癥狀，因此該疾病對于患者的生活和工作影響較大[1]。據國家衛(wèi)生部的最新統(tǒng)計，我國腰椎疾病患者已超過2億人，腰椎間盤突出患者占全國總人數的15.2%。目前，25歲～50歲的患者已經占患病人數的75%以上。劉俊等人[2]研究發(fā)現，80.0%的腰椎間盤突出患者存在不同程度的疼痛[3]。患者可能因為長期坐姿不正確或超負荷負重，所以椎間盤出現結構性異變，引起腰椎痛的癥狀。拐杖可以減輕使用者腰椎的壓力，從而減少腰椎磨損[4]。可以通過分析拄拐前后彎腰角度變化時，人們腰部受力變化的規(guī)律來減緩腰椎患者腰部的疼痛感[5]。郭郡浩[6-7]雖然分析了身高、體重變化對腰椎間盤的影響，但都只是在腰椎前屈角度一定的情況下建立模型，沒有分析彎腰角度對腰椎間盤受力的影響。呂永強等人[8]雖然采用脊椎復合體三維有限元模型分析了最大范式等效應力（Von Mises Stress）的變化規(guī)律，但其測試過程中所采用的Viapoint法對胸腰部肌骨模型進行構建的過程較為復雜。

由于上述腰椎間盤受力分析的方法存在分析變量單一或分析方法有一定局限性等問題，因此，該文以力學特性為基礎，在拄拐和不拄拐的條件下，以身高、體重、彎腰角度、手臂支撐角度以及身體重心為變量參數，分析第五腰椎的受力特性。通過計算得出，拄拐對緩解腰椎間盤突出的量化數據，為腰椎受力提供了指導。

1 數學模型

1.1 建模基礎

腰椎間盤退變的影像學表現主要有腰椎終板信號的異常（Modic改變）、腰椎椎間盤高信號區(qū)（High-intensity zone，HIZ）和許莫氏結節(jié)（Schmorl Node，SN）等。王本勝等人[9]的研究結果顯示，Modic改變總體發(fā)生率為26.84%，女性高于男性，發(fā)病部位主要集中于第四腰椎和第五腰椎；因此，取脊椎下端第五腰椎作為支點，以其受力情形替代腰椎疾病患者腰部受力并建立力學模型，分析不同體態(tài)腰椎疾病患者拄拐前后第五腰椎的受力變化過程，如圖1、圖2所示。

分析人體日常動作（例如彎腰）時其第五腰椎受力情況，量化其第五腰椎處所受擠壓力和剪切力的大小，對腰椎疾病患者的日常站立姿勢進行力學建模。

圖1 第五腰椎位置示意圖

1.2 不拄拐彎腰姿勢第五腰椎處受力分析

圖2 人體模型彎腰過程示意圖

腰椎疾病患者不拄拐和拄拐時第五腰椎物理模型受力圖如圖3、圖4所示，通過該模型分析第五腰椎處的受力情況。設人體模型身高為H，其中A點為第五腰椎脊神經根，將上下半身分為1∶1，B點為上軀干質心點，C點為背部骶棘肌對脊柱骨拉力的作用點，位于脊椎骨的2/3處。

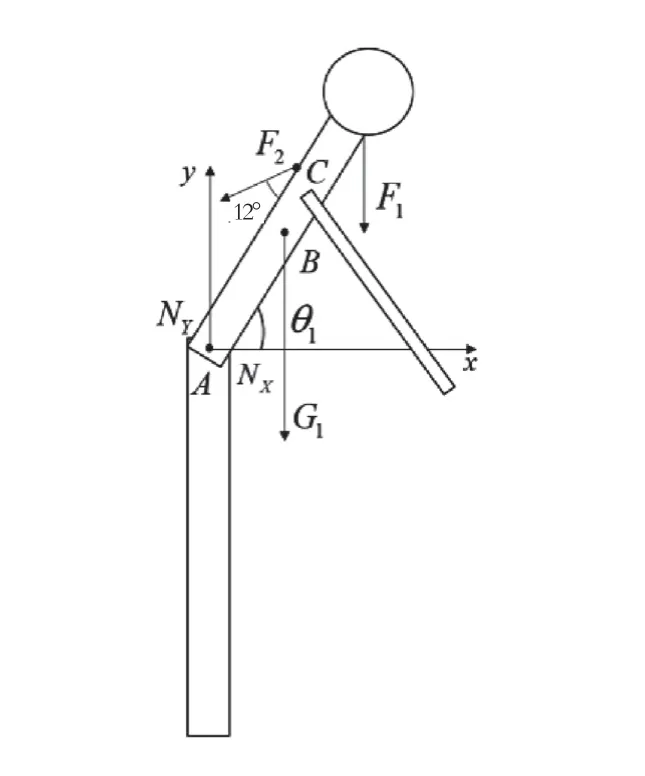
圖3 第五腰椎受力（不拄拐）

圖4 第五腰椎受力（拄拐）

將上述軀干作為研究對象，受力分析如下。

對于圖4和圖5的A點，由力的平衡方程得到表達式，如公式（1）、公式（2）所示。

式中：FX為A點水平方向所受合力，N；FY為A點豎直方向所受合力，N；NX為第五腰椎處反作用力沿水平方向的分力，N；NY為第五腰椎處反作用力沿豎直方向的分力，N；β1為受力模型沿水平方向所受合力；β2為受力模型沿豎直方向所受合力。

其中，對不拄拐腰椎受力模型建立表達式，如公式（3）、公式（4）所示。

式中：F2為背部骶棘肌對脊柱骨的拉力，N。

對拄拐腰椎受力模型建立表達式，如公式（5）、公式（6）所示。

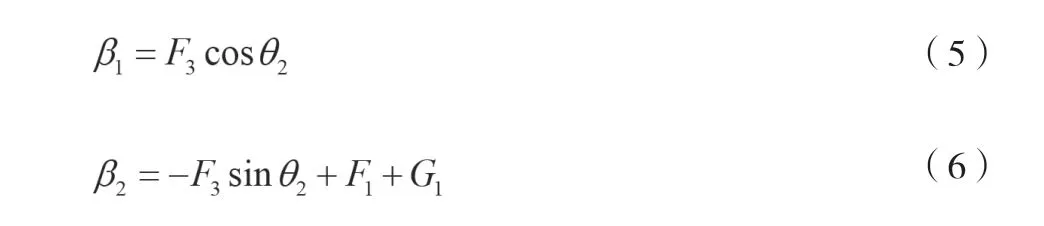
式中：F3為手臂傳遞的支持力，N；θ1為腰椎與水平線所成的角度（銳角），°；θ2為F3與腰椎所成的夾角，°；F1為頭部以及外加負載產生的力，當取人體重力為W時，其近似為0.2W；G1為上半軀干所產生的重力，當取人體重力為W時，其近似為0.4W。

在圖3和圖4中，選第五腰椎中心點A為矩心，可得表達式，如公式（7）所示。

式中：M1為上半軀干所產生的重力在A點產生的力矩，N·m；M2為頭部以及外加負載產生的力在A點產生的力矩，N·m。

列力矩平衡的表達式，如公式（8）所示。

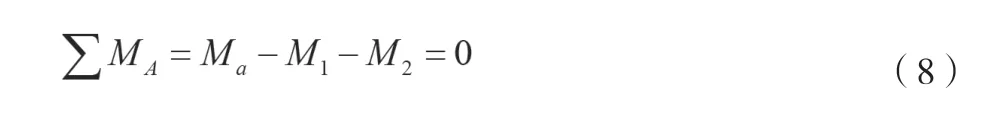
式中：MA為A點所受合力矩，N·m；Ma為手臂傳遞支持力或背部骶棘肌對脊柱骨的拉力在A點產生的力矩，N·m。

對不拄拐腰椎受力模型建立表達式，如公式（9）所示。

式中：F2為背部骶棘肌對脊柱骨的拉力，N。

拄拐腰椎受力模型的表達式，如公式（10）所示。

式中：α為支持力位置比，即第五腰椎到C點距離與C點到頭部距離的比值。

進一步聯(lián)立上式求解第五腰椎處所受合力N的大小，如公式（11）所示。

式中：k為上軀干重心G1到頭部的距離與到第五腰椎處的距離的比值；θA為合力在A點與水平方向的夾角，°；θN為手臂傳遞支持力或背部拉力與垂直于腰椎方向的夾角，°。

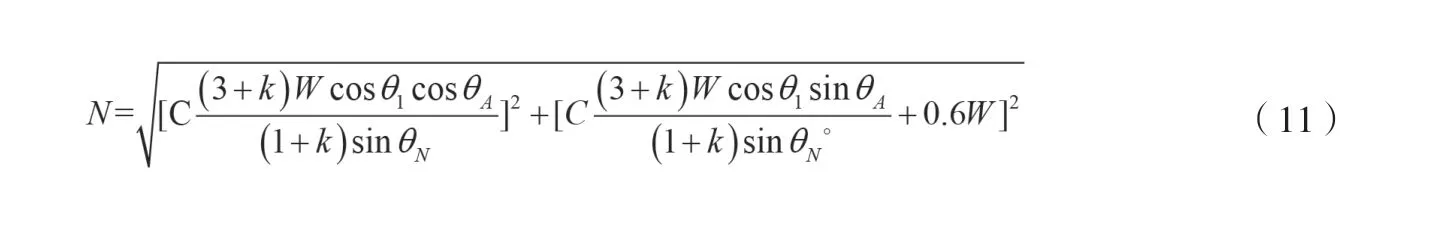
其中，C為腰椎受力系數。患者不拄拐時，C為固定值；拄拐時，C是與支持力位置比α有關的變量。

2 結果與討論

2.1 拄拐前后不同體重腰椎疾病患者第五腰椎處受力

以腰椎疾病患者的體重為自變量，彎腰角度θ1分別固定為30 °、40 °和50 °，手臂傳遞的支持力θ2固定為70 °，重心位置比K固定為1，支持力位置比α固定為0.6，計算分析拄拐以及不拄拐時其腰部的受力數據。

如圖5所示，隨著患者的體重由50 kg逐漸增加，其腰椎受力呈增大的趨勢；但是拄拐時的腰椎受力明顯小于不拄拐時的腰椎受力。當彎腰角度保持30 °，體重從55 kg增加到70 kg時，不拄拐時的腰椎受力從690 N增加到1180 N，拄拐時的腰椎受力僅從126 N增加到162 N。因此，對于不同體重的腰椎疾病患者，拄拐可以有效地幫助其緩解腰椎的受力大小。

圖5 不同體重下第五腰椎的受力

2.2 拄拐前后彎腰角度θ1變化時第五腰椎處受力

為了更好地表現彎腰的程度，以與腰椎疾病患者彎腰角度θ1互余的角度θ3為自變量，體重固定為60 kg，手臂傳遞的支持力θ2固定為70 °，重心位置比K分別設定為1、1.1和1.2，支持力位置比α固定為0.6，計算分析拄拐前后不同彎腰角度對應的腰部受力數據。

如圖6所示，當身高和角度θ3逐漸增加時，腰椎受力也會逐漸增大。拄拐時的腰椎受力明顯小于不拄拐時的腰椎受力。當重心位置比K為1.2，角度θ3從30°增加到70°時，不拄拐時腰椎受力從1178 N增加到1510 N，而拄拐后腰椎受力僅從136 N增加到193 N。因此，拄拐可以有效地幫助腰椎疾病患者在彎腰過程中緩解腰椎的受力情況。

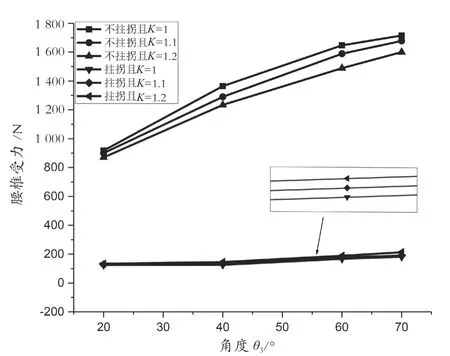
圖6 不同彎腰角度下第五腰椎的受力

2.3 拄拐前后重心位置比K變化時第五腰椎處受力

以重心位置比K為自變量，體重固定為60 kg，彎腰角度θ1固定為60°，手臂傳遞的支持力θ2固定為70°，支持力位置比α固定為0.6，計算分析拄拐前后不同重心位置比K對應的腰部受力數據。

如圖7所示，隨著重心位置比K逐漸增加，腰椎受力呈現平緩的趨勢，不拄拐時腰椎受力略有下降，但是拄拐時的腰椎受力明顯小于不拄拐時的腰椎受力。根據上述已知條件，重心位置比K從0.8增加到1.2，不拄拐時腰椎受力從1200 N減小至1120 N，拄拐后腰椎受力大小僅從143.5 N增加到到158.0 N。

圖7 不同重心位置比的腰椎受力

2.4 拄拐時手臂支持力角度θ2變化時第五腰椎處受力

下面分析只在拄拐時出現的參量θ2。以手臂支持力角度θ2為自變量，體重固定為60 kg，彎腰角度θ1固定為60 °，重心位置比K固定為1，支持力位置比α固定為0.6，計算分析不同腰椎疾病患者拄拐時手臂支持力角度θ2對應的腰部受力。

如圖8所示，隨著手臂支持力角度θ2的增大，腰椎疾病患者在拄拐時腰椎受力在不斷減小。而θ2的大小與手臂長度以及身高有一定的聯(lián)系，手臂越長或身高更高的腰椎疾病患者，其拄拐時手臂支持力角度θ2相對較小。拄拐時當手臂支持力角度θ2從60 °變化到80 °時，腰椎受力大小從210 N減小至84 N。因此，手臂長度和身高也對腰疾病患者拄拐時腰椎受力的大小產生影響，腰椎疾病患者的手臂越長或身高越高，其拄拐時腰椎受力越大。

圖8 手臂支持力角度θ2對腰椎的受力

2.5 拄拐時支持力位置比α變化時第五腰椎處受力

以支持力位置α為自變量，體重固定為60 kg，彎腰角度θ1固定為60 °，手臂傳遞的支持力θ2固定為70 °，重心位置比K固定為1，計算分析不同腰椎疾病患者拄拐時支持力位置比α變化時對應的腰部受力數據。

α與身高成正比關系，其表達式如公式（12）所示。

式中：H為身高，cm。

由于當身高H從150 cm增加到175 cm時，支持力位置α從0.50增加到0.70；因此，隨著身高的增加，支持力位置α也逐漸增加。根據上述條件，擬合支持力位置α與腰椎受力的函數關系，可知腰椎受力為-90α+206 N。如圖9所示，由于當支持力位置比α從0.50變化到0.70時，腰椎受力大小從161 N減小到143 N；因此，隨著支持力位置比α逐漸變大，腰椎受力就會逐漸減小。

3 結論

腰椎間盤疾病是中老年人以及青年人的常見疾病，對日常生活產生了嚴重的影響。該研究對人體第五腰椎建立了力學模型，分析了拄拐對腰椎間盤的受力影響，得出以下4條結論：1） 彎腰角度增大時，腰椎受力呈增大的趨勢，例如當體重50 kg的腰椎疾病患者彎腰角度為40 °時，拄拐時腰部受力僅為120.6 N，遠低于不拄拐的1234.6 N。2） 隨著角度θ3逐漸增加，腰椎受力也呈增大的趨勢。當彎腰角度70°、重心位置比K為1時，拄拐時腰部受力僅為182 N。3） 在固定其余參數的條件下，隨著重心位置比K的逐漸增加，腰椎受力由143.5 N變化到158 N，呈現平緩的趨勢；不拄拐時腰椎受力下降到1120 N。4） 拄拐時手臂長度和身高也對腰椎疾病患者腰椎受力產生影響。手臂支持力角度θ2減小時，腰部受力增大；支持力位置比α減小時，腰部受力也會增大。

圖9 支持力位置比對腰椎的受力