基于蟻群算法的廢液排放系統管路布局優化

孫冠宇 黃 捷 夏軍寶 蔡鼎陽 干依燃

（中國核動力研究設計院核反應堆系統設計技術重點實驗室，四川 成都 610041）

0 引言

網絡是社會的重要組成部分，例如，天然氣管道、污水管道、配電系統、電信網絡等物理網絡。 這些網絡普遍具有建設成本高、建設過程復雜、不易優化等特點，因此大量學者對此類網絡的布局優化問題進行了研究。例如，Argaman[1]等人使用DP 方案對重力污水管道網絡的優化設計進行了簡化，但只適用于自然地形中管道出口方向傾斜的理想狀況。 除此之外，Walters[2]也使用了DP 方案對污水管道的布局和尺寸進行了優化，使次管網可以從一組固定的排放源排出污水。 Li[3]提出了優化城市污水管網的嵌套方案，但對計算量的要求較高。Jang[4]利用離散差分動態規劃設計城市污水管網最優布局模型，但忽略了管網尺寸的優化。 Diogo與Graveto[5]提出了一種“枚舉+模擬退火”的模型，對污水管道網絡的布局和規模大小進行了優化。

上述學者已經提出了大量關于污水管道布局的優化方案， 本文針對核電轉換系統的廢液排放管道，通過類比分析，綜合考慮管網設計設計中布置走向要求特殊、管網規模復雜等問題，提出廢液排放管道的布局優化要求與規模優化需求， 結合ACOA 與TGA算法，設計了廢液排放管道網絡布局和組件尺寸優化的解決方案，并將此方案的性能與ACOA 方案進行了測試對比，結果表明，該方案較ACOA 方案能夠更好地解決廢液排放管道網絡的布局和規模確定問題。

1 廢液排放管網的設計問題

廢液排放系統通常由管道、集水井、排水泵以及其他附屬設施組成，用于收集核電轉換系統管道疏水和設備檢修時的排水。廢液排放管道網絡優化首先需對廢液排放管道網絡布局進行設計，使其符合接口數量、系統布局以及布置區域要求，然后對其進行規模設計，定管道尺寸、布置高度以及其他特定設計參數。

一般來說，廢液排放管道網絡的聯合布局和規模尺寸確定的問題，可以在數學上定義為確定每個管道的管道連接、直徑和布置高度的問題，從而管道網絡建設成本的最小值為：

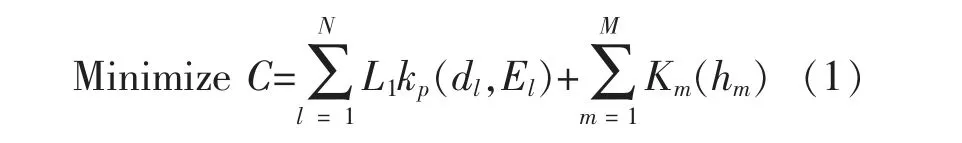
式中，C 為廢液排放管網的成本函數；N 為管道總數；M 為支吊架總數；L1為管道l 的長度（l=1， …，N）；kp為安裝管道的單位成本，取決于管道直徑dl和平均布置高度El；Km為支吊架的建設成本，其主要取決于支吊架所在管線的布置高度hm。

上述網絡建設成本受拓撲以及液壓的制約因素如下[8]：

（1）廢液排放管道的平均布置高度需在最大和最小高度定義的范圍內，即：

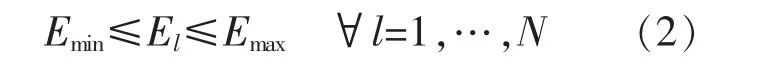
式中，Emin為污水管道的最小布置高度；Emax為最大布置高度；El為平均布置高度；N 為此管網分段安裝的總數。

（2）需確保廢液排放管道能夠以不超過最大允許速度的速度輸送廢液，以防止管道腐蝕；管道流速應至少每天一次大于自清潔速度，以防止雜質沉積在管道底部：

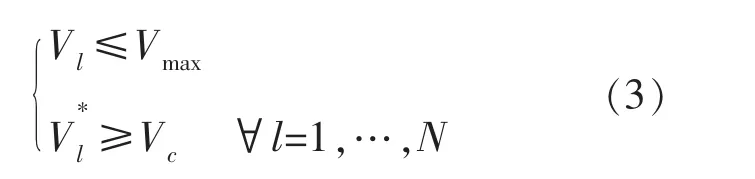
式中，Vl為在設計流量下管道l 的流速；為開始時管道l 的最大流速；Vc為管道的自清潔流速；Vmax為管道的最大允許流速。

（3）排放管道應考慮最小坡度，以免因施工不正確而造成不利的坡度：

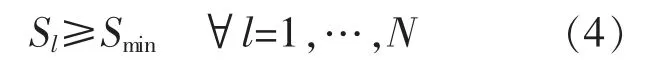
式中，Sl為管道l 的斜率；Smin為管道的最小坡度。

（4）為避免增壓流和管道中雜質的沉積，應考慮最大和最小相對流量深度：

式中，dl為管道l 的直徑；yl為管道l 的水深；βmax為允許的最大相對流深；βmin為允許的最小相對流動深度。

（5）排放管道直徑應從通用管道直徑中選擇：

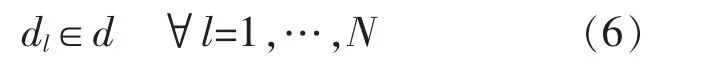
式中，dl為管道直徑；d 為通用管道直徑的離散集合。

（6）滿管的情況下，為避免增壓流的情況需評估管網的水力參數：

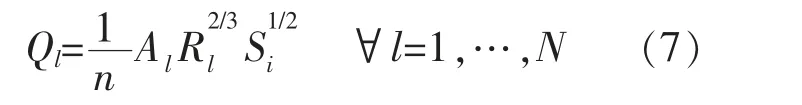
式中，Ql為管道l 的排放量；Al為管道濕橫截面積；Rl為管道水力半徑；n 為曼寧常數；Sl為管道坡度。

（7）管網中的管道，離開匯聚點處的排放管道直徑不得小于進入匯聚點處管道的直徑：

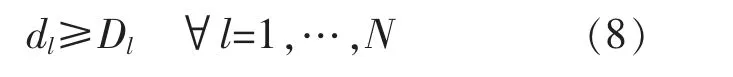
式中，dl為離開匯聚點處的管道直徑；Dl為進入匯聚點處的管道直徑集合。

（8）呈樹狀結構形式的管網，根節點代表出口，非根節點表示檢修孔， 節點到葉子的邊代表網絡的管道。在樹狀結構中，為確定管道布局的形式，限制每個節點只能從一條邊離開，其數學定義為：

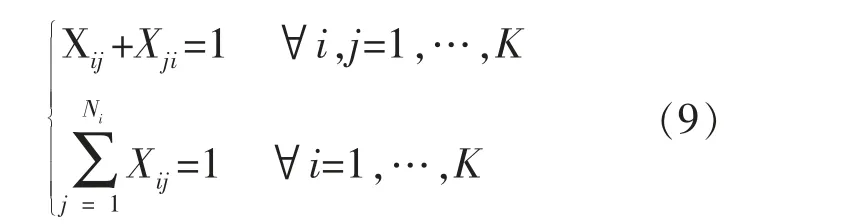
式中，Xij為二進制變量， 當管道從節點i 流向節點j 時為1， 否則為0；Ni為連接到節點的管道數，K為節點總數。 考慮到管網中節點i 的連續性，因此：

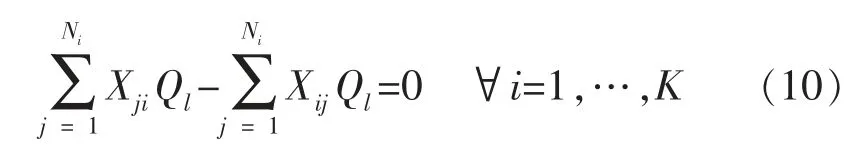
式中，Ql為在節點i 和節點j 之間管道l 的排放量。

從以上的分析可知，廢液排放管網的設計問題實際是一種混合整數非線性規劃問題，此問題的復雜性來源于約束（9）和（10）。 設計最佳的解決方案需要更系統、有效的方法來實施約束，因此，本文采取了基于ACOA 算法改進的方案來進行解決。

2 AC O A- TG A 解決方案

ACOA[7]的基本思路是假設存在一群人工螞蟻，這些螞蟻可以通過間接通信尋找到從蟻巢到目的地的最短路徑，并且蟻群之間會相互合作從而尋找最優的解決方案，但是此方案并不會考慮路徑的規模大小。

在ACOA-TGA 的布局方案中，ACOA的增量構建功用于確定管網規模，TGA 則用于限制螞蟻路徑只能形成樹狀布局。ACOA-TGA 布局方案中的節點為決策點，決策點由所有管道的直徑集合所定義，同時TGA在每個決策點定義形成樹狀布局，可以此方案中新決策點的選項數量都可以由舊決策點的決策來確定。 如圖1 所示， 其中圓圈代表網絡節點， 黑體圓圈代表ACOA 的決策點，圓圈中的數字代表節點編號，括號中的數字表示管道編號， 表示將用于管道的直徑集合，方括號表示在每個決策點螞蟻可用于形成樹形布局的選項，并且表示螞蟻選擇了的直徑，使得正在構建的樹中包含管道，并自動將管道的另一個節點定義為下一個決策點。

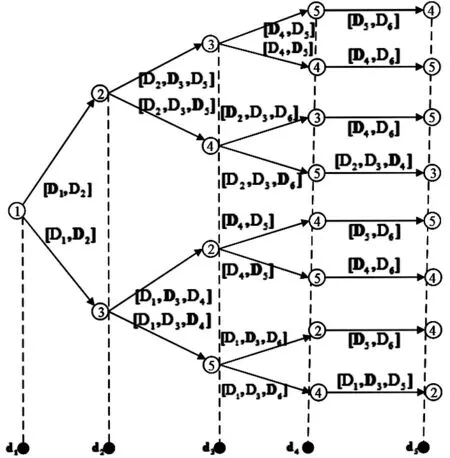
圖1 ACOA-TGA 典型問題解決方案

但是，使用該方案可能會違反上述（2）～（10）中的約束，所以，為鼓勵螞蟻做出不違反約束的解決方案決策，可通過懲罰機制來完成，定義解決方案成本[6]如下：

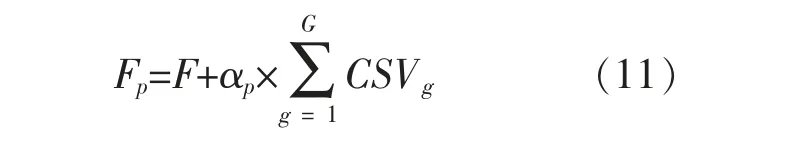
式中，Fp為懲罰成本函數；F 為原始成本函數；CSVg為違反約束的度量；G 為約束總數；αp為懲罰常數。 如果懲罰常數足夠大，那么任何的不可行方案的成本都將大于可行方案的成本，從而約束螞蟻的可行性選擇。

3 測試結果與分析

本文使用大小為400 m×400 m 的四邊形區域所需的廢液排放管網對所提出算法的性能進行了測試，假定該區域的接口在設計開始階段和結束階段都均勻分布在該區域，分別為每公頃2 500 和4 000 個。整個設計過程中， 每個接口每天的平均廢液量上限為250 L/d；假定最大管道水流量系數為2.8，最小管道水流量系數為0.6。

如圖2 所示， 次測試示例具有25 個節點和40條邊界，管道直徑范圍為100～1 500 mm；規定100～1 000 mm 的間隔為50 mm，1 000～1 500 mm 的間隔為100 mm；網絡的管道長度恒等于100 m。 由于測試示例為假設，因此，此解決方案的其他參數[13]為：接口配置系數n 為0.015；Emax為10 m；Emin為2.5 m；βmax為0.83；βmin為0.1；Vc為0.75 m/s；Vmax為6 m/s。 因為在管道安裝中，需考慮安裝支吊架的費用，因此本文借鑒使用Afshar 等人提出的管道安裝成本[7]：

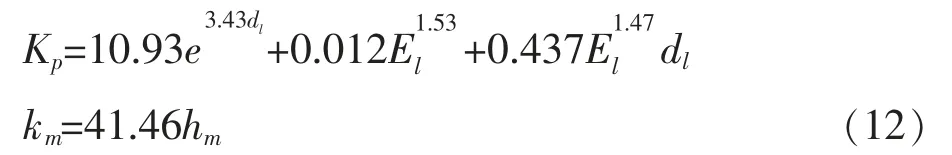
本文分別使用ACOA 方案和ACOA-TGA 方案對以上案例進行了測試， 下圖3 為該測試例的ACOATGA 最佳樹狀布局。

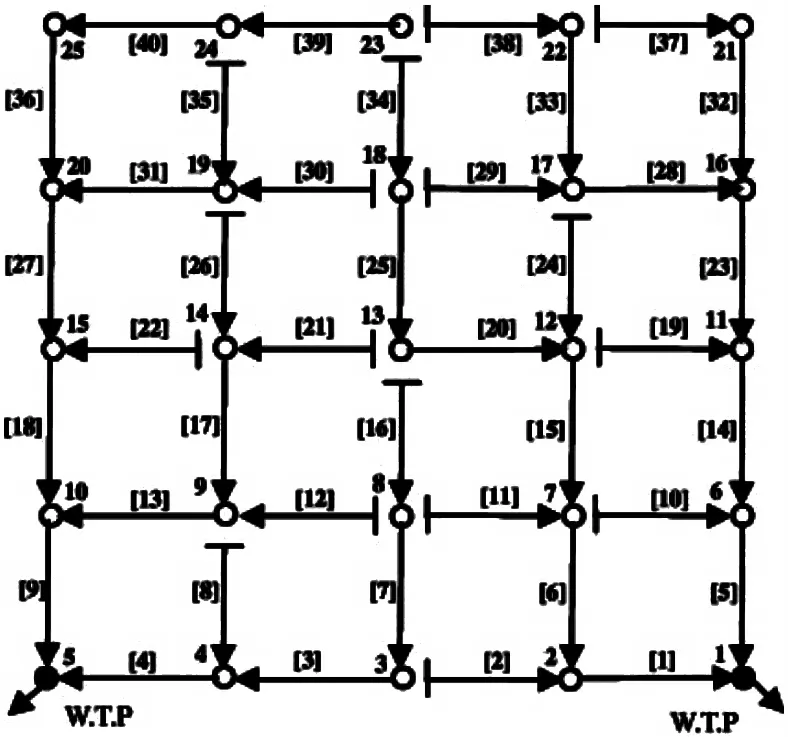
圖2 ACOA-TGA 最佳樹狀布局方案

表1 顯示了使用生成的測試示例隨機運行10 次的結果，以及縮放后的標準偏差，十次運行中產生的最終解決方案成本的標準偏差以及可行的最終解決方案數量。由表1 可知，使用ACOA-TGA 方案可以改善最終解決方案中的最小成本，最大涂層，平均成本以及標準差。

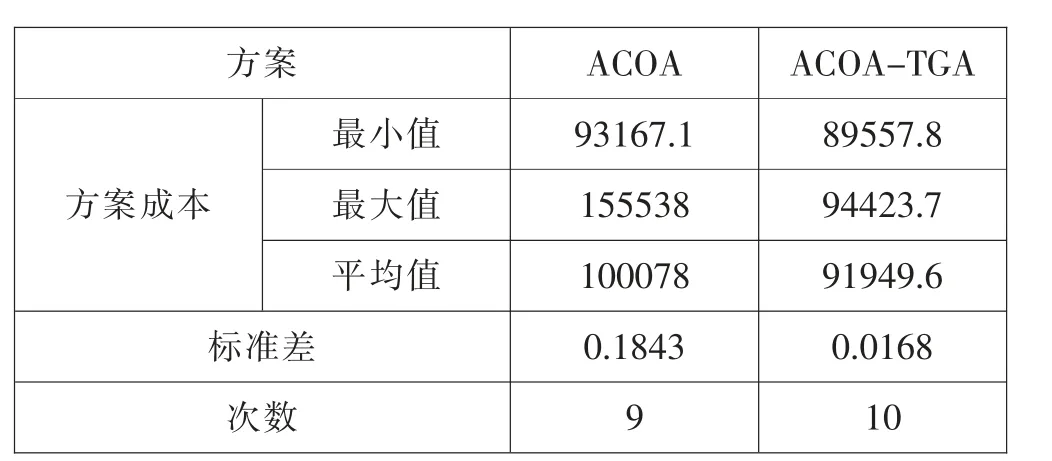
表1 10 次運行的測試結果

4 結語

在本文中， 參考了傳統工業中污水管網的布局優化問題和規模確定問題， 結合核電轉換系統的廢液排放特點， 設計了基于ACOA 方案的改進方案ACOA-TGA。 在傳統的ACOA 布局方案的基礎上，使用TGA 對管網的規模進行了限制，構建了可行的樹狀布局。 并對ACOA 和ACOA-TGA 方案分別進行了性能測試和結果比較。結果表明，ACOA-TGA 方法能夠較好地解決廢液排放系統管道網絡的布局和規模確定問題。