求解并行JSP 作業車間調度問題的一種混合遺傳算法
方 霞, 俞宏圖, 熊 齊
(湖南文理學院, 國家Linux 技術培訓與推廣中心, 湖南 常德 415000)
0 引言
企業制造核心JSP 問題 (Job-Shop Scheduling Problem 作業車間調度)需要人員、物料、設備等多種資源優化整合,涉及到各類生產要素,具有數據量大、種類繁多的特點,同時加工任務也具備多品種、多批量、多工序、多任務等特征, 如何有效提高資源的利用率, 縮短加工周期、合理規劃工件各工序的加工流程一直是研究的熱點。
JSP 問題是NP 難問題,為了改進調度性能,一些學者進行了研究,提出了很多解決方案,得到了很多有意義的結論: 程八一采用作業分類策略產生候選表和輪換法對信息素更新提高算法效率[1]。 宋存利提出采用基于工序的隨機鍵編碼的一種混合微粒群算法HPSO 有效改進大多數經典調度問題[2]。 蔣南云等建立了雙層生產計劃與調度集成優化隨機期望值模型[3]。 徐本柱設計了同工件同批工序間、不同工序間的并行調度算法,使分批具有方向性和預測搜索空間[4]。 Xiao-long Zheng,Ling Wang 提出了基于知識的果蠅優化算法KGFOA[5],對于并行調度JSP 問題都有一定積極改進意義。
本文針對并行任務JSP 問題進行了更深一步的探究,結合JSP 問題的實際應用多樣性和復合型,設計優化的底層染色體結構,嵌入可行解檢測判斷,生成動態生產調度表,混合遺傳算法求解,得到更高效的并行調度JSP 問題求解方案。
1 作業車間調度數學模型
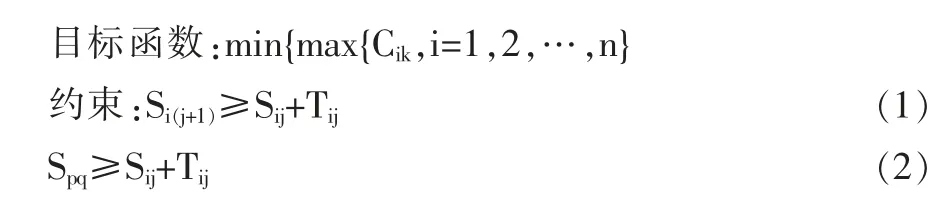
(同一臺機器上,Oij在Opq之前加工)
約束條件(1)和(2)分別表達對應滿足條件,其中基本符號說明:Cik—工序Oij在第K 臺機器上加工完成時間;Sij—工序Oij的開始加工時間;Tij—工序Oij的加工時間(假定加工時間已經融合了存儲、裝卸、搬運和等待加工等準備環節, 不再另外標注相關等待時間);Ji—工件i(i=1,2,…,n);Mi—機器i(i=1,2,…,m);Oij—工件i 的第j 道工序。
2 求解并行JSP 問題的混合遺傳算法
2.1 染色體編碼
為了方便表達調度及其甘特圖采用工序順序碼。 工序總編號:統一對所有工序從小到大依次進行順序編號。染色體基本信息表中每一條記錄由五項基本信息構成:工序總編號/工件號/工序號/機器號/加工時間,如3/2/1/5/6 基因信息,分別表示總工序號為3,第2 個工件第1 道工序在機器5 上需加工時間為6(單位)。
2.2 生成初始可行解
JSP 問題求解是NP 難問題, 找到全局最優解不容易,求解時需要防止收斂速度過快而陷入局部最優解,初始要盡量使得染色體具備多樣性。 采用蟻群算法隨機性好、初始解均勻分布的特點,生成多種初始種群,具體實施步驟如下:
算法1:生成初始可行解
步驟1:設置種群數量N。 步驟2:對于染色體i,隨機拋灑螞蟻于總工序號編碼位置,得到一組隨機調度,這時還不能保證解的可行性。 步驟3:依次在染色體基本信息組成表中查詢和染色體i 的總工序號對應的工件號,得到該染色體的工件編碼,填入工件號j。 步驟4:根據染色體i 的工件號j,啟動可行解檢測子程序(算法2),調整得到具備可行解特征的染色體。 步驟5:根據染色體i 的工件號j 及其工序號,查找染色體基本信息表,得到相應的機器和加工信息。步驟6:重復步驟2~5,直到N 條染色體全部信息設置完成。
2.3 可行解檢測
JSP 問題中如何保證可行解工序編碼是調度任務完成的首要任務,本文中的可行解檢測調整算法具體步驟如下:
算法2:可行解檢測
步驟1:對生成的動態調度信息表,將工件i 的所有工序順序編碼,從1 開始依次填入其所有工序號j。 步驟2:篩選動態調度表的工件i 的所有工序j 信息,比對染色體基本信息表, 根據基本信息表的安排重置動態調度表的總工序號,使之成為可行解。 步驟3:根據總工序號,對動態調度表的機器編碼、加工時間等信息進行匹配,保持數的一致性。 步驟4:對所有工件執行上述步驟,使動態調度信息生成為可行解。
2.4 選擇算子
適應值函數:根據最小最大完工時間數學模型,對當前調度方案中每一條染色體分別進行操作, 根據當前工件的工序號, 查找對應選中機器的最早可以加工時間和當前工序的最早可以加工時間, 兩者的最大值便是當前工序的最早開始加工時間。 調度方案中所有工序中最大的加工完成時間即為該調度方案的適應值結果。
每一次迭代適應值函數計算得到最小最大完工時間值,為當前各個調度方案的最好解,保留。 對所有種群的每一條染色體計算適應值函數值,采用錦標賽機制,兩兩比較,適應值優越的染色體保留下來。
2.5 交叉算子
采用隨機選中工件實現交叉操作: 對動態生成的調度表,在執行可行性檢測調整之前,首先在種群中任選兩個染色體為父代,隨機挑選生成交叉操作的工件號。具體交叉操作如圖1 所示: 父代1 的該工件所有工序保持不動, 其余的工件順序和父代2 的對應工序進行交叉依次填入,得到子代1;父代2 的操作反之亦然,得到新的子代2。 然后將交換更新的子代進行可行解檢測調整,匹配每一個工件對應的工序號、機器編號及加工時間,得到新的子代可行解。算子中采用隨機設置工件固定,以及順序交叉鄰域搜索策略,使得解的多樣性性均得到充分保證。
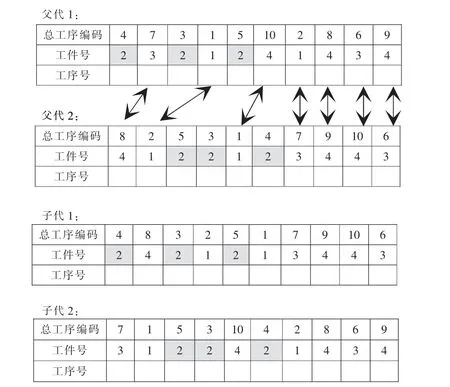
圖1 交叉操作
3 改進的混合遺傳算法
針對并行JSP 作業車間調度問題,綜合上述的選擇、交叉、變異算子的各項描述,總體的混合遺傳算法描述如下:
算法3:改進的混合蟻群算法求解JSP
步驟1: 根據工件加工工序的先后建立相應的AOE工序排序析取圖;步驟2:根據初始數據,生成工序總編號,以及染色體基本信息表;步驟3:采用蟻群算法生成N條染色體初始種群(算法1),得到動調度信息;步驟4:對每一條染色體進行可行解檢測調整(算法2),得到可行調度方案;步驟5:計算適應值函數,得到當前迭代生成調度的最優適應值,并保留;步驟6:選擇適應值優越的染色體保留;步驟7:進行交叉操作,得到新的子代種群;步驟8:以一定概率進行變異操作,得到新的子代。
重復執行步驟5~8, 直至滿足迭代次數要求,或者迭代超過20 次結束迭代。
4 實驗仿真
實驗環境仿真平臺采用MATLAB 編程實現,針對國際通用數據ft06 問題檢測,其相關收斂特性如圖2 所示,能夠快速找到目前已知最優解。
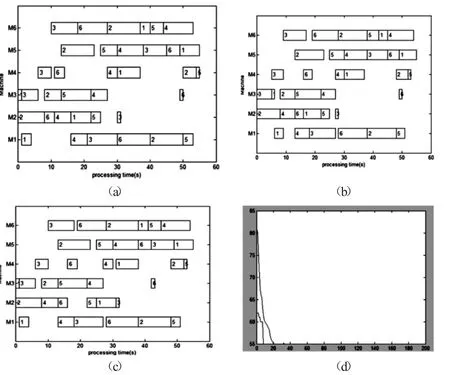
圖2 Ft06 問題實驗調度信息及收斂效果
5 結束語
對于并行JSP 作業車間調度問題,設計了高效的染色體基本結構,較好避免產生非可行解的可能性;同時選擇蟻群算法, 加大解的搜索空間, 構造好的初始解種群。 然后通過融合遺傳算法的選擇、交叉、變異等操作,較好實現了JSP 作業車間調度的優化,從而提高找到全局最優解的效率。 通過國際通用數據實驗證明,改進混合遺傳算法能夠有效提高并行JSP 作業車間調度問題的求解。

