基于維修經濟性的重載鐵路大機搗固最佳時機決策方法
徐菲 曲建軍 秦懷兵
(1.中國鐵道科學研究院集團有限公司基礎設施檢測研究所,北京 100081;2.朔黃鐵路發展有限責任公司,河北肅寧 062350)
大型養路機械(簡稱大機)搗固作為有砟軌道線路維修的主要形式之一,能夠有效改善線路的平順性,保證列車安全、平穩運行。隨著經濟維修理念深入人心以及大機維修經驗不斷積累,大機搗固作業正向更加精細化和經濟性的方向發展。工務部門希望從影響大機搗固作業效果的諸多因素中尋找可控因素,以量化比較不同維修模式對大機搗固作業效果的影響,力求在保證線路質量的同時盡可能提高大機搗固作業效率,降低維修成本。因此,大機搗固維修決策應在綜合考慮維修成本、維修效率等因素基礎上選擇適當的維修時機。
曲建軍[1]基于灰色G(1,1)理論結合不同維修模式的軌道質量恢復模型,預測不同搗固模式下的搗固作業周期,為大機維修時機的確定提供依據。徐偉昌[2]通過建立搗固作業質量預測模型與搗固維修決策模型,提出以線路維修服務水平確定搗固維修作業維修時機的方法。以上研究均未考慮維修成本。邱俊興等[3]提出以軌道質量指數(Tamping Quality Index,TQI)和維修作業成本的比值評價維修作業的經濟性,并求解最經濟維修時間以確定大機搗固時機,但未考慮不同搗固維修模式對維修后線路質量和維修成本的影響。
本文根據重載鐵路工務維修現場需求,綜合考慮搗固維修經濟性和不同維修模式對大機搗固效果的影響,引用線路質量與維修作業成本綜合評價指標決策理念,提出以線路品質指數表征線路質量,以不同搗固模式的維修費用與維修質保期(搗固周期)綜合考慮維修成本,結合搗固周期線性預測方法,求解線路區段不同維修模式下的最佳搗固時機,使線路質量和維修成本達到最優平衡點,以實現在保持較好線路質量的同時降低維修成本的目的。
1 基于MTQI的線路品質指數
大型搗固機械通過搗鎬的振動作用促使枕下石砟重新排列,主要用于成段改善高低和軌向不平順,對軌距的改善效果并不明顯[1]。因此,對TQI 進行改良,采用MTQI(Machine Tamping Quality Index)作為搗固維修前后軌道質量的評價指標,計算公式為

式中:對于i=1,2,…,6,σi分別為左高低、右高低、左軌向、右軌向、水平、三角坑6 項檢測數據的200 m 標準差。
由于不同速度等級的MTQI 管理值不同,憑借MTQI 值不能直接評價不同速度等級線路質量的優劣程度,且MTQI 值越大時線路質量越差,二者并非正相關。因此在MTQI 評價方法的基礎上,采用線路評分方法,提出一個表征線路質量得分的指標,即線路品質指數Q,將各速度等級的MTQI值通過相應的公式轉換為0~100 的不同分值。當MTQI 值為0 時,Q= 100,此時線路狀態最佳;當MTQI 值等于或超過相應速度等級的管理值時,Q= 0,表示線路質量得分為0。線路品質指數Q的計算公式為
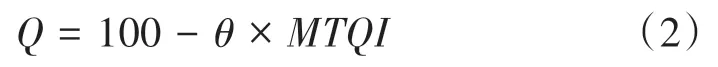
式中:θ為轉換系數。
θ的取值根據不同速度等級的MTQI 閾值確定。TG/GW 102—2019《普速鐵路線路修理規則》[4]中各速度等級的MTQI 管理值為一個取值范圍,因此采用其中一個中間值作為MTQI 的閾值。工務維修部門也可根據線路實際情況,確定相應的MTQI 閾值。MTQI 閾值與θ的取值見表1,其中vmax表示最大速度。

表1 普速鐵路各速度等級MTQI閾值及θ取值
2 重載鐵路不同搗固模式軌道質量恢復模型
文獻[1,5-6]中,基于多條有砟軌道的搗固車型、搗固作業插鎬方式、搗前測量方式、搗后穩定形式等不同搗固維修模式實測數據,分析大機搗固前后MTQI 值分布規律,得出了不同大機搗固模式下的軌道質量恢復模型。對于重載鐵路大機搗固模式:單插不穩定/人工測量/09-32 型車(模式1)和單插+單插不穩定/人工測量/09-32 型車(模式2),其軌道質量恢復模型見圖1。圖中標出了離散數據的95%置信區間,即-yi+ 2σ,其中-yi表示MTQI 的平均值,2σ表示MTQI的標準差。Ⅱ為趨勢擬合值,Ⅰ和Ⅲ分別為最大、最小95%置信界限。
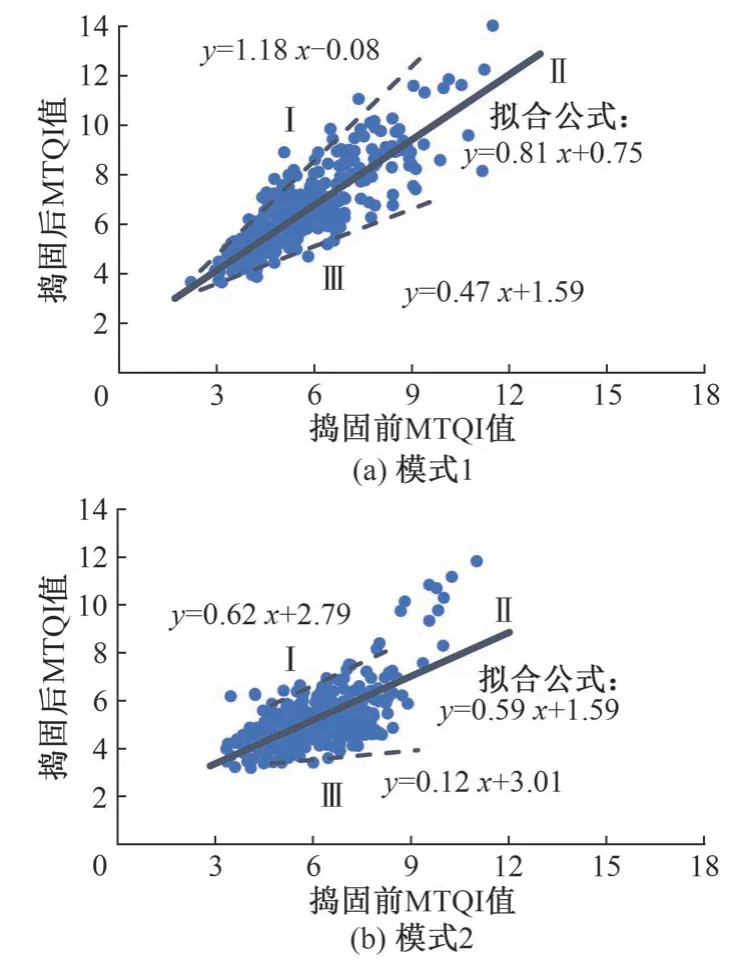
圖1 軌道質量恢復模型
3 最佳搗固時機決策方法
有砟線路周而復始地經歷著惡化-維修-惡化的循環過程。采用A 和B 兩種不同搗固維修模式,線路質量恢復程度不同,維修周期也存在差異,見圖2。
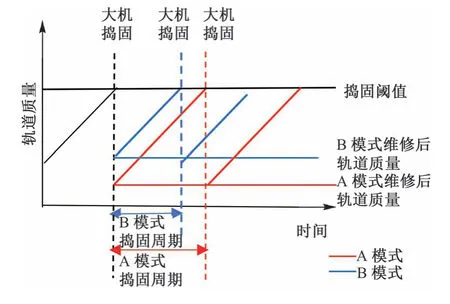
圖2 有砟線路軌道質量發展過程
更好的線路質量通常須花費更多的維修費用,若減少維修費用則維修質量勢必下降,因此須尋求線路質量與維修成本的一個最佳平衡點。以二者的比值作為綜合評價指數α,即
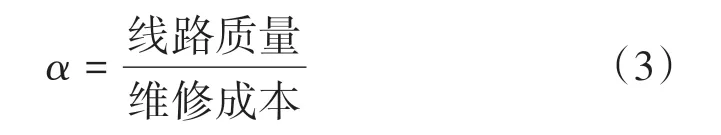
當線路質量越好、維修成本越低時,α越大。α最大時即為經濟維修的最佳搗固時機。選擇在此時進行搗固維修,可以使維修后的線路質量和維修成本達到一個最佳平衡點,使得維修性價比達到較高水平。為定量分析α,須對線路品質和維修成本加以定義。
3.1 線路品質
大機搗固維修作業以后,線路質量隨時間不斷惡化直至下次維修,因此采用搗固后線路品質指數Q的平均值代表搗固維修后的整體線路質量。假設搗固前的MTQI 值為M,搗固后的MTQI 值為N,根據圖1 中不同搗固模式下的軌道質量恢復模型,可將N表示為M的函數,r表示不同搗固模式,則搗固后至下次搗固之前的線路品質可表示為
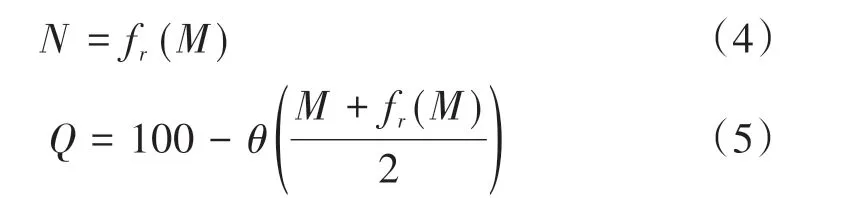
3.2 維修成本
對于某區段,假設某種維修模式投入的費用為βr(單位:萬元/km),搗固周期為T(單位:d),則平均年須搗固次數為365/T,若區段長度為L(單位:km),則每年搗固作業的成本C可表示為
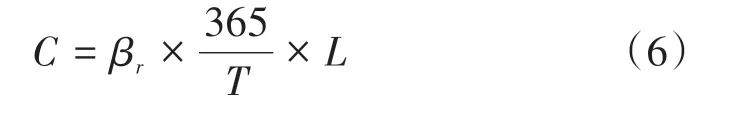
3.3 搗固周期
在同一搗固周期內,軌道幾何不平順隨時間的變化可以近似為線性發展[7-8]。基于軌道不平順動態檢測數據,利用單位時間內軌道幾何不平順幅值的變化量來評價軌道狀態變化的快慢程度,是目前應用較為普遍的一種軌道質量線性預測方法,計算公式為
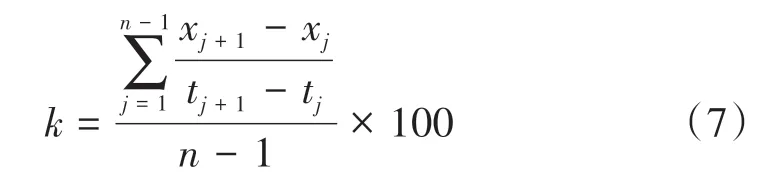
式中:k為第1 次檢測到第j次檢測時間段內軌道幾何不平順百天變化率,mm/(100 d);xj為第j次軌道幾何不平順檢測值,mm;tj為第1 次檢測到第j次檢測的時間間隔,d;n為有效檢測次數。
搗固周期T可表示為M和N的函數,結合式(4),可表示為
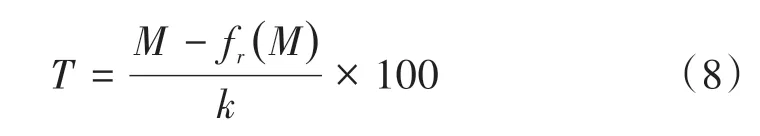
綜上所述,綜合評價指標α可表示為
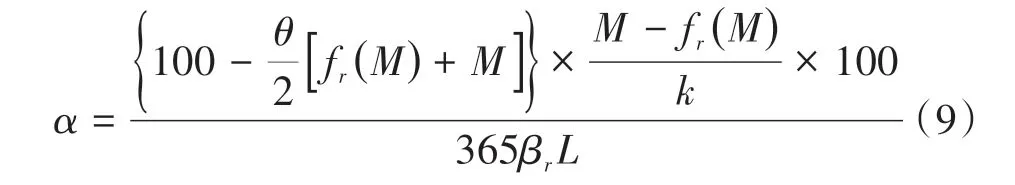
確定區段采用某種搗固模式的最佳搗固時機實質是求解關于M的二次函數的最值問題,即求解使得α為最大值αmax時的M(記為Mmax)。當區段的MTQI 值等于Mmax時即為最佳搗固時機,Mmax為最佳搗固閾值。
4 重載實例分析
以某重載線路重車線K250—K270 區段(速度等級120 km/h)2020年1月為例。一個天窗點內大機搗固作業里程約為2~4 km,選擇2 km 為一個搗固單元,將實例區段按里程劃分為10個搗固單元,各搗固單元某次檢測數據的MTQI 值通過求單元內該次檢測的各200 m MTQI值的平均值得到。
通過歷史軌道檢測數據計算各搗固單元的歷史MTQI 值,并結合維修信息計算k。各搗固單元當前MTQI值(2020年1月)及k見表2。
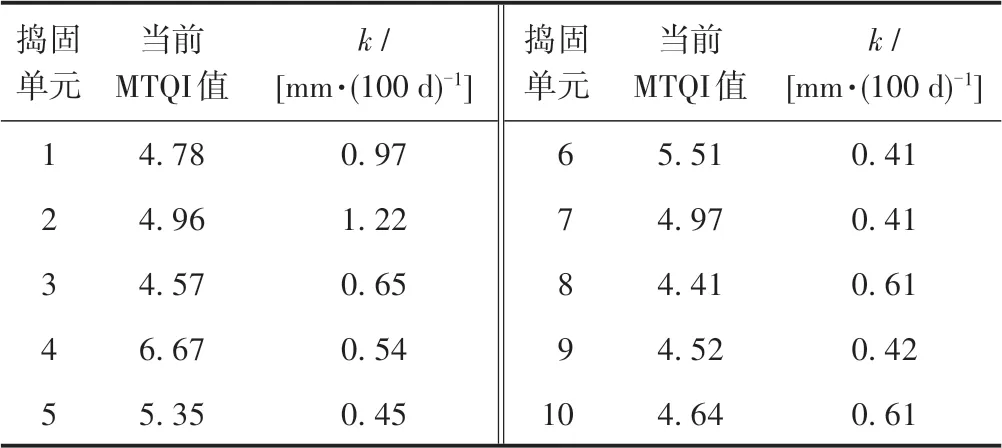
表2 實例各搗固單元百天變化率
據調研,模式1 和模式2 的維修費用分別約為0.5 萬元/km 和1.0 萬元/km。至此,式(9)中各參數取值均已確定,見表3。

表3 實例各參數取值
對于各搗固單元,根據式(9),將表2 和表3 中的數據分別代入進行計算,得到α的計算結果,見圖3。可知,該區段內各搗固單元在模式1和模式2下的Mmax分別為9和10。
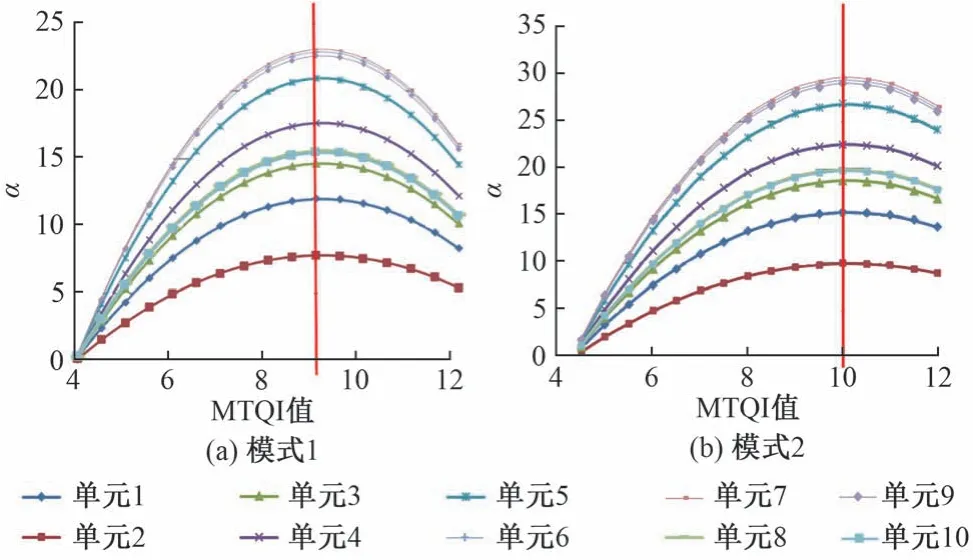
圖3 兩種搗固模式下各搗固單元的α計算結果
各搗固單元下次搗固作業的最佳時間計算公式為
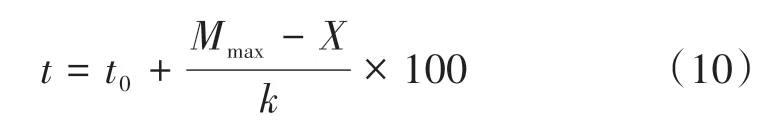
式中:t為下次搗固作業的最佳時間;t0為當前檢測時間;X為搗固單元當前MTQI值。
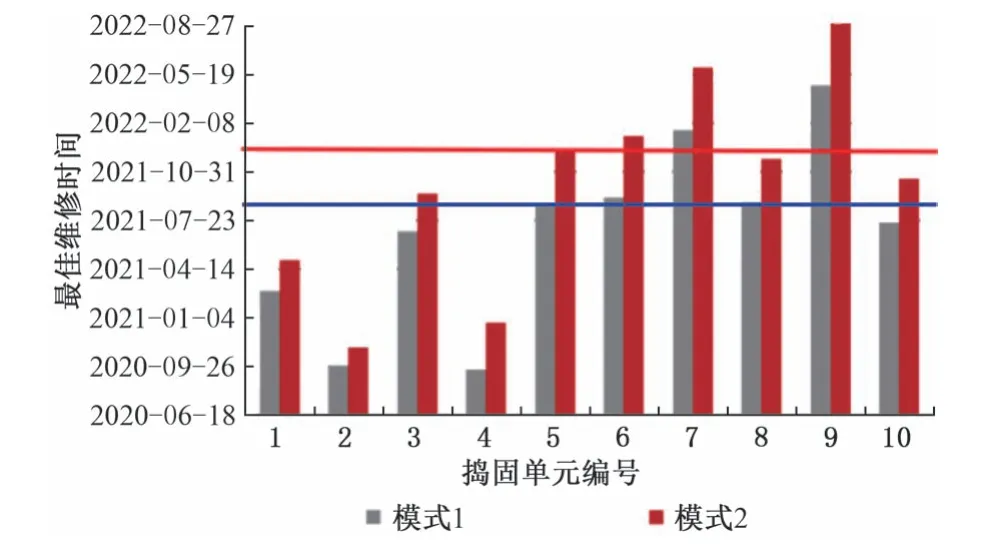
圖4 兩種模式的最佳搗固時機
對于單個2 km 搗固單元安排大機維修不符合我國鐵路工務維修實際,因此按照60%搗固單元超過Mmax須進行大機搗固維修的原則進行區段維修計劃安排。對于以上兩種維修模式,該重載鐵路重車線K250—K270 區段采用模式1 的最佳搗固時機為2021年8月,采用模式2 的最佳搗固時機為2021年12月,見圖4。工務部門可以此為參考,根據線路實際情況,對超過最佳搗固閾值的搗固單元比例進行控制,以確定區段的搗固維修計劃。
由圖3 和圖4 可知,各搗固單元模式2 的αmax均大于模式1,表明模式2使搗固效果和維修費用達到了更好的平衡,且模式2 的搗固周期更長,表明運用模式2進行大機搗固作業,線路質量保期更長。因此,對于所選區段,模式2 比模式1 具有更強的經濟性優勢,采用模式2 進行大機搗固作業,提高線路質量和降低維修成本之間能夠達到更好的平衡。
5 結語
為了在提高線路質量的同時降低維修成本,以二者的比值作為綜合評價指數α,并將α表示為搗固前MTQI 值的函數。通過不同搗固模式的軌道質量恢復模型和搗固周期線性預測方法,求解不同搗固維修模式下使α為最大值時的MTQI 值,即為最佳搗固閾值。利用線性預測方法計算線路惡化至最佳搗固閾值的時間,確定不同維修模式的最佳搗固時機。
以某重載線路區段為例,介紹了最佳搗固時機的計算和應用,計算并對比了單插不穩定/人工測量/09-32型車和單插+單插不穩定/人工測量/09-32型車兩種模式下的最佳搗固閾值和搗固時機。結果表明,單插+單插不穩定/人工測量/09-32 型車模式下線路質量保持時間更長,搗固效果和維修費用能夠達到更好的平衡。

