內殼層電子對過渡金屬鐵熔化溫度的影響

陳春彩

(閩南理工學院 大學物理教研室，福建 石獅 362700 )

過渡金屬鐵在第4周期第Ⅷ族，是地核的主要組成成分.因其化學性質比較活潑，能以多種同素異形體存在于自然界中.鐵有多種晶體結構，常溫常壓下為體心立方BCC-α相結構，當溫度升高到1200K時從BCC-α相過渡到面心立方結構FCC-γ相，而隨著壓強的增大則呈現六角密排結構HCP-ε相，低壓高溫下卻是體心立方結構BCC-δ相等.理論和實驗皆證實了以上幾種晶體結構在鐵的相圖中能夠穩定存在.但在極端高溫高壓條件下，鐵的相圖還留著一些不確定性，其高壓熔化曲線還有最少2000K以上的不明區域[1].熔化是固體發生相變的一種現象，長期以來從事理論和實驗研究工作的學者們對過渡金屬鐵的結構與相變的研究從未間斷過，并得到了許多有價值的結論[1-10].盧志鵬等人用平面波贗勢法研究了鐵從BCC到HCP結構相變，認為鐵磁性的猝滅將促使BCC結構變得不穩定而越過相變勢壘向HCP結構轉變[6].孫博等人用平面波贗勢法研究了過渡金屬鐵的自旋極化總能，認為壓強增加到約140 GPa時，3p電子對自旋極化總能的貢獻將不能忽略[10].鄭傳慶等人用平面波贗勢法計算過渡金屬銅的自旋極化總能，通過劃分不同壓強下銅原子芯態和價態的關系，認為當壓強增加到約139.3 GPa時，3p電子對總能的貢獻將不能忽略，需將其作為價電子處理[11].

元素周期表中過渡金屬鐵的外層電子排布為1s22s22p63s23p63d64s2，最外層電子排布是3d64s2.通常情況下贗勢法是把1s22s22p63s23p6當作內核，把3d64s2作為外殼層價電子.由于特殊的d電子軌道，決定了過渡金屬鐵大多數的物理化學性質.但是隨著壓力的遞增，內層電子的影響將越來越明顯.雖然第一性原理的全電子計算可以將內層電子的貢獻包含在內，但計算量非常大.利用從頭算的密度泛函理論平面波贗勢法，能夠計算過渡金屬的晶格結構與能量的關系，是得到過渡金屬相變熔化溫度的靜力學方法.該方法與全電子計算方法相比，計算量小、相對簡單、能夠直接描述固-液、固-固相變機理的細節.

本文基于從頭算的密度泛函理論及其微擾理論，利用abinit軟件包優化過渡金屬Fe的能量與晶格結構的關系.研究過程中發現：計算過渡金屬鐵的熔化溫度時應把3s23p6這8個電子看作外殼層價電子.

1 計算方法

利用從頭算的密度泛函理論(DFT)及其微擾理論(DFPT)，使用程序包abinit[12]，采用廣義梯度近似(GGA)，Perdew-Burke-Ernzerhof(PBE)泛函[13]和Troullier-Martins(TM)贗勢完成相應的第一性原理計算.為了證實3s23p6這8個電子作為外殼層價電子對計算的影響.計算中統一采用BCC-α相鐵作為研究對象.采用了統一的參數如表1所示，其中E-cut代表平面波的截斷能，K-point指倒格子中對Brillouin區作Monkhorst-Pack抽樣，取6×6×6能保證計算時能量可以收斂.smearing指E-cut的平滑拖尾參數，dilatmx是晶格參數的最大縮放比，spint指初始自旋極化參數，nband是能帶數.

表1 優化參數

2 分析與討論

2.1 3d64s2作最外層價電子

過渡金屬鐵在常溫常壓下是BCC結構.其外層電子排布為1s22s22p63s23p63d64s2，最外層電子排布是3d64s2.利用GGA-PBE(1996)[13]及TM贗勢法，優化計算得到α-Fe磁矩為M=3.27μB，最優晶胞參數為a=0.311 388 nm，比實驗測量結果a=0.286 64 nm[13]偏大8.6%.

令晶格參數[10]a=b=c，α=β=γ=90°.原胞的3個基矢分別為(x,0.5,0.5)，(0.5,x,0.5)和(0.5,0.5,x).當x=0時對應的是面心立方(FCC)結構，x=-0.25對應的是簡單立方(SC)結構，x=-0.5則是體心立方(BCC)結構.經過優化計算，得到晶格能量E隨原胞參數x的變化關系如圖1所示.由圖1可以看出x=-0.25時，SC結構最不穩定，符合實際；能量最低的位置在x=-0.48處，能量最低說明結構最穩定.根據實驗相圖可知，在常溫常壓下，α-Fe的最穩定結構應是BCC體心立方結構，即當x=-0.5時方為能量最低.顯然計算結果和實驗不符合.

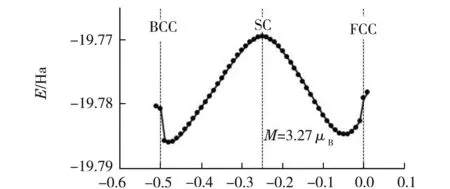
x圖1 α-Fe晶格能量與原胞參數x的變化關系

考慮是交換關聯能近似函數選擇不恰當引起的.按交換關聯函數不同分為LDA(local density approximation，局域密度近似)和GGA(generalized-gradient approximation，廣義梯度近似).局域密度近似一般應用于電子密度變化相對平緩的系統，對于一些強關聯體系如過渡金屬、稀土金屬等缺點是比較明顯的.先入為主地選擇了GGA進行優化計算.但是為了排除交換關聯近似的影響，采用LDA和TM贗勢(統一的參數如表1中的外層是8個電子情況所示)對α-Fe進行優化計算.

優化后得到常溫常壓過渡金屬α-Fe磁矩為M=2.02μB，最優晶胞參數為a=0.280 14 nm，比實驗測量結果a=0.286 64 nm[14]偏小2.3%.通過對晶胞參數的比較，顯然LDA的計算結果略微優于GGA的計算結果.優化得到的晶格能量E隨原胞參數x的變化關系如圖2所示.由圖2可知，x=-0.25時，SC結構最不穩定，符合實際.x=0時，FCC結構最穩定，這與常壓下BCC結構能穩定存在的事實不符.由此，比較得出LDA比GGA更不適合用于過渡金屬α-Fe熔化溫度的計算.最后我們猜想有可能是在選擇贗勢的時候沒有考慮內殼層3s23p6這8個電子對外層價電子的影響.

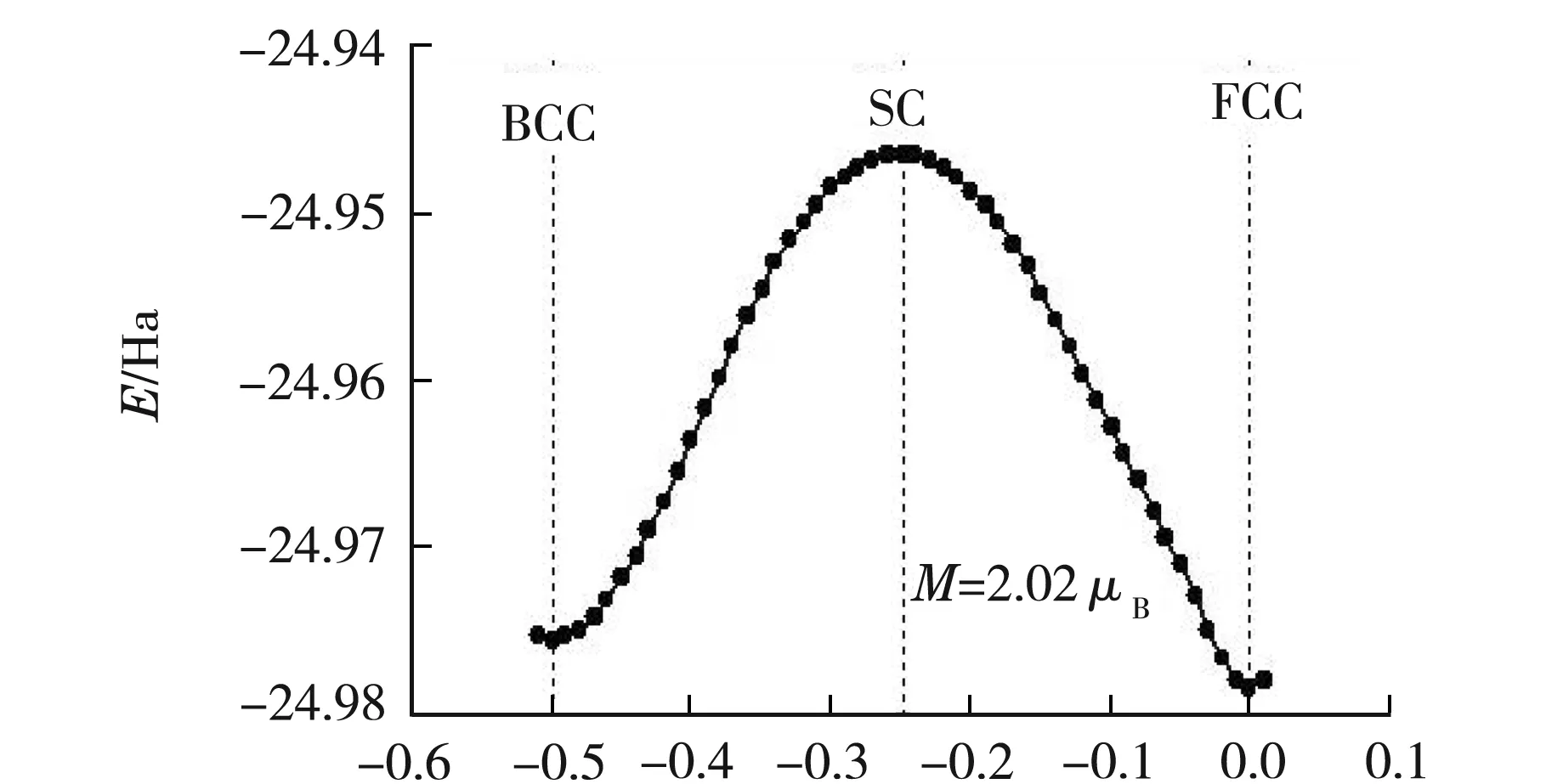
x圖2 α-Fe晶格能量與原胞參數x的變化關系

2.2 3s23p63d64s2作最外層價電子

在考慮第3殼層3s23p6的8個電子對外殼層3d64s2電子的影響后，對 TM贗勢做了適當修改.把3s23p63d64s2作為外殼層，內核只留1s22s22p6.采用GGA-PBE(1996)和修改后的TM贗勢，按表1的參數再次對過渡金屬α-Fe在常溫常壓下進行優化計算.

優化后得到常溫常壓過渡金屬α-Fe磁矩為M=2.86μB，最優晶胞參數為a=0.297 83 nm.比Torrent等人[15]用投影平面波(PAW)方法計算得到的a=0.284 nm偏大4.9%，比實驗測量結果a=0.286 64 nm[14]偏大3.9%.優化得到的晶格能量E隨原胞參數x的變化關系如圖3所示.容易看出x=-0.25時E=-115.622 697 6 Hatree，即SC結構最不穩定，符合實際.當x=-0.5時，E=-115.640 308 5 Hatree，即BCC結構最穩定，這與常壓下BCC結構能穩定存在的實際相符.比較得出SC結構的能量比BCC結構的能量高出值ΔE=0.017 610 9 Hatree=46.24 KJ/mol.把這個能量差化成溫度等于1 853 K.而1 853 K與常溫常壓下α-Fe的熔化溫度1 811 K[14]相差2.3%，可以說是非常接近的.這與熱力學理論中漲落的持續變化將引起體系發生相變的觀點相符合.

x圖3 α-Fe晶格能量與原胞參數x的變化關系

3 結 論

本文采用從頭算的密度泛函理論及其微擾學說，使用abinit軟件包平面波贗勢法討論過渡金屬Fe的晶格結構與能量的關系.計算結果表明在選取TM贗勢時必須考慮內殼層3s23p6這8個電子對外層價電子的影響.優化得到的晶格能量E隨原胞參數x曲線符合實際，得到的熔化溫度與實驗結果吻合較好.認為計算過渡金屬Fe的熔化溫度時應考慮內殼層價電子3s23p6對外殼層價電子的影響作用.