基于逸度與壓力計算頁巖吸附甲烷的等量吸附熱差異分析
——以延長探區延長組頁巖為例

2021-04-08 02:32:16張麗霞梁全勝

巖性油氣藏 2021年2期

薛培，張麗霞，梁全勝，師毅

（1.西北政法大學，西安 710063；2.陜西延長石油（集團）有限責任公司研究院，西安 710075；3.延長石油集團油氣勘探公司，陜西延安 716000）

0 引言

頁巖氣的主要賦存空間為頁巖中發育的微納米級孔隙，其賦存狀態具有吸附態、游離態和溶解態等3 種形式，以吸附態和游離態為主，其中吸附氣占比可達20%～85%［1］。由于吸附過程中，存在著氣體分子動能及勢能的變化，因此頁巖氣的吸附過程為放熱。分析吸附過程的熱力學特征有助于深入認識頁巖氣的吸附機理。

現有的頁巖氣及煤層氣吸附熱力學特征分析普遍采用基于Clasius-Clayperon 方程的吸附等量線標繪法來計算等量吸附熱［2］，區別在于等量吸附熱計算所用的等溫吸附數據類型存在差異。文獻［3-10］采用基于壓力的等溫吸附數據作為等量吸附熱計算的基礎數據，而文獻［11-15］采用基于逸度的等溫吸附數據計算等量吸附熱。由于經典的Clasius-Clayperon 方程是在假設吸附氣為理想氣體并忽略吸附相體積的基礎上推導而來［16］，然而頁巖和煤等溫吸附CH4過程的溫度和壓力范圍均已超過CH4的臨界點（CH4的臨界溫度為-82.6 ℃，臨界壓力為4.64 MPa），等溫吸附過程屬于超臨界吸附的范疇［17］，因此經典的Clasius-Clayperon 方程并不適用于頁巖與煤的吸附熱力學特征分析，對于非理想氣體的吸附熱力學分析，需將Clasius-Clayperon 方程中的壓力替換為逸度［18］。目前尚未見到關于逸度與壓力的選擇對等量吸附熱計算結果影響的量化評價。

筆者以延長探區甘泉地區延長組頁巖為研究對象，開展不同溫度下（30～70 ℃）頁巖吸附CH4的等溫吸附實驗及絕對吸附量的校正，對比分析逸度與壓力之間的差異，以及基于逸度-絕對吸附量和壓力-絕對吸附量獲得的等量吸附熱的差異，以期完善頁巖等量吸附熱的計算方法，進而明確陸相頁巖吸附熱力學特征。

1 頁巖等溫吸附實驗

1.1 實驗樣品與方法

等溫吸附實驗樣品來自延長探區甘泉地區延長組長7 段黑色頁巖。實驗樣品地球化學分析表明，該樣品總有機碳（TOC）質量分數為5.32%，有機質類型為Ⅱ1型，有機質成熟度（Ro）為0.97%。礦物組成分析表明，該樣品黏土礦物含量較高，質量分數為52.4%，石英質量分數為24.5%，長石質量分數為14.1%，并含有少量的黃鐵礦和菱鐵礦［19］。

等溫吸附實驗共設定30 ℃，40 ℃，50 ℃，60 ℃，70℃等5 個溫度點，實驗壓力為0.4～11.0 MPa，單個壓力點下的吸附平衡時間不少于12 h，采用純度99.99%的甲烷為吸附氣。樣品預處理及實驗操作規范參照了GB/T 19560—2008的相關規定［20］。

1.2 過剩吸附量與絕對吸附量

延長組頁巖樣品等溫吸附曲線如圖1 所示。由于過剩吸附量表征了實際吸附相密度減去氣相密度所剩部分的吸附量，過剩吸附量小于絕對吸附量。同時采用過剩吸附量計算獲得的等量吸附熱及初始等量吸附熱小于采用絕對吸附量獲得的等量及初始等量吸附熱。因此需要將過剩吸附量校正為絕對吸附量，采用絕對吸附量計算等量吸附熱。

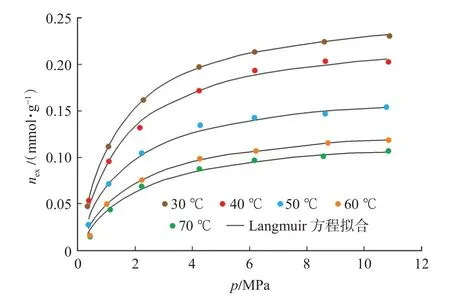
圖1 延長組頁巖等溫吸附曲線Fig.1 Adsorption isotherm of shale of Yanchang Formation

根據Gibbs 吸附量的定義，過剩吸附量與絕對吸附量間的關系［21］為

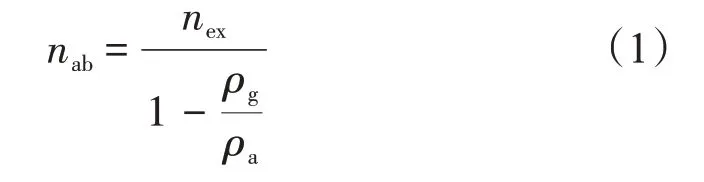
式中：nab為絕對吸附量，mmol/g；nex為過剩吸附量，mmol/g；ρg為氣相密度，g/cm3；ρa為吸附相密度，g/cm3。

采用真實氣體狀態方程計算氣相密度，氣相密度可表示為

式中：M為摩爾質量，g/mol；R 為通用氣體常數，8.314 J/（K·mol）；Z為真實氣體壓縮因子；T為絕對溫度，K；P為氣體壓力，MPa。

本文采用Peng-Robinson 方程［22］計算壓縮因子。P-R（Peng-Robinson）方程表示為壓縮因子Z的形式為

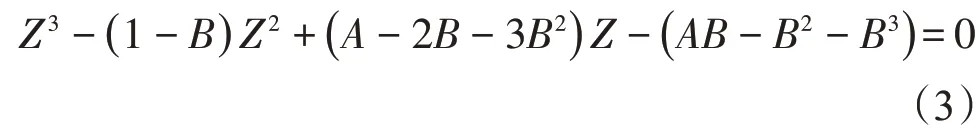
參數A和B的計算方法為

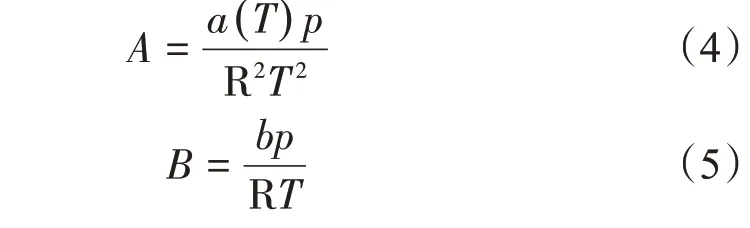
式（4）、式（5）中a(T)為內聚力參數，可表示為

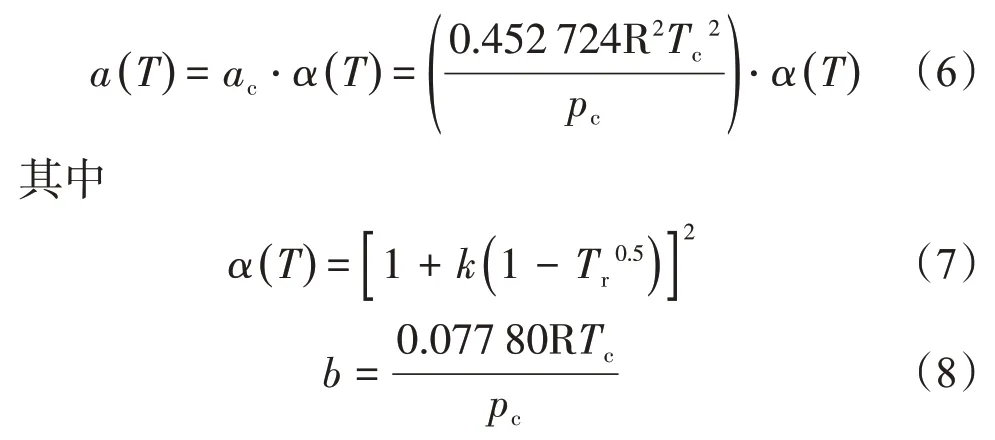
式中：Tc為臨界溫度，K；p為壓力，Pa；pc為臨界壓力，Pa；α()T為與對比溫度Tr和偏心因子ω有關的函數；b為協體積項；Tr為對比溫度，Tr=T/Tc；k為與偏心因子ω有關的函數。

不同的ω取值范圍內，k表達式不同，當偏心因子取值為0 ＜ω＜0.5 時，k可表示為

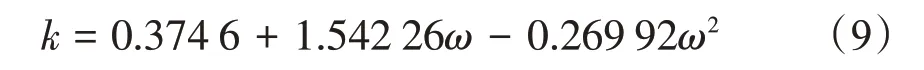
式中：ω為偏心因子，CH4的偏心因子取值0.008。

經計算，得出在溫度為30～70 ℃、壓力為0～15 MPa 時甲烷的氣相密度（圖2）。

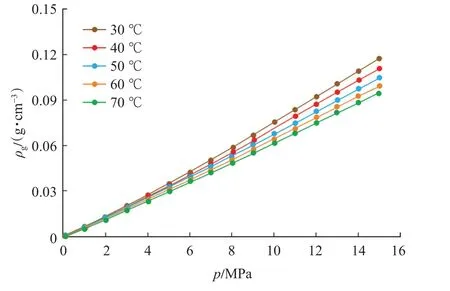
圖2 甲烷的密度曲線Fig.2 Density curve of CH4

由于Ozawa 等［23］經驗公式法適用于較寬溫壓范圍內的吸附相密度計算［19］，因此本文采用Ozawa經驗公式法計算吸附相密度，其計算公式為

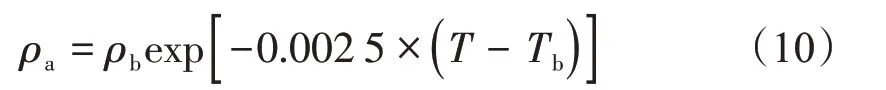
式中：ρb表示沸點密度，g/cm3（CH4的沸點密度為0.424 g/cm3）；Tb表示沸點，K（CH4的沸點為111.65 K，即-161.5℃）。

經計算，得出在溫度為30～70 ℃時CH4的吸附相密度（圖3）。

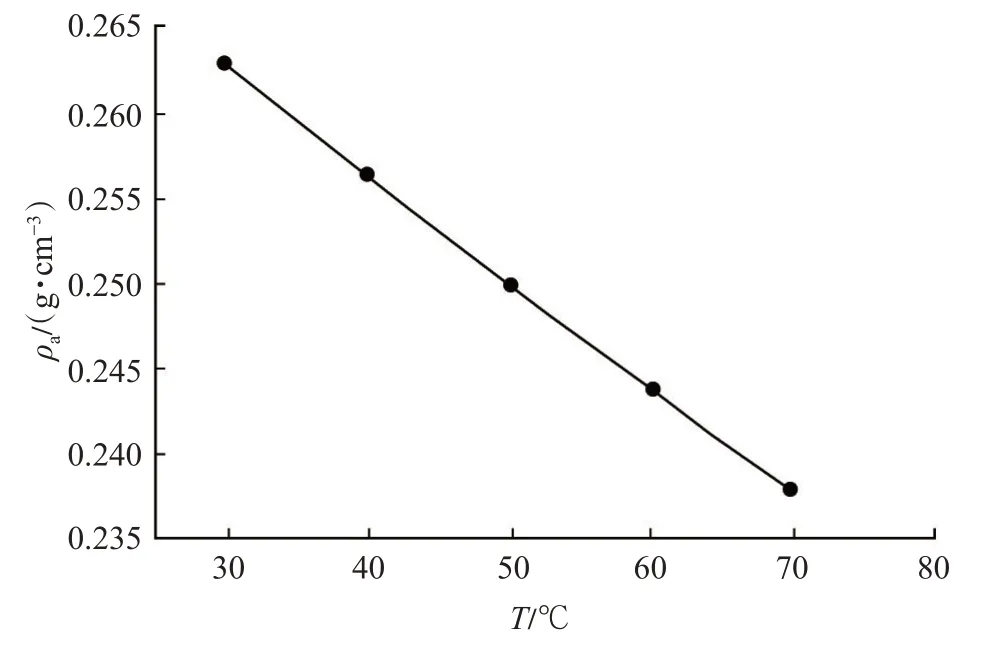
圖3 甲烷的吸附相密度曲線Fig.3 Adsorbed phase density curve of CH4

基于式（1），結合CH4的氣相密度（圖2）和吸附相密度（圖3），即可實現由過剩吸附量（圖1）向絕對吸附量的校正，校正后的絕對吸附量曲線如圖4所示。采用Langmuir 方程對絕對吸附量曲線進行了擬合，擬合相關系數在0.98 以上，Langmuir 方程擬合參數如表1 所列。表1 中VL-p，PL-p分別表示壓力-絕對吸附量數據的Langmuir 方程擬合參數。

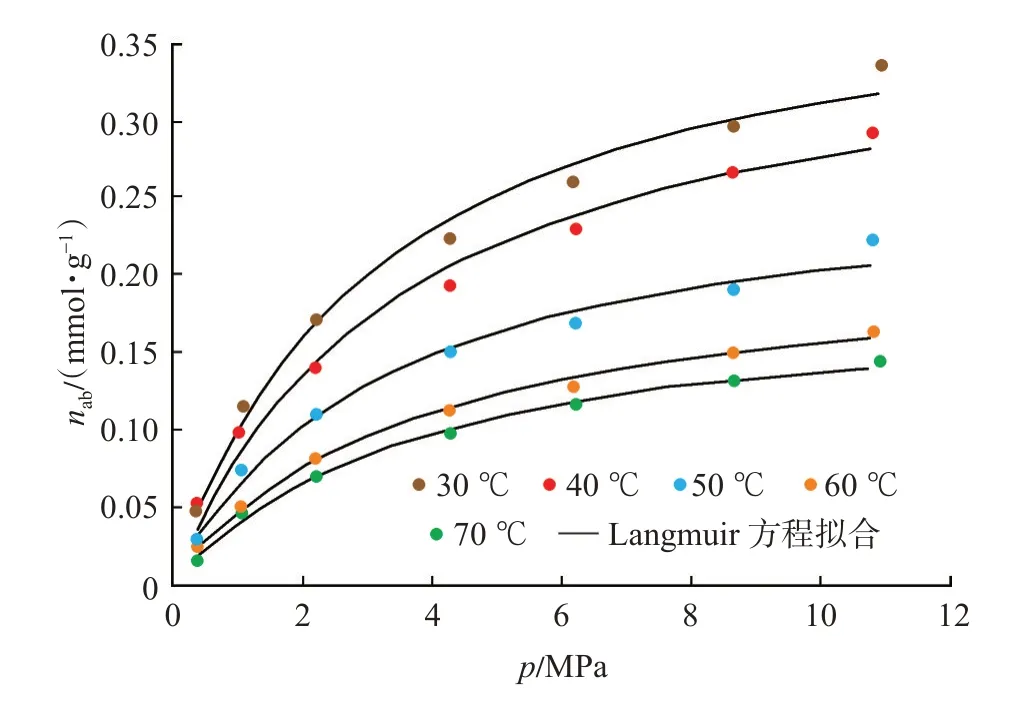
圖4 絕對吸附量曲線Fig.4 Absolute adsorption isotherm curves

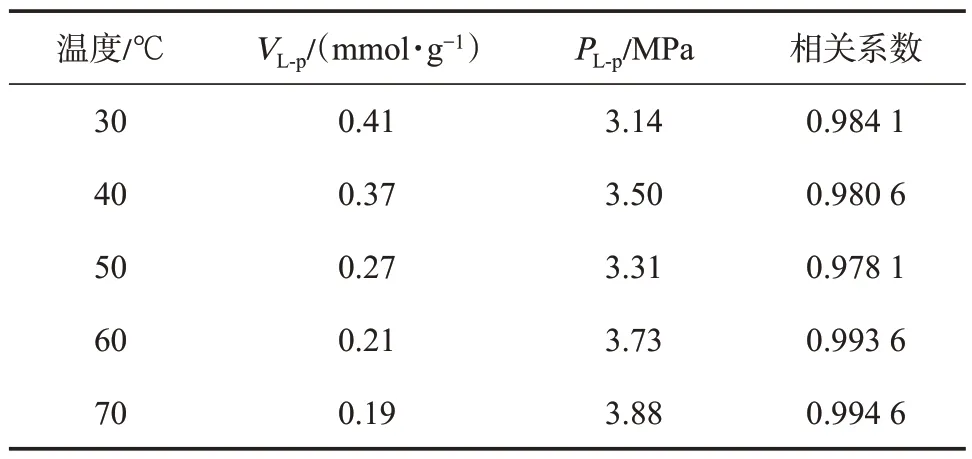
表1 壓力-絕對吸附量曲線的Langmuir 方程擬合參數Table 1 Fitting parameters of Langmuir equations for the pressure-absolute adsorption isotherm

2 逸度

2.1 逸度的定義及計算方法

逸度及逸度系數是變組成體系熱力學計算中的重要基本概念，也是相平衡和化學反應平衡研究的重要工具［24］。逸度是在處理非理想氣體化學勢時引入的概念。對于1 mol 的純物質的熱力學關系式［25］為

式中：μ為化學勢，J/mol；Vm為摩爾體積，m3/mol。

對于理想氣體，其狀態方程為pVm=RT，則

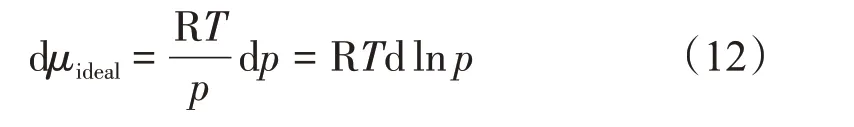
對于真實氣體，其狀態方程為pVm=ZRT，則

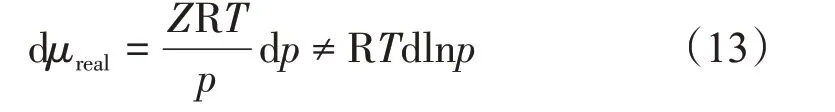
據文獻［25］報道，1901 年，Lewis 提出將理想氣體與真實氣體的偏差放到壓力項做一次性修正，并定義新函數，使得

式中：f為逸度，Pa。對于理想氣體，其逸度等于壓力；對于真實氣體，可把逸度看作校正的壓力，也表征體系的逃逸趨勢。

同時定義逸度系數為

逸度系數可用來衡量真實氣體偏離理想狀態的程度，φ越接近1，則氣體越接近理想氣體。純組分的逸度和逸度系數可采用狀態方程法、圖解法、對比狀態法和近似法計算［26］。本文采用P-R 狀態方程計算CH4的逸度，其逸度系數［18］可表示為

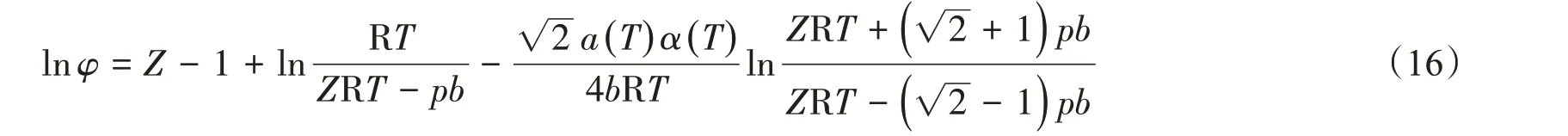
2.2 逸度與逸度系數

利用式（16）及P-R 方程即可得出逸度及逸度系數。當實驗溫度為30 ℃，40 ℃，50 ℃，60 ℃，70 ℃，壓力為0.36～11.00 MPa 時的逸度及逸度系數曲線如圖5 所示。

從圖5（a）可看出，在低壓力區間（0.36～2.21 MPa）內，逸度與壓力基本相等，隨著壓力的增加，逸度與壓力的差距逐漸增大。為了清晰地呈現二者的差異與溫度和壓力的關系，繪制了不同溫度下壓力與逸度差值隨壓力的變化曲線［圖5（b）］。從圖5（b）可看出，當壓力大于逸度，特別是在低溫高壓條件下，壓力與逸度的差值越發明顯。具體而言，低壓力階段（0.36～2.21 MPa），壓力與逸度的差值較小；處于0.002～0.010 MPa 時，溫度對二者差值的影響較小；隨著壓力的升高，二者的差值逐漸增加，以30℃為例，壓力為0.36 MPa 時，差值為0.002 MPa，當壓力升高至11 MPa 時，差值增加至2.10 MPa；同時隨著壓力的升高，溫度對差值的影響越發明顯，溫度越低，二者的差值越大，例如當壓力為11 MPa，溫度為30 ℃，40 ℃，50 ℃，60 ℃，70 ℃時，二者的差值分別為2.01 MPa，1.78 MPa，1.59 MPa，1.43 MPa，1.28 MPa。

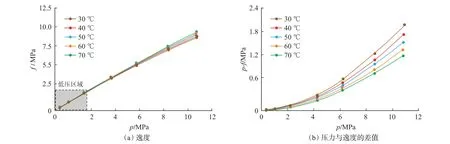
圖5 逸度及壓力與逸度的差值曲線Fig.5 Fugacity and difference curve of pressure and fugacity

此外，逸度系數也反映了壓力與逸度的差別。由于逸度系數定義為φ=f/p，且受限于不同溫壓條件下逸度與壓力的關系，逸度系數小于1。隨著壓力的升高，逸度系數逐漸降低，同時，低溫條件下的逸度系數隨壓力增加所表現出的下降速率要大于高溫條件下的下降速率（圖6）。

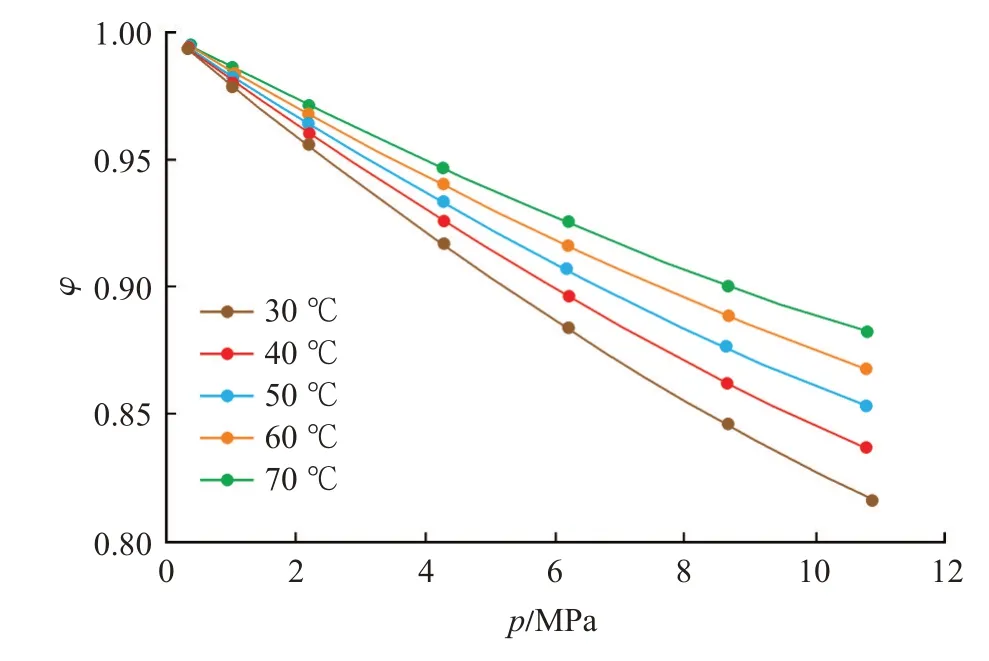
圖6 逸度系數曲線Fig.6 Fugacity coefficient curve

文中采用逸度-絕對吸附量數據作為等量吸附熱計算的基礎數據，因此需要將圖4 中以壓力作為橫坐標的等溫吸附曲線轉換為以逸度作為橫坐標的等溫吸附曲線，以此作為熱力學分析的基礎數據（圖7）。由于低壓力階段，壓力與逸度差值較小，而隨著壓力的增加，二者差值增大。因此，圖7 所示的逸度-絕對吸附量曲線在高壓部分數據點相對于壓力-絕對吸附量曲線會向左平移，橫坐標平移距離即為壓力與逸度的差值，曲線形態相較于圖4 所示的壓力-絕對吸附量曲線發生改變。若將Langmuir方程中的參數p用逸度f替換，方程形式保持不變，對逸度-絕對吸附量數據進行了擬合。擬合結果表明，方程擬合相關系數均在0.98 以上。由于在相同的溫度和壓力條件下，逸度小于壓力，且隨著壓力的升高，二者差值增大，因此相對于圖4 而言，逸度-絕對吸附量的Langmuir 方程的擬合參數Langmuir體積（VL-f）及Langmuir 壓力（PL-f）均略大于壓力-絕對吸附量的擬合結果（表1、表2）。

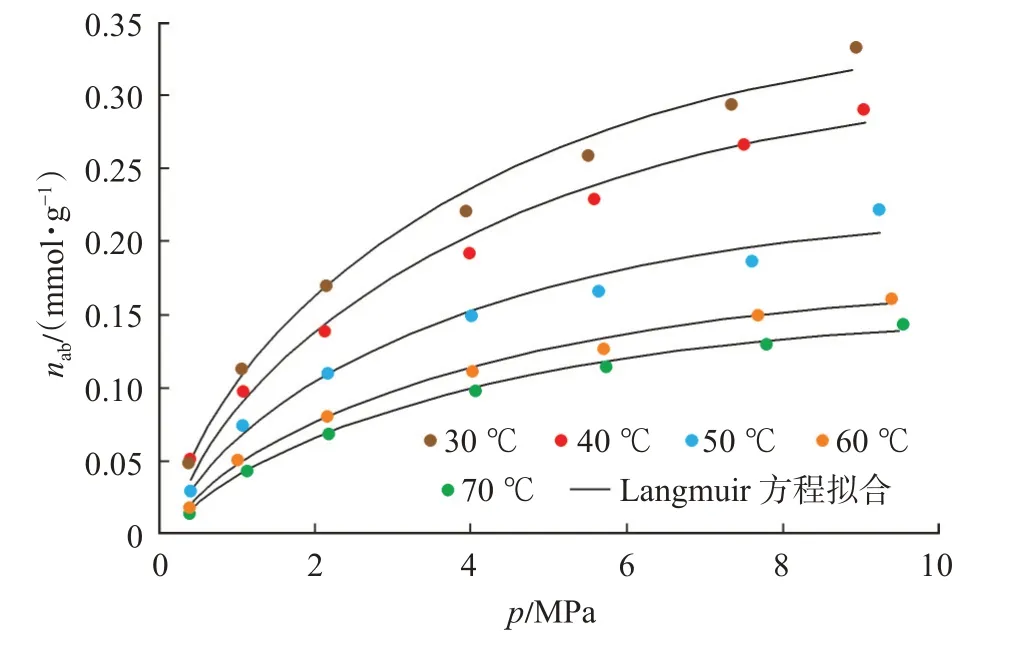
圖7 基于逸度的絕對吸附量曲線Fig.7 Absolute adsorption curve based on fugacity

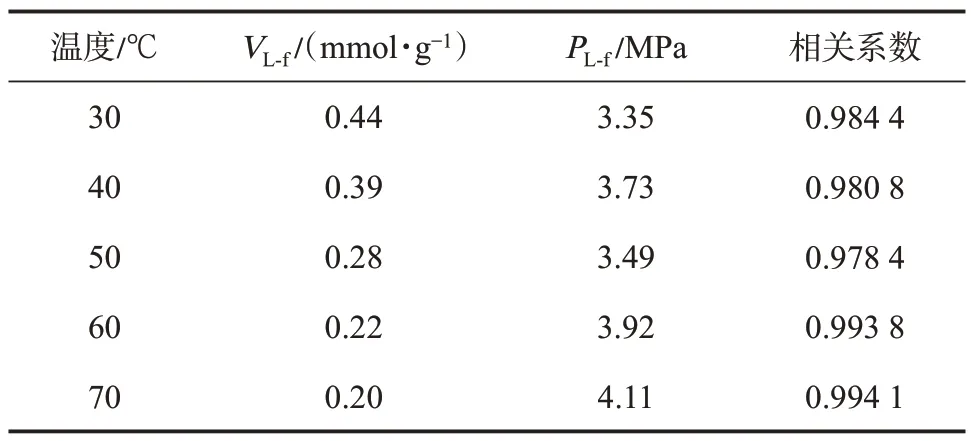
表2 逸度-絕對吸附量曲線的Langmuir 方程擬合參數Table 2 Fitting parameters of Langmuir equations for fugacity-absolute adsorption isotherm

3 等量吸附熱

3.1 等量吸附熱的計算方法

等量吸附熱（qst）是指當壓力（p）、溫度（T）及吸附劑表面積（A）恒定時，吸附劑表面吸附無限小量的吸附質，吸附體系所釋放的熱量，其數學表達式［27］為

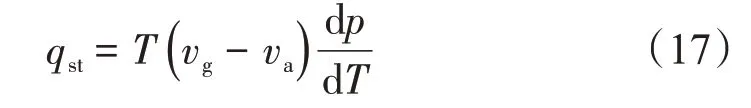
式中：qst為等量吸附熱，kJ/mol；vg為體相氣體的摩爾體積，m3/mol；va為吸附相氣體的摩爾體積，m3/mol。

若忽略吸附相體積，且視體相氣體為理想氣體，則式（17）可寫作經典的Clasius-Clayperon 方程［10］，即

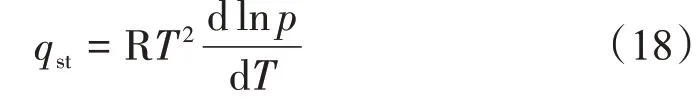
由于頁巖及煤巖等溫吸附CH4實驗的溫度和壓力范圍大多分別集中在20～80 ℃及0～20 MPa［28-29］，同時CH4的臨界溫度為-82.6 ℃，臨界壓力為4.64 MPa，在此溫度和壓力范圍內的等溫吸附過程存在著由氣相吸附向超臨界流體吸附的轉變，氣體分子行為已不再滿足理想氣體假設。以CH4壓縮因子為例（圖8），不同溫度下CH4的壓縮因子隨壓力的增加，先減小后增加，偏離了理想氣體狀態。因此針對非理想氣體的熱力學分析，若采用Clasius-Clayperon 方程計算等量吸附熱，則需要將壓力p替換為逸度f［18，30-31］，即將式（18）轉變為

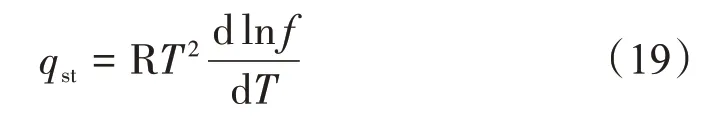
進而采用吸附等量線標繪法計算固-氣吸附體系的等量吸附熱。

基于Clasius-Clayperon 方程的吸附等量線標繪法在等量吸附熱計算中應用較為廣泛［2］。該方法首先需要對式（19）兩端變形并積分可得

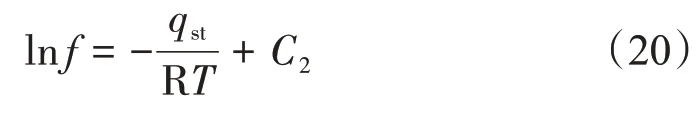
由式（20）可知，逸度的自然對數lnf與絕對溫度的倒數1/T呈線性關系，由斜率得到吸附量n對應的qst。假設斜率為A，則等量吸附熱計算式為

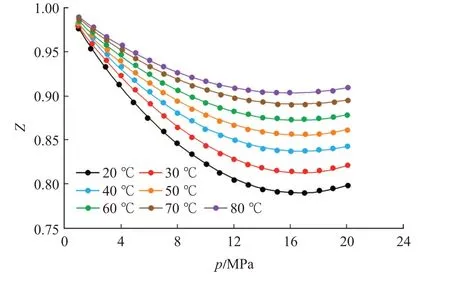
圖8 CH4的壓縮因子（采用P-R 方程計算）Fig.8 Compression factor of CH4by P-R equation

3.2 基于逸度與壓力的等量吸附熱特征對比

筆者分別采用逸度-絕對吸附量和壓力-絕對吸附量數據對頁巖吸附CH4的等量吸附熱進行計算。同時，在后續行文過程中將基于逸度-絕對吸附量數據獲得的等量吸附熱標記為qst-f，相對應地將基于壓力-絕對吸附量數據獲得的等量吸附熱標記為qst-p，以便區分。

首先，依據lnp-nab及lnf-nab的數據特征分別選用線性函數和冪函數對lnp-nab及lnf-nab進行了擬合（圖9）。擬合結果表明，lnp與nab呈明顯的線性關系，lnf與nab呈明顯的冪函數關系，函數擬合相關系數均超過0.99。

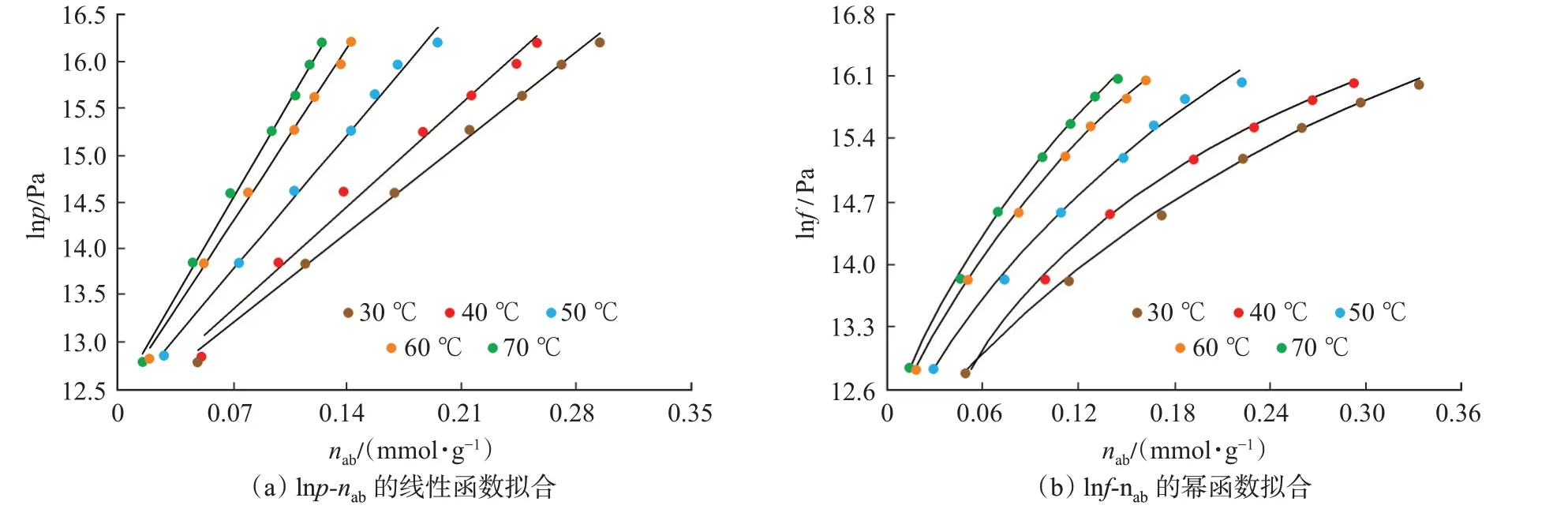
圖9 lnp-nab及lnf-nab數據的函數擬合Fig.9 Fitting curve of lnp-naband lnf-nab

利用擬合得到的lnp-nab與lnf-nab的線性函數、冪函數分別計算不同絕對吸附量下的lnp及lnf，進而繪制不同絕對吸附量下的lnp-1/T 及lnf-1/T曲線，并分別對曲線進行線性函數擬合（圖10），lnp-1/T及lnf-1/T曲線均符合線性相關性，且相關系數均超過0.95。

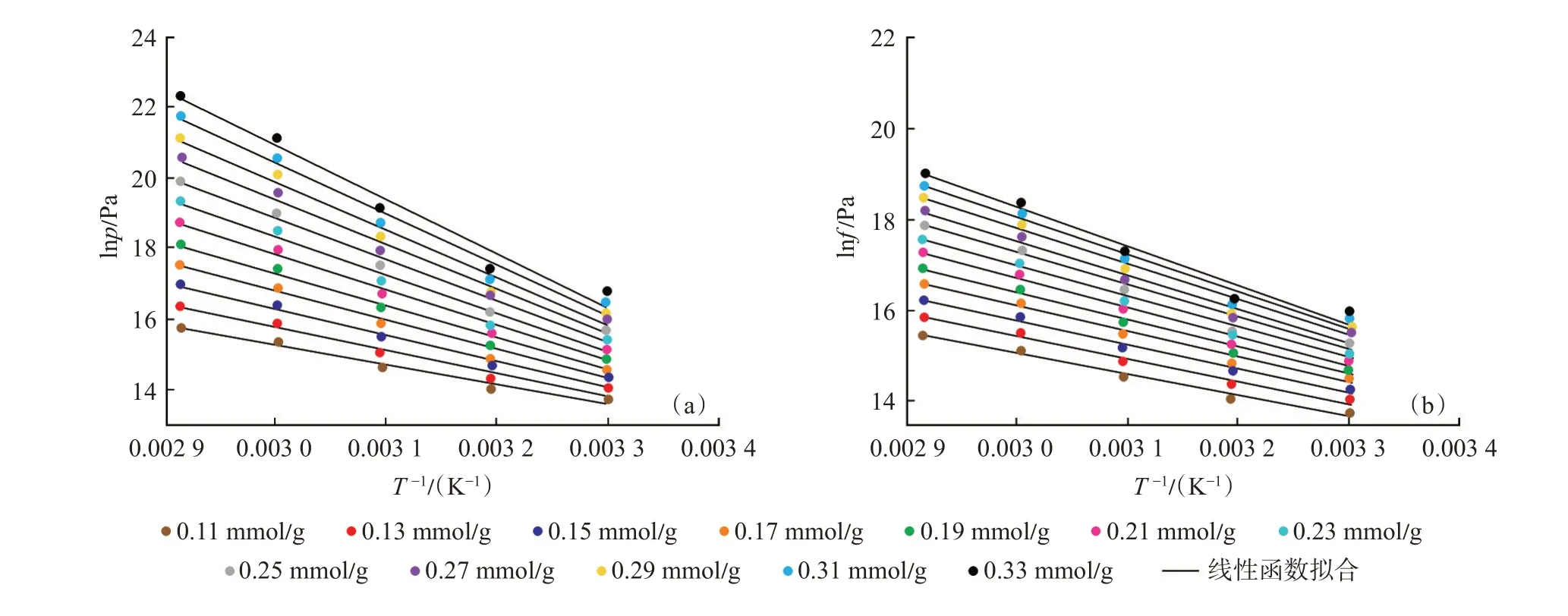
圖10 lnp-1/T（a）及lnf-1/T（b）數據的線性函數擬合Fig.10 Linear fitting curves of lnp-1/T（a）and lnf-1/T（b）

分別利用lnp-1/T［圖10（a）］及lnf-1/T［圖10（b）］曲線線性擬合函數的斜率結合式［式（21）］計算基于壓力-絕對吸附量及逸度-絕對吸附量的等量吸附熱，計算結果如圖11 所示。

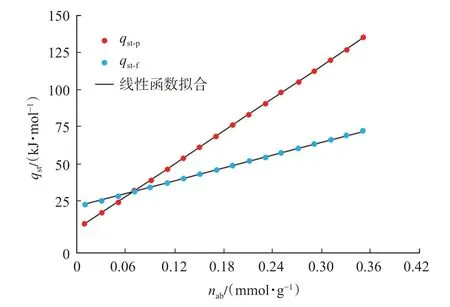
圖11 基于逸度-絕對吸附量及壓力-絕對吸附量獲得的等量吸附熱Fig.11 Isosteric heat of adsorption based on fugacity-ab‐solute adsorption isotherm and pressure-absolute adsorption isotherm

基于逸度的等量吸附熱及基于壓力的等量吸附熱均與絕對吸附量滿足良好的線性關系，相關系數均在0.99 以上（表3），且隨著絕對吸附量的增加，等量吸附熱均逐漸升高（圖11）。絕對吸附量由0.01 mmol/g 上升至0.35 mmol/g 時，基于逸度的等量吸附熱為22.31～72.35 kJ/mol，基于壓力的等量吸附熱為9.59～134.97 kJ/mol。

等量吸附熱的大小與固體表面的強/弱吸附位點分布的均一性及吸附氣分子間作用力有關［32］。吸附過程中，氣體分子會優先在固體表面的強吸附位點吸附，隨著吸附的進行，當強吸附位點吸附逐漸飽和后，氣體分子逐步在弱吸附位點吸附，這造成了等量吸附熱隨著吸附量的增加而降低；同時，隨著吸附量的增加，固體表面的吸附態分子密度增加，吸附氣分子間的作用力增加，這造成了等量吸附熱隨吸附量增加而升高。由此可見，CH4在甘泉地區長7 段泥巖孔隙表面的吸附過程中，吸附質分子間的作用力是存在的，且相對于吸附劑表面的非均一性，前者吸附質分子間的作用力對等量吸附熱的影響是主要的。

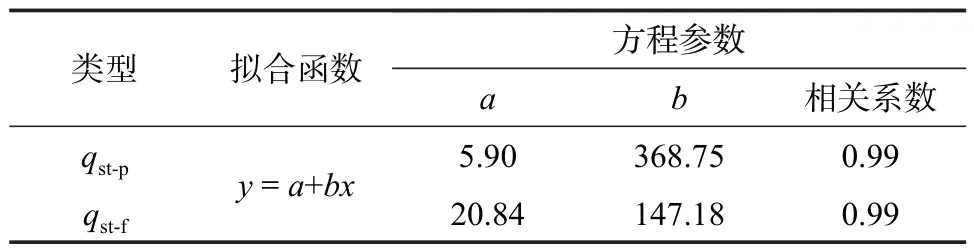
表3 等量吸附熱曲線的線性函數擬合參數Table 3 Linear function fitting parameters of isosteric heat of adsorption

在采用等量吸附線標繪法計算等量吸附時，壓力或逸度的選擇并不會改變等量吸附熱曲線的線性單調性特征，二者均反映了等量吸附熱具有明顯的單調遞增的線性特征。區別在于，基于逸度的等量吸附熱（qst-f）曲線的斜率小于基于壓力的等量吸附熱（qst-p）曲線。由于等量吸附熱隨吸附量增加而上升是受吸附質分子間相互作用的影響，隨著吸附的進行，吸附劑表面吸附位點對吸附質分子的作用力逐漸減弱，等量吸附熱曲線將更多地反映出吸附質分子間作用力的影響。因此可以認為，若采用壓力-絕對吸附量計算等量吸附熱，則會造成等量吸附熱計算結果中吸附質分子間作用力的影響過大。

此外，在絕對吸附量小于0.065 mmol/g時，基于逸度的等量吸附熱（qst-f）大于基于壓力的等量吸附熱（qst-p）；絕對吸附量大于0.065 mmol/g 時，前者（qst-f）小于后者（qst-p）；二者在絕對吸附量為0.065 mmol/g處曲線相交。為定量評價逸度與壓力在等量吸附熱計算結果中的誤差，引入相對誤差（δ）的概念，即

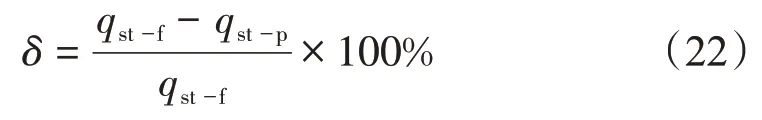
經計算，絕對吸附量為0.01～0.35 mmol/g 時，相對誤差為-86.54%～57.01%（圖12），若以±5%作為合理的相對偏差范圍，那么僅在絕對吸附量為0.060～0.074 mmol/g 時，相對偏差處于合理范圍。特別在低吸附量，即低壓力階段，基于逸度與壓力的等量吸附熱仍然具有較高的誤差。例如，當低吸附量為nab=0.01 mmol/g 時，相對偏差高達52%。其原因在于，雖然在低壓力條件下，壓力與逸度的差值較小，但在高壓力階段，逸度與壓力的差值較大，致使高壓階段中逸度-絕對吸附量曲線的形態與壓力-絕地吸附量曲線存在較大的差異，進而影響到吸附等量線標繪法計算過程中lnp-nab與lnf-nab曲線的擬合函數發生改變，因此在低壓階段，基于壓力與逸度的等量吸附熱曲線出現了較高的相對偏差。由此可見，采用壓力-絕對吸附量作為計算等量吸附熱的基礎數據，會造成較大的誤差。