考慮變形滯后效應的高液限土路基模量反算方法

劉闖　張銳　滕煜晟　任天锃　楊博

摘 要：為了提高便攜式落錘彎沉儀（PFWD）測定高液限土路基回彈模量的精度，考慮變形滯后效應對反算結果的影響，提出了一種基于Kelvin粘彈性模型和準靜態動力分析反算模量的方法。通過現場試驗，驗證了新方法的有效性。研究結果表明：利用高液限土填筑的下路堤模量較低，在PFWD沖擊荷載作用下，其頂面豎向位移峰值明顯滯后于荷載峰值，且荷載位移曲線非線性顯著;基于線彈性模型的常規反算方法使得反算模量遠大于實測模量，平均相對誤差為52.5%;新方法能較好地反映沖擊荷載作用下變形滯后特征，反算相對誤差僅為9.2%。隨著路基模量增大，路基變形滯后效應不顯著，常規方法和新方法反算結果相近，但新方法反算結果的精度更高。

關鍵詞：道路工程;粘彈性模型;準靜態;模量反算;變形滯后;高液限土

中圖分類號：U416.1;TU433? ?文獻標志碼：A ??文章編號：2096-6717（2021）02-0068-08

Abstract： In order to improve the accuracy of Portable Falling Weight Deflectometer （PFWD） in measuring the resilient modulus of high liquid limit soil subgrade， the influence of deformation lags effect on the back-calculation result was considered and a new method for back-calculation of? the modulus was proposed based on Kelvin viscoelastic model and quasi-static dynamic analysis method. The effectiveness of the new method is verified by field tests. The results show that the measured modulus of the lower embankment filled with high liquid limit soil is lower and the peak vertical displacement of the top surface of the embankment obviously lags behind the peak value of the load under the impact load of PFWD. Furthermore， the load-displacement curve is significantly nonlinear. In addition， the conventional method based on linear elastic model makes the back-calculated modulus much larger than the measured modulus. The average relative error between back-calculated and the measured modulus reaches up to 52.5%. However， the new method can better reflect the deformation lag characteristics under impact load. The average relative error between them is only 9.2%. With increase of subgrade modulus， the lag effect of the deformation is not significant. The back-calculating results via conventional and new methods are similar， but the accuracy of the new method is higher.

Keywords：road engineering; viscoelastic model; quasi-static; modulus back-calculation; deformation lag; high liquid limit soil

高液限土在中國南方地區分布廣泛，天然含水率高，水穩性差，用于公路路基填筑時，通常用作下路堤填料，并在濕法重型擊實標準控制下壓實。由于高液限土下路堤頂面回彈模量（以下簡稱模量）較低，需在其上部進行剛度補償[1]，以達到路基頂面設計模量和驗收彎沉值的要求。高液限土下路堤頂面模量的快速準確測定對于高液限土路基施工質量控制和剛度補償設計至關重要。

現場測定路基模量的方法主要有承載板法、貝克曼梁法、落錘彎沉儀FWD法和便攜式落錘彎沉儀PFWD法等。承載板法和貝克曼梁法耗時費力，所需測試人員多;FWD需專用車牽引，偏僻地方不宜到達，這3種方法多用于成型路基，難以用于路基施工質量控制[2]，雖然PFWD測試簡便，但以往反算模量時僅取實測荷載和位移時程曲線的峰值，并假設路基為線彈性體，忽略了其他的時程數據和荷載位移的非線性[3-5]。對于沖擊荷載作用下變形響應滯后且荷載位移非線性顯著的路基，基于線彈性模型和靜力分析方法反算的模量（簡稱常規反算模量）與承載板法直接實測的靜模量（簡稱實測模量）相差較大[6]。有學者通過現場試驗，建立了常規反算模量和實測模量的回歸關系[7-8]，但現場檢測工作量大，適用范圍有限。學者們曾對FWD和PFWD沖擊荷載作用下路基、路面非線性動力響應開展研究，有學者將變形滯后歸因于彈性波傳遞時間，基于彈性動力學改進了常規反算方法，但僅將反算結果與基于線彈性模型的反算模量進行了對比[9-11]。也有學者將變形滯后歸因于材料的粘彈性，基于粘彈性理論，改進了反算方法[12-18]，并提高了模量反算精度[19-23]，但主要針對路面多層模量反算，且多采用多參數復雜理論模型，若用于高液限土路基模量反算，將增加計算難度，也可能導致結果不收斂。

為解決PFWD常規反算中因理論假設與實際情況不符導致的反算高液限土路基模量與實測模量相差較大的問題，筆者基于粘彈性模型，采用準靜態動力響應分析方法，提出并驗證了既能反映高液限土路基非線性動力響應特征，又能用動載數據反算靜力參數的高液限土路基模量反算新方法，編制了相應的反算程序。同時，將其應用于路基施工質量控制與剛度補償設計。

1 高液限土路基模量現場試驗

海南萬寧至洋浦高速公路橫貫海南島，全長163 km，沿線開挖并用于路基填筑的高液限土約240萬m3。在高液限土填方量較大的第六、第九和第十合同段，分別選取K67+190～K67+290 （WY-6）、K110+180～K110+280 （WY-9）和K121+460～K121+560 （WY-10）作為試驗段。對試驗段填料進行基本性質指標測試，結果如表1所示。由于高液限土天然含水率均遠大于其最佳含水率，在海南多雨氣候條件下，很難通過翻曬將高液限土填料含水率大幅降至最佳含水率壓實。因此，在滿足下路堤填料強度和變形要求前提下，在3個試驗段均只將高液限土直接用作下路堤填料，在大于最佳含水率8%～10%狀態下壓實，并適當降低壓實度控制標準[24]。

利用高液限土填筑下路堤后，分別在3個試驗段下路堤頂面沿縱向每10 m一個測點，依次進行PFWD檢測和承載板試驗。使用的PFWD設備主要參數為：載荷板半徑0.15 m，載荷范圍1～15 kN，載荷脈沖形狀為半正弦波;載荷傳感器相對誤差小于1%，絕對誤差±0.1 kN;位移傳感器有效測試精度1 μm，最大測試范圍2 200 μm;數據采集周期0～60 ms。PFWD測試方法和步驟參照文獻[2]進行。現場承載板試驗參照《公路路基路面現場測試規程》（JTG E 60—2008）相關規定進行。

限于篇幅，僅列出3個試驗段部分代表性PFWD試驗結果，如圖1所示。從圖1（a）～（c）可以看出，3個測點PFWD荷載與豎向位移時程曲線均有相似性，當施加的荷載達到峰值時，該時刻對應的豎向位移并未達到峰值，變形未達到最大;當位移達到峰值時，荷載已處于減小階段。從圖1（d）可以看出，3個測點的荷載位移曲線表現出明顯的非線性和滯回圈。因此，沖擊荷載作用下高液限土填筑層變形滯后效應顯著。

PFWD常規模量反算法是假設荷載與變形關系近似為線彈性，與承載板法一樣，均采用圓形垂直剛性分布靜荷載作用下的彈性半空間布辛尼斯克解（見式（1））計算路基模量。

E=πR2p（1-μ2）w（1）

式中：E為路基模量值，MPa;p為載荷板壓力峰值，MPa;R為載荷板半徑，m;μ為泊松比，取0.35;w為載荷板中心彎沉峰值，mm;π為圓周率。

由于沖擊動荷載作用下變形存在滯后，且線彈性靜力模型無法反映高液限土路基的非線性動力響應特征，若仍采用式（1）反算模量會造成結果的偏差。現場試驗結果表明，圖1（a）～（c）3個測點的常規反算模量分別為27.6、24.4、31.5 MPa，而實測模量分別為18.5、15.1、21.2 MPa。3個試驗段30個測點的常規反算模量與實測模量如圖2所示，統計的常規反算模量平均絕對誤差10.9 MPa，平均相對誤差52.5%。

2 基于粘彈性模型的模量反算方法

由于以往PFWD反算路基模量時采用的是線彈性靜力學模型，而沖擊荷載作用下高液限土路基具有顯著變形滯后效應和荷載位移非線性特征，常規反算方法已不適用，因此，有必要建立一種可較好地反映沖擊荷載作用下高液限土路基非線性動力響應特征的簡便模量反算方法。

2.1 選用的粘彈性理論模型

眾所周知，在正弦周期動荷載作用下，粘彈性材料的應變也呈周期變化，而且應變響應滯后于應力響應。粘彈性理論模型也普遍應用于行車荷載作用下瀝青路面動力響應分析。考慮到沖擊荷載作用下高液限土路基變形滯后效應與上述粘彈性材料力學行為相似，因此，基于粘彈性本構模型建立了高液限土模量反算新方法。

粘彈性模型中，Maxwell模型是由彈簧阻尼器串聯而成，主要用于模擬粘彈性材料應力松弛過程。三參量固體模型、Burgers模型和廣義Maxwell模型等是用彈簧阻尼器并聯和串聯多種形式構造出的更加復雜的力學模型，可以描述動荷載作用下材料的粘彈性以及殘余變形性質。而PFWD測試時，會通過多次落錘消除測點的塑性變形，因此，反算高液限土路基模量不需考慮殘余變形，不必采用形式復雜的多參數粘彈性模型增加反算難度。

Kelvin模型是由彈簧阻尼器并聯構成的粘彈性模型[11]。該模型形式簡潔，便于高效地迭代運算。其數學描述見式（2）。

根據式（3）可得到加卸載作用下的應力應變曲線，如圖3所示。由圖3可以看出，當引入粘滯系數后，加載時應力首先增至最大值，應變隨后增至最大值，應變具有滯后性，應力應變曲線形式與圖1（d）所示的PFWD實測荷載位移曲線形式極為相似。因此，選用Kelvin模型用于沖擊荷載作用下高液限土路基動力響應分析。

2.2 準靜態反算方法

動態法和準靜態法[15，26]是動荷載作用下彈性體系動力響應分析的兩種方法。

動態法反算[27]是將Navier動力方程中引入粘彈性理論模型，通過Laplace和Hankel反算導出豎向位移的顯式解，并考慮復雜混合邊值問題反算模量。由于反算時隱式偏微分方程結構較復雜，需采用諸多簡化數值算法進行，比較耗時。

采用準靜態法反算思路是將靜荷載作用下彈性半空間體表面的豎向位移顯式解作Laplace變換，并將變換式中的彈性參數代之以粘彈性算子再作反算。這種方法可用動載數據反算靜力參數。后續的結果也驗證了對于高液限土路基采用準靜態法進行反算，其結果精度能夠滿足要求。因此，采用該方法和PFWD動載數據反算的模量屬于靜模量，從而與承載板法測得的靜模量在類型上保持一致。

式中：w（r，t）為PFWD剛性載荷板作用下粘彈性半空間體表面豎向位移，mm;L-1（w-（r，s））為豎向位移的拉普拉斯反變換;E（s）=E+ηs為粘彈性算子，η為粘滯系數;E和μ的意義同式（1）;F為PFWD落錘時作用于測點表面的集中力，kN，由荷載時程曲線得到;R和r的意義同式（4）;s為時間t的Laplace變換參量。

由式（5）可知，當t=0時，豎向位移為0;當t趨近于無窮時，豎向位移等于傳統彈性半空間理論計算得到的豎向位移。粘滯系數η所在的項，隨著時間的變化是一個始終大于0小于1的數，限制了整體豎向變形，使理論計算位移時程的峰值縮小和相位向右延展。

2.3 模量反算程序的編制

由式（5）的形式可知，反算參數為模量值E和粘滯系數η。因式（5）比較復雜，難以得到反算參數的解析解，故采用最小二乘法，即式（6）迭代求極值的優化算法進行反算。

由于基于最小二乘優化算法得到的是采用函數定義域內全局求極值的反算結果，該反算結果可能與實際情況相差較大，因此，在編制反算程序時，針對PFWD檢測高液限土路基模量的具體情況作了如下處理：由于數據采集周期0～60 ms內落錘會在橡膠塊上振動，進而帶動承載板產生小幅跳動，故只取0～25 ms內峰值波形的數據;計算點位r=0 m，即荷載作用面表面的中心處;精度控制參數K=0.5和迭代控制系數ε=0.01，兩個控制值可按照不同精度要求進行調整。

進行反算時還需要將式（8）進行變形得到式（11），以控制反算模量值的權重。當計算位移時程的相位大于實測位移時程或計算位移峰值小于實測值，但迭代還未滿足式（9）的要求時，停止參數η的迭代，而繼續進行參數E的迭代。

按照上述方法，利用Matlab編寫了考慮沖擊荷載作用下變形滯回效應的高液限土路基模量反算程序[28]，既適用于FWD反算，也適用于PFWD反算。反算流程如圖4所示。

3 模量反算新方法的驗證與應用

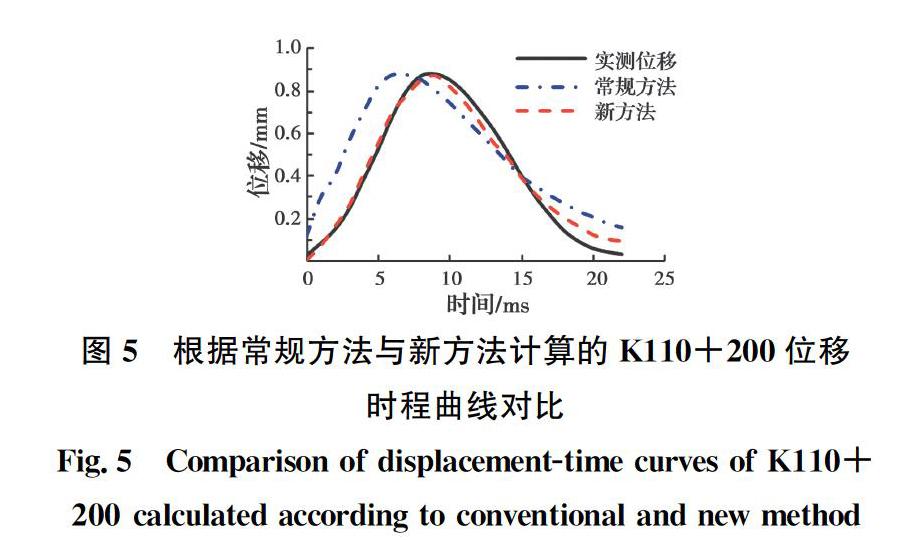
根據圖1所示3個測點的PFWD荷載和位移時程曲線，利用本文提出的基于粘彈性模型的高液限土路基模量反算方法（簡稱新方法）進行了模量反算，并與常規方法的反算結果和實測結果進行了對比，如表2所示。3個測點的反算結果表明，新方法反算的模量僅比相應的實測模量大2 MPa左右，而常規反算模量比實測模量要大10 MPa左右，新方法的模量反算精度提高了40%左右。

分別利用新方法和常規方法反算得到的模量正算位移時程，并與實測位移時程進行對比。其中，圖5為測點K110+200位移時程曲線對比結果。由圖5可以看出，基于粘彈性模型的新方法計算得到的位移時程與實測位移時程非常吻合。根據式（13），新方法的計算精度系數則為0.935，常規方法得到的精度系數僅為0.693。K110+200和K121+500精度系數對比結果相似，一同列于表2。以上位移時程與精度系數對比結果表明，引入粘彈性模型后，新方法能較為準確地反映沖擊荷載作用下高液限土路基變形響應滯后這一特征。

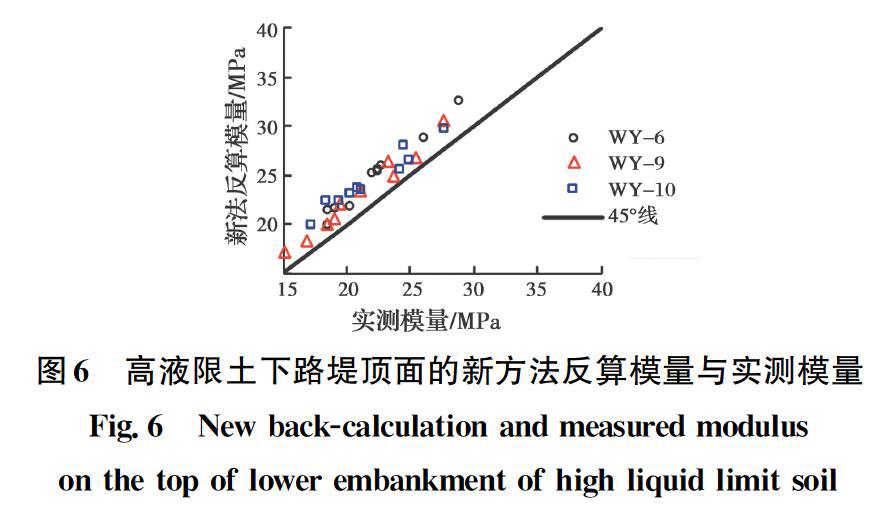
按照新方法對3個試驗段30個測點進行模量反算的結果如圖6所示。對比圖2可看出，新方法反算模量相對常規反算模量更接近實測模量，平均絕對誤差僅為2.6 MPa，平均相對誤差為9.2%。同時也證明了，由于采用了準靜態分析方法，可根據沖擊荷載作用下路基動力響應（荷載和位移時程數據）反算靜力參數，從而使得新方法反算模量更接近由承載板法實測的靜模量。

良好的路基施工質量必然要求在各層位施工完成后路基強度變異性小，均勻一致[29]。為此，應用PFWD和模量反算新方法，對海南萬洋高速公路高液限土下路堤頂面模量的變異性進行了評價，快速、準確地確定了模量過低需要補壓處理的點位，減小了下路堤模量的變異性。由于高液限土下路堤模量較低，而萬洋高速公路路基頂面設計彎沉值為120（0.01 mm），需要在上路堤和路床填筑合適填料進行剛度補償。為此，采用文獻[2]的方法，繼續以WY-9為試驗段，進行了路基剛度補償設計和現場試驗，確定并實施了用高液限土摻30%砂礫填上路堤，用高液限土摻40%砂礫填下路床，用低液限土摻4%水泥填上路床方案。實測路基彎沉的代表值為88（0.01 mm），滿足驗收要求。

為研究新方法對于高模量路基測試的適用性，在WY-9試驗段路基頂面分別進行了PFWD與承載板試驗。其中，K110+200處PFWD測試結果如圖7所示。與圖1（b）、（d）相比，由于路基模量提升，沖擊荷載作用下變形滯后效應和荷載位移滯回圈雖顯著減小，但仍然存在，同樣會導致常規反算誤差。承載板實測與PFWD模量反算結果表明：實測模量為196.1 MPa，常規反算模量為221.10 MPa，新方法反算模量為205.6 MPa。

圖8為WY-9試驗段路基頂面所有10個測點的模量實測與反算結果。統計結果表明：新方法反算模量平均絕對誤差為8.5 MPa，平均相對誤差僅為4.3%;而常規反算模量平均絕對誤差為24.1 MPa，平均相對誤差為12.2%。可以看出，當路基模量較高時，新方法和常規方法反算模量的平均相對誤差均有所減小，但新方法反算結果的精度更高。

根據高液限土路基試驗段現場試驗結果，由于在低模量的下路堤和高模量的路床頂面新方法反算模量與實測模量之間的相對誤差均在10%以內，因此，可將新方法反算的模量直接作為高液限土路基剛度補償設計的參數。

4 結論

1）沖擊荷載作用下高液限土路基變形峰值滯后于荷載峰值，荷載位移曲線彈性滯回明顯。

2）基于線彈性靜力模型的PFWD模量常規反算方法忽略了路基非線性動力響應特征，用于高液限土路基模量測定時，反算模量與實測模量偏差較大。

3）基于粘彈性模型和準靜態法的PFWD模量反算新方法既可反映路基非線性動力響應特征，又可用動載數據反算靜模量;在下路堤和路床頂面，采用新方法反算的模量均與實測模量接近，誤差在10%以內。

4）模量反算新方法可用高液限土路基各層位頂面模量變異性控制，建議將新方法反算模量作為路基剛度補償的設計參數。

參考文獻：

[1] 鄭健龍， 張銳. 公路膨脹土路基變形預測與控制方法[J]. 中國公路學報， 2015， 28（3）： 1-10.

ZHENG J L， ZHANG R. Prediction and control method for deformation of highway expansive soil subgrade [J]. China Journal of Highway and Transport， 2015， 28（3）： 1-10. （in Chinese）

[2] 查旭東. PFWD快速檢測路基模量研究[J]. 公路交通科技， 2009， 26（1）： 26-30.

ZHA X D. Study of rapid test of subgrade modulus with PFWD [J]. Journal of Highway and Transportation Research and Development， 2009， 26（1）： 26-30. （in Chinese）

[3] NAZZAL M D， MOHAMMAD L N. Estimation of resilient modulus of subgrade soils using falling weight deflectometer [J]. Transportation Research Record， 2010， 2186（1）： 1-10.

[4] PIERCE L M， SMITH K D， BRUINSMA J E， et al. Case studies using falling weight deflectometer data with mechanistic-empirical design and analysis[M]// Pavement Performance： Current Trends， Advances， and Challenges. 100 Barr Harbor Drive， PO Box C700， West Conshohocken， PA 19428-2959： ASTM International， 2012： 1-14.

[5] 張軍輝， 彭俊輝， 鄭健龍. 路基土動態回彈模量預估進展與展望[J]. 中國公路學報， 2020， 33（1）： 1-13.

ZHANG J H， PENG J H， ZHENG J L. Progress and prospect of the prediction model of the resilient modulus of subgrade soils [J]. China Journal of Highway and Transport， 2020， 33（1）： 1-13. （in Chinese）

[6] 梁新政， 王復明， 孔憲京. 路基模量反演結果分析[J]. 巖土工程學報， 2000， 22（5）： 619-621.

LIANG X Z， WANG F M， KONG X J. Analysis for result of subgrade modulus backcalculation [J]. Chinese Journal of Geotechnical Engineering， 2000， 22（5）： 619-621. （in Chinese）

[7] 段丹軍， 查旭東， 張起森. 應用便攜式落錘彎沉儀測定路基回彈模量[J]. 交通運輸工程學報， 2004， 4（4）： 10-12.

DUAN D J， ZHA X D， ZHANG Q S. Subgrade resilience modulus measuring by portable falling weight deflectometer（PFWD） [J]. Journal of Traffic and Transportation Engineering， 2004， 4（4）： 10-12. （in Chinese）

[8] 楊博， 張銳， 查旭東， 等. 一種路基動模量測試方法[J]. 巖土力學， 2014， 35（5）： 1514-1519.

YANG B， ZHANG R， ZHA X D， et al. A method for testing dynamic mouduli of subgrade [J]. Rock and Soil Mechanics， 2014， 35（5）： 1514-1519. （in Chinese）

[9] 查旭東， 袁盛杰， 肖秋明. 沖擊荷載作用下的路基動力反算[J]. 長沙理工大學學報， 2014， 11（4）： 1-7， 14.

ZHA X D， YUAN S J， XIAO Q M. Subgrade dynamic backcalculation under impact loading [J]. Journal of Changsha University of Science & Technology， 2014， 11（4）： 1-7， 14. （in Chinese）

[10] LIU X L， ZHANG X M， WANG H， et al. Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors [J]. Construction and Building Materials， 2019， 195： 178-186.

[11] HAMIM A， YUSOFF N I M， CEYLAN H， et al. Comparative study on using static and dynamic finite element models to develop FWD measurement on flexible pavement structures [J]. Construction and Building Materials， 2018， 176： 583-592.

[12] LI M Y， WANG H. Prediction of asphalt pavement responses from FWD surface deflections using soft computing methods [J]. Journal of Transportation Engineering， Part B： Pavements， 2018， 144（2）： 04018014.

[13] LI M Y， WANG H， XU G J， et al. Finite element modeling and parametric analysis of viscoelastic and nonlinear pavement responses under dynamic FWD loading [J]. Construction and Building Materials， 2017， 141（1）： 23-35.

[14] ZHANG J H， PENG J H， LIU W Z， et al. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction [J]. Road Materials and Pavement Design， 2019， 2019（1）： 1-13.

[15] 鄭傳超. 道路結構力學計算[M]. 北京： 人民交通出版社， 2003.

ZHENG C C. Mechanical calculation of road structure [M]. Beijing： China Communications Press， 2003. （in Chinese）

[16] 曹丹丹， 趙延慶， 田澤峰， 等. 瀝青路面動態黏彈反演研究[J]. 土木工程學報， 2017， 50（9）： 104-109.

CAO D D， ZHAO Y Q， TIAN Z F， et al. Back-calculation study on asphalt pavement using dynamic viscoelastic method [J]. China Civil Engineering Journal， 2017， 50（9）： 104-109. （in Chinese）

[17] GRASMICK J G， MOONEY M A， SENSENEY C T， et al. Comparison of multiple sensor deflection data from lightweight and falling weight deflectometer tests on layered soil [J]. Geotechnical Testing Journal， 2015， 38（6）： 20140172.

[18] SIRITHEPMONTREE H， SAPSATHIARN Y. Dynamic soil models for backcalculation of material properties from falling weight deflectometer deflection data [J]. Procedia Engineering， 2017， 189： 152-157.

[19] ZHANG J H， GU F， ZHANG Y Q. Use of building-related construction and demolition wastes in highway embankment： Laboratory and field evaluations [J]. Journal of Cleaner Production， 2019， 230： 1051-1060.

[20] ASLI C， FENG Z Q， PORCHER G， et al. Back-calculation of elastic modulus of soil and subgrade from portable falling weight deflectometer measurements [J]. Engineering Structures， 2012， 34： 1-7.

[21] BENEDETTO A， TOSTI F， DI DOMENICO L. Elliptic model for prediction of deflections induced by a Light Falling Weight Deflectometer [J]. Journal of Terramechanics， 2012， 49（1）： 1-12.

[22] NEGA A， NIKRAZ H， AL-QADI I L. Dynamic analysis of falling weight deflectometer [J]. Journal of Traffic and Transportation Engineering （English Edition）， 2016， 3（5）： 427-437.

[23] ZHANG J H， PENG J H， ZENG L， et al. Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties [J]. International Journal of Pavement Engineering， 2019（1）： 1-8.

[24] 張銳， 肖宇鵬， 劉闖， 等. 考慮吸附結合水影響的高液限土路基壓實度控制標準[J]. 中國公路學報， 2020， 33（1）： 32-40， 50.

ZHANG R， XIAO Y P， LIU C， et al. Control standards for degree of compaction of high liquid limit soil subgrade considering effects of adsorbed bound water [J]. China Journal of Highway and Transport， 2020， 33（1）： 32-40， 50. （in Chinese）

[25] 謝定義. 土動力學[M]. 北京： 高等教育出版社， 2011.

XIE D Y. Soil dynamics[M]. Beijing： Higher Education Press， 2011.（in Chinese）

[26] 郭大智， 任瑞波. 層狀粘彈性體系力學[M]. 哈爾濱： 哈爾濱工業大學出版社， 2001.

GUO D Z， REN R B. Layered viscoelastic system mechanics [M]. Harbin： Harbin Institute of Technology Press， 2001.（in Chinese）

[27] 楊博， 鄭健龍， 查旭東. 剛柔復合式路面動測評價方法與試驗研究[J]. 中國公路學報， 2015， 28（5）： 77-86.

YANG B， ZHENG J L， ZHA X D. Dynamic testing evaluation method and experimental research for rigid-flexible composite pavement [J]. China Journal of Highway and Transport， 2015， 28（5）： 77-86. （in Chinese）

[28] 張銳， 滕煜晟， 劉闖， 等. 基于FWD的細粒土路基模量反算軟件[CP]. 2018.

ZHANG R， TENG Y S， LIU C， et al. Software for calculating modulus of fine soil subgrade based on FWD [CP]. 2018.（in Chinese）

[29] 李躍軍， 吳亞中， 李亮. 基于可靠度的路基均勻性評價標準[J]. 交通運輸工程學報， 2010， 10（3）： 17-22.

LI Y J， WU Y Z， LI L. Uniformity evaluation standard of subgrade based on reliability [J]. Journal of Traffic and Transportation Engineering， 2010， 10（3）： 17-22. （in Chinese）

（編輯 王秀玲）